基于改进广义cat映射的彩色卫星图像加密算法

张新，柏逢明

（长春理工大学 电子信息工程学院，长春 130022）

随着信息技术的发展，保护图像的安全显得越来越重要，尤其是军事或商业卫星图像涉及国家机密、军事安全和公司利益等，因此要保证在存储和传输过程中图像的安全。混沌系统具有对初始条件的极端敏感性和非周期性，可以很好的运用于图像加密。近年来，许多学者利用混沌系统对图像加密进行了大量的研究。Chen等［1］提出利用二维广义Arnold变换构造三维Arnold变换。王猛［2］提出了一种基于maker map混沌理论的卫星图像加密技术，但是安全性不高，密钥直接设定容易被破解。吴成茂［3］提出一种离散Arnold变换改进及其在图像置乱加密中的应用，取得了良好的加密效果，但是只是基于离散二维Arnold映射改进进行了实验结果和分析。本文提出了一种基于改进广义cat映射的彩色卫星图像加密算法。通过理论分析和仿真实验检测，结果能够达到相应的安全水平。

1 基本理论

1.1 复合混沌映射CCM［4］（compound chaos mapping）

标准帐篷映射的方程为：

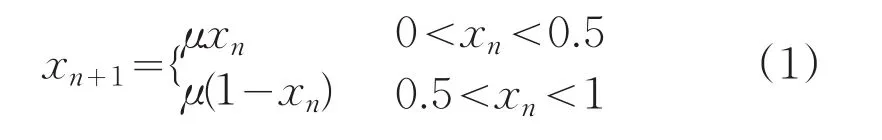
研究表明，当 μ＞1时，方程（1）表现为混沌状态，并且混沌带随着μ增大而逐渐扩大。

Logistics混沌映射为：

当3.5699456＜λ≤4时，Logistics映射处于混沌状态。当λ=4时，在(0,1)上达到满映射。因此当取值 λ=4时，式（2）变为：

由于式（1）中xn的值始终处在(0,1)之间，即无论对（1）式怎样取值，其值域都不会超出式（3）的定义域范围，因此，将式（1）代入到（3）中，便得到新的复合混沌映射，称其为CCM：

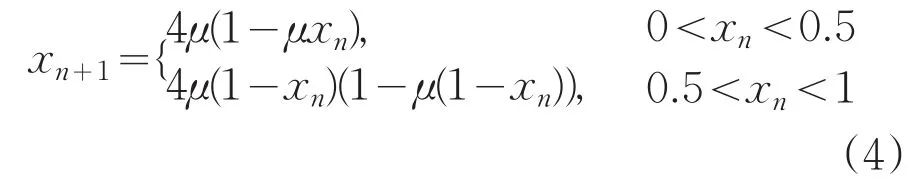
复合混沌映射的分插图如图1，可见当μ∈(0.4,2)时，该系统处于一种混沌态。

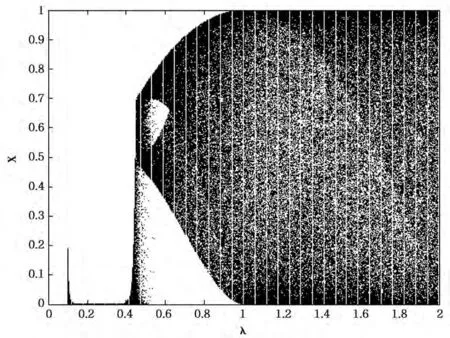
图1 CCM分叉图

1.2 改进的广义cat映射

为了提高图像的置乱效果，下面对广义cat映射进行了改进。

广义Arnold映射的方程定义为：

其中det(A)=1；a,b以 N为周期，故要求a,b∈N。

将式（5）的方程组形式改写为：

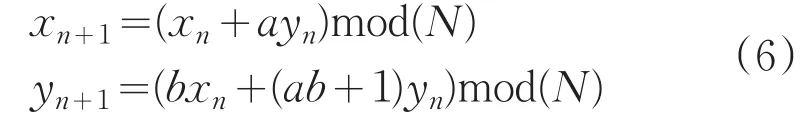
针对式（6），将其改进表达式为：

其中 f(xn+1)=x2n+1。

对于式（7），其可逆映射表达式为：

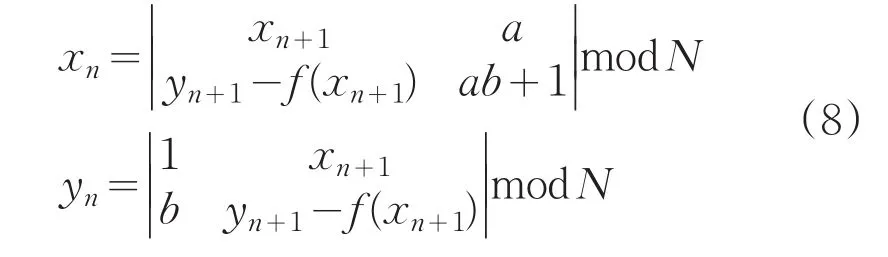
根据有限整数域上的可逆变换一定存在变换周期的判定定理，可得知式（8）仍是一种具有周期的可逆一一映射，可以利用其逆映射或者是其周期性便能恢复置乱前原图像。

2 彩色卫星图像加密算法

本文提出的加密算法是一种改进广义cat映射的加密算法。在置乱阶段，应用改进的广义cat映射以不同的参数和迭代次数对原始图像的三个色彩分量进行三轮置乱。在扩散阶段，由CCM复合混沌映射对置乱图像进行扩散。加密流程图如图2所示。

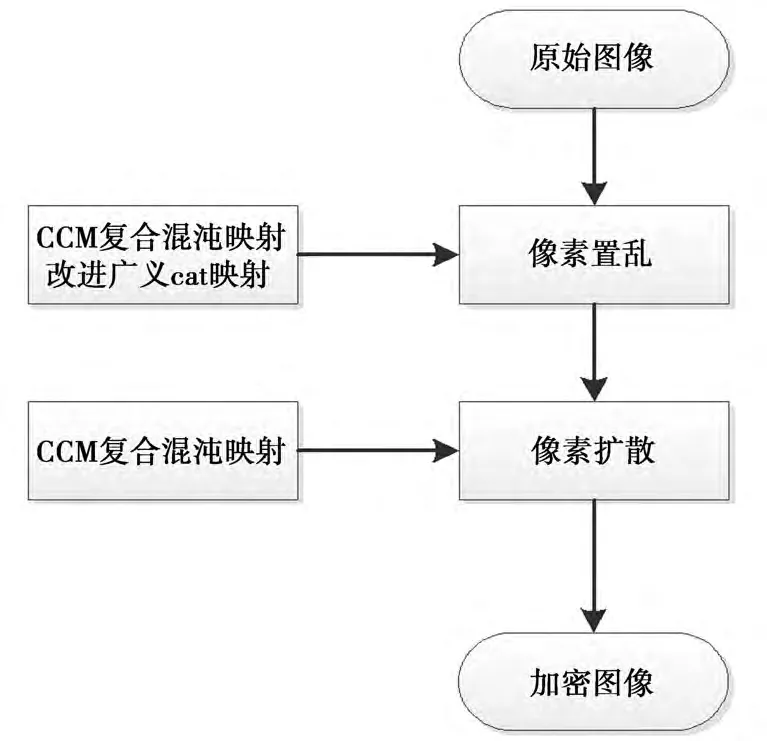
图2 加密流程图

原始图像I是N×N×3大小的彩色卫星图像，CCM映射的初始条件x1(0)，x2(0)和x3(0)，控制参数m1，m2和m3以及M作为部分加密密钥。

当初始条件为x1(0)和控制参数为m1，迭代CCM产生一个序列I1(n)，取序列的第M 个值，得到x1(M)；同样的方法，当初始条件为x2(0)和控制参数为m2，迭代CCM产生一个序列I2(n)，取序列的第M个值，得到x2(M)；当初始条件为x3(0)和控制参数为m3，迭代CCM产生一个序列I3(n)，取序列的第 M 个值，得到 x3(M)。 x1(M)，x2(M)，x3(M)和I1(n)，I3(n)，I3(n)分别用于置乱阶段和扩散阶段。

在置乱阶段使用改进后的广义cat映射，如式（9）所示：

图3 “长春理工大学”彩色原始图像（a），加密图像（b）和解密图像（c）

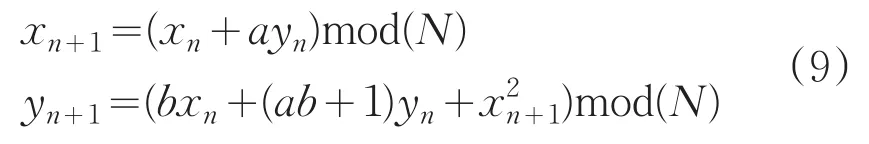
控制参数a，b如下式描述：

根据（9）式，对原始图像三个色彩分量RGB分别进行三轮置乱，得到置乱图像CR，CG，CB。

在扩散阶段，由CCM映射产生的I1(n)，I2(n)，I3(n)，对此三个序列分别进行隔d个点抽样成有N×N 个序列值的序列Y1(n)，Y2(n)，Y3(n)，如式（11）所示：

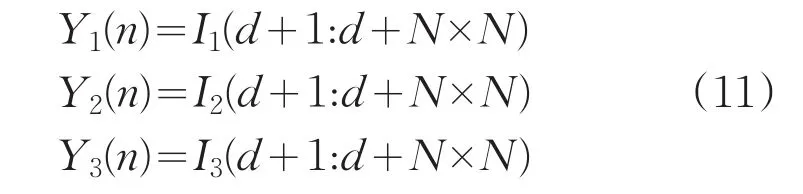
其中，Yj(n)的序列长度为N×N，d为正整数。因为图像的大小为N×N，所以CCM所产生的三个Ij(n)的序列长度L≥N×N，j=1,2,3。

扩散密钥流Kj由（12）式方法生成：

这里，i=1,2,3,...,ceil(N×N)，j=1,2,3。

将密钥流Kj(i)从上到下，从左到依次进行排列将其转化为三个N×N的矩阵：X1，X2，X3。

置乱图像通过Xj矩阵进行扩散加密，得到密文矩阵：

然后将此处的SR，SG和SB这三个矩阵进行色彩合成既得到加密图像。

解密图像就是对加密算法进行逆运算。

3 实验性能分析

3.1 直方图分析

在MATLAB 2010系统条件下，采用256×256像素的“长春理工大学”彩色卫星图像作为明文图像，CCM映射的初始值和控制参数分别为：x1(0)=0.2899，m1=1.6；x2(0)=0.5193，m2=1.4；x3(3)=0.0048，m3=0.8；M=300；d=1000。原始图像、加密图像、解密图像由图3给出，其三个RGB色彩分量像素直方图由图4给出。如图4可见，加密图像的直方图均匀分布，具有很好的统计特性，可以抵抗统计攻击。

图4 “长春理工大学”原始图像（a），加密图像（b）和解密图像（c）的RGB三个色彩分量直方图

3.2 密钥空间

本文的加密算法采用了复合混沌映射，其三对初始值和控制参数作为密钥，则其组成的密钥空间至少为1042；密钥M以及抽样隔点d都可以增大密钥空间。加密图像专家建议密钥空间大于264可以抵抗暴力破解，因此该加密算法足够安全。

3.3 密钥敏感性分析

为了验证该算法的敏感性，在保持其他密钥值不变的前提下，现对解密密钥做如下改动：将CCM映射的初始值密钥x1(0)改为0.2898，得到的解密图像如图5（a）；将CCM映射的控制参数m1改为1.5，得到的解密图像如图5（b）；将 M 改为299，得到的解密图像如图5（c）。

图5 错误解密结果

由图5可知，即使是对密钥做微小的改变，解密图像也是错误的，满足了雪崩效应，因此该算法具有很强的密钥敏感性。

3.4 信息熵分析

对加密图像的RGB三个分量进行信息熵分析，通过MATLAB系统计算，“长春理工大学”彩色卫星图的三个色彩分量的信息熵分别为：HR(m)=7.9895，HG(m)=7.9898，HB=7.9900，非常接近理想值8。由此可见，加密图像的信息熵足够大，可以有效地抵抗熵攻击。

3.5 像素相关性分析

随机选取原始图像和加密图像的1000对水平相邻像素、垂直相邻像素、以及对角相邻像素的相关性，由图6所示。

图6 “长春理工大学”彩色卫星图像的相关性

其中，（a）原始图像水平方向相邻像素；（b）加密图像水平方向相邻像素；（c）原始图像垂直方向相邻像素；（d）加密图像垂直方向相邻像素；（e）原始图像对角方向相邻像素；（f）加密图像对角方向相邻像素。由此可见，加密后图像像素相关性小，可以有效抵抗统计攻击的能力。

4 结论

经过实验分析与仿真结果可知应用复合混沌映射和和改进后的cat映射对图像进行加密保证了该算法的复杂性的大大提高了图像加密的效果。加密后像素分布均匀、相邻像素点相关性很弱，具有抵抗统计攻击能力强、有效抵抗熵攻击、密钥敏感性强等特点，算法安全性较高。将此方法运用到卫星图像加密中可以取得很好的效果。但是卫星测绘不断的发展，如何实现卫星图像的实时性要求、保证传输的安全性等非常值得研究。

［1］Chen Guanrong，Mao Yaobin，Charles K Chui.A symmetric image encryption scheme based on 3D chaotic cat maps［J］.Chaos Solution and Fractals，2004（21）：749-761.

［2］王猛.提出了一种基于maker map混沌理论的卫星图像加密技术研究［D］.哈尔滨：哈尔滨工业大学，2008.

［3］吴成茂.离散Arnold变换改进及其在图像置乱加密中的应用［J］.物理学报：2014，63（9）：090504-1-090504-20.

［4］李锦青，柏逢明，底小强.基于Hopfield混沌神经网络的彩色图像加密算法研究［J］.长春理工大学学报：自然科学版，2012，35（4）：117-121.

［5］赵希奇，柏逢明，吕贵花.基于混沌理论和Hash函数的自适应图像加密算法［J］.长春理工大学学报：自然科学版，2014，37（4）：117-120.

［6］张雪峰，范九伦.一种新的分段非线性映射及其性能分析［J］.物理学报，2010，59（4）：2298-2304.