复杂网络松耦合分布式计算框架的设计与实现
卢 罡,徐勤良,许南山,郭俊霞
(北京化工大学信息科学与技术学院,北京100029)
复杂网络松耦合分布式计算框架的设计与实现
卢 罡,徐勤良,许南山,郭俊霞
(北京化工大学信息科学与技术学院,北京100029)
为更快地计算大尺度复杂网络结构的相关参数,设计并实现一种松耦合分布式计算框架。将分散于网络中的松耦合计算节点汇集起来,通过任务队列使各计算节点共同参与复杂网络的相关分布式计算,并能随时加入或者退出计算,利用分散于网络中松耦合的计算节点提高复杂网络相关分析的计算速度。基于该框架,实现对大尺度复杂网络的平均最短路径长度、网络直径和网络效率的分布式计算。实验结果表明,在保证计算结果正确的前提下,该框架可充分利用网络中闲散的计算资源,提高运算效率。
复杂网络;分布式计算;因特网通信引擎;松耦合;M/S模式
1 概述
近年来,复杂网络在各个领域的应用越来越广泛,人们频繁利用网络科学的概念及方法思考和解决各领域的相关科学问题。而随着所研究网络的规模越来越大,针对大尺度网络分析的图计算、图挖掘问题也日显突出。2013年在杭州举行的“大数据时代下复杂网络的机遇与挑战”研讨会中提出了目前复杂网络研究面临的最主要的10个挑战,其中就有在大数据的背景下如何快速准确地处理包含数千万甚至数亿节点大尺度网络的问题[1]。
随着多核计算技术、Hadoop技术、GPGPU技术的发展,基于这些技术的大尺度网络的并行分析与计算研究也正广泛地开展。比如基于多核CPU[2-4]、GPU[5-6]以及异构系统[7-8]上的最短路径、节点介数的计算[9]。卡内基梅隆大学开发的GraphChi框架[10]以及后续的GraphCT框架[11]通过精心设计的存储结构和算法,充分利用了单机的并行计算资源。此外,卡耐基梅隆大学开发的Pegasus[12]以及最近研发的HADI[13],均是基于Hadoop平台的图算法引擎。但基于Hadoop的实现要求基于高速网络对可用的集群环境先做好规划,而且一旦计算开始,不易动态调整计算节点的负载和数量。而建立松耦合计算网络框架,将网络中闲置的各种不同的操作系统下和不同配置的计算机联合起来,共同处理复杂网络的相关分布式计算,可以大大提高计算效率。参与者可以随时加入或退出计算,并随时动态调整负载,从而将散落于网络中的计算资源低成本、灵活动态地利用起来,节省了管理服务器集群的成本。这种机制称为“志愿计算”,最早由加州伯克利大学的BOINC[14-15]项目提出。BOINC是目前最著名、使用最广泛的志愿计算平台,并且在平台上活跃着近百个分布式计算项目,涵盖了多个科学领域,但是还未见有复杂网络分析、模拟方面的项目,并且BOINC框架式通过设定为每个计算节点的任务预期完成时间来进行容错处理,但是复杂网络的计算由于计算时间同网络规模有关,所以不能很好地预测任务完成时间,BOINC的结果验证机制是通过分配相同任务给不同的计算节点比较最终结果。
由于复杂网络的相关分析与计算以节点或边为中心,因此可以由与节点或边相关的计算构成任务队列。这种基于任务队列的架构有利于负载均衡和容错机制的实现。本文基于该任务队列的计算模式以及志愿计算的基本思想,设计针对大尺度复杂网络分析计算的松耦合分布式计算框架,并基于该框架实现大尺度复杂网络的平均最短路径长度、网络直径和网络效率[16]的分布式计算。由ZeroC开发的中间件因特网通信引擎(Internet Communica-tions Engine,ICE)具有通信负载低、与平台和语言无关等优点[17-18],因此在计算框架的具体实现上,本文采用ICE作为网络通信中间件,通过局域网或者互联网将松耦合的计算节点以M aster-Slave模式共同参与复杂网络的相关分布式计算。
2 复杂网络的松耦合分布式计算框架
本文提出的针对大尺度网络的松耦合分布式计算框架与BOINC不同,主要针对复杂网络的计算特点进行设计,采用心跳信号的机制进行错误判断而不是通过预判时间,旨在将框架抽取通用接口,将其用到复杂网络的其他计算中。本文框架采用通用的M aster-Slave模式,不同配置的Slave节点都可以通过局域网或广域网与M aster节点通信,共同完成计算任务。
本文框架的主要设计思想为:外部应用程序接收计算需求,M aster节点将任务均匀的分成若干个任务集,Slave节点申请加入计算,由M aster节点根据其系统配置动态分配不同个数任务集交由相应的Slave节点计算,Slave节点计算完成后回传计算结果,最终由M aster节点进行运算结果汇总统计。基于任务队列的分布式计算框架的架构如图1所示。该框架至少需要一个M aster节点和Slave节点,理论上可同时存在成百上千个Slave节点参与计算,实际最大可运行数量取决于M aster节点性能,任务队列管理性能以及网络通信速率等指标来决定。
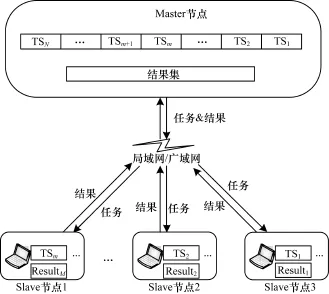
图1 基于任务队列的分布式计算框架
2.1 M aster节点
M aster节点是本文分布式框架的核心,主要任务包括:分解任务并维护任务队列,接收Slave节点的计算请求,实时监控Slave节点的运行状态,实时监控任务运行状态,为Slave节点分配计算任务,接收子任务计算结果,汇总全部子任务结果集。
根据不同的算法,大尺度复杂网络的节点或边被组织成计算任务队列。M aster节点负责根据需要将任务队列分割为细粒度的任务集分配给申请参与运算的Slave节点。M aster节点通过维护状态信息列表实时监控Salve节点的状态,该列表主要包含Slave节点唯一标识、心跳信号时间戳以及分配的任务集。Slave节点每隔一段时间向M aster节点发送心跳信号,由M aster节点更新状态信息列表中相应时间戳。该框架的容错机制主要是M aster节点通过判断时间戳间接判断Slave节点的在线或离线状态,所以,框架允许Slave节点随时加入或退出计算。
不同计算能力的Slave节点,完成任务集计算的速度不同。计算能力越强,申请的任务集个数越多,完成单个任务计算的速度越快,Master节点为其分配更多地任务集。因此,基于任务队列的机制可以解决计算节点间的负载均衡问题。
M aster节点从各Slave节点收集各个任务集相应的计算结果,最终将所有任务集的计算结果通过指定计算汇总成最终结果。
2.2 Slave节点
Slave节点的主要任务包括:申请加入计算,评价自身性能并接收计算子任务和计算数据,完成对子任务的计算,向M aster节点返回计算结果集以及定时向M aster节点发送心跳信号。
Slave节点申请加入计算,则先由M aster节点发送计算所需的网络拓扑等相关数据,通过Slave节点主机的计算性能指标申请任务个数,性能指标主要包括可提供的CPU核心数、内存大小以及是否有GPU参与计算等。由M aster节点为其分配相应的任务个数。Slave节点可以在计算过程中动态调整分配计算的CPU核心数以实现本地多线程之间的负载均衡,所以,完成任务并回传结果后,重新评测计算性能申请任务。
Slave节点每隔一段时间发送心跳信号,便于M aster节点及时了解其状态。
3 计算框架的实现及评估
平均最短路径是复杂网络的一个基本拓扑特征指标,它能够体现网络是否具有小世界性质,全局效率则反映了网络之间节点发送消息的平均效率。有向网络和无向网络的平均最短路径计算公式和全局效率计算公式分别如式(1)~式(4)所示,其中,N为网络节点数;dij表示节点i和节点j之间的最短路径长度。而这些指标要求计算网络中每一对节点间的最短路径长度,这对于大尺度的复杂网络来说是一个很耗时的过程。本文基于上述针对大尺度网络分析的志愿计算框架的设计,实现了该框架下的大尺度网络平均最短路径长度及全局效率的分布式计算。在具体实现中,采用了ICE中间件作为网络通信组件,该中间件具有实现简单、与平台和语言无关的优点。
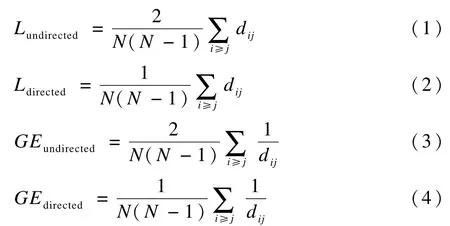
为了在分布式的志愿计算框架下实现平均最短路径和全局效率的计算,首先要实现算法的并行化。这里只需对每个节点调用经典的单源最短路径算法即可,然后根据式(1)或式(2)求得平均最短路径长度,根据式(3)或式(4)求得全局效率。由于每个节点间计算单源最短路径是相互独立的,很容易基于每个节点将算法并行化。
基于分布式的志愿计算框架实现了大尺度网络的平均最短路径和全局效率算法后,实验选用1台服务器作为M aster节点,8台不同配置、位于不同网段的计算机作为Slave节点共同参与计算,通过多组实验对框架进行测试和评估。各台计算机的硬件、软件配置情况如表1所示,其中,M表示Master节点;S表示Slave节点。
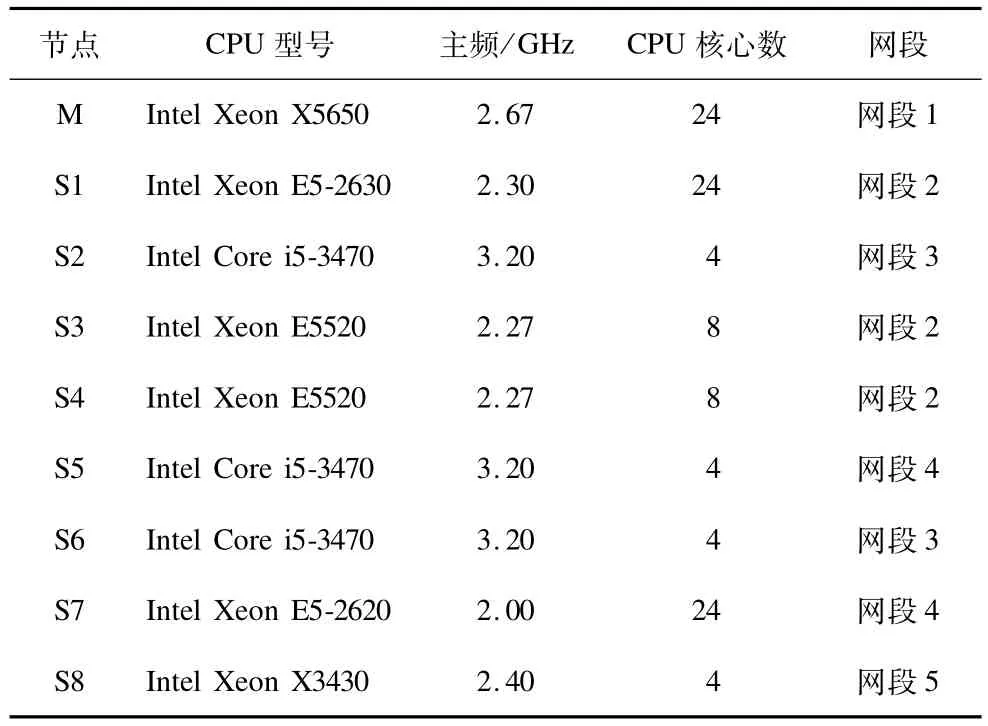
表1 实验环境配置
3.1 任务规模的影响
本节测试任务规模与计算时间之间的关系。实验测试数据为一个具有158 378个节点、851 968条边的无向网络,实验环境为8个Slave节点同时参与计算。通过递增任务规模(单个任务包含节点个数)的方式得到计算时间。经一组实验,得到的计算时间如表2所示。

表2 不同任务规模下的计算时间s
由表2可知,随着任务规模的增加,计算时间相对有一定减少,但是相对于整个任务的计算来看并不是很明显,并且任务规模到一定程度,计算时间几乎不变,由此设定任务规模为500,即每500个节点作为一个任务集。
3.2 Slave节点个数的影响
本节测试在任务规模一定的情况下,Slave节点的个数对计算时间的影响。采用5组数据作为基础数据,每组数据的基本信息如表3所示。
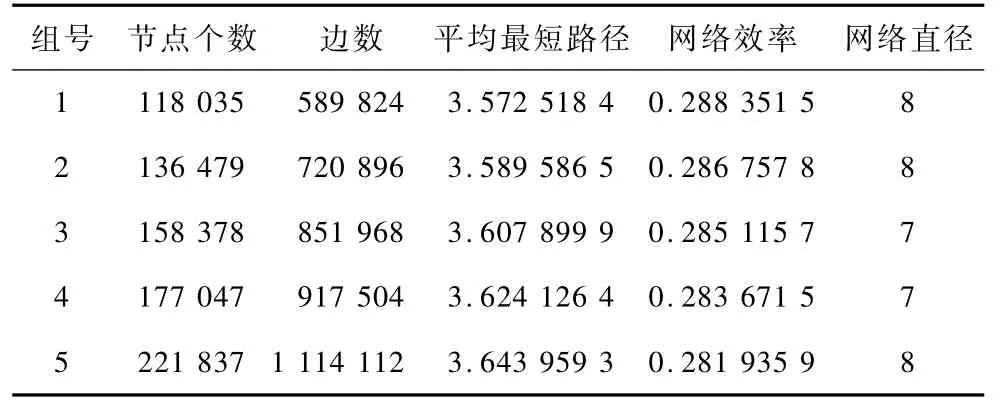
表3 实验数据

表4 不同节点个数下的计算时间s
由图2也可以看出,对同一个复杂网络的数据来说,当增加Slave节点的个数,计算时间逐渐减小,但是时间减小的幅度也越来越小。同时,对不同数据来说,数据量越大计算时间减小幅度越明显。总体计算时间是由节点计算时间和网络通信等额外时间共同组成,数据量越小,任务分配越频繁,通信额外时间越多,所以,减小幅度越不明显。

图2 同一网络中Slave个数与计算时间的关系
经过实验证明,本文设计的针对复杂网络计算的分布式框架是有效的,可以有效利用分散于网络中的计算资源,使其共同参与到处理含有上千万甚至上亿个节点的复杂网络计算中。
4 结束语
针对大尺度复杂网络的高性能分析计算问题,本文设计并实现了一个基于志愿计算思想的松耦合分布式计算框架。实验结果表明,该框架可以将网络中多台不同硬件配置、不同操作系统的计算机闲置资源通过局域网或广域网连接起来,在保证计算结果正确的前提下,共同参与大尺度复杂网络的快速分析与计算。
在下一步的工作中,主要拟解决以下3个问题:(1)将计算功能从服务端剥离,并进一步抽象框架的接口,实现不同算法的插件化选择和配置;(2)实现客户端异构计算资源的匹配和调用,如GPU计算;(3)实现大尺度复杂网络数据的P2P传输,从而降低服务端在数据传输方面的负载。
[1] 周 涛,张子柯,陈观荣,等.复杂网络研究的机遇与挑战[J].电子科技大学学报,2014,43(1):1-5.
[2] Bader D A,Madduri K.Designing Multithreaded Algorithm s for Breadth-first Search and st-connectivity on the Cray MTA-2[C]//Proceedings of ICPP'06. Washington D.C.,USA:IEEE Press,2006:523-530.
[3] Bader D A,Madduri K.Parallel Algorithm s for Evaluating Centrality Indices in Real-world Networks[C]// Proceedings of ICPP'06.Washington D.C.,USA:IEEE Press,2006:539-550.
[4] Zhao Xiaohan,Sala A,Zheng Haitao,et al.Efficient Shortest Paths on Massive Social Graphs[C]// Proceedings of the 7th International Conference on Collaborative Computing:Networking,Applications and Worksharing.Orlando,USA:[s.n.],2011:77-86.
[5] Hardin D S,Hardin S S.ACL2 Meets the GPU:Formalizing a CUDA-based Parallelizable A ll-pairs Shortest Path Algorithm in ACL2[C]//Proceedings of ACL2'13.[S.l.]:EPTCS,2013:127-142.
[6] 郭绍忠,王 伟,周 刚,等.基于GPU的单源最短路径算法设计与实现[J].计算机工程,2012,38(2):42-44.
[7] Pandey M,Pandey H,Sharma S.In-place Recursive Approach for A ll-pairs Shortest-path Problem Using OPENCL[C]//Proceedings of ICIT'13.Washington D.C.,USA:IEEE Press,2013.
[8] Ortega-Arranz H,Torres Y,Llanos D R,et al.The Allpair Shortest-path Problem in Shared-memory Heterogeneous Systems[EB/OL].(2013-01-03).http://www. infor.uva.es/~yuri.torres/docs/hector-Complex-2013.pdf.
[9] Sariyüce A E.Betweenness Centrality on GPUs and Heterogeneous Architectures[C]//Proceedings of the 6 th Workshop on General Purpose Processor Using Graphics Processing Units.New York,USA:ACM Press,2013.
[10] Aapo K,B lelloch G E,Guestrin C.GraphChi:Largescale Graph Computation on Just a PC[C]// Proceedings of OSDI'12.Washington D.C.,USA:IEEE Press,2012:31-46.
[11] Ediger D,Jiang K,Riedy J,et al.GraphCT:Multithreaded Algorithm s for Massive Graph Analysis[J]. IEEE Transactions on Parallel and Distributed System s,2013,24(11):2220-2229.
[12] Kang U,Tsourakakis C E.PEGASUS:A Peta-scale Graph Mining System Implementation and Observations[C]//Proceedings of ICDM'09.Washington D.C.,USA:IEEE Press,2009:229-238.
[13] Kang U,Tsourakakis C E,Appel A P,et al.HADI:Mining Radii of Large Graphs[J].ACM Transactions on Know ledge Discovery from Data,2011,5(8):1-8.
[14] Anderson D P.BOINC:A System for Public-resource Computing and Storage[C]//Proceedings of the 5th IEEE/ACM International Workshop on Grid Computing. Washington D.C.,USA:IEEE Press,2004:4-10.
[15] Anderson D P,Fedak G.The Computational and Storage Potential of Volunteer Computing[C]//Proceedings of the 6th IEEE International Symposium on Cluster Computing and the Grid.Washington D.C.,USA:IEEE Press,2006:73-80.
[16] Latora V,Marchiori M.Efficient Behavior of Small world Networks[J].Physical Review Letters,2001,87(19):1-4.
[17] Marquezan C,Righi R,Schnorr L M,et al.ICE:A Service Oriented Approach to Uniform the Access and Management of Cluster Environments[C]//Proceedings of Conference on Cluster Computing and the Grid. Washington D.C.,USA:IEEE Press,2006:54.
[18] 张俊军,章 旋.ICE中间件技术及其应用研究[J].计算机与现代化,2012,(5):192-194.
编辑 金胡考
Design and Implementation of Loose Coup ling Distributed Computing Framework for Com p lex Network
LU Gang,XU Qinliang,XU Nanshan,GUO Junxia
(College of Information Science and Technology,Beijing University of Chemical Technology,Beijing 100029,China)
In order to calculate the topological characteristics of large-scale com plex networks faster,a distributed computing framework for analyzing large-scale complex networks is designed and implemented in this paper.It collects loose coupling computing nodes distributed in the local network or the Internet.By using a task queue,Computing nodes can join or quit during Computing at any time.By fully leveraging the loose coupling Computing resources distributed in a network,the framework makes the speed of analyzing large-scale complex networks enhanced greatly.Based on this framework,the distributed computing of average length of the shortest paths and the efficiency of large-scale comp lex networks is implemented.Experimental results show that this framework can make full use of the idle Computing resources in the network,and greatly improves the Computing performance,on the premise of ensuring the correctness of computational results.
complex network;distributed Computing;Internet Communications Engine(ICE);loose coupling;M/S mode
卢 罡,徐勤良,许南山,等.复杂网络松耦合分布式计算框架的设计与实现[J].计算机工程,2015,41(11):73-76,93.
英文引用格式:Lu Gang,Xu Qinliang,Xu Nanshan,et al.Design and Implementation of Loose Coupling Distributed Computing Framework for Complex Network[J].Computer Engineering,2015,41(11):73-76,93.
1000-3428(2015)11-0073-04
A
TP391
10.3969/j.issn.1000-3428.2015.11.013
北京高等学校青年英才计划基金资助项目(YETP0506)。
卢 罡(1981-),男,讲师,主研方向:高性能计算,复杂网络;徐勤良,硕士研究生;许南山,副教授;郭俊霞(通讯作者),讲师。
2014-10-15
2014-12-11 E-m ail:guojx@mail.buct.edu.cn

