基于低冲突帮助机制的快速无等待哈希表算法

李鹏飞，张坤龙，康超凡

（天津大学计算机科学与技术学院，天津300072）

基于低冲突帮助机制的快速无等待哈希表算法

李鹏飞，张坤龙，康超凡

（天津大学计算机科学与技术学院，天津300072）

针对现有无等待哈希表算法未充分利用哈希表的固有并行性，造成线程之间存在高冲突和高冗余的问题，提出一种快速无等待哈希表算法。利用可冻结集合思想简化哈希表操作，采用CAS原子指令保证插入、删除与查找操作均为无等待。根据哈希表结构改进帮助机制，使得哈希桶的实现为无等待，只有在扩展哈希表时哈希桶之间才提供帮助。实验结果表明，该算法能降低线程操作间的冲突，提高帮助操作的并行度，当查找率为0、键值范围为0～256且线程数为8时，其吞吐率是现有无等待哈希表算法的2.5倍。

并发数据结构；哈希表；无等待；可线性化；可扩展

1 概述

在各种并发数据结构中，哈希表因能够在常数时间内完成操作而得到应用广泛。哈希表按照存储结构可分为封闭地址（closed address）哈希表和开放地址（open address）哈希表。前者元素存储在称为桶（bucket）的结构中，桶中可存放多个元素；后者元素存储在槽（slot）中，一个槽只能存放一个元素。哈希表通过散列函数将操作分散到不同的桶或槽，这使得彼此间的操作没有冲突，这就是固有并行性。如果哈希表能动态地扩张和收缩，则具有可扩展性。

2014年，Liu Yujie等人提出了动态可扩展的非阻塞封闭地址哈希表算法［1］，包括无锁（lock-free）哈希表算法和无等待（wait-free）哈希表算法。无锁和无等待［2］都具有非阻塞特性：一个线程的延迟不会影响其他线程的操作。其中无等待的演进性最强，它保证即使在其他线程干扰的情况下，每个线程都能在有限步内完成。

研究发现，虽然文献［1］中的无等待哈希表算法是目前性能最好的算法，但其性能却受到抑制。原因是该算法存在过多不必要的帮助，而且利用全局计数器来协调帮助造成了高争用。为了提升性能，文献［1］采用快路径慢路径（Fastpath/Slow path）机制［3］。其核心思想是尽可能地运行在无锁阶段（快路径），无等待阶段（慢路径）只是用来保证无等待特性，以此提升性能。然而，这种提升方法并没有从根本上解决无等待算法的性能瓶颈问题。为此，本文提出一种新的无等待哈希表算法，该算法要求哈希桶的实现是无等待的，并且只在哈希表调整时才提供帮助，从而充分利用哈希表的固有并行性。

2 相关工作

哈希表一直是热门的研究课题。在顺序数据结构中，哈希表算法层出不穷。然而，在共享数据结构中，并发环境下，非阻塞的哈希表算法仍是屈指可数。

文献［4］提出无锁封闭地址哈希表算法。该算法使用改进的Harris无锁链表［5］作为桶，通过散列函数将操作映射到相应桶上进行。算法能和内存管理方法相适应。然而，该算法不是可扩展的。

文献［6］提出动态可扩展的无锁封闭地址哈希表算法。但是该算法基于DCAS（Double Compare and Sw ap）原子指令［7］，DCAS在目前硬件结构中还不支持，而且软件模拟开销太大。

文献［8］提出动态可扩展的无锁开放地址哈希表算法。该算法在调整时有2个表：当前的旧哈希表和扩展后的新哈希表。在功能调整过程中，先标记旧哈希表中的数据元素，然后将标记的元素拷贝到新哈希表中，最后将完成拷贝的旧哈希表元素设置为特殊值，表示已被迁移。哈希表的操作在当前的旧哈希表上进行，一旦发现被标记的数据元素，就参与调整操作。调整结束后，新的哈希表成为当前的旧哈希表。该算法是真正意义上的可扩展哈希，可是该文中并没有给出算法的性能信息。

文献［9］提出无锁开放地址哈希表算法。该算法不具有可扩展性，但是可以重复利用元素删除后的空间，是空间有效的。

文献［10］提出递归有序划分可扩展哈希表算法，该算法的扩展方式为：不在桶内插入元素，而是在元素间插入桶。算法基于一个无锁的有序链表［5］和一个目录结构。链表中的元素分为数据元素和索引元素，这两者之间用最高位区分。元素按照它们的二进制比特位反转后排序，这样索引元素就实现了数据元素的有序划分。算法先在目录结构上找到相应的桶（没有则建立），然后通过桶找索引元素，若该索引元素的父索引还没建立，就递归建立。但是该算法并没有提供收缩的特性，而且索引元素一经建立就永不删除，并且算法还对内存的大小做了假设。

文献［11］采用完美哈希（perfect hash）的思想构造无等待可扩展哈希映射算法，能轻易实现哈希表。该算法使用一个桶数组，结构类似树：每个桶要么是一个数据项（叶子结点），要么指向一个数组（中间结点）。然而，算法实现的哈希表大小有上限，不是严格意义上可扩展的。

文献［12］提出无锁布谷哈希算法。布谷哈希（cuckoo hash）是开放地址哈希算法，使用2个独立的哈希表，每个哈希表有不同的散列函数。布谷哈希处理冲突时将某个表里存在的元素剔除，将新元素放入，而后将剔除的元素在另一个表上做类似操作，重复这个过程直到找到空槽将元素放入。无锁布谷哈希算法使用逻辑时钟策略解决查找丢失问题。插入操作使用帮助机制，保证了非阻塞特性。然而，该算法没有提供可扩展的功能，而且在最坏情况下，查找操作并不能在常数时间内完成。

动态可扩展的非阻塞封闭地址哈希表算法［1］的实现建立在抽象的可冻结集合上。可冻结集合提供冻结操作，集合在冻结之后，任何更新操作将会失败。可冻结集合可以由当前最新的无序链表实现［13］，也可以使用数组实现，以提高缓存特性。该算法有新表和旧表2个操作位置，2个表中的桶都由可冻结集合实现。在哈希表调整时，冻结旧表中的相应桶，使用写时复制（copy on w rite）机制，将桶中元素迁移至新表中的桶。元素迁移完后，新建一个空表，根据调整是扩张还是收缩设定空表的大小，然后将旧表置为空。此时新表成为“旧”表，新建的空表成为“新”表。算法通过哈希表在调整时维护新表和旧表的不变式关系，保证了操作的正确性。

3 算法设计

3.1 基本设计思想

无等待算法被认为是低效和难以实现的［14］，其很大原因在于帮助机制的设计［15］。大多数帮助机制存在两大缺陷：高冲突和高冗余［3］。在执行自己的操作之前，先帮助其他的线程，通常造成线程之间的高冲突。其实在大多数情况下，如果给定足够的时间，一个线程能自己完成操作。帮助机制必须设计成操作顺序一致，即并发帮助某个操作的线程执行过程是一样的，而该操作只能被正确的执行一次，这样就造成了高冗余。

文献［1］中的无等待算法使用一个全局共享的帮助数组，通过优先级决定帮助的次序，从而保证无等待特性。每个线程在完成自己的操作之前先扫描帮助数组，帮助完成优先级比自己高的操作。这种帮助机制没有考虑到封闭地址哈希表这种特殊的数据结构：哈希表具有双重结构，包括哈希框架和存放数据元素的桶。使用这种帮助机制，本来映射到不同桶上毫不相干的2个操作因为优先级的原因而不得不建立联系，没有充分利用哈希表的固有并行性，造成线程之间的高冲突和高冗余。

本文采用文献［1］的可冻结集合思想，使用CAS（Com pare and Sw ap）原子指令来实现无等待特性。为了更充分地利用哈希表的固有并行性，算法重新设计了帮助机制，具体表现在以下2个方面：（1）算法要求桶的实现必须是无等待的。然而与此不同的是文献［1］中桶的实现只要求无阻塞，一些快速的无锁链表算法，比如无锁链表算法［5］、LFList链表算法［13］与自组织链表算法［16］等均能够适用。（2）只有在哈希表进行调整时，哈希表上才提供帮助，而且只有调整线程才能帮助其他未完成操作的线程。这样在不同桶上做操作的线程之间不会相互干扰，降低了冲突，而只在必要时才提供帮助的策略提升了操作的并行度。

3.2 算法描述

3.2.1 集合中使用的结构

集合中使用的结构具体如下：

3.2.2 哈希表中使用的结构

哈希表中使用的结构具体如下：

3.3 算法分析

在文献［1］的基础上，可冻结集合算法中，record FSet增加了共享数组B，用于同一桶内的线程间相互帮助。函数Invoke是提供给上层的接口，插入和删除操作在FSet上通过调用Invoke而发生作用，更新集合（L50～L51，L50表示算法中代码的第50行，下同），然后通过GetResponse获取操作结果。查找操作通过调用HasM ember获得查找结果。只有当FSet中的元素需要迁移时才会调用Freeze。Freeze操作首先将可冻结标记置为true，随后调用DoFreeze冻结集合。Invoke中发现可冻结标记改变（L6），也帮助做冻结操作（L7）。

在哈希表算法中，插入和删除操作通过调用Apply获得相应的桶，若桶为空，则先进行收集（L90）。Apply调用期间，除了在同一个桶上调用Invoke而帮助相关线程之外，未做其他不相干的操作，提高了并行度。如果达到某种条件（L54，L59），则调用Resize对哈希表作调整（L55，L60）。Resize操作首先调用InitBucket对当前表（新表）做收集，将旧表中的元素迁移到新表中空的桶中（L97）。然后将指向旧表的指针置为空（L78），此时元素已全部迁移完成。最后新建一个空表，表的大小根据调整类型选择（L79），通过CAS原子操作使其成为新表（L82），收集后的表相应地成为旧表。

如果给定足够的时间，一个线程可能已经完成而并不需要其他线程的帮助：只有在必要时提供帮助才是合理的。基于此，新的无等待哈希表算法增加了函数HelpWhenResize（L108～L114），这是整个算法的关键。文献［1］中的算法不论操作是否在同一个桶上，只要优先级高于自己，就无条件帮助完成，很多时候这种帮助是不必要的。这样做的原因是为了保证无等待特性：防止其他线程在不断地调整而导致自己的操作始终不能完成的情况发生。函数HelpWhen Resize扫描哈希表的共享数组A中发布的操作（L109～L110），如果操作没完成（L111）且在当前桶上操作（L113），则在桶上帮助完成（L114）。函数HelpWhenResize只在调整时被调用（L77），不会出现线程由于调整干扰而不能完成的情形。

4 正确性证明

在并发环境下，正确性既包含了安全性（safety），也包含了活性（liveness）。所谓安全性，是指该数据结构实现了一个抽象数据结构，例如集合，并且实现是可线性化的（linearizable）［17］。并发系统的一次执行过程可以采用经历（history）模型来描述。经历是方法调用事件和响应事件的一个有限序列。可线性化隐含的基本思想是每个并发经历都等价于某个顺序经历，这样就将并发过程映射为顺序过程。所谓活性，也叫演进性，在使用锁的结构上指的是无死锁，无饥饿；在不使用锁的结构上指的是非阻塞特性。本文将从可线性化性和无等待特性2个方面进行证明。

4.1 可线性化特性

定义 集合中的元素来自哈希表新表、旧表中的元素，从哈希表元素到集合元素的映射关系定义如下：

（1）若新表中的桶b不为空，则桶b中元素属于集合。

（2）若新表中的桶b为空，且新表的大小是旧表的2倍，则旧表中满足L99～L100的桶中元素属于集合。

（3）若新表中的桶b为空，且旧表的大小是新表的2倍，则旧表中满足L102～L104的2个桶中元素属于集合。

引理1 插入或删除操作的可线性化的点在Invoke返回true时刻，即操作完成时刻L49。

引理2 查找操作的可线性化的点：若桶不是冻结的，则取在HasM ember（L71）上；否则，桶一定被某个Freeze操作冻结，可线性化的点取Freeze将冻结标记fflag设置为true（L19）或获取哈希表新表（L63）这2个操作中发生较晚的一个。

定理1 哈希表实现的抽象数据结构是集合。

证明：由引理1可知，在可线性化点对桶（FSet）进行插入操作：要么桶里没有插入操作的元素（L43结果为true），于是桶里增加了一个元素（L44）；要么L43结果为false，桶与先前一样。在可线性化点对桶进行删除操作：要么桶里没有删除操作的元素（L47结果为false），桶与先前一样；要么L47结果为true，于是桶里减少了一个元素（L47）。对于查找操作，由引理2可知，在调用HasM ember（b，k）返回操作结果时，对于操作的桶b（一定不为空），可能出现以下情况：（1）桶b没有被冻结，则桶b所在的表要么是新表，要么是旧表且新表的相应桶为空；由定义可知，相关元素在桶b中。（2）桶b被冻结，则桶b所在的表一定是旧表或已过时（既不是新表，又不是旧表）。若桶被冻结在执行L63之前，则执行L63时，将从L66获得桶b，由定义可知，相关元素在桶b中。若桶被冻结在执行L63之后，则直到桶b被冻结的时刻，桶b在旧表中且新表的相应桶为空，由定义可知，相关元素在桶b中。

4.2 无等待特性

引理3 一旦FSet的冻结标记fflag设置为true，则经过有限的操作步，FSet将被冻结（即执行L33成功）。

引理4 成为FSet的操作节点（执行L12成功）的更新操作节点，在有限步内不是自己完成就是别人帮助完成。

定理2 集合算法是无等待的。

证明：观察3.2节中的集合算法，发现只有函数DoFreeze与函数Invoke中有while循环。只有将冻结标记置为true才会调用函数DoFreeze，根据引理3，函数DoFreeze将在有限步内完成。函数Invoke中退出循环的条件是当前操作完成或该集合被冻结（L5）。若集合没被冻结，当前操作执行L12不能成功的原因是其他线程不断地干扰。假设线程总数为P，因为有帮助数组B，线程调用Invoke都会扫描一遍数组（L3），操作完成的线程再次运行时一定会发现这个未完成的操作，则最多经过P次操作完成，未完成的操作一定成为FSet的操作节点，由引理4可知，当前操作能在有限步内完成。若集合被冻结，则直接退出循环。

定理3 哈希表算法是无等待的。

证明：观察3.2节中的哈希表算法，发现只有函数Apply中有while循环。函数Apply不能结束的原因是操作始终没有完成。若哈希表没有发生调整，则每次调用函数Invoke将作用在同一个桶上，由定理2可知，函数Apply将在有限步内完成。若哈希表发生调整，函数HelpW henResize将扫描整个帮助数组（L109），调整线程将帮助未完成的操作。

5 实验与结果分析

实验在4核8线程（3.5 GHz，一级缓存64 KB，二级缓存256 KB）64 bit英特尔i7-4770K机器上进行，算法全都用Java实现。实验环境：Linux操作系统CentOS release 6.5，Java版本1.7.0-60。

实验的4个算法均是无等待的。其中，WFList是文献［1］中的算法，用文献［13］中的无锁无序链表实现桶；FastWFList是本文提出的算法，用文献［13］中的无等待无序链表实现桶；WFArray是文献［1］中算法的数组实现；FastWFA rray是本文算法的数组实现。

实验以吞吐率作为性能指标，为了避免调整操作对算法性能的影响，插入与删除操作的比率相同。操作数据在键值范围内随机生成。初始时哈希表中预先插入个数为键值范围一半的数据。实验参数如下：（1）函数contains，insert，remove的调用百分比有2种情况：1）0，50%，50%；2）80%，10%，10%。根据函数调用比例，线程随机地选择操作类型，主要考察冲突、争用的高低对算法性能的影响。（2）线程数目为1～8。（3）键值范围为0～256，0～65 536。主要考察键值范围大小对算法性能的影响。以上共4组实验，每组实验运行5次，每次运行5 s，最终结果取平均值。实验数据的标准偏差可忽略。实验结果见图1～图4。

图1 查找率为0、键值范围为0～256时的算法吞吐率

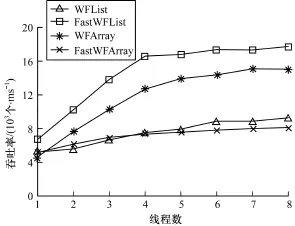
图2 查找率为0、键值范围为0～65 536时的算法吞吐率

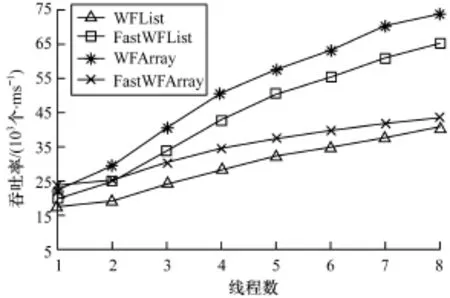
图3 查找率为80%、键值范围为0～256时的算法吞吐率

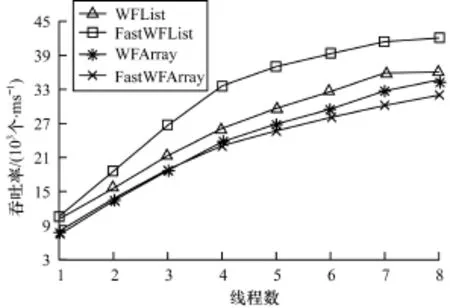
图4 查找率为80%、键值范围为0～65 536时的算法吞吐率

从图1～图4可以看出，本文算法的性能优于文献［1］算法，无论是链表实现还是数组实现。在相同的键值范围，查找率大的吞吐率较高。原因是查找并不改变集合元素，没有线程间的相互干扰，而且查找也不需要帮助，在相同时间内所做的操作更多。查找率为0时，各线程之间的竞争激烈。在图1中，随着线程数的增加，新算法的性能与文献［1］算法的性能差距越来越大，在线程数为8时吞吐率是其2.5倍。查找率为80%时，插入操作与删除操作发生冲突的概率较低，本文算法利用固有并行的优势减弱，提升的幅度降低。

在图2中，当线程数大于4时，本文算法的性能曲线趋于平缓，原因值得进一步研究。在小键值时，桶用数组实现的一类算法性能优于桶用链表实现的一类算法，而在大键值时情况正相反，可能是数组利用的缓存效应在大键值时优势不明显。

6 结束语

本文分析了无等待哈希表算法性能差的原因，根据哈希表的结构改进帮助机制，提出一种快速无等待哈希表算法，能更充分地利用哈希表的固有并行性。实验结果表明，该算法提高了无等待哈希表算法的性能下界，最好时是已知最快算法的2.5倍。下一步工作是分析大键值范围下本文算法性能趋于平缓的原因，以及在实际应用中使用并发数据结构，并结合多核并行运算的优势，进一步提高吞吐性能。

［1］ Liu Yujie，Zhang Kunlong，Spear M.Dynamic-sized Nonblocking Hash Tables［C］//Proceedings of 2014 ACM Symposium on Principles of Distributed Computing.Paris，France：ACM Press，2014：242-251.

［2］ Herlihy M.Wait-free Synchronization［J］.ACM Transactions on Programming Languages and Systems，1991，13（1）：124-149.

［3］ Kogan A，Petrank E.A Methodology for Creating Fast Wait-free Data Structures［C］//Proceedings of the 17th ACM SIGPLAN Symposium on Principles and Practice of Parallel Programming.New York，USA：ACM Press，2012：141-150.

［4］ M ichael M M.High Performance Dynamic Lock-free Hash Tables and List-based Sets［C］//Proceedings of the 14th Annual ACM Symposium on Parallel Algorithms and Architectures.New York，USA：ACM Press，2002：73-82.

［5］ Harris T L.A Pragmatic Implementation of Non-blocking Linked-lists［C］//Proceedings of the 15th International Conference on Distributed Computing.Berlin，Germany：Springer，2001：300-314.

［6］ Greenwald M.Two-handed Emulation：How to Build Nonblocking Implementations of Complex Data-structures Using DCAS［C］//Proceedings of the 21st Annual Symposium on Principles of Distributed Computing.New York， USA：ACM Press，2002：260-269.

［7］ Luchangco V，Moir M，Shavit N.Nonblocking k-comparesingle-swap［C］//Proceedings of the 15th Annual ACM Symposium on Parallel Algorithms and Architectures. New York，USA：ACM Press，2003：314-323.

［8］ Gao Hui，Groote J F，Hesselink W H.Lock-free Dynamic Hash Tables w ith Open Addressing［J］. Distributed Computing，2005，18（1）：21-42.

［9］ Purcell C，Harris T.Non-blocking Hashtables with Open Addressing［C］//Proceedings of the 19th International Conference on Distributed Computing.Berlin，Germany：Springer，2005：108-121.

［10］ Shalev O，Shavit N.Split-ordered Lists：Lock-free Extensible Hash Tables［J］.Journal of the ACM，2006，53（3）：379-405.

［11］ Feldman S，Laborde P，Dechev D.Concurrent Multilevel Arrays：Wait-free Extensible Hash Maps［C］// Proceedings of International Conference on Embedded Computing System s：Architectures，Modeling，and Simulation.Washington D.C.，USA：IEEE Press，2013：155-163.

［12］ Nguyen D N，Tsigas P.Lock-free Cuckoo Hashing［C］// Proceedings of the 34th International Conference on Distributed Computing Systems.Washington D.C.，USA：IEEE Computer Society，2014：627-636.

［13］ Zhang Kunlong，Zhao Yujiao，Yang Yajun，et al.Practical Non-blocking Unordered Lists［C］//Proceedings of the 27th International Conference on Distributed Computing. Berlin，Germany：Springer，2013：239-253.

［14］ Herlihy M，Shavit N.多处理器编程的艺术［M］.金 海，胡 侃，译.北京：机械工业出版社，2009.

［15］ Herlihy M，Luchangco V，Moir M.Obstruction-free Synchronization：Double-ended Queues as an Example［C］// Proceedings of the 23rd International Conference on Distributed Computing Systems.Washington D.C.，USA：IEEE Computer Society，2003：522-529.

［16］ 陈春光，张坤龙，谭龙飞，等.并发非阻塞自组织链表算法［J］.计算机工程，2013，39（8）：31-37.

［17］ Herlihy M P，W ing J M.Linearizability：A Correctness Condition for Concurrent Objects［J］.ACM Transactions on Programming Languages and System s，1990，12（3）：463-492.

编辑 陆燕菲

Fast Wait-free Hash Table Algorithm Based on Low-conflict Help Mechanism

LI Pengfei，ZHANG Kunlong，KANG Chaofan
（School of Computing Science and Technology，Tianjin University，Tianjin 300072，China）

Existing wait-free hash table algorithms do not take full advantage of the inherent parallelism of hash table，which results in the high redundancy and conflict between threads.In order to solve the problem，this paper proposes a fast wait-free hash table algorithm.It makes use of the freezable set to simplify the operations of hash table.And the Com pare and Swap（CAS）primitive is applied to realize the wait-free of insertion，deletion and search operations.It improves the help mechanism based on the structure of hash table to realize the wait-free of hash buckets.In order to avoid the conflics between the operations on different buckets，the help is given only when the hash table extends.Experimental results show that the algorithm can reduce the conflict between thread operation，and improve the parallelism of help operation.W hen the percentage of lookup is 0，the data range is 0～256 and the thread number reaches 8，throughput of the proposed algorithm is 2.5 times than the existing wait-free hash table algorithm.

concurrent data structure；hash table；wait-free；linearizability；extensibility

李鹏飞，张坤龙，康超凡.基于低冲突帮助机制的快速无等待哈希表算法［J］.计算机工程，2015，41（11）：52-58.

英文引用格式：Li Pengfei，Zhang Kunlong，Kang Chaofan.Fast Wait-free Hash Table Algorithm Based on Low-conflict Help Mechanism［J］.Computing Engineering，2015，41（11）：52-58.

1000-3428（2015）11-0052-07

A

TP311.1

10.3969/j.issn.1000-3428.2015.11.010

国家自然科学基金资助项目（61303021）；水利部公益性行业科研专项基金资助项目（201401033）。

李鹏飞（1990-），男，硕士研究生，主研方向：并发数据结构，数据库技术；张坤龙，副教授、博士；康超凡，硕士研究生。

2014-10-05

2014-12-15 E-m ail：lpf2013@tju.edu.cn