时标上的旅游景区电子商务竞争系统的稳定性

庞丽艳

（宁夏师范学院数学与计算机科学学院，宁夏，固原 756000）

近年来随着旅游业的发展，参与到旅游中的人、旅游公司及各景区的电子商务系统等也越来越多，很多学者已经将生态系统理论利用微分方程定性理论知识应用于经济学领域，诸如，Zhou[1]利用生物学中两个种群的模型研究了企业之间的共生问题；Guo[2]研究了基于生态模型的企业中的竞争问题；Zhi等[3]研究了基于生态系统理论的时标上的企业群模型的持久性和概周期解存在性；Li等[4]研究了基于生态系统理论的带有变时滞和反馈控制的企业束的概周期解存在性和渐进稳定性；Liu等[5]研究了带有时滞及反馈控制的竞争和共生的企业束模型的持久性；王文瑞等[6]做了基于省内外游客的沙漠旅游景区生态系统存在价值研究，是对生态学与旅游地理学的充分结合；由于电子商务生态系统可把景区内分散的景点、酒店、旅行社、旅游服务机构等组成一个完整的服务体系，可以利用网络的开放性和便捷性，整合游客分散的需求信息，实现旅游的需求和供给信息的串联，降低游客信息搜寻的成本，便于为游客定制个性化服务，提高竞争力，但正因为如此，使得各电子商务生态系统之间的竞争更加激烈。因此，在本篇文章中，考虑了下面系统的持久性、概周期解存在性与稳定性：

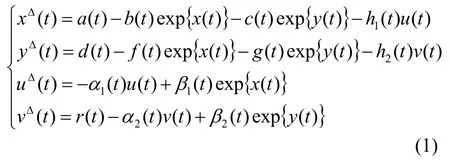
x( t ) ,y(t)分别代表同一景区同一服务行业（比如住宿业）的 A ,B两个不同电子商务系统的承载游客的规模； a ( t ) ,d(t)分别代表 A ,B两个不同电子商务系统的发展空间； c ( t ) ,f(t)分别代表 A ,B两个不同电子商务系统的发展迟滞系数； b ( t ) ,g(t)代表 A ,B两个不同电子商务系统的竞争系数； u ( t ) ,v(t)代表反馈控制量。

设T和 T+均为R的非空闭子集，f是T上的有界连续函数，定义：

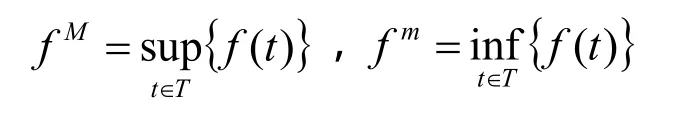
通篇假设：

其中+ℜ 是从T映到R的正回归函数。

1 准备知识

文中需要的定义可参考文献[3]。

引理2 假设Lyapunov函数满足下面的条件：

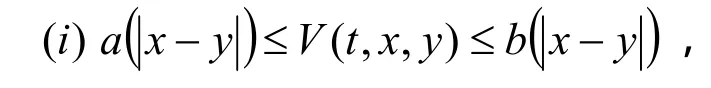
其中 a ,b ∈K,K={a∈C（ℜ+, ℜ+）:a(0)=0}，且 a (x)关于x递增；

若xΔ=f(t,x)存在一个解x(t)使得对所有t∈T+有x(t)∈S，其中S⊂D。则在S中存在唯一的一致渐进稳定的概周期解 p ( t)。

2 持久性

定理 1 假设 ( H1)成立，则系统 (1 )的每个解(x(t ),y(t ),u(t ),v(t ))T满足

证明：设 ( x(t),y(t ),u(t ),v(t ))T是系统 (1 )的任意解，由系统 (1 )的第一个方程得：

由引理1得：

则由系统 )1(的第一个方程得：

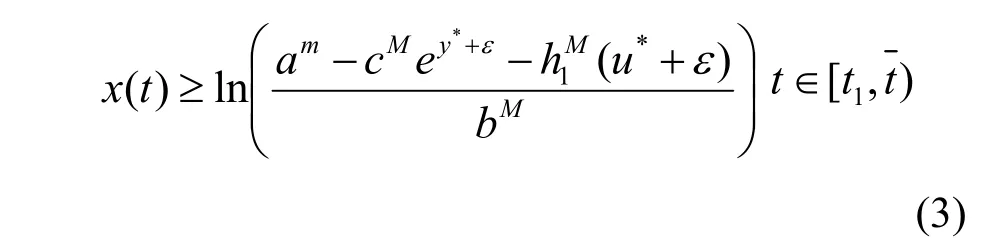
定理3 假设H(1)和H(2)成立，则系统(1)是持久的。

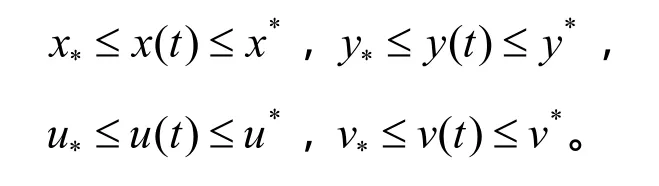
由定理1和定理2可得定理3是成立的，并且Ω是系统 )1(的不变集。

3 概周期解的存在性和稳定性

定理4 假设(H1)和(H2)成立，则Ω≠Θ。

证明：由于a(t),b(t),c(t),d(t),f(t),g(t),αi(t)，βi(t ) ,i=1,2均为概周期函数，则存在序列且当时，使得

定理 5 假设 ( H1)和 ( H2)成立，并进一步假设(H3)

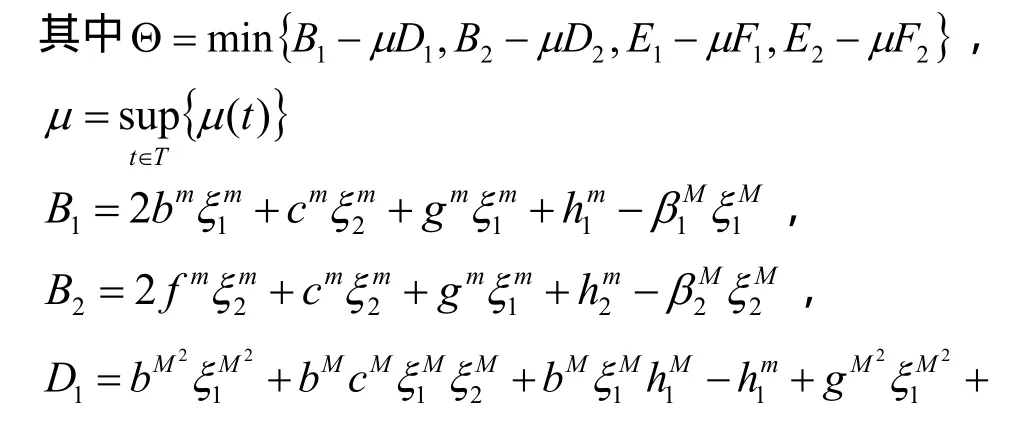
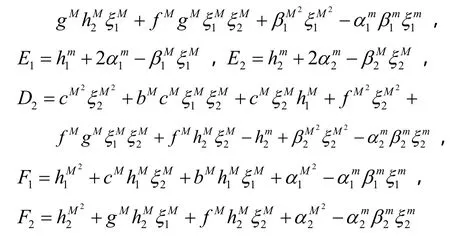
则系统 (1 ) 存在唯一的一致渐进稳定的概周期解X(t)= ( x(t ),y(t ),u(t ),v(t))T满足对所有 t ∈ T 有

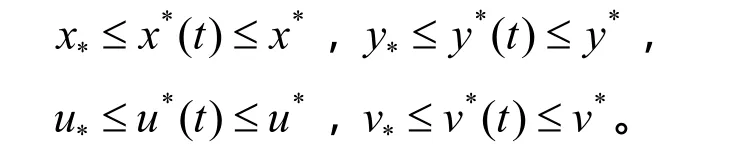
证明：由定理4得，系统 (1 )有有界解且对所有t∈ T 有，。

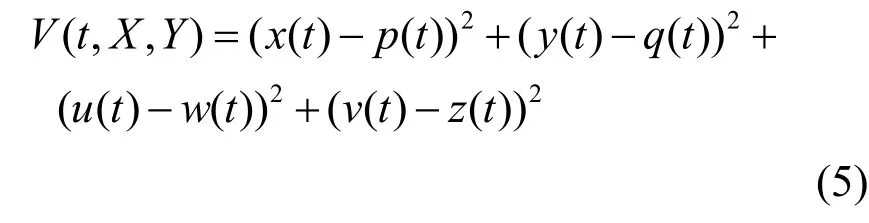
易得范数

因此引理2的条件 )(ii满足。

对 )5( 两边求积分得：

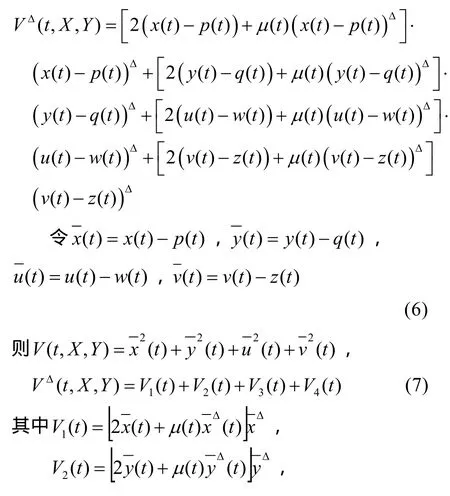
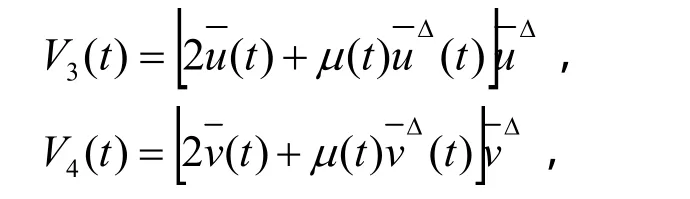
利用均值定理得到：

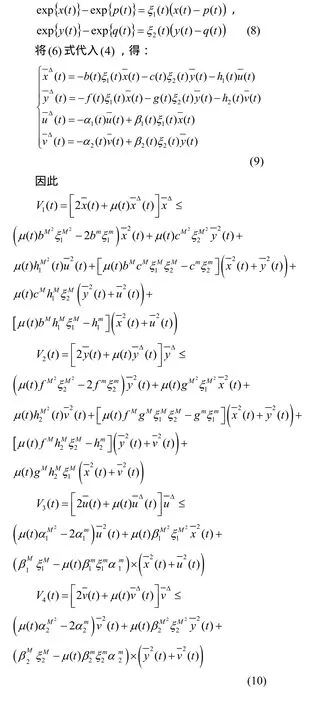
由(7)式和(10)式得

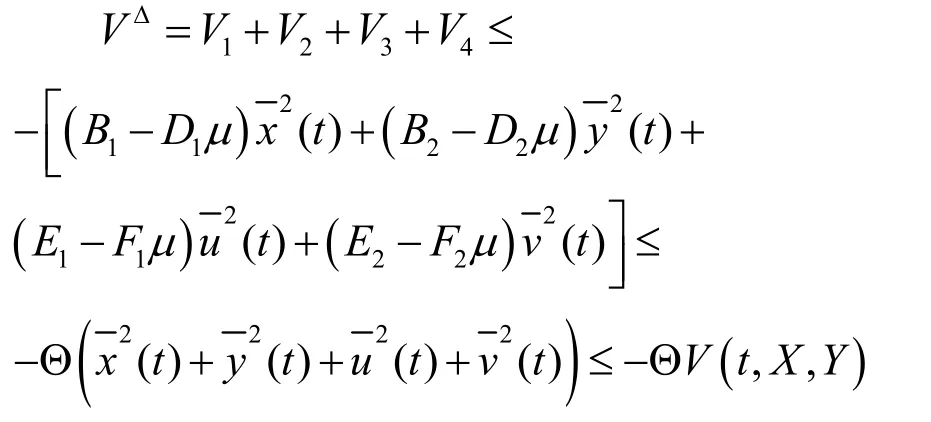
由（H3）得，引理2的条件（iii）满足，因此由引理 2，系统（1）存在唯一的一致渐进稳定的概周期解。

4 例子

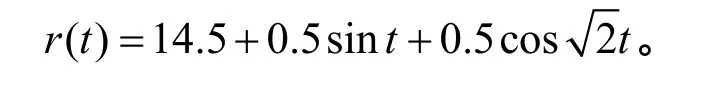
令 T =则系统(1)是持久的且有唯一的一致渐进稳定的概周期解。

证明：通过计算可得都满足定理3和定理5的条件，因此系统(1)是持久的并且存在唯一的一致渐进稳定的概周期解。证毕。

[1] Zhou H. Enterprise cluster co-existence model and stability analysis [J].System Engineering, 2003, 21(4):32-37 .

[2] Guo Q. Competitive strategies in an enterprise: an ecological model[J].Contem-porary Economic Management, 2005,27(2):49-52.

[3] Zhi Y H, Ding Z L，Li Y K. Permanence and almost periodic solution for an enterprise cluster model based on ecology theory with feedback controls on time scales[J].Discrete Dynamics in Nature and Society,2013,10:1-14.

[4] Li Y K，Zhang T W. Global asymptotical stability of a unique almost periodic solution for enterprise clusters based on ecology theory with time-varying delays and feedback controls[J]. Communications in Nonlinear Science and Numer-ical Simulation,2012,17(2): 904-913.

[5] Liu P ，Li Y K. Permanence for a competition and comperation model of enterprise cluster with delays and feedback controls [J].Electronic Journal of Differ-ential Equation , 2013,22:1-9.

[6] 王文瑞，叶宜好，王亚慧，等.基于省内外游客的沙漠旅游景区生态系统存在价值研究[J].云南师范大学学报:哲学社会科学版,2013,45(3):24-30.