桥用液压悬挂系统的疲劳分析

李安虎，兰强强，卞永明，刘广军

（同济大学机械与能源工程学院，上海 201804）

0 引言

桥梁作为跨越天然和人工障碍而修建的建筑物，给人们的出行、物资的运输带来了极大的便利。桥梁受载复杂，在运营过程中承受车辆载荷、人群载荷、风载及地震载荷等多种载荷复合作用，国内外因车辆载荷及风载作用导致的桥梁倒塌、人员伤亡事故屡见不鲜。究其原因，很多是由于桥梁本体失稳破坏或桥梁某些连接件在交变载荷作用下发生了疲劳破坏。因此，在现代桥梁设计时，桥梁本体失稳及其连接件的疲劳是必须考虑的重要问题。

有很多学者对桥梁本体失稳和桥梁部分连接件的疲劳做了相关研究。李莹等人对车辆荷载调查、模型车辆建立和Monte-Carlo方法模拟随机车辆建立了车辆随机载荷谱[1-2]。林梅等人通过实测在役桥梁危险杆件的应力应变历程，并结合雨流计数法及Miner线性累积损伤理论预估了在役桥梁的剩余疲劳寿命[3]。何维等人利用桥梁支座一个周期内承受的最大载荷和最小载荷对桥梁支座进行了疲劳分析[4]。李岩等人建立大桥风载概率模型，实现随机车载与风载联合作用下的拉索应力谱计算分析，基于累积损伤理论和Monte-Carlo法开展拉索的疲劳可靠度和疲劳寿命分析[5]。向渊等人在考虑构件存在初始裂纹的情况下基于断裂力学理论对桥梁连接件的风致疲劳问题[6]。可见，桥梁在车辆荷载及风载作用下的疲劳问题已得到学者们的广泛关注，但是面向桥梁活动连接如悬挂系统的疲劳研究鲜有报道。

本论文的研究对象为某沿海地区一座双层开启桥。该桥上层通车，下层行人并能开启。下层桥架的伸缩开启要求下层桥架与上层桥架的连接应为活动连接，必须采用活动悬挂系统。基于桥梁疲劳问题的重要性及其发生疲劳破坏的危害性，因此有必要对悬挂系统进行疲劳分析。由于风载的随机性以及悬挂系统竖直载荷的变化，且风载和竖直载荷为两个不同方向的力，因此真实的模拟载荷变化及如何对悬挂进行多轴疲劳分析成为本论文的关键。本分析基于workbench及Fe-safe对悬挂系统的疲劳寿命进行了预测，对该双层桥的悬挂系统安全可靠运行具有重要意义。

1 悬挂系统方案设计

悬挂系统作为上下层桥架连接的载体，在桥架闭合时，应能承受下层桥架恒重、风载和人群活载。在桥架需要开启时，悬挂系统应能够带动下层桥架沿一定方向(固定在上层桥架的悬挂导轨)移动。考虑到悬挂导轨表面加工精度及其安装精度，悬挂系统应能有位移补偿功能以防止下层桥架剧烈振动。

本文提出两种悬架设计方案：1.机械式悬挂系统；2.液压式悬挂系统。

1.1 机械式悬挂系统

该方案示意图如图1所示，用组合碟形弹簧受压承受载荷（最大载荷：恒载 167.50 kN+活载71.82 kN），并实现位移补偿，导向轮机构承受风载并在桥架开启时和悬挂轮一起实现桥架沿导轨开启。组合碟形弹簧依据承载要求设计，选用外径为140 mm的A类碟簧，组合方式为复合，三片叠合，三对对合，共9片碟簧，单片碟簧变形2.37 mm。

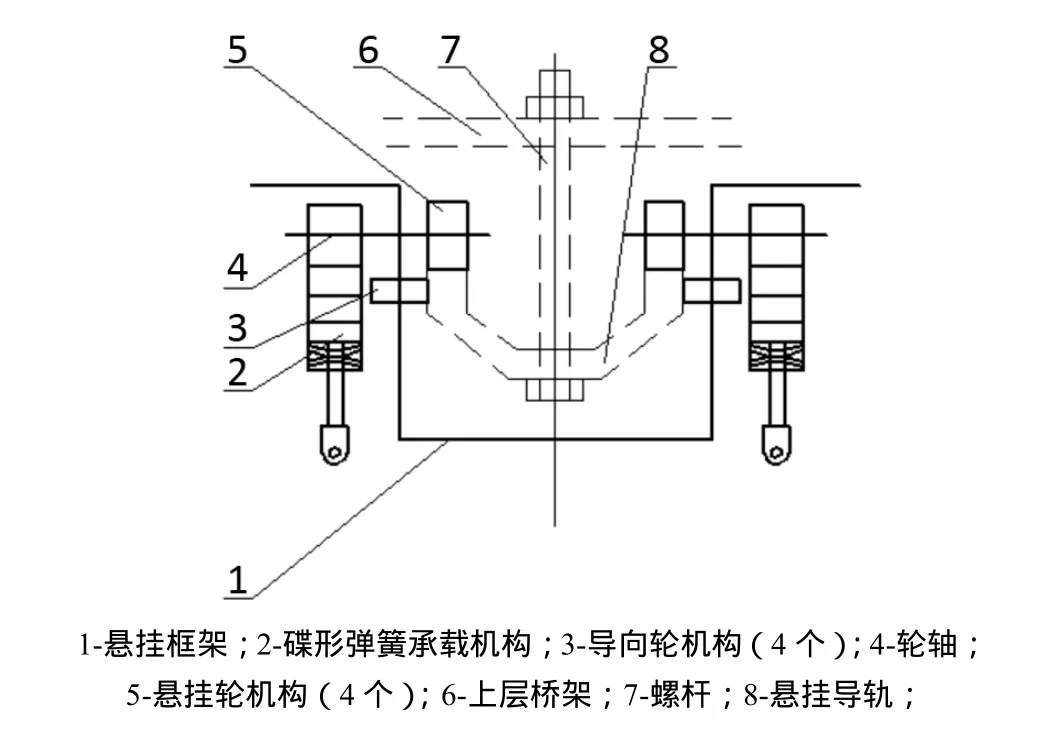
图1 机械式悬挂系统示意图Fig.1 The chart of mechanical suspension system

1.2 液压式悬挂方案

该方案示意图如图 2所示，通过液压油缸承受载荷（最大载荷：恒载167.50 kN+活载71.82 kN），在桥架开启过程中，油缸压力维持恒压以实现位移补偿，油缸行程50 mm，其他结构与机械式悬挂方案类似。

图2 液压式悬挂系统示意图Fig.2 The chart of hydraulic suspension system

由于机械式悬挂系统碟簧在桥架整个寿命期限内都承受载荷，故该悬挂系统无法对零部件进行更换，且因弹簧的变形量太小，该系统的位移补偿能力有限，导致悬挂导轨的加工安装精度高，两种方案的性能对比见表1。

由表1知，从悬挂位移补偿范围、导轨加工安装精度及维修方便性考虑，液压式悬挂方案优势明显，故选用液压式悬挂方案作为此开启桥的悬挂方案。

表1 两种悬挂系统方案性能对比Table 1 Performance comparison of two suspension system programs

悬挂系统在桥架运营时，承受的风载和竖直载荷随机变化，结构承受交变载荷时，当应力远小于结构的屈服强度时亦可发生破坏，且此破坏为突然破坏，危害巨大。因此，为保证悬挂系统在交变风载和竖直载荷作用下能够安全可靠的工作，有必要对其做进一步的疲劳分析。

2 疲劳分析

2.1 疲劳理论

疲劳是指由未超过金属材料强度极限的重复载荷作用，在结构构件上形成裂纹以及随着裂纹的扩展，并导致结构构件的损伤与破坏。从所受应力状态可将疲劳分为单轴疲劳和多轴疲劳。单轴疲劳是指材料或零件在单项循环应力作用下发生疲劳，多轴疲劳是指多向应力作用下的疲劳。由于悬挂系统承受竖直方向的桥架恒重及水平方向的交变风载，故此问题为多轴疲劳问题。

多轴疲劳是指多向应力或应变作用下的疲劳，多轴疲劳损伤发生在多轴循环加载条件下，加载过程中有两个或三个应力(或应变)分量独立地随时间发生周期性变化。多轴疲劳寿命的预测方法有基于应力的疲劳破坏准则、基于应变的疲劳破坏准则和循环塑性功的疲劳破坏理论。按疲劳寿命可将多轴疲劳分为多轴高周疲劳和多轴低周疲劳，一般的低周疲劳存在塑性变形，应力与应变为非线性关系，使用应变可更好地反映规律，因此主要考虑应变。应用较为广泛的主要有基于正应变或剪应变的疲劳损伤模型和基于临界面法的 Bannatine模型、Fatemi Socie模型、Wang-Brown模型、统一多轴疲劳损伤模型等[7-9]。而高周疲劳主要以应力为损伤控制参量，应用较为广泛的主要有基于最大正应力或剪应力的疲劳损伤模型、stress-based Brown Miller模型、基于等效应力的Basquin公式和基于临界面法的Sines模型、Findley模型、McDiarmid模型和Matake 模型等[10]。

基于悬挂系统竖直方向承受桥重、人群活载及水平方向承受风载作用，该结构的疲劳为多轴疲劳问题，现利用 Workbench及Fe-safe对该结构进行疲劳分析，其分析流程如图3所示。

图3 疲劳分析流程图Fig.3 The flowchart for fatigue analysis

本文研究的悬挂系统疲劳寿命属于多轴高周疲劳问题，在利用 Fe-safe计算结构疲劳时，首先运用雨流计数法对交变风载及恒载作用下的应力时间历程循环计数，然后采用 stress-based Brown Miller模型计算各个循环的损伤，最后运用 Miner线性损伤累积理论进行损伤累积和寿命估算。

stress-based Brown Miller模型认为疲劳裂纹出现在承受最大剪切应力幅的临界面上，疲劳损伤是关于剪切应力与法向正应力的函数，其寿命公式为：

其中，maxτΔ为最大切应力幅，nσΔ为法向正应力幅，fσ为材料疲劳极限，fN为疲劳寿命，b为材料的疲劳强度指数。

由于悬挂系统所承受的交变载荷并为对称载荷，需对其应力做平均应力修正，Goodman模型为直线模型，形式简单，修正结果安全，其修正公式为：

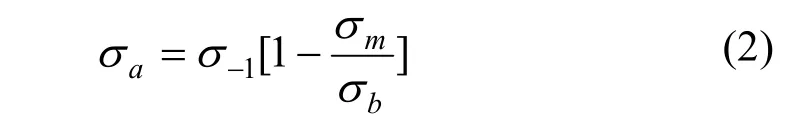
其中，σa为单个循环应力幅，为单个循环的平均应力，为材料抗拉强度极限，σ 为-1对称循环下的等效最大应力。

结构疲劳是由损伤逐渐累积到一定程度才发生的。Miner累积损伤理论认为每一应力循环会对结构产生一定的损伤，结构的总损伤为各应力循环作用下的损伤线性叠加，可表示为:

其中， ni为第i个应力循环作用的次数， Ni为第i个应力循环作用至疲劳的循环作用次数，若D≤ 1，则认为疲劳安全，反之则会发生疲劳破坏。

2.2 疲劳分析

（1）确定风速分布

根据统计调查分析，该地区的风速可近似服从威布尔分布：

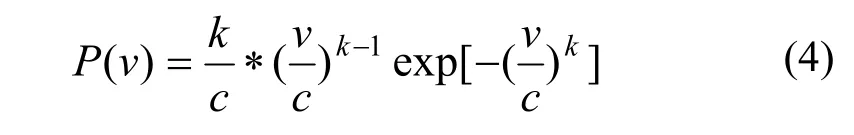
其中k为形状参数，c为尺度参数。

根据文献[11]，为简化计算，威布尔分布的形状参数k可取为2，尺度参数c按下式计算：

μ为某一地区的年平均风速，由该地区近 30年各月份的平均风速统计资料（表2）知，μ =5 m/s。

表2 该地区近30年各月份平均风速统计表Table 2 T he monthly average wind speed in the area for nearly 30 years

将μ = 5，k = 2代入上式，即可得c = 5.64，从而可得宁波北仑区的年风速服从分布：

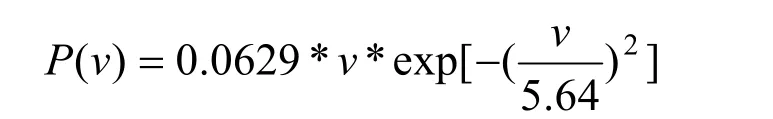
风速分布概率如图4所示。

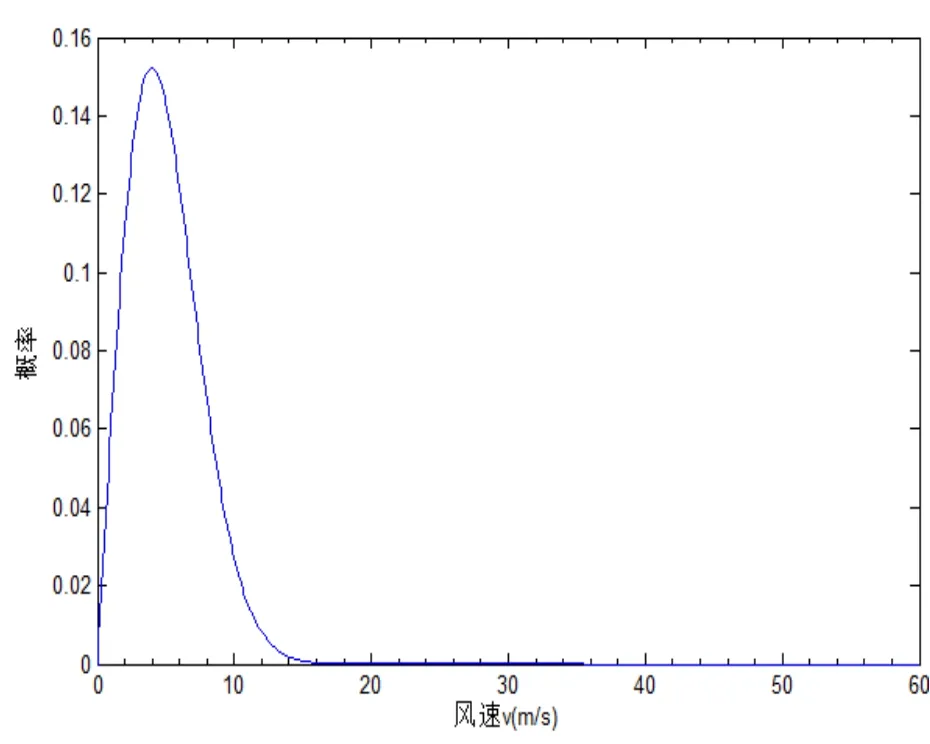
图4 风速分布概率Fig.4 Probability distribution map of wind speed

（2）确定随机风载谱

按《JTGT D60-01-2004公路桥梁抗风设计规范》，横桥向风作用下主梁单位长度上的横向静阵风载荷为：

式中， —空气密度，取 1.25 k g/m3；Vg—静阵风风速； CH—主梁的阻力系数；

当主梁截面带有斜腹板时， CH可以竖直方向为基准每倾斜1°折减0.5%，最多可折减30%；上部结构为两片或两片以上桁架时，所有迎风桁架的风载阻力系数均取ηCH，η为遮挡系数，根据《JTGT D60-01-2004公路桥梁抗风设计规范》取η=0.6；故最终取 CH=0.9435；

H—主梁的投影高度，此处为4.1 m。

单侧桥架承受的总风载：

l为单侧移动桥架长度，单侧桥架共5节，每节11 m，故l=55 m。将各物理量的数值代入式（6）和式（7），可得平均风速作用下单侧桥架总风载为∑ FH= 3 324N 。因为单侧桥架共有 20个导向轮承受风载，每个导向轮在平均风速作用下承受的风载为166 N。

根据该区年平均风速为5 m/s，每10 min钟统计一次平均风速，将平均风速为5 m/s的载荷（166 N）作为基准载荷，依据风速的随机性，在matlab中，利用随机函数及风载与风速的关系，模拟出基于基准载荷的风载载荷系数，如图5所示。

图5 基于平均风速的载荷系数图Fig.5 The chart of load factor based on an average wind speed

（3）确定竖直载荷谱

此桥为一座下层可开启的双层桥，上层通车，下层行人，悬挂系统竖直方向上承受桥重及人群活载。由一个悬挂系统承受桥重167.50 kN，每个悬挂系统有4个滚轮，滚轮支撑于悬挂导轨上，故在桥重作用下，每个悬挂滚轮承载41.875 kN。

由于竖直方向载荷除桥重外，还承受行人活载，而行人活载为一变化载荷。现通过调查发现该地区通过该桥梁的行人高峰期为早上七点至九点和下午四点至六点，此时，行人通行受阻；晚上22:00至早上6:00时间段桥上仅有极个别行人，此时，可忽略行人活载；在这两个时间段以外的其他时间行人自由通行。故可将一天中行人活载按三个阶段模拟：高峰期、自由通行期、无人通行期。由于对于高峰期和自由通行期两个阶段桥上行人数量可由正态分布描述，且对大量的群体密度和疏散流量的数据进行整理发现，当人口密度小于0.54人/m2时，人们可自由移动（自由通行期）；当人口密度超过3.8人/m2时，人们移动受阻（高峰期）。由单节桥架面积为126 m2及假设该地区人均体重60 kg，依据正态分布的3σ原则及单节桥架上悬挂滚轮的数量（16个），高峰期单个滚轮承受的活载服从分布N(8.98,2.992)，自由通行期单个滚轮承受的活载活载服从分布 N (1.28,0.432)，单位为kN。

由正态分布的特性，考虑桥重和活载的竖直载荷也服从正态分布，该正态分布只改变均值，不改变方差。故高峰期单个滚轮承受的竖直载荷服从分布N(50.86,2.992)，自由通行期单个滚轮承受的竖直载荷服从分布 N (43.16,0.432)，单位为kN。利用随机函数在matlab中模拟一天（早上6点到晚上24:00）中滚轮承受的载荷与其载荷均值（50.86 kN）的比值，得到悬挂系统滚轮承受的竖直载荷谱如图6所示。

图6 基于平均竖直载荷的竖直载荷系数图Fig.6 The chart of the vertical load factor based on the average vertical load

2.3 疲劳计算

（1）网格划分

取单个悬挂系统进行计算。采用 ANSYS Workbench有限元软件对悬挂系统进行网格划分，部件之间采用绑定接触，有限元模型如图7所示。

图7 悬挂系统有限元模型Fig.7 The finite element model of the suspension system

（2）建立有限元模型

由悬挂示意图2知，悬挂系统油缸与下层桥架通过销轴相连，悬挂轮支撑在导轨上，导向轮装在悬挂框架迎风侧，故在对悬挂系统有限元模型加载时，可将桥重及人群活载均值添加在4个悬挂轮上，大小为50860 N，方向沿X轴正向，风载添加在导向轮上，大小为166 N，方向沿Z轴正向，风载与竖直载荷按两个载荷步加载，油缸吊耳处添加圆柱副，并释放其切向自由度，载荷及约束施加情况如图8。

图8 悬挂系统载荷约束施加图Fig.8 The chart of constraints and load imposed for the suspension system

（3）静应力计算

将上述悬挂系统有限元模型在workbench中求解，得到其应力及综合变形结果如图9和图10所示，最大应力为144.78 MPa，发生在图示椭圆圈住的滚轮机构附近，最大变形为2.15 mm，发生在滚轮机构上，悬挂主体材料为 Q345，强度和刚度满足要求。

图9 悬挂系统静应力图Fig.9 The chart of static stress for the suspension system

图10 悬挂系统静变形图Fig.10 The chart of deformation for the suspension system

（4）疲劳寿命计算

悬挂系统承受竖直载荷及水平风载两个方向的力作用，故不能将其当做单向应力状态进行疲劳求解。将workbench有限元分析 rst结果文件导入Fe-safe中，对水平风载添加图5风载谱，对竖直载荷施添加图6的载荷谱，设置相关材料参数后，即可进行疲劳分析。由于 Fe-safe无法对结果进行后处理，需将结果导入 Ansys中，最终结果如图 11所示。

图11 悬挂系统疲劳寿命图Fig.11 The fatigue life chart of the suspension system

我国桥梁设计寿命为100年，由于在进行疲劳分析时，导入的载荷谱为一天的风载谱。由于对处于结构高周疲劳区（载荷循环次数 ＞ 1 04）的随机疲劳载荷，Miner线性累积损伤理论已足够适用，而Miner线性累积损伤理论认为：各个应力之间相互独立互不相关，各应力循环作用下导致结构产生的损伤可线性累加，故可将100年的设计寿命等效为悬挂导向机构承受36500块载荷谱。由图11可知，悬挂导向机构能承受的最小载荷谱块数为 1×107＞36500，故疲劳满足要求；由此也说明疲劳足够满足要求，且一天中风载变化频率远小于分析所用载荷谱。综上，悬挂导向机构在设计寿命内在交变风载、桥重及人群活载的作用下满足疲劳要求。

3 结论

本文通过workbench及Fe-safe的联合应用，对某沿海地区某双层开启桥的悬挂导向机构进行多轴疲劳仿真分析，验证了悬挂系统在桥架设计寿命内疲劳满足要求。本文所采用的分析方法不仅为该双层开启桥的安全使用提供了依据，而且为解决结构类似多轴随机疲劳问题提供了思路，对结构的疲劳分析亦可确定结构疲劳危险部位及寿命，为结构的维修保养提供了理论依据。

[1] Kalos M H. Monte Carlo Methods. New York:John Wiley and Sons,1986.

[2] 李莹. 公路钢桥疲劳性能及可靠性研究[D]. 哈尔滨：哈尔滨工业大学,2008.

[3] 林梅等. 钢桥疲劳性能及剩余寿命研究[D]. 兰州：兰州理工大学,2011.

[4] 何维等. 桥梁支座结构分析及疲劳性能研究[D].成都：西南交通大学,2011.

[5] 李岩,吕大刚. 考虑随机车载，风载联合作用的斜拉桥拉索疲劳可靠性分析[J].中国公路学报,2012,25(2)：60-66.

[6] 向渊. 悬索桥钢箱梁临时连接件风致疲劳分析[D]. 成都:西南交通大学,2009.

[7] Bannanline, J A. A variable amplitude multiaxial fatigue life prediction method [D ]. [S.l.]: University of Illinois at Urbana-Champaign, 1989.

[8] Fatemi A, Socie D F. A critical plane approach to multiaxial fatigue damage including out-of-phase loading[J]. Fatigue&Fracture of Engineering Materials&Structures. 1988. 11(3): 149.

[9] [9] Wang C H, Brown M W. Life prediction techniques for variable amplitude multiaxial fatigue-part2:comparison experimental results[J]. Journal of Engineering Materials Technology, 1996, 118(3): 371.

[10] Karolcauk A, Macha E. A review of critical plane orientations in multiaxial fatigue failure criteria of metallic materials[J]. lnternational journal of Fracture,2005, 134(3-4): 267-304.

[11] 林迟，欧进萍. 基于结构全寿命设计需求的疲劳风速谱模型与参数[J].自然灾害学报,2014,23(2):77-84.