基于立体视觉的机器人位姿标定技术研究

吴年祥 ，邹华东

（1.中国地质大学自动化学院，湖北，武汉 430074；2.安徽国防科技职业学院机电工程系，安徽，六安 237001）

0 引言

随着工业技术的迅速发展，机器人技术在机械、机电、汽车、电子等行业担任着重要角色。在柔性自动生产线中，机器人机械手的抓取、放置、装配、焊接等应用最广泛。然而，产品竞争日益激烈，产品质量的不断提高，要求工业机器人能在机电一体化等生产中完成三维空间精确操作，因此，基于视觉的机器人外部位姿标定技术的研究显得尤为重要。机器人外部位姿是指确定机器人世界坐标系和基础坐标系及工件坐标系之间的关系[1]。而在机器人基坐标系固定情况下，通常将其与世界人坐标系设置重合，从而确定机器人基坐标系与工件坐标系之间的坐标变换关系即机器人外部位姿。本文通过分步标定法之一的机器人外部位姿来确定机器人工件坐标系与基坐标系之间的坐标变换关系，从而确定机器人工件坐标系与立体视觉传感器坐标系之间的关系[2]。

1 机器人双目立体视觉传感器的三坐标数学模型

机器人双目立体视觉在计量测量技术领域的作用充分体现灵活的运动性、通用性。通过安装在机器人末端手关节上的左右放置的双目激光立体视觉传感器获取空间点的三维信息。其双目立体视觉测量示意图如图1所示，数学模型如图2所示。被测工件与末端关节左右相对固定的立体视觉传感器构成三角形，被测工件在两台摄像机上呈现立体图像时，匹配相关的特征点，采用最小二乘法，计算左右两幅图像的视觉差异获得空间特征点的三维坐标位置。

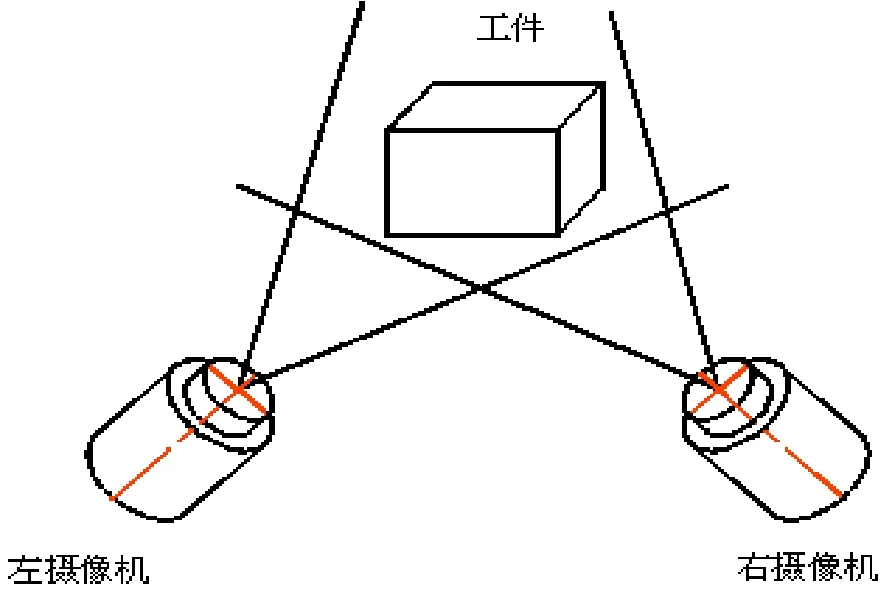
图1 双目立体视觉传感器测量示意图、Fig.1 Schematic of binocular stereo vision sensor measurement

左、右两个相对位置固定的视觉传感器所处的空间关系如式（1）所示：

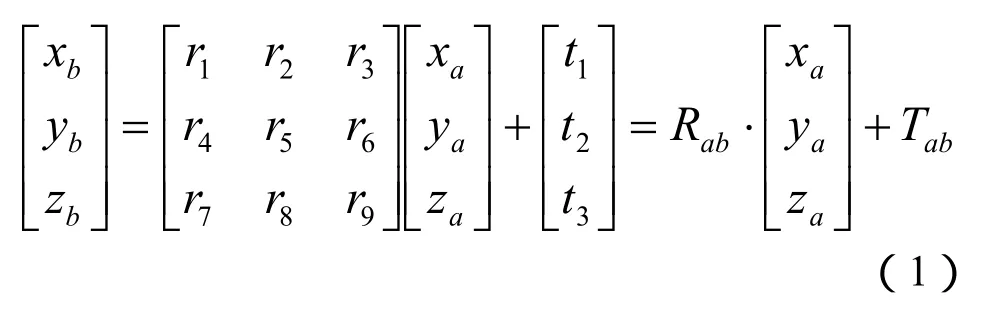
其中视觉传感器的两个外部参数即左、右相对位置摄像机坐标系间的平移矢量与旋转矩阵分别用Tab和Rab来表示。联立式（1）中的(xb,yb,zb)三个方程，利用最小二乘算法求解该式，可以获得视觉传感器坐标系下空间特征点的三维坐标位置：

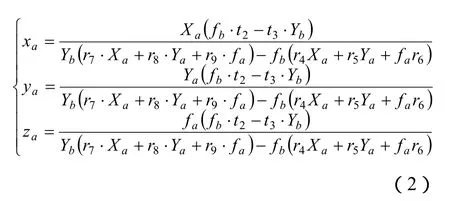
式（2）右边的固定参数可以通过摄像机传感器内部与外部参数的标定方法获得[3-4]。因此，在双目立体视觉传感器下，以上数学模型的建立可以获得空间被测点三维位置的信息(xa, ya, za)T。通过机器人手眼关系和靶标法可以间接得出空间任意有效被测点时机器人工件坐标系和视觉传感器坐标系之间的坐标变换关系。

2 机器人外部位姿标定方式

2.1 机器人位姿方程的建立与求解方法

如图2所示，按照Shiu[5]手眼标定算法以及机器人系统坐标变换链的闭合特征，用矩阵A来表示工件坐标和视觉传感器件坐标系之间的位置关系，矩阵T表示工件坐标系和机器人基坐标系之间的位置关系，未知位置关系X表示视觉传感器坐标系与机器人末端关节坐标系之间的齐次坐标变换矩阵，矩阵 H表示机器人基坐标系相对于机器人末端关节的位姿。经过机器人视觉传感器坐标系到末端关节坐标系以及基坐标系的齐次坐标相关变换X·H，可以将任意空间位置点的坐标统一转换至基坐标系下[6]。

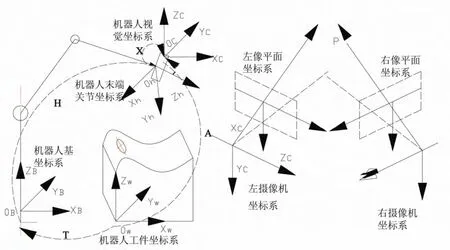
图2 机器人外部位姿标定与视觉传感器测量模型图Fig.2 Bobot clibration of external pose and vision sensor measurement model diagram

由图2可知，该位姿标定坐标变换链的闭合特征，可以得出: A = T · H · X （3）

通过先求解工件坐标和视觉传感器坐标系之间的位置矩阵关系A，可以求解矩阵T。由式（4）齐次矩阵坐标方程的变换，可以将经过标定后的视觉传感器特征点的空间三维坐标值转移到工件坐标系下。如果空间有若干个点 Pi(i ≥ 4 )，经过其空间点的齐次坐标相关变换H·X，可以由在其工件坐标系下的坐标位置(转换为基坐标系下的坐标位置(。

式（5）中就是所求机器人外部位姿T，即工件坐标系和机器人基坐标系之间的位置关系，而 T矩阵中的旋转子矩阵依据正交约束方式建立方程为非线性，求解困难。为简化方程，使用坐标空间多点采集方法，确立线性方程求解。

对于一个空间点可以列出三个位置方向方程，假设有四个已知点的坐标值 ()分别代入式（5），可以得出矩阵A中的12个不相关的未知量方程：

将式（7-10）合并转换成矩阵形式，可以得到式（19）：

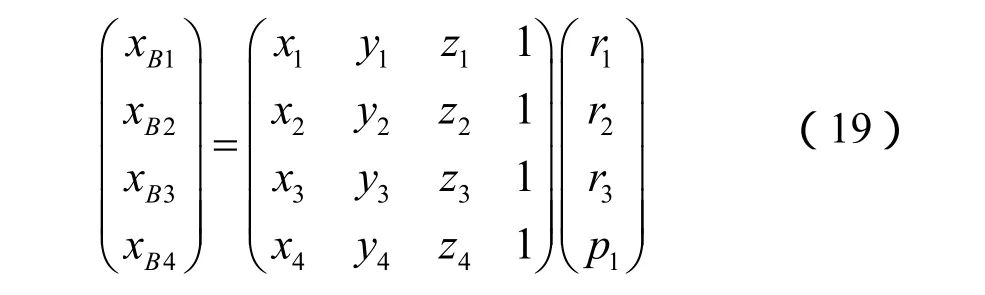
将式（19）的四元一次方程组利用高斯消去法（Gaussian Elimination）可以直接求解得到未知数：r1、r2、r3、p1。同理，将式（11-14）和式（15-18）合并转换成矩阵形式，可以得到式（20）、（21）：

同理，再通过高斯消去法求解 r4、r5、r6、p2和r7、r8、r9、p3矩阵。进而求得机器人外部外姿工件坐标系与机器人基坐标系之间的位置关系矩阵T。

在实际应用当中，考虑到各种坐标系下的坐标值存在噪声误差，为了进一步提高精度，可进一步采用最小二乘法拟合，将方程组（19-21）简化成D C Y= · 矩阵方程形式：

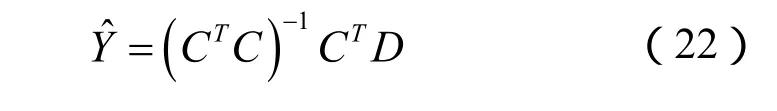
式（22）为每一个方程组所对应的未知量向量，也同样可以得出机器人的外部位姿。

2.2 机器人外部位姿的工具与标定方式

通过以下靶标法来确定机器人在某一位姿时工件坐标系和机器人视觉传感器坐标系之间齐次坐标变换矩阵A。如图3所示，首先让机器人固定在某一静态位姿；其次利用CMM（三坐标测量机）标定一个定位夹，可以得到其夹具坐标系和靶标坐标系之间的精确位置关系；最后将圆形平面靶标定位安装到工件坐标系范围内，并且让其工件定位基准和夹具定位基准重合，从而保证它们之间的坐标系重合。

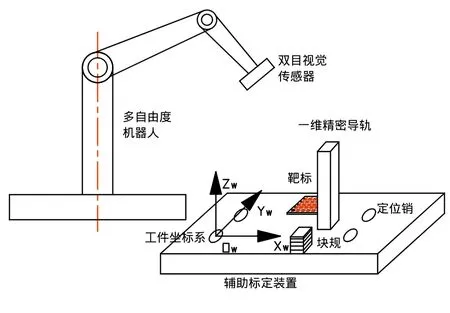
图3 靶标法示意图Fig.3 Sketch of bar method

在测量当中，圆形平面的靶标配合一维精密导轨和组合量块的使用，使靶标能够在视觉传感器的可视范围内移动，从而可以采集更多的空间已知坐标点。经过已标定的工件坐标系和靶标坐标系的关系，从而得出视觉传感器所采集到的空间特征点在工件坐标系下的坐标值也是已知的，再利用2.1机器人位姿方程的建立与求解方式可以得出齐次坐标变换矩阵A。综上所述，可知该靶标法利用了机器人在某一静态位姿时的相关值进行了机器人在任意状态时都固定不变的机器人外部位姿的求解[7]。

3 模拟研究实验

本实验采用模拟实验方法来初步验证基本立体视觉的机器人位姿标定程序设计算法的测量精度。

假设机器人实际外部位姿其中的一组数据矩阵为：

并假定，位于工件坐标系下四个位置点p1、p2、p3、p4的坐标值分别为(1.5,2.0,3.3)T，(30.2,-5.7,8.9)T，(102.4,70.7,59.8)T，(-40.6,89.9,-50.4)T，分别代入式（5），通过矩阵整理和运算，可以得出在机器人基础坐标系下四个位置点的坐标值分别为：

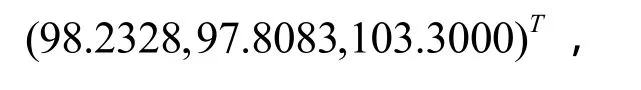
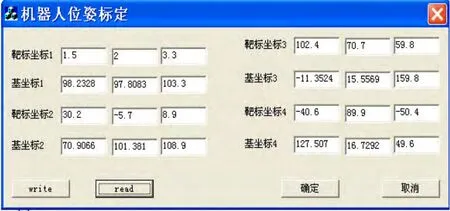
图4 外部位姿标定求解Fig.4 Solution of equations calibration of external pose

如图5所示。

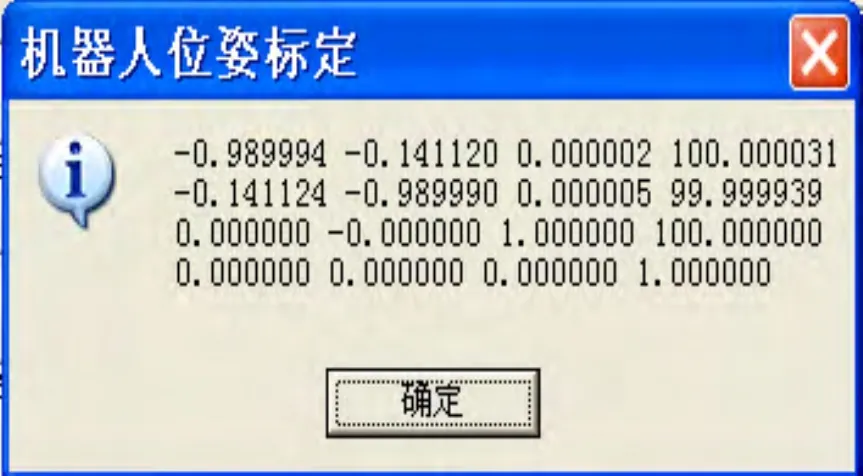
图5 外部位姿模拟的实验结果Fig.5 The experimental results of external pose simulation

从假设的真值式（23）与计算结果式（24）可以看出，其数据误差在10～5数量级上。 同理，若在数据不存在噪声因素的情况下，进行大量仿真实验进行推论，其系统精度级别高。

4 结论

本文建立双目立体视觉传感器三坐标的数学模型，得出空间特征点的三维坐标。通过机器人外部位姿工具与靶标法利用了机器人在某一静态位姿时的相关值进行了机器人在任意状态时都固定不变的机器人外部位姿的求解。仿真实验表明，在没有噪声因素的环境中，此方法可以获得机器人外部位姿的精确求解。

[1] 周富强.CCD摄像机快速标定技术[J].光学精密工程,2002, 8(1):97-99.

[2] 杨涛.基于合作靶标的激光扫描车身坐标测量关键技术研究[D]．天津:天津大学,2009:6-7.

[3] 杨剑,吕乃光.加权最小二乘算法在机器视觉系统中的应用[J].光学精密工程, 2009, 17(8):1871-1873.

[4] 王福斌,刘杰.挖掘机器人双目视觉系统标定方法与立体匹配[J].机械制造与自动化,2012,41(3) :157-160.

[5] Shiu Y C, Ahmad S. Calibration of wrist-mounted robotic sensors by solving homogeneous transform equations of the form AX= XB[J]. Robotics and Automation, IEEE Transactions on, 1989, 5(1): 16-29.

[6] 郑俊, 邾继贵.基于双目立体视觉的机器人测量技术研究[J].计量技术, 2005, 17(4):15-17.

[7] 郑俊.基于立体视觉的通用测量机器人标定模式研究[D]. 天津:天津大学,2005:25-29.