拓扑空间中的KKM型定理及其应用

王 彬

(内江师范学院数学与信息科学学院，四川，内江 641112)

0 引言

1929 年，B.Knaster，C.Kurnatoaski和S.Mazurkiewicz[1]在 n-维单形上证明了著名的KKM定理。KKM定理在非线性领域的研究中有着重要的应用。1961年，Ky Fan[2]将KKM定理推广到了无限维拓扑向量空间中并给出了 F-KKM 引理。 1968年，Browder[3]在KKM型定理的基础上建立了与集值映射相关的不动点定理，与集值映射相关的不动点定理在极大极小问题、截口问题以及社会经济平衡等问题中有着广泛的应用[4-11]。直到现在，对和KKM定理相关的非线性分析的研究成为数学和应用科学发展很快的一个领域。许多学者针对KKM引理中的凸性条件在不同结构的拓扑空间中（如：H-空间[12]、G-凸空间[13]、L-凸空间[14]和FC-空间[15]）对 KKM 定理及其应用的发展作出了重要贡献。其中这些拓扑空间都以前面的空间为特例，即G-凸空间以H-空间为特例；L-凸空间以H-空间和G-凸空间为特例，而FC-空间以H-空间、G-凸空间以及L-凸空间为特例。FC-空间要求从单形到拓扑空间存在一个连续映射。2011年，王彬[16]提出了具有性质(H)的无任何凸性和线性的拓扑空间，该空间削弱了FC-空间要求从单形到拓扑空间存在一个连续映射为单形到拓扑空间存在一个下半连续映射。本文利用具有性质(H)的拓扑空间中的一个新的KKM型定理，在具有性质(H)的拓扑空间中给出了匹配定理、极大元定理、不动点定理以及抽象经济的平衡存在定理。

1 预备知识

设X和Y是两个非空的集合，我们用〈X〉表示非空集合X的一切非空有限子集的簇；用2Y表示非空集合Y的所有子集的簇，对每个N∈〈X〉，表示N的基数，Δn表示以e0，e1,··,en为顶点的n维单形，用ΔJ表示顶点{ej:j∈J}的凸包，其中J为{0,1,···,n}的非空子集[11]。

我们记 C (X,Y)为从X到Y上的单值连续映射的集合。

定义1.1[16]称一个拓扑空间Y具有性质(H):若对每一个 N = { y0, y1, ··,yn} ∈〈Y 〉，均存在一个下半连续映射 φN:

定义 1.2[16]设X是具有性质(H)的拓扑空间，D是X的子集，称D是关于X的弱FC-子空间，若 对 任 意 N = { x0,x1, ··,xn}∈〈X 〉和 每 一{ xi0,xi1, ···,xik}⊂ N ∩ D ，有ψN( Δk) ⊂ N ∩ D 。

定义 1.3[16]设X是一非空集合，Y是具有性质(H)的拓扑空间。称映射 T : X → 2Y是广义R-KKM 映射，如果对任意 { x0,x1,···,xn}∈〈X〉，都 存 在 A = { y0,y1,··,yn}∈ 〈Y〉使 得 对 任 意{i0, i1, ···,ik} ⊂ { 0,1,···,n }有)。

引理 1.1[16]设X是非空集合，Y是具有性质(H)的拓扑空间， G : X → 2Y是一个闭值广义R-KKM 映射，则对任意 { x0,x1,··,xn}∈〈X〉，有(xi) ≠φ。

引理 1.2[16]设X是非空集合，Y是具有性质(H)的拓扑空间， T : X → 2Y是一个闭值广义R-KKM 映射，如果存在 M∈〈X〉 ，使得∩x∈MT(x) 是Y的紧子集，则

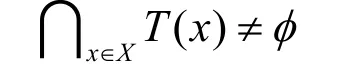
引理1.3[17]设X和Y是拓扑空间，S : X →2Y是非空集值映射，则下列条件等价：

(a) S有局部交性质；

(b) 对每一 y∈Y，存在X的开集Oy(可能是空的) 使得 O ⊂ S-1(y)且 X =；y

(c)存在映射 T : X →2Y使得对每一x∈X，T(x) ⊂ S(x) 且1(y)；

(e) S-1是转移开值的。

2 主要结果

定理2.1 设X是具有性质(H)的拓扑空间，D是X的非空子集，Y是拓扑空间，S:D → 2Y{∅} 是集值映射，且满足条件：

(1) S是开值的；

(2) 存在x0∈D使得Y S(x0)是紧的；

(3) S (D ) = Y 。

则对每一 f ∈ C (X,Y )存在 N = { x0, x1, ··,xn}∈〈D〉和( Δn) 使得(xi)。

证明 假设结论不成立，则存在一 f ∈C(X,Y )使得对每一 N = { x0, x1, ··,xn} ∈〈D〉， f(ψN( Δn))⊂Y。定义映射 G :D → 2 为 G (x) = Y S(x)，∀x∈D。则

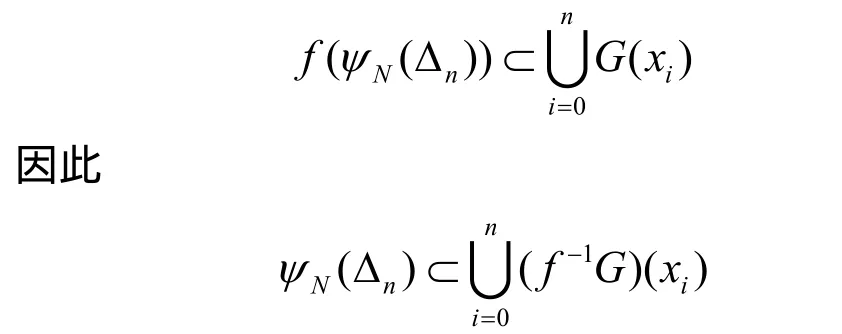
定义映射 F :D → 2X为 F (x) = ( f-1G)(x)，则ψN( Δn) ⊂ (xi)。因此，F是广义R-KKM 映射。

由(1)和 f的连续性，F是闭的。由(2) 和f的连续性，存在 x0∈D 使得 F(x0)是紧的。

由引理1.2， 可得

由此可得 S (D ) = ∪x∈DS(x) ≠Y ，这与条件(3)矛盾。

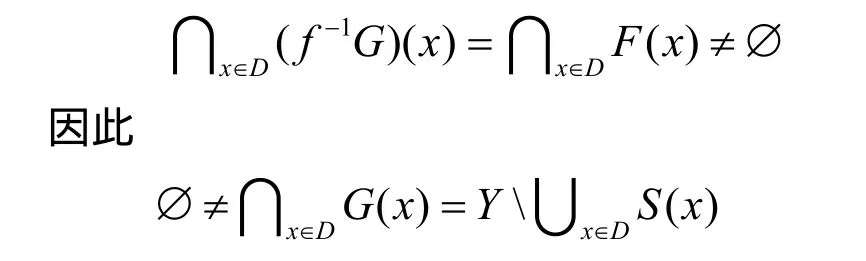
定理 2.2 设X是具有性质(H)的拓扑空间，D是X的非空子集，Y是拓扑空间，G :{∅} ，H :是集值映射，且满足条件：

(1)G是开值的；

(2)G(D ) = Y ；

(3)存在 x0∈D使得YG(x0)是紧的；

(4)对每一x∈D，G(x)⊂H(x)；

(5)对每一y∈Y，H-1(y)是弱FC-子空间。则对每一 f∈ C (X,Y )，存在X使得。

证明 由条件 (1)，(2)和(3)，根据定理2.1得，对每一 f ∈ C (X,Y )存在 N = { x0, x1, ··,xn}∈〈D 〉和( Δn)使得 。

定理2.3 设X是具有性质(H)的拓扑空间，集值映射 H :{∅} 满足条件：

(1)对每一x∈X，H(x)是弱FC-子空间；

(3)H满足引理1.3 (a)-(e) 条件中的一个。则H在X中有不动点。

证明 用 ( X,X,X,H-1)代替定理 2.2中的(X,D,Y,H ) ，并定义映射 T:为T(x) = int H-1(x)，∀x∈X，则对每一x∈X，

X T(x) ⊂ H-1(x) 且T是开值的。

此外，由条件 (3) 得 X = T (X)。不失一般性，假设对每一x∈X，T(x)≠∅ 。

又由条件 (1) ， (2) 和 f = IX，则由定理2.2得，存在X使得)，即)。

利用定理2.3的结果，可以得到一极大元存在定理。

定理 2.4 设X是具有性质(H)的拓扑空间，集值映射 H : X → 2X{∅} 满足条件：

(1) 对每一x∈X，H(x)=∅或 H(x)是弱FC-子空间；

(2)存在x∈X 使得 X H-1()是紧的；0

(3)H满足引理1.3 (a)-(e) 条件中的一个；

(4)对每一x∈X，x∉H(x)。则存在 x*∈ X 使得 H (x*)=∅。

证明 若对任意的x∈X，H(x)=∅，则结论显然成立。

假设对任意的x∈X，H(x)≠∅。则由条件(1)、(2)和(3)知满足定理2.3的条件，由定理2.3得，存在X使得，这与条件(4)矛盾。所以存在 x*∈ X 使得 H (x*)=∅。

作为定理2.3的应用，在具有性质(H)的拓扑空间中获得了对抽象经济和定性对策的平衡点存在定理。

设I是一个指标集， Γ = ( Xi; Ai, Bi; Pi)i∈I是一个有序四元组 (Xi; Ai, Bi; Pi)的族，其中对每一i∈I，Xi是非空拓扑空间 (策略集)，Xj→2Xi是约束映射，Pi: X → 2Xi是选择映射。一个点x称为抽象经济的平衡点，若对每一i∈I，且。

定理 2.5设X是具有性质(H)的拓扑空间A,B : X → 2X是两个约束映射， P : X → 2X是一个选择映射， Γ = ( X;A,B;P)是一个抽象经济和F : = { x ∈ X :(A ∩ P)(x) = ∅}满足条件：

(1)对每一x∈F，B(x)弱FC-子空间；

(2)对每一 x ∈ X F，(A ∩P)(x)弱FC-子空间；

(4)存 在 x0∈ X 使 得 X ((A-1()∩ P-1())∪(F∩B-1()))是紧的；

(5)对每一x ∈ X ，x∉( A∩P )(x)。则Γ在X中有平衡点。

证明 定义集值映射 T : X → 2X如下

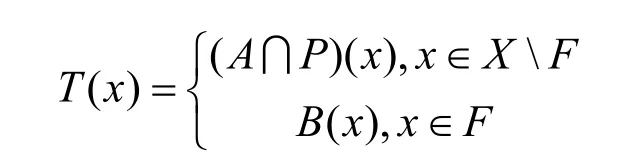
则由条件(1)和(2)，对每一xX∈，()Tx弱FC-子空间。由条件(3)，T满足引理1.3 (a)-(e) 条件中的一个。注意到对每一yX∈，

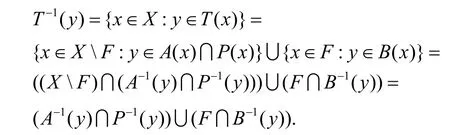
由条件(4) ，存在 x0∈ X 使得 Y T-1(x0)是紧的。由定理 2.3，存在使得)。但根据条件(5)。从而即，则(A ∩)=∅。因此是抽象经济Γ在X中的平衡点。

[1] Knaster B, Kuratowski C, Mazurkiewicz S. Ein Beweis des Fixpunktsatzes für n-dimensionale Simplexe[J].Fundamenta Mathematicae, 1929, 14(1): 132-137.

[2] Fan K. A generalization of Tychonoff's fixed point theorem[J]. Mathematische Annalen, 1961, 142(3):305-310.

[3] Browder F E. The fixed point theory of multi-valued mappings in topological vector spaces[J]. Mathematische Annalen, 1968, 177(4): 283-301.

[4] 孔德洲,丁协平.不动点和极大元定理在抽象经济中的应用[J].四川师范大学学报:自然科学版,2005,28(3):273-277．

[5] Zhang X. A generalization of Browders fixed point theorem with applications [J]. Nonlinear Analysis, 2007,67(11):3091-3097.

[6] 文开庭. μ0-超凸空间中的连续选择定理及其对抽象经济的应用[J].四川师范大学学报:自然科学版,2008,31（4）：397-401．

[7] Park S. On the von Neumann–Sion minimax theorem in KKM spaces [J]．Applied Mathematics Letters,2010,23（10）:1269-1273.

[8] 文开庭. 非紧完备 L-凸度量空间中的 GLSKKM 定理及其对抽象经济的应用[J].四川师范大学学报:自然科学版,2010,33(2):166-170.

[9] 王彬,龚小兵. FC-空间中的KKM型定理及其应用[J]．安徽师范大学学报:自然科学版,2011,34(4):314-316．

[10] Zhe Y,Yong J P. Generalized Browder-type fixed point theorem with strongly geodesic convexity on Hadamard manifolds with applications [J]．Indian Journal of Pure and Applied Mathematics, 2012,43(2):129-144.

[11] 王彬.拓扑空间中的截口定理及其应用[J].内江师范学院学报,2012,27(12):1-3．

[12] Horvath C D.Contractibility and general convexity[J].Journal of Mathematical Analysis and Applications,1991,156(2):341-357.

[13] Park S．Fixed points of admissible maps on generalized convex space[J]．Journal of the Mathematical Society of Korean,2000,37(4):885-899．

[14] Ding X P.Generalized L-KKM type theorems in L-convex spaces with applications[J].Computers &Mathematics with Applications,2002, 43(10): 1249-1256.

[15] Wang L, Ding X P.Fixed points,minimax inequalities and equilibria of noncompact abstract economies in FC-space[J].Nonlinear Analysis,2008,69(2):730-746.

[16] 王彬.拓扑空间中的KKM型定理及其应用[J].内江师范学院学报,2011,26(2):5-7．

[17] Ding X P. Coincidence theorems in topological spaces and their applications[J]. Applied Mathematics Letters,1999, 12(7): 99-105.