分裂节点法分析虚拟社会网络中的重叠社区

赵福明，盛桂珍，2

（1.长春工程学院，长春130021；2.吉林建筑大学城建学院，长春130111）

随着SNS网站的迅速发展和他们的用户数量成倍增加，虚拟社会的网络研究及其应用的重要性不容忽视。对于一个大型的、连接关系杂乱无章的虚拟社会网络，了解并分析其结构，将其分解成互相独立的集群是至关重要的。特别是，许多应用程序需要在理解抽象模型的组织结构的基础上，以推断其拓扑结构和它的元素之间的关系。这一研究也是信息流传播分析、推荐系统、虚拟社会影响最大化等的研究基础。

1 社会网络模型的介绍

在虚拟社区中，一个成员与多个主题的子社区相关联是非常常见的。由于一个人可以在现实世界中有多重身份，我们可以合理地假设：他／她可能分别加入了代表他／她的朋友、工作伙伴、家庭的子社区，或者他／她根据自己的多个兴趣参与了不同的组群。由此带来的问题是：一个社会网络里的各个集群可能或多或少地存在重叠。但是现有的大部分图聚类文献均没有考虑这样有重叠的社区。

图1展示了一个具有34个节点的典型重叠群落模型。在1区域和3区域的部分节点均与2区域内的节点有链接，但在1区域与2区域重叠，而3区域独立于2区域。即使不经过计算，我们也可以直观地看出1区域与2区域有更为紧密的联系，而3区域与后者的关联相对较弱。

定义1：在对整个网络进行划分之后，2个子群体含有相同的节点被称为重叠社区；2个子群不具有相同的节点，但在这2个子群中的节点有连接关系被称为分离社区；2个子群没有相同的节点且它们之间没有链接被称为无关社区。

定义2：在本文中，包括一个或多个重叠社区的社会网络分割的研究被称为有重叠社会网络分析。

根据上述2个定义，在有重叠的社会网络中，并非任意2个社区都必须是重叠的，也就是说，本文的研究并不强制2个子群具有相同的节点。这与图1所描述的网络结构相一致。

下面将阐述本文提出的有重叠社会网络模型的意义。首先，对于在重叠范围内的节点来说，它将与2个或以上不同社区里的节点有紧密联系。而由于这些被划分出来的社区不具有必要的或直接的关系，这意味着他们可能有不同的特点，例如社区内的成员会关注不同的主题或者是有不同的组织成员组成。在图1中，1区域中的节点28与2区域中的节点1都与重叠区域中的节点3相关联，然而节点28与节点3并没有直接的联系，暗示着2者可能存在不同的特点，而节点3将同时拥有这2种特性。这也就意味着重叠范围内的节点具有它所在的所有社区的特点，这与上文中提到的个体人类在现实世界中具有多重身份相吻合。其次，有重叠的社会网络分割更有助于社会网络分析的其他研究。对于单一节点，尤其是处于重叠区域的节点，我们可以更全面地了解它的特点及其与其他节点的连接关系。对于整个网络，直观来讲2个重叠社区间信息的传播会比2个分离社区更快更有影响，有重叠的社会网络研究将有助于我们对整个虚拟社会网络结构的理解和分析。

本文主要在现有研究的基础上，提出一个改进的数学模型及算法，以满足对社会网络分割提出的要求：适用于处理大型密集网络和海量数据，具有合理的运行效率，适用于已有的网络分割质量的评估系统。本文组织如下：第2节中我们给出分割节点法的基本模型及基础理论，以及其在其他数据模型中的适用性；第3节中我们将给出实验平台、实验数据的特点以帮助读者了解下一章；第4节给出我们实验中的细节、复杂度分析与实验结果；在最后一节中，我们提供了我们工作的潜在价值。

2 社会网络分析的基本概念

定义3：虚拟社会中某成员的好友，或在其抽象出来的无向图中与节点A有连接关系的点定义为A的邻接点。A的邻接点的集合V＝｛v1，v2…vn｝，我们定义为与A的子社区。

2.1 有重叠社区的数学模型

在具有现实意义中的重叠社区内，一个节点与其关联的子群的原始数学模型如图2（a）所示。然而，由于重叠区域内的点连接多个子社区，即A同时连接与其有关的4个集群，使得子社区之间并不相互独立，无法直接应用图的数据结构并实现遍历等算法，故这个模型并不方便做进一步的数据处理和结果评估。因此，我们将其转换成图2（b）的结构，也就是第1节中提到的分裂节点法。本文首先将A的邻接点按它们的连接紧密程度分成几个小组，如图2（a）中成员间具有紧密联系的大学同学、中学同学、同事与家人等。并根据这个分组将A赋予不同的编号。例如，对于连接A的高中同学而言将A标为A1，对于大学同学标为A2，家庭成员标为A3，同事标为A4。这样，A1、A2、A3、A4将被视为4个独立的节点参与后续的实验，而有重叠的社会网络模型也被转化为普通的网络结构。

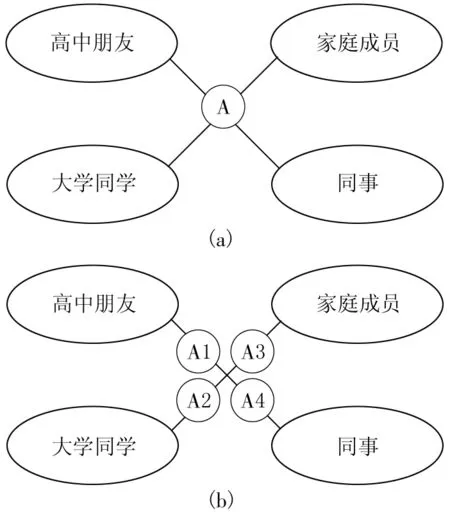
图2 现实中个体与相关群体的抽象模型及其变型

2.2 现有的研究成果

根据各社会网络的不同特性，研究人员一般选用谱分析方法、Kernighan－Lin算法、层次聚类算法这3种经典社会网络分析算法。虽然这些经典算法并不能直接应用于有重叠的社会网络分析，但他们对本文的研究有非常大的参考价值。

首次尝试研究有重叠的社会网络是2005年发表的［12］，并且他们提出了开放的CFinder算法（http：／／cfinder.org／）。CFinder提供了一个适用于各种研究领域的快速和有效的图分割方法，例如应用最为广泛的遗传网络和微阵列数据。然而，在分析如本文所选择的具有上亿个节点及百亿条连接的虚拟社会网络时，CFinder的运行时间和输出结果并不令人满意。

2.3 经典层次聚类算法

上一节中提到的3种方法在处理网络分割时的思想各不相同，本小节将详细描述本文实验将要用到的阶层式聚类算法，并且为了方便区分试验组与对照组，后文将称其为经典阶层式聚类算法。

这种方法的首要目标是度量在给定的网络结构内，任意有连接的节点（i，j）的相似性Xij，也就是人为的计算网络中所有连接的强弱程度。度量的方法之一是应用在各个图论领域的欧几里德距离：

其他的度量方法包括曼哈顿距离、最大传输距离和余弦相似度。本文中，我们将选取与余弦相似性类似的Jaccard相似系数来评价2个节点连接的紧密程度。在取得了两点的相似性之后，经典聚类方法指出根据网络的不同特点，我们可以用最短距离法或其他方法分离出各集群。在一般情况下，聚合式聚类算法的复杂度是O（n3）。

在本文中，我们将修改层次聚类方法，以降低其算法的复杂度，并使其适用于密集矩阵。在分割重复区域的节点时，我们将使用2.4节中介绍的功能函数作为分割算法的结束条件，而不是用经典分层聚类算法中提出的两集群的平均距离。并且为了与对照组比较，我们将分割过节点的数据与未处理的数据通过相同的程序处理，再利用功能函数评价网络划分的结果。

2.4 对分裂结果的评估

上一节提到的功能函数是数据挖掘领域中普遍承认的一种对网络划分的结果进行评价的方法：

式中：m为网络中原有的连接数；k为整个网络划分的集群的个数；li为第i个集群中的连接数，要求与该连接有关的2个节点都在第i个集群中；di为第i个集群中的节点数。

功能函数衡量了分割得到的子社区与相对应的随机社区在连接程度上的差异。随机社区在这里定义为与得到的第i个子社区有相同的节点数，但是节点之间有随机链接。对于分割完成的社会网络的Q值，如果大于0，这意味着分割的子社区有着比其随机社区节点之间更紧密的联系。反之，如果Q小于0，这意味着社区节点之间的连接比较松散，分割的结果并不理想。

虽然重叠的社区抽象模型是不同于一般的图结构，但我们将节点如图2（b）那样分割成互相独立的节点。因此，该函数仍可直接用于对本文算法的评估。

基于上述对功能函数的分析，我们可以定性地讨论有重叠的社区研究的优势。对比节点只能属于一个集群和节点可以出现在多个集群的数学模型，以下2种情况最有可能发生。其中一种是2个或2个以上的团体由于中间节点的连接而不能在社区划分的过程中被分离开。另一种是这个节点不会出现在所有与它有关的群体中。在这2种情况下，非重叠社会模型的功能函数中的di都将比又重叠的高，进而使得功能函数的结果降低。当然，第1种情况的发生对功能函数的结果影响更大一些。即使是在分裂节点后会使节点的数量增加，其影响力相比上文中的变化仍是微不足道的。4.3节2组实验的结果对比将证明上述分析。

3 实验准备及数据获得

本节将介绍实验的技术平台及数据特点，并将简单介绍数据预处理的方法及其必要性。

3.1 实验平台

本文主系统，包括网络机器人、节点相似度计算、节点分割与结果评估等，均由Java程序开发。主要是因为Java有丰富的处理网页内容和连接数据库库函数，并且非常适合于编写嵌套次数较多的循环函数。对于实验数据，已有的一些社会网络数据，如美国橄榄球俱乐部成员关系网络，和网络上的虚拟社会网络数据，如“脸书”上的好友关系，都是可用的。在本文的实验中，我们利用Http Client和HTMLParser从互联网上获得实验数据。另一个非常有用的工具是ODBC，是用于访问数据库管理系统（DBMS）的标准软件接口。

3.2 所选社会网络的特性

我们选择www.renren.com进行我们的研究主要是基于以下3个原因。1）它是一个实名的大学生交友网站，因此，我们不仅可以通过函数评估实验结果，也可以通过对现实中的成员关系的调研来评估。2）renren.com用户的连接图是一个典型的稠密矩阵。我们有2 095个成员节点和63 819个好友关系，虽然成员的ID仅有8～9位数字，但是数据占用75.3Mb的存储空间。在我们所研究的部分虚拟网络中，一个成员的好友数超过23人，就意味着其关系矩阵将是一个相对密集的大型矩阵。稀疏矩阵的特点是边数E≈节点数，N≈2个节点之间最短路径长度L。与稀疏矩阵相比，该矩阵具有边数E≫节点数N，以及2个节点之间最短路径长度L≪边数E的特点。因此，我们在下文中会重点讨论算法复杂度的问题。最后因为该网络中2个成员的好友关系是对等的，并没有指向性，所以该社会网络抽象模型是一个无向图，并且其关系矩阵是对称矩阵。这将大大简化实验需要考虑的问题，但是本文所提出的分割节点法同时适用于有向网络的分析。

定义4：实验中，数据准备的过程中获取过其所有好友关系的节点被称为准备好节点。若某节点的所有邻接点都是准备好节点，则这个节点称为一级节点。除一级节点之外的准备好节点称为二级节点。

在本次实验的数据中，我们选择10个一级节点，他们将是第4节实验过程中的论述重点。

4 实验过程

本节将给出实验过程及实现算法中的具体细节，并将重点分析节点相似度的计算方法、节点分裂数目、循环算法的边界条件等。

4.1 实验步骤

图3中，实线所标示的是分裂节点算法的实验流程，虚线是经典阶层式聚类算法实验步骤。经典阶层式聚类算法采用传统的无重叠的社会网络模型进行分析，并将作为本次实验的对照实验，以辅助对分裂算法的评估。评估将根据上文中提到的，以功能函数和基于事实的两种方法进行。

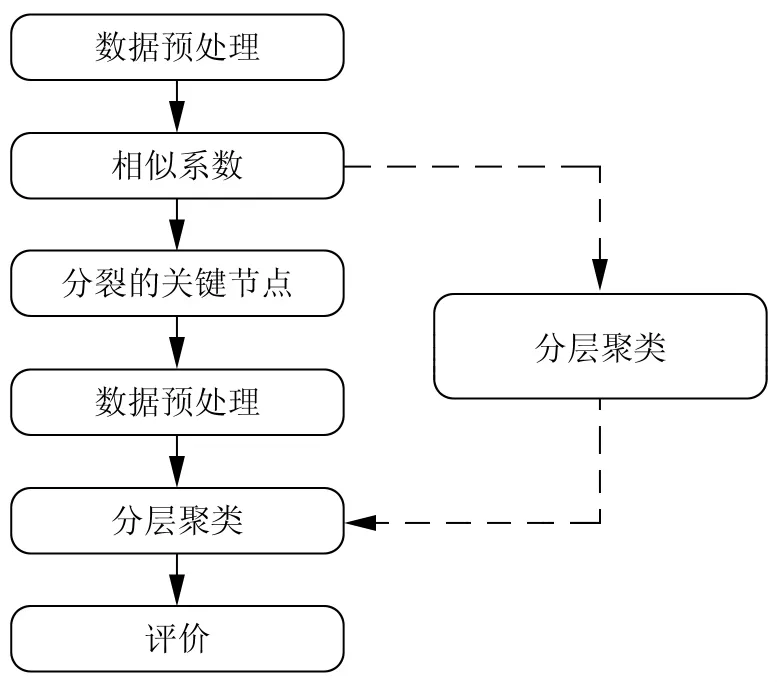
图3 实验流程图

4.2 根据相似度分裂一级节点

在本次实验中，将采用最常用的相似度算法之一，Jaccard相似度度量2个节点的紧密程度：

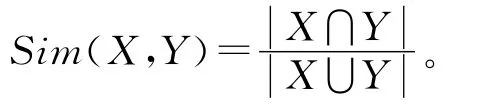
上述相似度计算公式最大的优势是相对较低的时间复杂度和空间复杂度。对于单一节点算法的时间复杂度和空间复杂度分别是O（n）和O（1），对于整个网络是O（n2）和O（n）。

除了采用较简单的相似度计算方法，将数据放在内存中，也可以在很大程度上提高计算速度。根据上述计算结果，我们删除图中最小相似度值的2个节点的连接，也就是删除虚拟社会网络中关系最不紧密的好友关系。

图4显示删除某一个一级节点的子社区中最低相似度的边，并将这个子社区分割为分立社区时，作用在其子社区上的功能函数的趋势图。

定义5：我们定义图4显示删除一级节点A的子社区中最低相似度的边并将这个子社区分割为分立社区时，作用在其子社区上的功能函数的曲线为A的Q曲线。

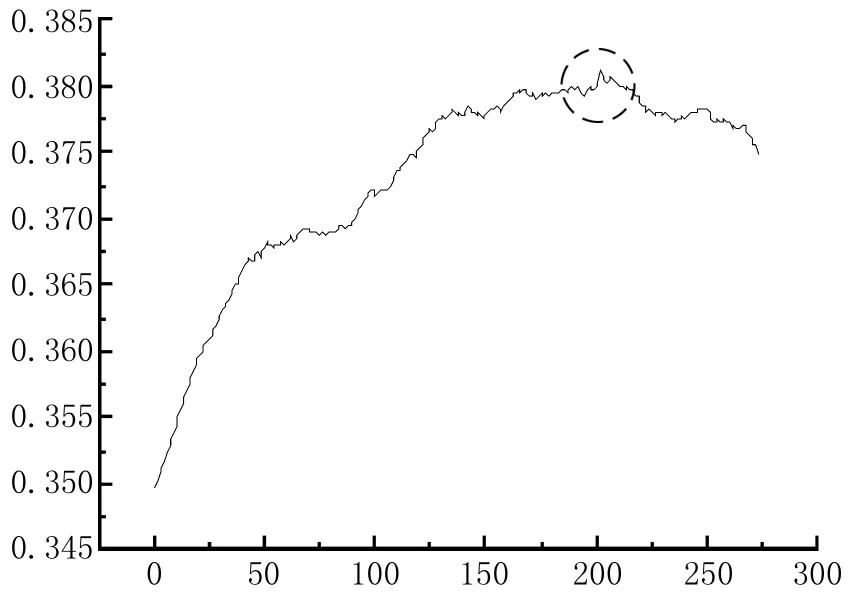
图4 1号节点的Q曲线

在大多数的一级节点，节点的Q曲线上与图4类似。整体来看该曲线像二次曲线那样上升和下降的过程，并有峰值。但与二次曲线不同的是，Q曲线并不是单调上升或下降的。在其上升或下降的过程中，也会出现很多小峰尖，一般出现在新的分立社区性成的时候。在这个实验中，当Q曲线达到最高点时我们停止删除边的循环算法，如图2所示。由于Q曲线并不是单调上升或下降的，故在循环程序运行到图中所示的功能函数最大值的时候，并不能直接判断是否已经到达最大值，我们需要继续运行程序，直到Q曲线衰减到一定程度时，本实验选取Q曲线已出现的最大值的0.8倍作为删除连接函数的截止条件。在图4中虚线所标记的Q曲线最大值处，该子图中的任意2个1号的邻接点的相似度最小值是0.091 65，最终1号节点的子社区分隔成3个分离社区，进而1号节点被分割为3个不同标记的节点。

4.3 2组实验的结果对比

图5中1线是所有一级节点经过分割处理后应用经典聚类方法对整个虚拟社会网络进行处理时功能函数的变化曲线，2线是一般的阶层式聚类算法对网络处理时函数的变化曲线。根据该图，我们可以看出应用分割节点法时的功能函数值大于经典聚类方法的功能函数值，在统计分析的意义上，分割的节点法得到比经典聚类方法更理想的结果。但由于在上图中2曲线有大致相同的变化速率，所以分裂节点的方法并不能加快处理的速度，也就是说，分裂节点法并不能提高得到最佳社会网络分割的算法效率，它只是优化了算法结果。

当我们应用分裂节点所得的结果进行实际情况抽样调查时，分割方法在分割节点时所得到的子社区分割结果也基本与事实相符。例如4.2节中提到的1号节点的子社区中，在这3个社区的成员大多分别是1号节点在小学、高中和大学的同学。

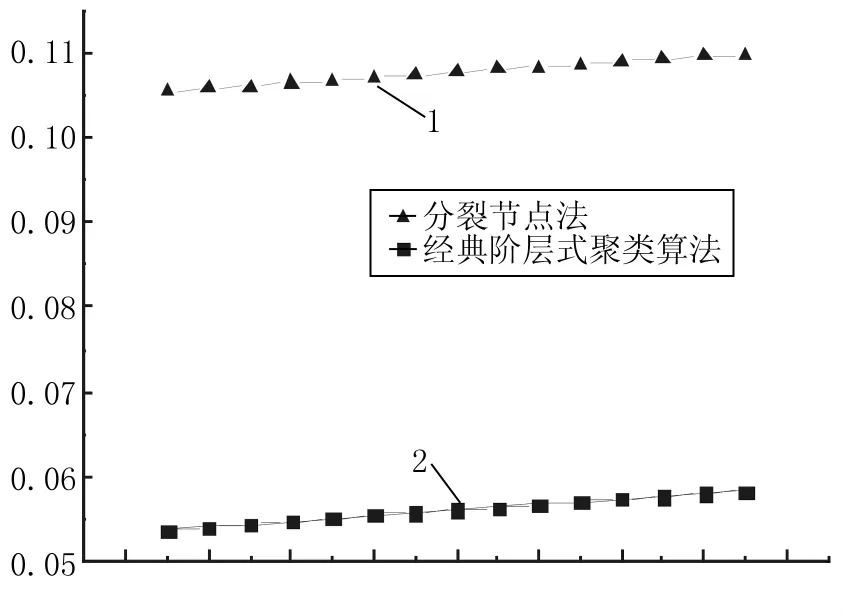
图5 应用分裂节点法（▲）与经典阶层式聚类算法（■）的功能函数变化曲线

［1］Duch J，Arenas A.Community detection in complex networks using extremely optimization［J］.Physical Review E，2005，72（2）.

［2］Flake G W，Lawrence S，Giles C L，et al.Self－organization and identi？cation of Web communities［J］.IEEE Computer，2002，35（2）：66－70.

［3］Baum’s J，Goldberg M.K，Krishnamoorthy M S，et al.Finding communities by clustering agraph into overlapping sub graphs［C］／／IADIS AC.IADIS，2005：97－104.

［4］Padrol－Sureda A，Perarnau－Llobet G，Pfeifle J，et al.Overlapping community search for social networks［C］／／Data Engineering（ICDE），2010IEEE 26th International Conference on.Long Beach，CA：IEEE，2010：992－995.

［5］Chung F.Spectral Graph Theory［M］.American Mathematical Society，1997.

［6］Newman M E J.Detecting community structure in networks［J］.The European Physical Journal B，2004，38（2）：321－330.

［7］Goldberg Mark，Kelley Stephen，Magdon－Ismail，et al.Finding overlapping communities in social networks［C］／／IEEE Second International Conference on Social Computing.IEEE，2010：104－113.

［8］Cazabet Remy，Amblard Frederic，Hanachi Chihab.Detection of overlapping communities in dynamical social networks［C］／／Social Computing （SocialCom），2010 IEEE Second International Conference on.IEEE，2010：309－314.

［10］Steve Gregory.An algorithm to find overlapping community structure in networks［C］／／Knowledge discovery in databases：PKDD 2007.Warsaw，Poland：Springer Berlin Heidelberg，2007：91－102.

［11］Jeffrey Baumes，Goldberg Mark，Magdon－Ismail Malik.Efficient identification of overlapping communities［C］／／Intelligence and Security Informatics.Atlanta，GA，USA：Springer Berlin Heidelberg，2005：27－36.

［12］王陆.虚拟学习社区社会网络中的凝聚子群［J］.中国电化教育.2009（8）：22－28.

［13］唐常杰，刘威，温粉莲，等.社会网络分析和社团信息挖掘的三项探索——挖掘虚拟社团的结构，核心和通信行为［J］.计算机应用，2006，26（9）：20－23.

［14］王陆.典型的社会网络分析软件工具及分析方法［J］.中国电化教育，2009（4）：95－100.

［15］石剑飞，闫怀志，牛占云.基于凝聚的层次聚类算法的改进［J］.北京理工大学学报，2008，28（1）：66－69.