部分和之和的弱不变原理

邹广玉

（长春工程学院理学院，长春130012）

0 引言

Arnold和Villasenor［1］在研究记录值分布时发现，有必要对“部分和之和”的极限行为进行研究。后来人们发现它在时间序列分析、随机游动和破产理论等领域中也有着广泛应用。例如，设｛Xt，t＝0，1，2，…｝为随机游动，记0，则St可表示第t日的某股票的收盘价，进而便是n日的移动平均线。鉴于“部分和之和”在理论和实际中的广泛应用，众多学者对其极限性质进行了深入研究，如文献［2］给出了独立同分布随机变量序列部分和之和的中心极限定理，其结果如下：

设｛Xn，n≥1｝为独立同分布随机变量列，满足记则

文献［3－4］研究了NA随机变量序列部分和之和的大数定律和中心极限定理，文献［5］讨论了独立同分布随机变量序列部分和之和的完全收敛性等等。周知，弱不变原理是概率极限理论中一类重要的结果，本文给出独立同分布随机变量序列部分和之和的弱不变原理。

定理1 设｛Xn，n≥1｝为独立同分布随机变量列，满足EX1＝01，记则

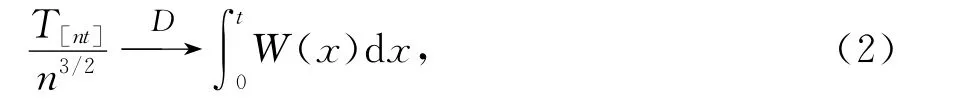
1 若干引理

引理1［6］（Kolmogorov不等式）设｛Xn，n ≥1｝为均值为0的独立同分布随机变量列，对于∀x＞0，有

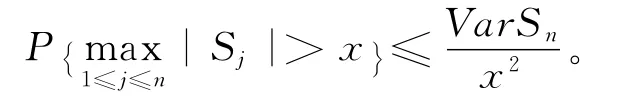
引理2［7］（连续映射定理）设h是距离空间S到S′的连续映射，｛Pn，P｝是S上的概率测度，则

其中“⇒”表示测度的弱收敛。

引理3［7］设S是一个距离空间，｛Xun，Xn｝是S×S上的随机元，如果对于固定的n→∞，和且对于∀ε＞0，

则

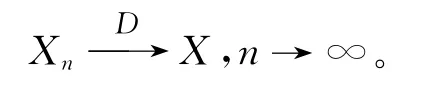
2 定理的证明

记

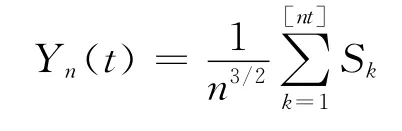
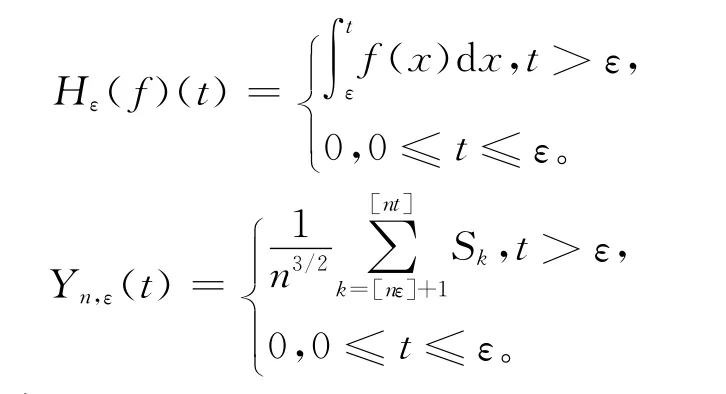
那么

由独立同分布序列的强大数定律，对于ε＞0一致地有

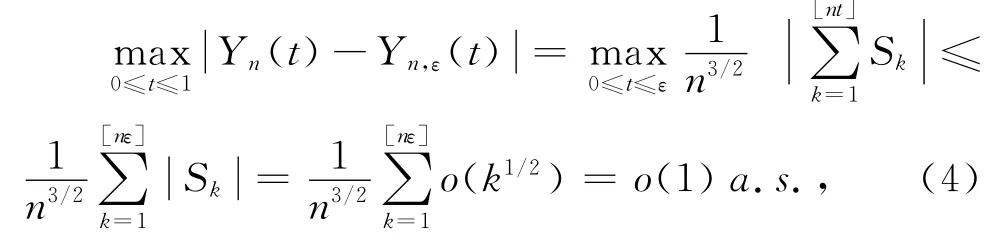
又

由引理1有

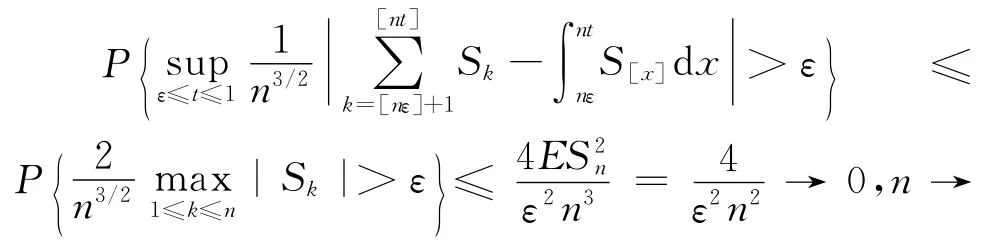
∞。于是对t∈ ［ε，1］一致地有

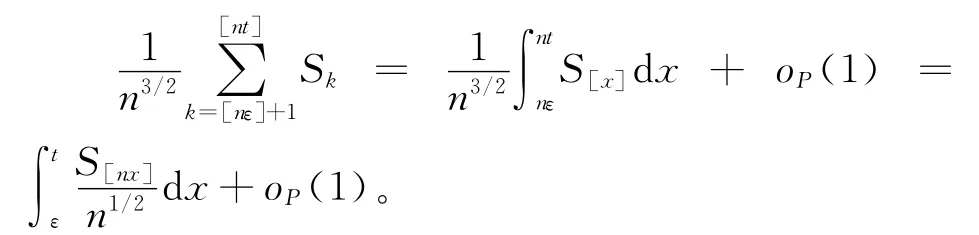
结合式（3）～ （5）并应用引理3便可得式（2）。

［1］Arnold B C，Villasenor J A.The Asymptotic Distributions of Sums of Records［J］.Extremes，1998，1（3）：351－363.

［2］江涛，林日其.I.I.D.随机变量部分和之和的极限定理［J］.淮南工业学院学报，2002，22（2）：73－75.

［3］宇世航.同分布NA序列部分和之和的强大数定律［J］.山东大学学报：理学版，2008，43（4）：62－66.

［4］宇世航，张锐梅.NA序列部分和之和的中心极限定理［J］.高师理科学刊，2007，27（3）：1－4.

［5］兰冲锋，吴群英.I.I.D序列部分和之和的完全收敛性探讨［J］.吉林大学学报：理学版，2012，50（3）：9－11.

［6］林正炎，白志东.概率不等式［M］.北京：科学出版社，2006：49.

［7］Billingsley P.Convergence of Probability Measures［M］.Second Edition.New York：Joh Wiley ＆ Sons，INC，1999.