加权距离判别法在膨胀土胀缩等级分类中的应用

宿晓萍，王亭亭，潘明远

（长春工程学院土木工程学院，长春130012）

0 引言

膨胀土在我国分布广泛，尤其是在河流流域地区分布更为集中。膨胀土主要由亲水矿物（主要是蒙脱石、伊利石和高岭石等）组成，具有吸水膨胀和失水收缩，并能反复胀缩变形的特性［1］。正是因为其胀缩性能，常常使得膨胀土地区出现房屋建筑物开裂，公路、铁路路基坍塌、失稳，膨胀土边坡产生浅滑等灾害［2］，给膨胀土地区的工程建设以及人民人身财产造成威胁。究其原因，是因为在工程勘察初期对膨胀土胀缩等级的错误判断［3］。因此，开展膨胀土胀缩等级分类的研究意义重大。

目前膨胀土分类的方法有很多，包括单指标评价方法（最大胀缩性指标分类法［4］、塑性图判别与分类法［4］和风干含水量法［5］等）和多指标综合评价法（灰色理论［6］、模糊数学［2］、可拓学［3］、支持向量机［1］、距离判别分析法［1］等）。影响膨胀土胀缩性的因素较多，单纯采用某一指标并不能如实反映区分开膨胀土的胀缩等级，多指标综合评判法近年来也被证明是提高评判膨胀土胀缩等级准确性的有效方法［7］。本文利用主成分分析法对距离判别模型加以改进，建立加权距离判别分析模型对膨胀土胀缩等级进行分类。结果表明该模型评判结果客观、准确。

1 主成分分析法

主成分分析法［8］是利用降维的思想，把多指标转化为几个综合指标的多元统计分析方法。该方法通过选取恰当的数学函数，使原变量成为新变量的线性组合，并选取在变差总信息量中比例较大的几个主成分来分析事物。主成分所占的变差信息量比例越大，那么在综合评价中所起的作用就越大。根据主成分分析的原理，确定膨胀土胀缩指标权重的基本步骤如下：

假设原变量指标为X1，X2，…，Xp，新变量指标为Z1，Z2，…，Zp，假设两者间存在线性相关关系，且可通过正交变换进行转换，即

其中矩阵C满足CC′＝I，其中Cij由下述原则确定：

1）Zi与Zj（i≠j）相互独立；

2）Z1是Zi中方差最大的变量，Z2次之，以此类推，Zp的方差最小。

Z1，Z2，…，Zp指标即为第1，第2，… 第p个主分量，方差依次递减。

由概率论可知，Zi与Zj相互独立的充要条件为cov（Zi，Zj）＝0，而Zi的方差 ＝cov（Zi，Zi），因此满足条件（1）和（2），即要求新变量Z1，Z2，…，Zp的协方差矩阵B ＝ （bij）p×p，即：

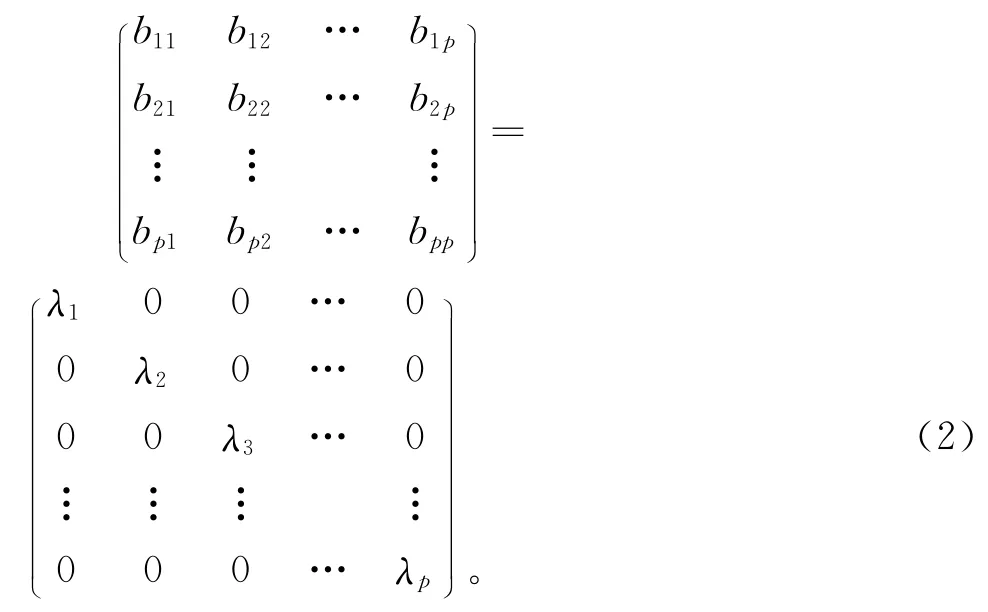
其中，λ1＞λ2＞ … ＞λp为原始指标X1，X2，…，Xp标准化后的相关矩阵R的特征根。

2 距离判别分析法

判别分析［9］是在已知样本数据和类别基础上建立判别准则，以此对未知待测样品类别进行分类判别的统计分析方法。目前在各领域内广泛应用。距离判别法为判别分析中的一种，其基本思想是：样本和哪个总体距离最近，就判定它属于哪个总体。

因距离判别法将所有指标重要性视为一致，而对于本次对象膨胀土胀缩等级，其影响因素的重要程度存在差异。因此本文选用加权距离判别法模型，使模型更客观真实。下面对模型进行介绍。

2.1 马氏距离

设膨胀土样本总体G ＝ ｛Y1，Y2，…，Ym｝T为m元总体，某一样本Y ＝ ｛y1，y2，…，ym｝T。利用上述主成分分析法确定泥膨胀土胀缩评价指标的权重W ＝ ｛w1，w2，…，wm｝，然后对原样本进行加权，可得新加权样本X＝WY。设μi＝E（μi）（i＝1，2，…，m），则总体均质向量μ ＝ ｛μ1，μ2，…，μm｝T。总体G ＝ ｛Y1，Y2，…，Ym｝T的协方差矩阵为

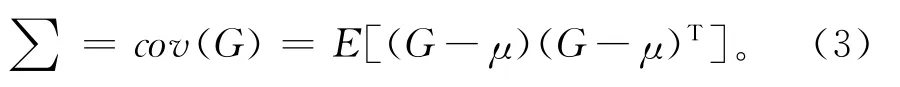
那么，样本X与总体G的马氏距离为：

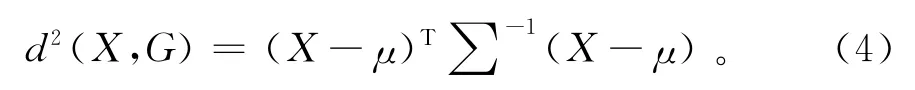
2.2 2个总体的距离判别

假设有2个加权总体G1和G2，其中总体Gi（i＝1，2）的训练样本为1，2；t＝1，2，…，ni），其中，ni指总体Gi的样本个数，则μi的估计量为

总体Gi的协方差矩阵∑i的估计为组内协方差矩阵Si，如式（6）和式（7）所示。

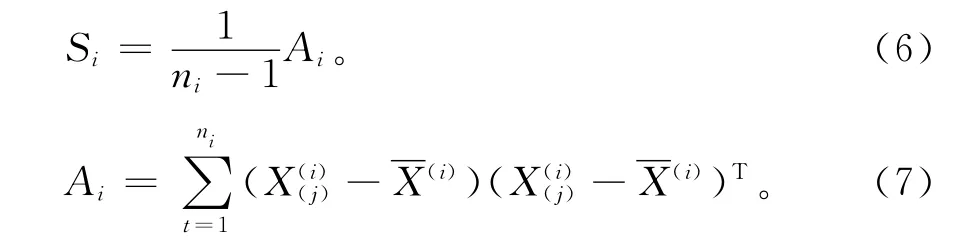
当∑1＝∑2＝∑，协方差矩阵∑的无偏估计为

当∑1＝∑2时，对待判样本X的判别可基于分别计算样本X到2个总体G1和G2的马氏距离，按照最近准则进行判别。马氏距离简化后的计算公式如下：

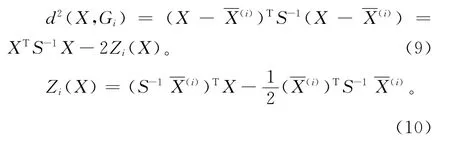
其中i＝1，2。将待判样本X 代入上述公式算得Zi（X），再按式（11）所示判别准则即可进行分类：

2.3 多个总体的距离判别

假设有k个m 元总体：G1，G2，…，Gk，判定任意给定样本X＝ （x1，x2，…，xm）T属于哪个总体，可按照马氏距离最近准则进行判别，分别计算各样本X到k个总体的马氏距离，并把X判为距离最小总体，如式（12）所示：

本文计算马氏距离时，是通过训练样本的统计量作为μi和∑i来进行计算。

2.4 判别准则的检验

对于判别准则的优良性，一般采用交叉确认估计法［10］来计算误判率。

以2个总体G1和G2为例，假设两总体中分别有n1和n2个样品。交叉确定估计法在每次建立新的判别准则之前将剔除掉训练样本中的1个，以剩余的n1＋n2－1个训练样本来建立新的判别准则，以此判别剩余的样本，并将误判的比例作为误判概率的估计。误判率η的计算公式如下：

式中：n12为将G1中的样本误判为G2中的个数；n21为将总体G2中的样本误判为G1中的个数。

3 模型应用

3.1 判别指标的选取

影响膨胀土胀缩性的指标主要有2类：土的物质组成指标（黏土矿物组成及粒度组成等）和土的水理性质指标（液限、塑限、塑性指数、自由膨胀率等）。在前人研究基础上，本文选取黏粒含量（x1），粉粒含量（x2），液限（x3），塑限（x4）及塑性指数（x5），作为判别指标。

3.2 加权距离判别模型的建立

选用文献［11］中安康膨胀土为实例，选取其中16个样本数据（见表1）作为训练样本进行学习，其余7个作为待判样本进行检验。选取黏粒含量、粉粒含量、液限、塑限及塑性指数作为分类指标，将膨胀土划分为强膨胀土（A）、中等膨胀土（B）以及弱膨胀土（C）3类。首先通过主成分分析法确定出各指标的权重分别为W＝｛0.226，0.169，0.213，0.185，0.207｝，然后按照上节介绍的加权距离判别模型建立判别函数。计算判别函数即可完成对样本的判别。

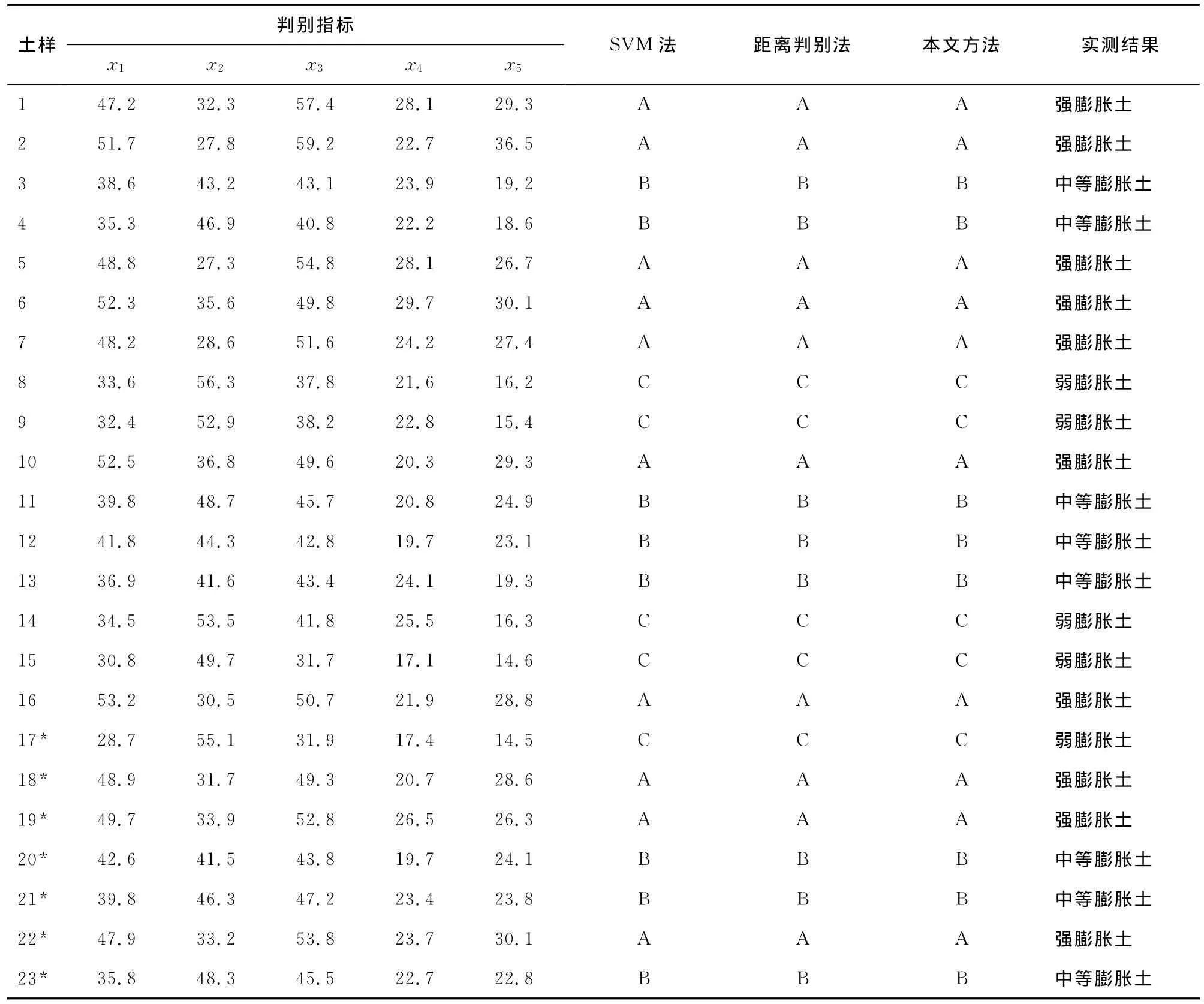
表1 加权距离判别法分类结果与实际结果对比

3.3 模型检验

为了检验模型判别结果的可靠性，本文选用交叉确认估计法来计算误判率。利用学习好的加权距离判别模型对剩余7个样本进行判别，判别结果与实测结果一致（见表1），说明误判率为0%，模型可靠。同时，本文将模型评价结果与支持向量机（SVM）模型［1］和距离判别分析模型［10］的评价结果作比较，三者评价结果一致。由此说明，加权距离模型在膨胀土胀缩等级分类中完全可行和高效。

4 结语

1）膨胀土胀缩性受多指标综合影响，不同指标对其膨胀性影响又有所不同。本文选用黏粒含量、粒含量、液限、塑限及塑性指数作为判别指标，利用主成分分析法确定各指标权重大小，并建立加权距离判别分析模型进行判别，判别结果合理可靠，较为真实地反映了各指标对膨胀土膨胀性的影响以及膨胀土的膨胀性。

2）加权距离判别法在本次评判中与距离判别法结果一致，但其考虑了各指标权重，更加客观、科学。当样本数多时，其判别准确率将可能优于距离判别法。该方法计算简单高效，为膨胀土等级分类提供了一种新的方法。

［1］马文涛.支持向量机在膨胀土分类中的应用［J］.岩土力学，2005，26（11）：1790－1792.

［2］黄卫，钟理，钱振东.路基膨胀土胀缩等级的模糊评判［J］.岩土工程学报，1999，21（4）：408－413.

［3］汪明武，金菊良，李丽.可拓学在膨胀土胀缩等级评判中的应用［J］.岩土工程学报，2003，25（6）：754－757.

［4］刘特洪.工程建设中的膨胀土问题［M］.北京：中国建筑工业出版社，1997.

［5］谭罗荣，张梅英，邵梧敏，等.风干含水量 W65用作膨胀土判别分类指标的可行性研究［J］.工程地质学报，1994，2（1）：15－26.

［6］李玉花，冯晓腊，严应征.灰色聚类法在膨胀土分类中的应用［J］.岩土力学，2003，24（2）：304－306.

［7］傅鹤林，范臻辉，刘玉琛.利用人工神经网络模型判定膨胀土等级［J］.中国铁路科学，2002，23（5）：118－120.

［8］罗志忠，张丰焰.主成分分析法在公路网节点重要度指标权重分析中的应用［J］.交通运输系统工程与信息，2005（6）：78－81.

［9］范金城，梅长林.数据分析［M］.北京：科学出版社，2002.

［10］宫凤强，李夕兵.距离判别分析法在岩体质量等级分类中的应用［J］.岩石力学与工程学报，2007，26（1）：190－194.

［11］易顺民，晏同珍.膨胀土判别与分类的人工神经网络方法［J］.地质科技情报，1995，14（3）：91－94.