基于Ansoft的圆筒式永磁调速器传动特性影响因素分析

方 军，陶红艳，余成波

(重庆理工大学 a.机械工程学院;b.远程测试与控制技术研究所，重庆 400054)

近年来，磁性材料性能的提高及其广泛应用使得磁力传动技术发展迅速［1］。永磁调速器作为一种磁力传动装置，通过磁场相互耦合来传递扭矩，消除了电机与负载之间的刚性连接［2－4］，在电力、石油化工、水处理等领域中已经有所应用［5－7］。但是，由于它引进国内时间不长，对其研究很有限。国内外研究主要集中在气隙圆盘式调速器的结构设计和特性分析方面［8－9］，对于改变耦合面积的圆筒式研究相对较少［10］。在永磁调速器中使用了价格昂贵的金属，如铜和高磁能积的永磁材料，导致其成本相对较高，故有必要对其结构尺寸进行设计优化，在保证承载能力的情况下减小体积、节约材料、增加传递扭矩［11］。本文以圆筒式永磁调速器为研究对象，介绍其结构与工作原理，建立有限元数学模型，根据扭矩表达式找出影响传动特性的因素，选定主要因素，运用Ansoft对每个因素进行变化的三维瞬态仿真，得到各因素对扭矩的影响曲线，分析变化原因，得出结论，可为圆筒式永磁调速器结构尺寸设计优化、电机转速和导体材料选择提供依据。

1 结构与工作原理

1.1 机械与主磁路结构

图1为圆筒式永磁调速器机械结构简图，其主要由3部分构成:①与输入轴相连的导体转子，包括高导电率的导体、导体轭铁以及机械连接部分;②与调速机构连接的永磁转子，由磁体轭铁及其上径向充磁交错布置的永磁体组成;③调速机构部分，可使永磁转子轴向移动，调节两转子耦合面积。导体转子和永磁转子之间无机械连接。

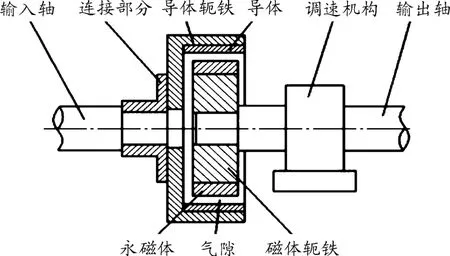
图1 圆筒式永磁调速器结构简图

圆筒式永磁调速器磁路复杂，其主磁路可简化为图2。磁转子上永磁体径向充磁，N、S磁极交错布置，磁通从磁极N出发，经径向通过两转子之间气隙和对应的导体部分，后沿轴向经过导体轭铁，再沿径向经导体和气隙回到相邻S极，在磁体轭铁上闭合形成回路。

图2 圆筒式永磁调速器主磁路

1.2 调速器工作原理

调速器安装在电机与负载之间，设备启动前调速过程见图3(a)，先调节调速机构使两转子耦合面积为零，电机带动导体转子以ω1运转，由于耦合面积为零，导体转子没有切割永磁转子磁力线，不产生感应磁场，无扭矩传递，永磁转子处于静止状态。电机稳定运转后，调节调速机构使两转子耦合面积改变，见图3(b)。耦合面积改变使两转子通过磁场相互作用产生的扭矩变化，磁体转子转速改变。稳定运转时，两转子存在转差ωs。当装置安装在系统时(如图4所示)，控制器部分可以接收传感器采集的过程信号(流量、压力、液位等)，通过与设定的值进行比较，经处理后发送给气隙调节器，通过气隙调节器调节气隙，改变转速，满足负载部分的转速要求。

图3 启动调速过程

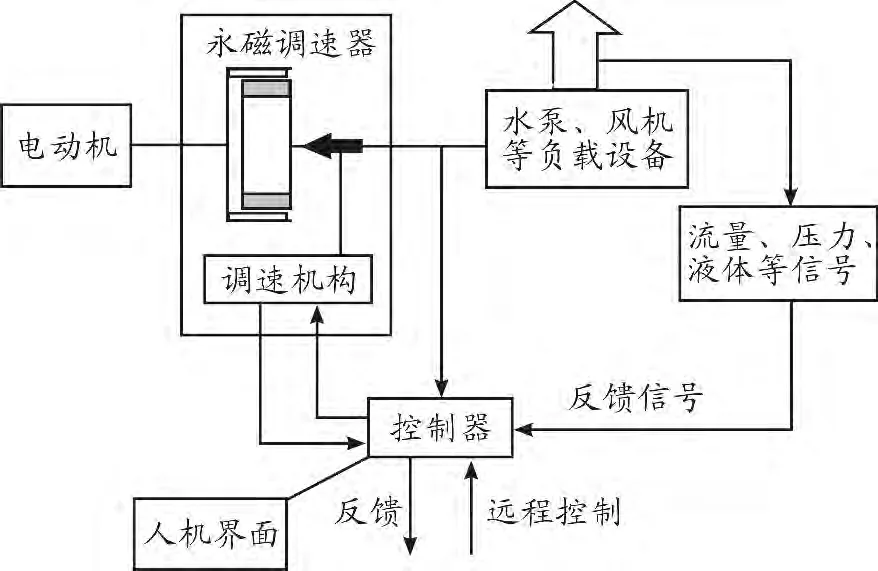
图4 永磁调速器系统使用原理

2 数学模型

为了分析方便，对模型和材料属性做简化和假定:模型几何尺寸在运动方向上不变。材料各向同性，铁磁材料磁导率按B－H曲线确定。不考虑温度对电导率和磁体性能的影响。只考虑模型中与磁性有关的部件，忽略模型两端机械结构的影响。

在计算区域中不存在静止的电荷，电磁场Maxwell微分方程组可简化为［12］

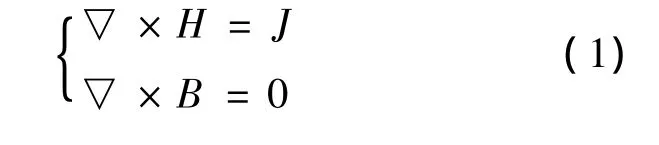
附加方程为

式中:H为磁场强度(A/m);J为传导电流密度(A/m2);B为磁感应强度(T);σ为电导率(S/m);μ为磁导率(H/m);E为电场强度(V/m)。

引入矢量磁位A，磁感应强度B可表示为

由式(1)～(3)得

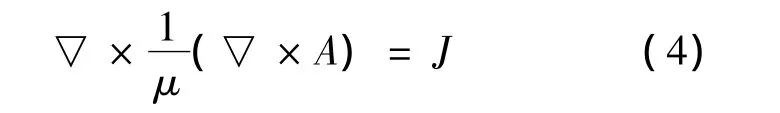
按照洛伦茨规范，标量电位φ为［13］

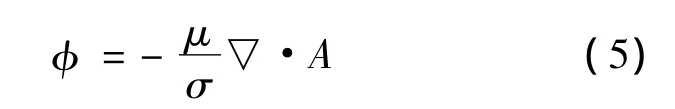
考虑导体的运动，求解区域电流密度为［13］:

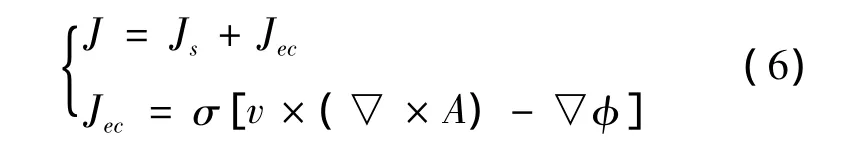
式中:Js为源电流密度(A/m2);Jec为涡流电密度(A/m2);v为导体运动速度(m/s)。

求解区域被分成导体涡流区V1、磁体区V2、其他区V3。各区域的控制方程如下［14］:

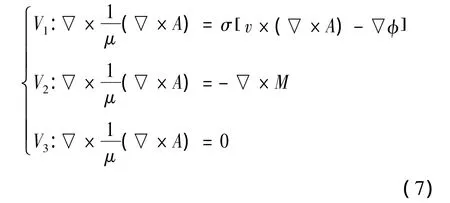
式中M为磁体磁化矢量。

由控制方程组可知:导体的运动速度v是常数且方程中没有关于时间t的导数，因此三维运动涡流场是稳态场。利用磁矢位A和标量电位Φ求解区域内的磁感应强度B、电流密度J后即可得到转矩 T［15］

式中:V为涡流区域体积;r约为导体内半径。

由式(8)知:转矩T与导体内半径r、传导电流密度J、磁感应强度B、涡流区域体积V有关，其中J为涡流电密度。由式(6)可知:涡流电密度与转差、导体电导率有关;磁感应强度B与磁体径向长度、磁极数、气隙径向长度、转差有关;涡流区域体积V与导体轴向长度、转差有关。随着轴向长度增加涡流区域体积也会增大。转差会影响涡流强度、集肤效应。转矩影响因素众多，可对每一因素进行分析。

3 模型建立与仿真参数设定

在Ansoft中定义设计参数，建立模型。模型结构尺寸见表1。模型最外层为计算区域，可通过改变区域尺寸多次仿真。当2次仿真结果相差在5%内时，认为计算区域尺寸合理［16］。设定材料参数见表2，磁材料依据图2中N、S交错进行径向充磁。分别设定各部分的网格大小，建立扭矩参数，设定涡流效应区域，添加分析尺寸参数变化范围及步长。有限元仿真模型如图5所示。

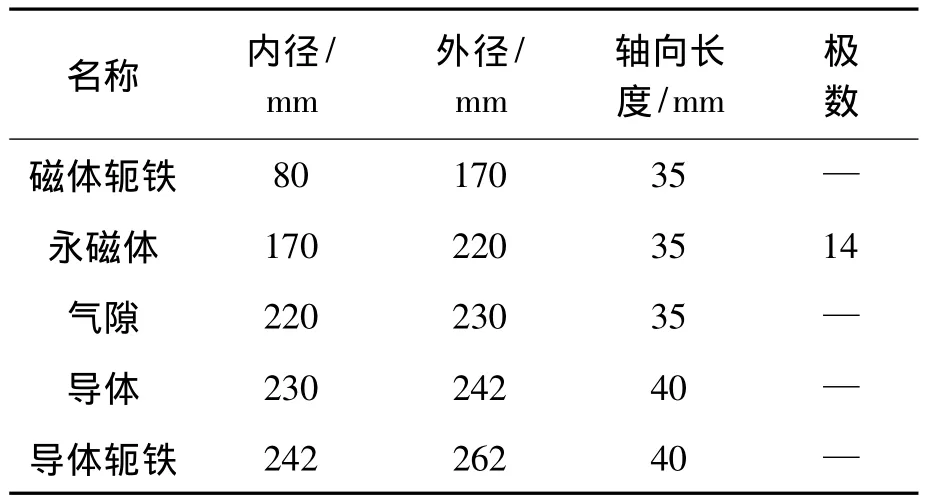
表1 模型结构尺寸

表2 材料参数

图5 仿真模型

4 转矩影响因素分析

4.1 磁场分析

永磁调速器是通过磁场相互作用传递扭矩，扭矩与气隙磁感应强度B大小有直接关系。在静态时，气隙磁场由永磁体提供，在一定转差时，气隙磁场由永磁体磁场与涡流磁场叠加形成。图6为静态时导体内表面中点处磁感应强度矢量图。图7为转差在500 r/min时导体内表面中点处磁感应强度矢量图。静态时最大磁感应强度为0.93 T，瞬态时最大磁感应强度为1.045 7 T，大小和方向都发生了改变。气隙磁场分布和大小受磁体结构尺寸、气隙导体尺寸、转差等综合因素影响。

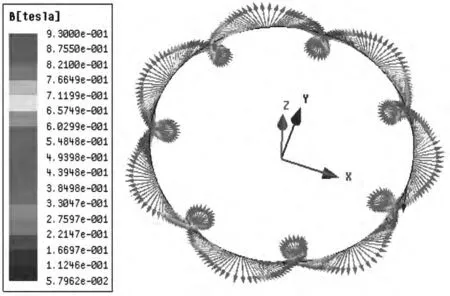
图6 静态气隙磁感应强度矢量图

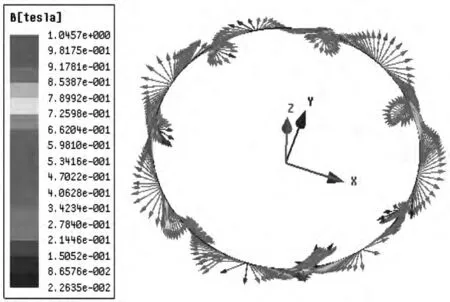
图7 动态气隙磁感应强度矢量图

4.2 转矩与各因素关系

在其他因素不变的情况下，保持两转子转差为500 r/min，单独改变一个影响因素，取仿真稳定后转矩平均值作转矩与该因素的关系曲线，分析转矩随影响因素的变化情况。同时，为了提高单位体积的材料(永磁体、导体)所产生的扭矩大小，了解材料利用情况，引入扭矩与材料体积比参数ψ(每m3材料对应扭矩大小)来考察材料性能是否得到充分利用。

磁体极数与扭矩、磁材料参数ψ之间的关系见图8。由图可知:磁极数从2～12对变化时，转矩先增加后减小，在5对时转矩最大，参数ψ与扭矩变化相似。磁极数对转矩影响较大，N、S磁极每变化一次，静磁能存储一次，磁极增加有利于静磁能的存储，静磁能会影响转矩大小［14］。在极数增加到一定时，磁极间接触总面积增大，漏磁增加，有效磁势、气隙磁通密度减小，转矩降低。磁材料参数ψ反映了磁能的利用率。在设计时，极数为偶数，应选较大的参数ψ，以便有效利用磁能。同时，还要考虑加工装配情况。在一定外径尺寸下，磁体极数较少时，磁块较大，可能制造不便，磁体极数较多时，装配较麻烦。

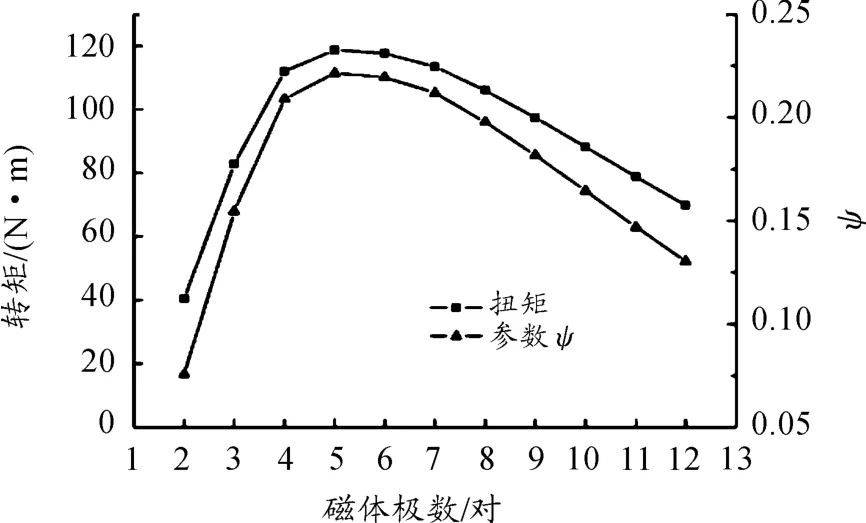
图8 磁体极数与转矩、参数ψ关系曲线

磁体内径与转矩、磁材料参数ψ之间的关系见图9。当内径在60～140 mm变化时，转矩和参数ψ近似直线增加。由式(9)知:磁体内径增加会使导体内半径r增大，转矩增大，同时磁能利用率也提高。所以，在径向设计尺寸允许下选择大半径的磁体轭铁有利于提高转矩。

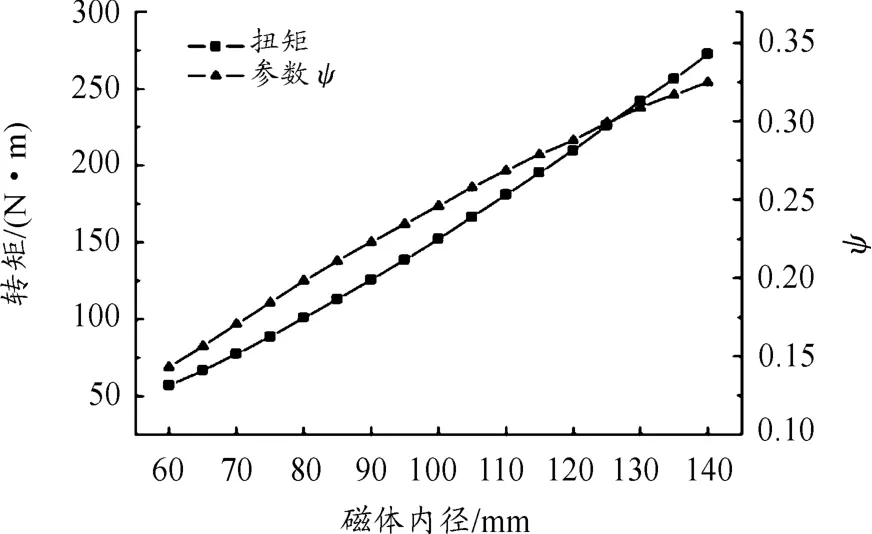
图9 磁体内径与转矩、参数ψ关系曲线

磁体径向长度与转矩、磁材料参数ψ之间的关系见图10。径向长度在5～70 mm变化时，转矩几乎呈直线增加。但参数ψ减小较快，即磁能利用率降低明显。这是因为磁体体积增加量与磁体径向长度的平方成正比，而转矩增加较慢。在设计时应综合考虑两者，在满足扭矩设计的情况下保持较大的ψ值。

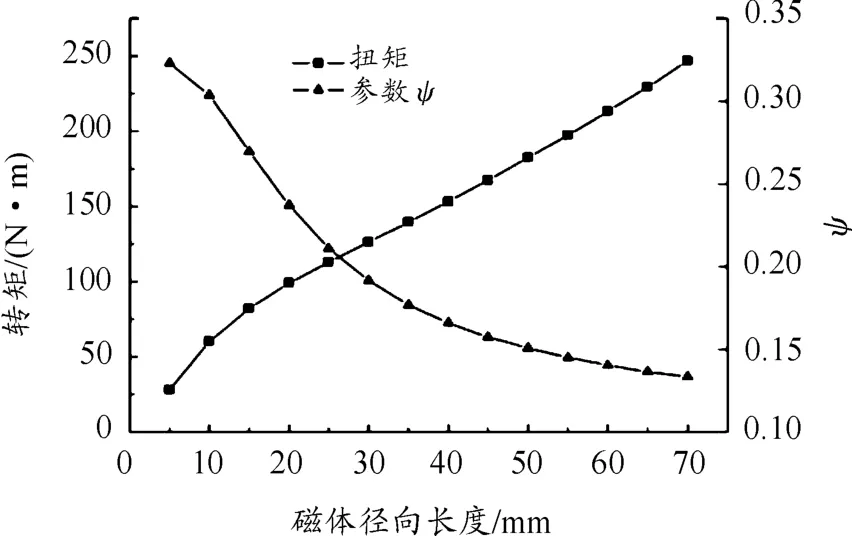
图10 磁体径向长度与转矩、参数ψ关系曲线

磁体轴向长度与转矩、磁材料参数ψ之间的关系见图11。在轴向长度在10～90 mm变化时，转矩近似线性增加，而磁材料参数ψ先增加较快，后变缓。磁体轴向长度的变化反映调速时传动转矩的变化情况。由于调速是通过改变两转子耦合面积来实现，轴向长度增加相当于耦合面积增大，因此可以通过适当增加轴向长度来提高扭矩，但在一定长度后磁能利用率增加变缓。在设计时应选择合适的长度，同时，由于转子一般为悬伸结构，轴向长度设计还要考虑调速机构行程、连接轴的强度刚度、轴向安装空间等情况。

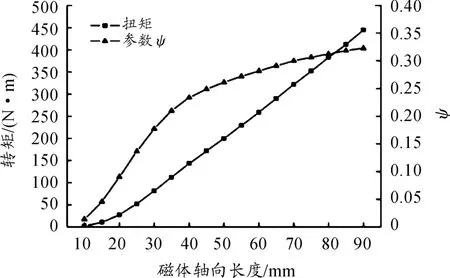
图11 磁体轴向长度与转矩、参数ψ关系曲线

导体径向长度与转矩、导体材料参数ψ之间的关系见图12。随着导体径向长度的增加，转矩先增加后减小，在约4 mm时转矩达到最大，参数ψ随导体径向长度增加而降低。由于导体影响涡流形成，进而影响转矩。涡流有集肤效应，磁场变化角速度越快，涡流渗入深度就越小。在转差一定时，渗入深度一定，当导体厚度小于此渗入深度时，涡流形成少，不利于转矩产生，所以随着厚度的增加转矩增大。但在厚度增加到一定时，导体轭铁与磁体间距增加，使得垂直穿过导体的磁感线减少，有效磁场减小，转矩降低。导体一般用贵金属制造，选择合理径向长度有利于降低调速器成本。在设计时导体径向长度应大于常用调速范围内的最大涡流渗入深度，同时由于涡流产生热量，在导体径向尺寸较小时，需要进行温度校核。

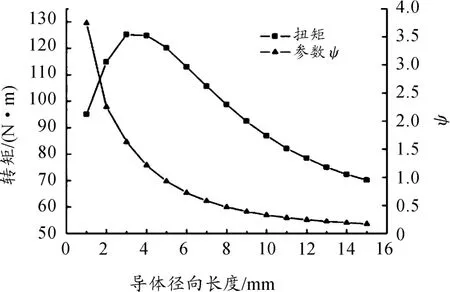
图12 导体径向长度与转矩、参数ψ关系曲线

气隙径向长度与转矩、磁材料参数ψ之间的关系见图13。随着气隙径向长度的增加，转矩和参数ψ都减小较快。气隙磁导率低，当厚度增大时消耗的磁势增加，导致气隙磁通密度减小，有效磁能利用率降低，转矩降低。应选择较小的气隙尺寸，以便有效利用磁能。同时，由于转子的悬伸结构和在调速过程中两转子有相对轴向移动，因此需要考虑加工、装配能达到的同轴精度，以及运转过程中的振动、散热情况。

导体电导率与转矩的关系见图14。电导率在1×106～7×106S/m变化时，转矩先增加，后增加变缓。电导率增加，涡流密度增大，转矩增加，当增加到一定时，涡流密度趋于饱和。导体使用的材料通常有铜、铝等，在表1模型尺寸和转差500 r/min的条件下，铜导体产生的扭矩为113.03 N·m，铝导体为101.34 N·m。导体材料选择应考虑性价比，大多情况下选电导率较高的铜材质。

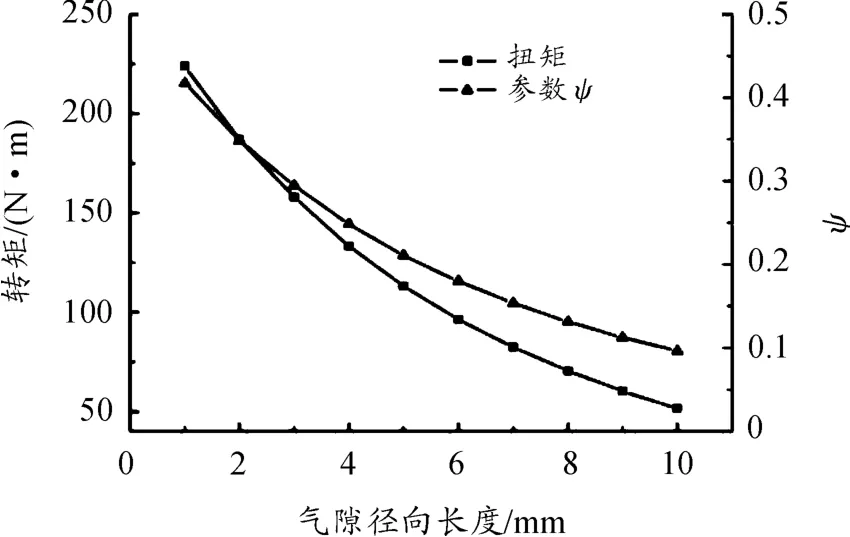
图13 气隙径向长度与转矩、参数ψ关系曲线

图14 转矩与导体电导率关系曲线

两转子转差与转矩的关系见图15。若结构参数不变，转差在0～1 000 r/min变化时，转矩先增加后减小。由式(6)知:涡流密度与转差成正比，转差增大，导体转子涡流密度增加。低速时，由于涡流密度较小，涡流产生的反磁场小，磁势与磁通变化不大，转矩随转差的增加而增大。在转差进一步增大时，涡流效应逐渐明显，总磁势与磁通减小，转矩减小。在转差从0到最大扭矩时的转差调速范围内，涡流损失小，效率较高，可根据此曲线的输出转矩和负载转速选择相应的电机转速［17］。

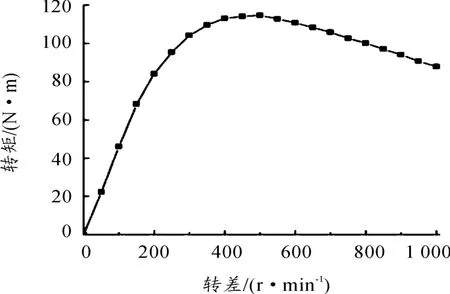
图15 转矩与转差关系曲线

5 结束语

圆筒式永磁调速器传动特性影响因素众多，通过对主要因素进行三维瞬态分析，获得了各因素对转矩影响的变化规律曲线，同时考察关键材料的利用率。研究结论可为该类调速器的结构优化设计提供参考。

1)随着磁体极数的增加，转矩先增加后减小。磁极按偶数配置，一般少于20极，应选择磁能利用率较大时磁极数;随着磁体径向厚度的增加，转矩呈线性增加，但是，磁能的利用率下降;在径向设计尺寸允许的条件下可以适当增大磁体轭铁直径，以获得较大扭矩，提高磁能利用率;轴向长度的增加有利于磁能利用率的提高，但磁能利用率的增加会逐渐变缓。

2)随着导体径向长度的增加，转矩先增加后减小。在设计时应使导体径向长度大于常用调速范围内的最大涡流渗入深度;在导体径向长度较小时，需要对导体进行温度校核，可采取冷却措施，降低导体上的温度;在兼顾生产成本的基础上应选用电导率较高的铜材质。

3)气隙径向长度对转矩影响较大，随着气隙径向长度的增加，转矩和磁能利用率减小较快。在考虑加工和装配可以达到的同轴精度，以及振动散热等情况下应选择较小气隙，以便有效利用磁能，获得较大转矩。

4)随着转差的增加，转矩先增加后减小。从转差0到最大扭矩时转差范围内的传动效率较高，电机转速可根据转差和转矩的关系曲线以及调速范围来选择。

［1］胡文艳.钕铁硼永磁材料的性能及研究进展［J］.现代电子技术，2012，35(2):151－152.

［2］刘应诚.永磁磁力传动原理及应用［J］.通用机械，2012(3):98－101.

［3］MOHAMMADI S，MIRSALIM M，VAEZ Z S，etal.Analytical Modeling and Analysis of Axial－Flux Interior Permanent－Magnet Couplers［J］.Industrial Electronics，IEEE Transactions on，2014，61(11):5940－5947.

［4］SHIN H J，CHOI J Y，JANG S M，et al.Design and Analysis of Axial Permanent Magnet Couplings Based on 3D FEM［J］.IEEE Transactions on Magnetics，2013，49(7):3985－3988.

［5］高庆坤，印胜伟.永磁调速技术在电厂锅炉吸风机中的应用［J］.中国设备工程，2014(6):38－39.

［6］易轶虎.永磁调速技术在炼油企业的应用与前景分析［J］.石油石化节能与减排，2013，3(4):25－28.

［7］王洪滨，刘文华，杜江，等.永磁调速节能技术在大功率循环水泵上的应用［J］.节能技术，2014(2):178－181.

［8］张泽东.永磁磁力耦合器设计与关键技术研究［D］.沈阳:沈阳工业大学，2012.

［9］MOHAMMADI S，MIRSALIM M，VAEZ Z S，et al.Sensitivity analysis and prototyping of a surface-mounted permanent-magnet axial-flux coupler［C］//Power Electronics，Drive Systems and Technologies Conference(PEDSTC)，2014 5th.［S.l.］:IEEE，2014:568－573.

［10］徐伟，孙建军.永磁调速器的涡流场分析［J］.机械传动，2015，39(2):115－118.

［11］赵清，邵龙，于静泽，等.变速磁力耦合器研究［J］.电气应用，2013，20(4):82－87.

［12］杨超君，郑武，李直腾，等.可调速异步盘式磁力联轴器性能参数计算［J］.中国机械工程，2011，22(5):604－607.

［13］刘伟，佟强，杨帛润，等.永磁调速器的有限元分析与性能计算［J］.微特电机，2015，43(4):10－13.

［14］王旭，王大志，刘震，等.永磁调速器的涡流场分析与性能计算［J］.仪器仪表学报，2012，33(1):55－60.

［15］赵博，张洪亮.Ansoft12在工程电磁场中的应用［M］.北京:中国水利水电出版社，2010:303－325.

［16］何富君，仲于海，张子华，等.抽油机永磁耦合驱动研究［J］.石油机械，2014，42(10):60－64.

［17］杨超君，郑武，李志宝.可调速异步盘式磁力联轴器的转矩计算及其影响因素分析［J］.电机与控制学报，2012，16(1):85－91.