应用多目标规划的马赛克自动铺贴设备成本优化研究

李 正，范彦斌，张宪民

(1.华南理工大学，广州 510641;2.佛山科学技术学院，广东 佛山 528000)

马赛克生产属于以传统手工制作为主体的劳动密集型产业。目前存在生产标准不完善、无序竞争激烈、公司之间仿冒抄袭严重等缺陷，技术研发得不到足够重视，相关技术进展缓慢［1］。马赛克颗粒的铺贴作为马赛克生产流程的重要环节，是决定马赛克生产效率的瓶颈环节，其效率和质量直接影响到产能与产品质量。然而传统的铺贴工艺主要通过人工逐片逐点实施，不仅效率低下，而且影响人体健康［2］。因此，马赛克全自动铺贴生产线的设计和研发成为提高产能、实现清洁生产的重要途径。

马赛克的铺贴对设备精度要求较高，同时由于市场需求的多元化，对设备的灵活性和适应性［3］也有一定的要求，即既可以进行单一品种大批量生产，又可以进行多品种小批量生产。设计自动铺贴设备需要合理的结构和布局，均衡设备的成本和效能。国外对马赛克的设计与生产早有研究。Oral等［4］设计了一种4自由度的机械手进行大理石马赛克的铺贴，但铺贴机械手的制造成本较高。Cayiroglu等［5］开发了玻璃马赛克铺贴的生产线，但只能实现逐行铺贴，生产效率无法满足大订单、大批量生产的市场需求。

目前国内生产玻璃马赛克产品的企业以中小型居多，在设备方面的投入有限。国产的马赛克自动铺贴设备精度较低，其中效率较高的只能铺贴单色［6］或双色马赛克［7］，能铺贴三色或者三色以上马赛克的设备则具有生产效率低、设备成本高的缺点［8］。王永翔等［9］设计的彩色图案马赛克铺贴设备的铺贴机构采用机械手逐个铺贴方式，工作效率低，成本高，设备的竞争力不强。

设备制造成本的优化是产品设计的重要环节。于洋等［10］针对某电子产品生产线的单元生产转化建立了操作工人数和产品流通时间的多目标优化模型。其他一些关于成本优化的研究多以遗传算法为主，求解车间布局和装配线序列等问题［11－13］，但其优化目标与本文的研究有所不同。柴月珍［14］从物流成本优化的角度出发，建立了混合整数线性模型。马翠等［15］针对建筑外表面光伏电池铺设问题建立了优先级选择模型。傅晨曦等［16］利用设备系统的历史故障记录建立了神经网络模型，预估各个分系统使用寿命对产品工艺参数的影响，通过遗传算法确定总成本最低的预防性维护周期优化方案。

本文参考正在研发中的多色复杂图案马赛克自动铺贴设备，基于其流水线结构和自身特效对制造成本和生产效率的影响，建立了多目标优化模型。在不消耗物理制造资源的前提下，对于缩减设计和制造周期、进行辅助生产线的设计和改进具有重要作用。

1 自动铺贴设备工作原理

工厂在产品生产过程中，会依照客户要求，按既定颜色配比和阵列顺序先将23 mm×23 mm×8 mm的玻璃马赛克颗粒铺入尺寸为298 mm×298 mm、间距为2 mm的模板中，见图1。该工序称为铺贴。每块模板共可铺贴12×12(即144)颗玻璃马赛克颗粒。

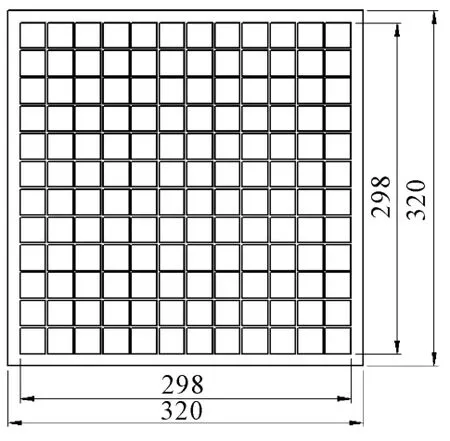
图1 马赛克模板规格

流水线基本结构包括由模板供料系统、模板运输系统、马赛克颗粒供料系统和铺贴系统组成的工作站。生产线节拍P为模板在某一工作站完成该站的铺贴过程后再运送至下一工作站所消耗的时间。当模板通过所有工作站时会被铺满与预设方案相同的多色马赛克颗粒阵列。

假设流水线供料与铺贴机构由N1个工作站组成，由图2可知工作站在流水线两侧对称分布，每两个工作站构成一个工位。令整条流水线有N2个工位，则有

马赛克颗粒铺贴系统采用的铺贴机构为吸盘组，组数为3时的结构简图见图3。每一组吸盘数量为12，吸盘间距与模板中的马赛克颗粒相同。

若对规格为12×12的模板进行n种颜色的马赛克铺贴，令每个工作站铺贴机构吸盘组的排数为x，则整套流水线需要的工作站数N1=n·

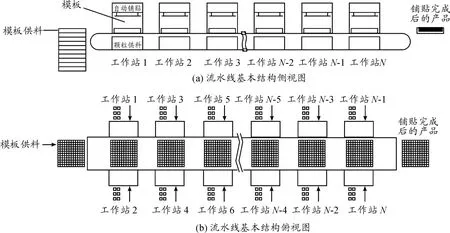
图2 流水线基本结构

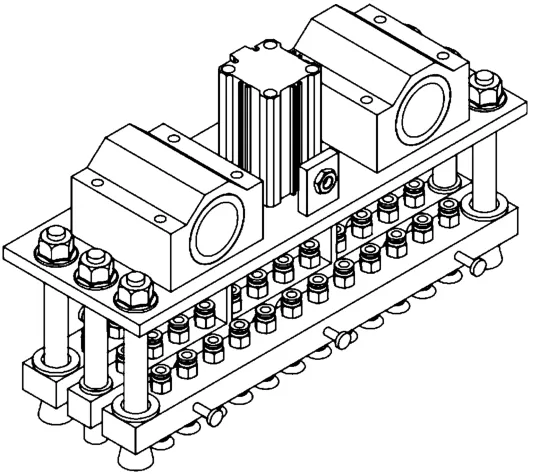
图3 铺贴机构结构简图(组数为3)

流水线的全部气动系统由PLC控制，每个吸盘的吸气都是相互独立的，即每个吸盘占用1个I/O量。每个工作站安装有2个气缸，分别执行吸盘组在流水线流动方向和垂直流动方向的动作，即每个工作站占用2个I/O量。每个工位需要1个气缸驱动流水线上运输的模板定位装置，同时需要1个光电传感器检测流水线上模板的位置，即每个工位需要占用2个I/O量。因此，整套设备需要占用的I/O量为(12x+2)N1+2N2。

2 数学模型

2.1 模型描述

已知每一盘(12×12)三色马赛克颗粒可获利a元。依据马赛克铺贴所需颜色种类数为n，马赛克模板规格为12×12，目标产量(盘)为m，生产线节拍为P，每个PLC的最大点数为k，控制每个工作站吸盘组的排数为x，应使得完成铺贴指标消耗的时间T尽量短，同时尽量减少设备制造的成本S。

2.2 问题分析

总耗时T构成包括正常生产耗时和停机维护耗时。总成本S构成如下:

1)生产线机架采购、加工、装配成本;

2)工位数变更影响生产线总长度导致的机加工成本;

3)工位数变更影响电控系统总I/O量数导致的PLC采购和安装成本;

4)吸盘组铺贴机构加工成本;

5)设备故障维护成本(非零件损耗，因为零部件损耗周期过长)。

因此，得到目标函数为:

minT=T1+T2

minS=S1+S2+S3+S4+S5

s.t.

x=1，2，…，12

n为大于1的整数

m为大于400的整数

3 设备故障概率估计

本文设备在按时检修和保养的前提下，受供电电压、真空泵提供气压不稳定等不确定因素的影响，在铺贴玻璃马赛克颗粒时会有一颗或几颗颗粒落出模板外，影响模板在传送带上的运输(即出现卡盘现象)，从而导致临时停机和维护。

假定本设备单个工位连续铺贴马赛克时出现卡盘现象是完全随机的，并假定铺贴任一模板时出现卡盘的机会均相同。实测得到100次卡盘故障记录。在故障出现时立即停机，同时记录下已完成铺贴的模板数(合格品)，结果见表1。

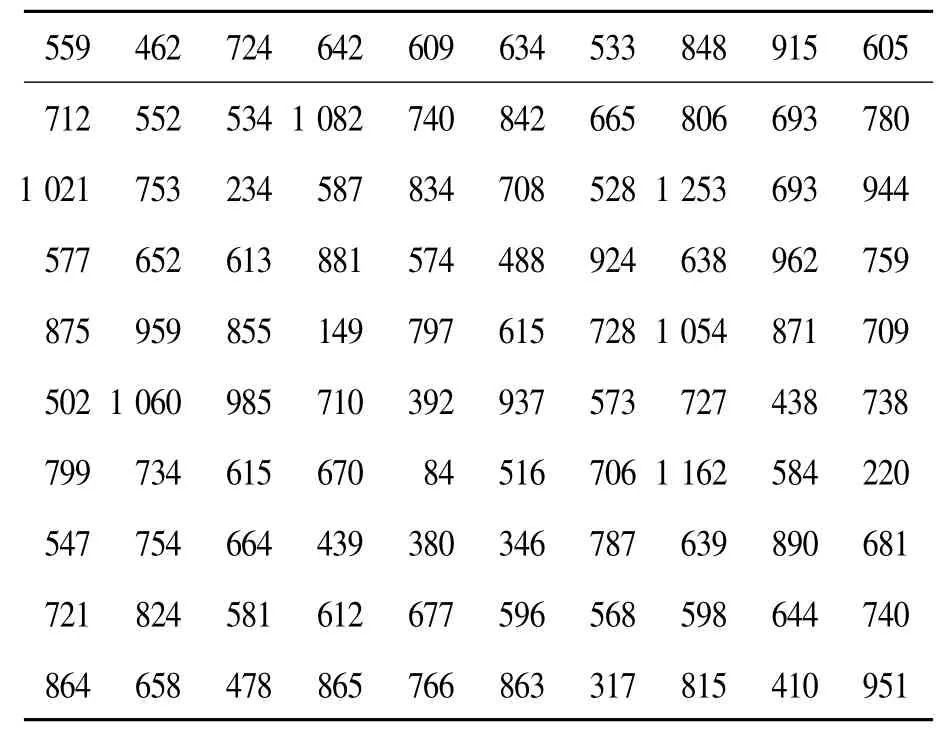
表1 100次卡盘故障记录

数据输入:

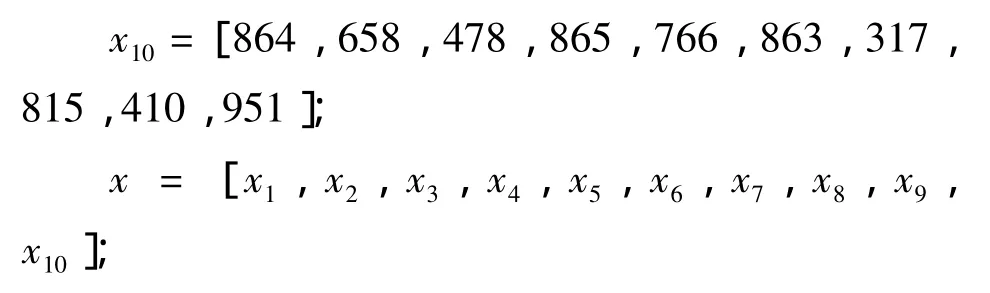
卡盘次数频数直方图见图4。.

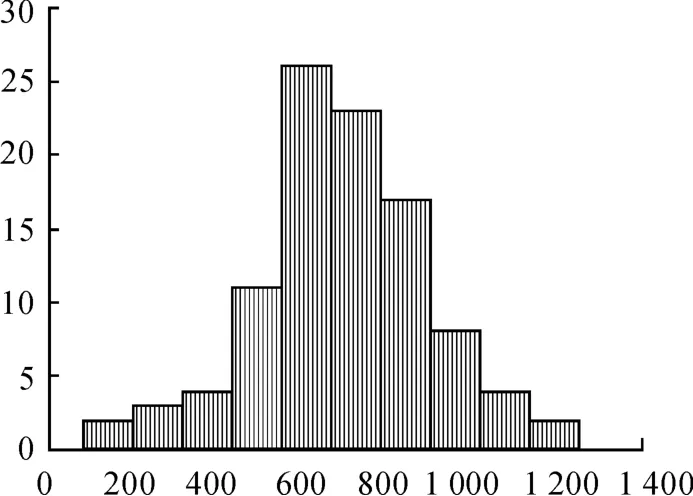
图4 卡盘次数频数直方图

进行分布的正态性检验［17］，得到正态概率图，如图5所示。

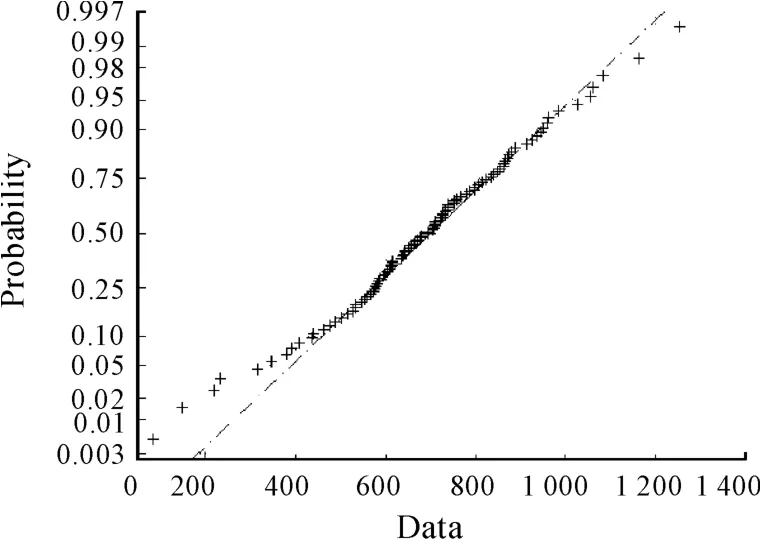
图5 正态概率图

参数估计:

［muhat，sigmahat，muci，sigmaci］=normfit(x);

计算结果:

muhat=690.04，sigmahat=208.223 3，muci=［648.724 0，731.356 0］，sigmaci=［182.821 5，241.887 9］

由此估算出该设备出现卡盘次数的均值为690，标准差为208，均值的 0.95置信区间为［648.724 0，731.356 0］，标准差的0.95 置信区间为［182.821 5，241.887 9］。

假设检验

［h，sig，ci］=ttest(x，690);

检验结果为:

1)布尔变量h=0，表示不拒绝零假设，说明提出的假设卡盘次数均值690是合理的。

2)95%的置信区间为［648.724 0，731.356 0］，完全包括690，且精度较高。

3)sig 的值为0.998 5，远高于 0.5，不能拒绝零假设。

因此，可认为单个工作站平均每铺贴690次会出现1次卡盘现象。

卡盘的概率可估计为1/690。在多工位的情况下，各个工作站出现卡盘现象属于相互独立事件，即设备出现卡盘现象的工作站个数N服从二项分布B(N，1/690)。计算设备工作时发生1次卡盘事件的工作站个数X的期望为E(x)=N1/690。对一个工作站进行临时维护耗时15 min，需支付维护费30元，故进行一次维护的时间成本的期望为Te=15E(x)/60，资金成本期望为Fe=30E(x)。

4 模型计算和分析

4.1 生产耗时计算

假设每次卡盘故障排除后生产流程重新开始。生产线节拍由2个步骤构成:模板运输和吸盘铺贴，分别耗时6 s和5 s，即 P=6+5=11 s。根据工位个数，可计算正常生产耗时 T1。

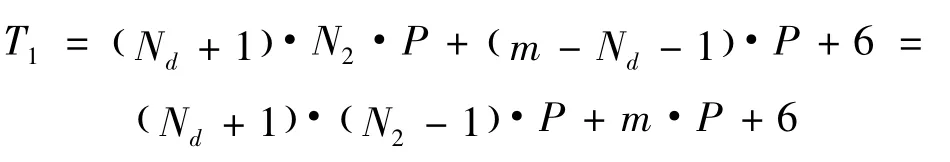
4.2 设备制造成本计算

生产线机架采购、加工、装配成本S1为定量，S1=30 000元。每个工作站的制造成本 F1=25 000元，每增加一个工位导致生产线长度增加而产生的机加工成本F2=3 000元，故总成本S2=N1·F1+N2·F2=25 000N1+3 000N2。

设备采用的PLC最大I/O点数k=128，单价F3=3 000元。每个吸盘对应1个开关量，每个工作站有2个驱动气缸占用2个开关量，每一个工位需要1个定位气缸和1个光电传感器占用2个开关量，即每个工作站需要占用的PLC采购成本为

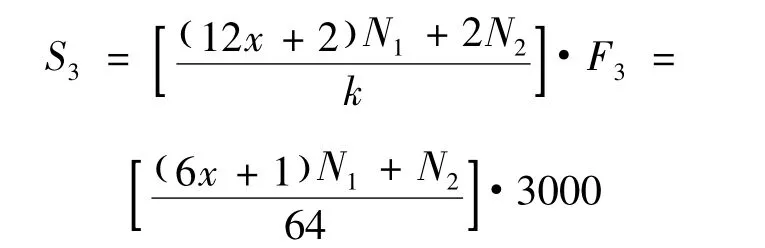
单个工作站吸盘组铺贴机构加工成本为

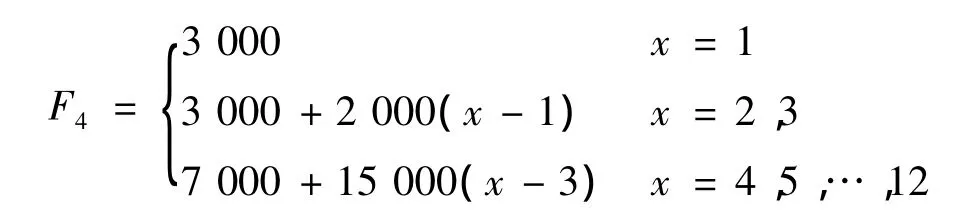
则整条流水线吸盘铺贴机构所占用的成本为

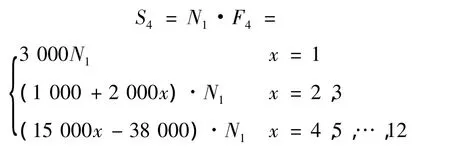
综上，可得模型如下:

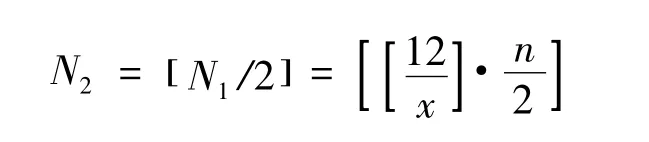
M=10 000时，x与总成本的散点图见图6。

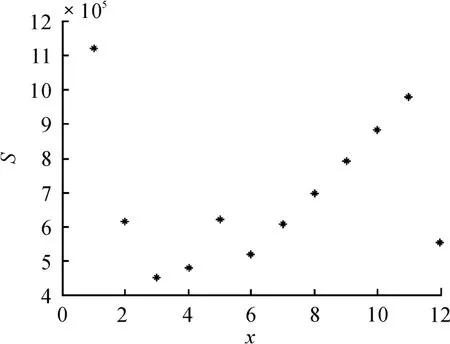
图6 单个工作站吸盘组数x与制造点成本S的散点图

x与生产总耗时的折线图见图7。

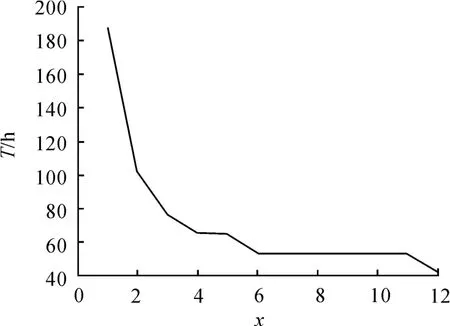
图7 单个工作站吸盘组数x与生产总耗时T的折线图

4.3 运行结果分析

1)当x≤3时，x增加引起工作站数量的减少，导致成本急剧下降，说明工作站的数量导致的加工成本在总成本中占主导地位。工作站铺贴机构采用的是传统的铺贴机构，开发成本相对较低，对总成本的变化影响较弱。

2)当x≥4时，传统的结构和铺贴原理已无法满足功能和精度上的要求，需开发新的铺贴机构，此方面资金投入随着x的增加而剧增，甚至抵偿了工作站数量减少而缩减的成本，使得总成本继续增长。

若能在保证精度和稳定性的前提下，设计出新的成本低廉的铺贴机构，使得单个工作站每次能铺贴更多的马赛克颗粒，并使铺贴机构在总成本中的比重大大减少，那么当x＞4时，总成本将会低于图6中x=3时的最低值，并可能随着x的增加持续降低。

3)随着x的增加和工位数的减少，生产效率不断提高，生产总耗时不断减少。由图7中直线的斜率变化可知:当x＜3时，x每增加1，总耗时的减少都超过20 h，x的增加对生产总耗时的缩减效果非常显著;当x由3增加至11时，总耗时减少约20 h，即意味着当x＞3时，x的增加对缩减生产总耗时的影响明显减弱，此时x的取值更多依据x对生产总成本S的影响。

综合以上分析，在现有技术条件下，x取3既可以得到较低的生产总耗时，也可最低限度地压缩生产成本，可认为是一个较好的平衡点取值。

5 结束语

本文针对多色彩复杂图案玻璃马赛克自动铺贴设备的工作站布局问题提出了一种时间－成本双目标优化模型。在项目开展的初期，总体结构布局的设计对于设备的加工和制造具有重要意义。合理的总体布局能节约成本，缩减设计周期，有效降低迭代返工次数。鉴于工程问题一般具有离散性，优化算法多采用直接法的策略，列出了所有可行解对优化目标的影响。企业可根据实际需要改变输入量的取值，从而选取需要的优化方案。因此本文所提出的模型具有一定的理论和实用价值。

［1］中国马赛克城.中国马赛克行业现状分析［EB/OL］.［2015－04－14］.http://www.mosaiccity.cn/new_view.asp?id=4208.

［2］温胜厚.玻璃马赛克铺贴生产线供料装置的探讨［J］.五邑大学学报:理工版，1988(2):39－43.

［3］黄建，刘亮，齐二石.考虑生产线平衡的多目标混流装配线排程问题研究［J］.组合机床与自动化加工技术，2014(8):156－160.

［4］Oral A，Esra P I.Marble mosaic tiling automation with a four degrees of freedomCartesian robot［J］.Robotics and Computer-Integrated Manufacturing，2009(25):589－96.

［5］Cayiroglu I，Demir B E.Computer assisted glass mosaic tiling automation［J］.Robotics and Computer-Integrated Manufacturing，2012，28(5):583－591.

［6］杜遥雪，陈启瑞.玻璃马赛克自动铺贴生产线的设计与研究［J］.机械设计，1997(6):38－29.

［7］郭安华，陈顺利.马赛克自动铺砖机［P］.中华人民共和国专利，CN200820189506.1，2008.

［8］陈耀灶.马赛克铺贴设备［P］.中华人民共和国专利，201020100940.5，2010.

［9］王永翔，吴志鹏，黎勉.艺术马赛克自动排版生产线设计［J］.机床与液压，2014，42(20):15－18.

［10］于洋，唐加福，宫俊.通过生产线向单元转化而减人的多目标优化模型［J］.东北大学学报:自然科学版，2013，34(1):17－20.

［11］郭红，杨建军.基于改进遗传算法的多行布置车间布局优化［J］.制造业自动化，2015，37(2):24－26.

［12］黄健，刘亮，齐二石.考虑生产线平衡的多目标混流装配线排程问题研究［J］.组合机床与自动化加工技术，2014(8):156－160.

［13］李静，胡军伟.基于蚁群算法的工期－成本问题的优化［J］.北京工业职业技术学院学报，2014，13(1):11－13.

［14］柴月珍.农村固体废弃物回收逆向物流网络优化［J］.重庆理工大学学报:自然科学版，2014，28(9):143－146.

［15］马翠，敖翔，庞剑飞，等.基于优先级的建筑外表面光伏电池铺设优化模型［J］.重庆理工大学学报:自然科学版，2014，28(9):112－116.

［16］傅晨曦，郑永前.基于维护总成本最优的PM周期优化方法和应用［J］.现代制造工程，2014(4):92－97.

［17］赵静，但琦.数学建模与数学实验［M］.北京:高等教育出版社，2008.