基于经济效益循环系统的林区碳汇林投资决策研究

温贝贝

(天津大学管理与经济学部，天津 300072)

近年来，碳交易理念风靡世界，它从市场经济角度为全球实现碳减排提供了一个有效的解决路径［1］。在碳交易体系中，碳汇交易是重要组成部分，它通过市场的手段来实现森林生态价值的有效补偿［2］。碳汇交易的基础在于建立具有碳汇功能的碳汇林，因此碳汇交易制度的设立为林业资源型城市带来一个新的经济增长点——建立碳汇林［3］。这对面临经济、资源、环境等多重困境的林业资源型城市无疑提供了一个实现经济转型的有效途径。

目前，研究学者已经对建立碳汇林的可行性做了大量的理论和实践研究，证实在林业资源型城市建立碳汇林是合理、有效的，并且具有巨大的经济效益［4］。另外，众多学者也研究了碳汇林经济效益的具体计算思路与计算方法:王东至等［5］从光合作用方程式的角度出发，结合生物量法，量化了大青山乔木林的碳汇经济效益数值;程兆伟等［6］将舒兰市森林碳汇的生态效益量化为经济价值，解决了舒兰市森林碳汇效益和生态效益的货币价值量化问题。但是，对碳汇林的投资政策、投资年限和种植规模等问题的研究报道还不多见。本文从林业资源型城市的整体出发，研究政府对碳汇林的投资比例和碳价是如何影响城市整体经济效益的，并通过分析确定出碳汇林的最优投资比例以及政府应在多少年后结束对碳汇林的建林投资。

1 经济效益循环系统

首先，政府对碳汇林进行一定比例的投资，从而形成一定规模的碳汇林。其次，一方面碳汇林可以通过产生碳汇、净化空气、固定土壤、防止水土流失来产生经济效益，增加城市整体经济效益;另一方面由于碳汇林吸收政府投资和占用有林地面积，从而剥夺了其他产业的资源，降低了其他产业的经济效益(比如第一产业用林地的减少会直接减少木材的采伐量，这不仅会减少木材销售收入，还会降低满足居民需求的程度和完成国家开采上缴任务的程度，这些都会在某种程度上影响城市的发展，造成经济效益损失，对于第二、三产业也是如此)，进而减少城市整体的经济效益。最终，以上对整体经济效益的影响会改变经济效益总量，从而又会影响政府对碳汇林的投资。这是一个循环的相互联系又相互制约的系统，如图1所示。

图1 引入碳汇林的经济效益因果循环链

系统动力学的概念和理论最初由Forrester提出［7］，被广泛用于政策的模拟与评价［8］、可持续发展［9］、决策系统［10－11］和系统预测［12］等研究领域中，它能在模拟系统的动态发展变化过程中寻找最优的发展路径［13］，其模型着重于分析系统的循环发展，因此非常适合于分析林业资源型城市的经济效益循环系统。本文采用系统动力学的方法进行建模，将林区的经济效益循环分为4个子系统，即碳汇林投资子系统、碳汇林与其他产业制约子系统、碳汇林经济效益子系统和总经济效益子系统。每个子系统的内部关系如图2所示。由于碳汇林其他效益的经济价值很小，可以忽略，因此在本模型中只考虑碳汇林的碳汇效益、降低环境污染效益、固定土壤效益，并将它们量化为经济数值。本模型只考虑与林业有关的因素，对林业资源型城市来说，其他因素影响较小，本文不做深入探讨。

2 系统动力学建模

2.1 碳汇林投资子系统

碳汇林投资子系统如图2左侧所示。在碳汇林投资子系统中，政府对林业的投资有一部分会流入到碳汇林中，从而引起碳汇林面积的变化。各个变量之间的关系用下式表示:

政府投资=总经济效益×政府投资比例

政府投资比例=初始投资比例×(1+投资比例增长率)(Time－2012)

Time是系统动力学中的时间函数，属于隐藏变量，不需要输入方程。

碳汇林投资=INTEG(碳汇林投资变化量，碳汇林投资初始值)

INTEG(d，e)是系统动力学中表示累计变化的函数，其中:d表示变量的变化量;e表示变量的初始值。上式表示碳汇林投资是历年投资变化量的总和。

碳汇林面积变化量=delay1(碳汇林投资变化量×实际单位投资效率，碳汇林成长时间)

delay1(f，g)是系统动力学中的延迟函数，其中:f表示被延迟的变量;g表示延迟值。上式表示碳汇林在投资种植后，需要一定的生长时间才能实现模型所需要的面积变化。

实际单位投资效率=初始投资效率/(1+通货膨胀率)(Time－2012)

碳汇林面积=INTEG(碳汇林面积变化量，碳汇林面积初始值)

图2 每个子系统的内部关系

2.2 碳汇林与其他产业制约子系统

碳汇林与其他产业制约子系统位于图2的中部。在该子系统中，由于政府对林业的投资和有林地面积的增长是有限的，因此碳汇林对资源的占用必然会引起其他产业所占投资和林业资源面积的减少，进而会造成其他产业经济效益的降低。具体变量之间的关系为:

有林地面积增加量=有林地面积初始量×有林地面积增长率

其他产业面积变化量=碳汇林面积变化量－有林地面积增加量

其他产业面积累计变化量=INTEG(其他产业面积变化量，其他产业面积累计变化量初始值)

其他产业面积减少比例=(其他产业应有面积－(其他产业初始面积－其他产业面积累计变化量))/其他产业应有面积

其他产业应有面积=其他产业初始面积×(1+其他产业面积需求增长率)(Time－2012)

其他产业经济效益损失比=其他产业面积减少比例影响因子表(其他产业面积减少比例)+其他产业投资减少比例影响因子表(碳汇林投资比例)(注:碳汇林的投资比例即其他产业减少的投资比例)

y变量=x因子表(x变量)是系统动力学中的表函数，它用于建立x变量和y变量之间的非线性关系，其中x因子表表示x变量对y变量的影响。表函数中的数值可以由历史数据计算和分析得出，也可以由德尔菲法等方法得到。

其他产业经济效益损失=其他产业经济效益×其他产业经济效益损失比

其他产业经济效益=INTEG(其他产业经济效益增长量，其他产业经济效益初始值)

其他产业经济效益增长量=其他产业经济效益×其他产业经济效益增长率

2.3 碳汇林经济效益子系统

碳汇林经济效益子系统如图2的右上角所示。该子系统反映了建立碳汇林所产生的经济效益(本文所考虑的碳汇林经济效益仅限于碳汇林明显区别于其他产业的部分)，主要包括碳汇价值、降低污染价值以及固土经济效益。各个变量之间的相互关系如下:

碳汇林生物量增加量=碳汇林面积变化量×单位面积生物量

碳汇量增加量=碳汇林生物量增加量×固碳系数

碳汇价值增加量=碳汇量增加量×碳汇价格

可减少环境污染=碳汇林面积变化量×实际吸收率

考虑到实际吸收率会受到季节变化的影响，因此可用以下公式计算实际吸收率:

实际吸收率=较高的吸收效率×选择参数+较低的吸收效率×(1－选择参数)

较高的吸收率是指在树叶比较茂盛时的吸收率，选择参数则表示树叶茂盛时期在一年当中所占比例。

可减少环境投资=可减少环境污染×环境污染治理成本

固土量变化量=碳汇林面积变化量×R×E式中:R表示进入河道或者水库的泥沙占总泥沙流失量的比值;E表示每年有林地比无林地减少的侵蚀量。

可减少疏通投资=固土量变化量×C式中C表示挖去每吨泥沙的成本。

碳汇林经济效益增加量=可减少环境投资+碳汇价值增加量+可减少疏通投资

碳汇林经济效益=INTEG(碳汇林经济效益增加量，碳汇林经济效益初始值)

2.4 总经济效益子系统

总经济子系统位于图2的底部，该系统主要描述了碳汇林产生的经济效益增加量和其他产业的经济效益损失对总经济效益的增减影响，具体如下:

总经济效益变化量=碳汇林经济效益增加量－其他产业经济效益损失

总经济效益=INTEG(总经济效益变化量，总经济效益初始值)

3 模型模拟及结果分析

3.1 参数设定

模型中运用到的大部分数据都是基于某林业资源型城市的真实数据，且来源于该城市历年的统计年鉴。该城市较为适宜种植的林种为针叶林。以2012年为基准年。2012年该城市的有林地面积为3 299 832 hm2，每年的增长率为0.047%。其他产业占用有林地面积为2 999 832 hm2，年需求增长率为0.047%。据统计，成熟针叶林对二氧化硫(二氧化硫为主要空气污染物)的实际吸收率为0.215 6 t/hm2(根据地理位置，模型中选择参数取0.4得到)，每排放1 t二氧化硫造成的经济损失为2万元。该城市总体经济效益的初始值为1 749 183万元，其他产业经济效益的初始值为1 418 580万元，增长率为0.25%。政府对林业的初始投资比例为38.43%，增长率为0.243%。初始的投资效率为0.1 hm2/万元，通货膨胀率选择2002年全国的3.25%。另外，模型中的R取0.5，C取0.0002 万元/t，E取36.85 t/hm2。

由于碳汇林是新项目，风险和收益都有很大的不确定性，因此初始建林规模不宜过大，设为300 000 hm2。森林的固碳量采用生物量法计算，根据光合作用方程式，固碳系数为1.63。碳价选取2012年Bluenext交易所EUA现货平均价格，折算成以人民币计量为51.16元/t。

模型中重要的表函数，即其他产业面积减少比例影响因子表是在综合考虑该城市整体情况下，将其他产业分为第一、第二、第三产业分别分析并乘以相应的产业比例得到，其值为:［(0，0)—(1，20)］(0，0)，(0.05，0.05)，(0.1，0.11)，(0.15，0.18)，(0.2，0.3)，(0.3，0.6)，(0.4，2)，(0.5，3)，(1，20)，其中:［ ］中的()内的值分别是自变量和因变量的最小值和最大值;后面的9个()内的值则分别是自变量和因变量的其他对应点。若自变量的值不在给定点中，则模型自动用线性插值法求出因变量的值。

模型中另外一个表函数即其他产业投资减少比例影响因子表的取值方法与其他产业面积减少比例影响因子表相同，其值为:［(0，0)—(1，6)］(0，0)，(0.05，0.03)，(0.1，0.06)，(0.15，0.12)，(0.2，0.18)，(0.3，0.4)，(0.4，0.8)，(0.5，1.5)，(1，6)。

此外，本文的研究模型是在其他的国家和政府政策基本维持不变的情况下模拟的，并且通过了真实性检验。

3.2 结果分析

1)当前情况下模拟结果

结合图3分析，在当前政策条件下，即政府的碳汇林投资比例为10%，碳价维持在51.16元/t时，总经济效益先快速增长，并在2044年达到最大值，随后迅速减少，这说明在2044年总经济效益已经达到最优，故政府不需要再继续追加建立碳汇林的投资，只需进行正常维护即可。此时的碳汇林面积为582 289 hm2，即为碳汇林的最优面积。

图3 当前政策条件下模拟结果

2)碳汇林投资政策的灵敏度分析及最优投资比例确定

在碳价维持在51.16元/t不变的前提下，本文对比分析了在5种不同投资比例情况下的总经济效益走势情况，即碳汇林投资分别设为10%，12%，15%，18%以及 20%。如图4所示，当投资比例不同时，总经济效益的增长速度和最优值均不相同。但它们的相同点是当碳汇林投资比例给定时，我们就能确定出政府应该在哪一年停止对碳汇林的种植追加投资。

由图4还可以看出，碳汇林的投资比例为15%时的经济效益最优值要明显高于其他情况下的经济效益最优值。因此，15%的投资比例即为最优的投资比例，此时的经济效益最优值为5 758 650元，在2044年达到。

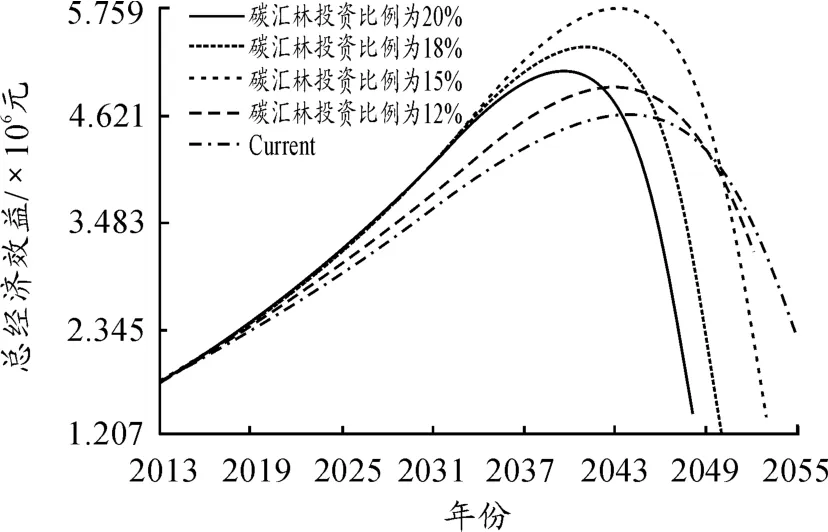
图4 碳汇林投资政策的灵敏度分析

3)市场上碳价的灵敏度分析

在碳汇林投资比例维持在10%的前提下，本文对比分析了在3种不同的碳价情况下的总经济效益走势情况，即碳汇价格分别上下浮动10%。如图5所示，当碳价波动时，总经济效益的增长速度和最优值均不相同，且碳价越高，总经济效益达到最优值的时间越晚。但其共同点都是当碳价给定时，就能确定出政府应该在哪一年停止对碳汇林的种植追加投资。

此外还可以看出，总经济效益对碳汇价格的敏感性较强，因此投资碳汇林有很大的价格风险，是一个高收益、高风险的项目，需要谨慎对待。

4)碳价决定是否投资碳汇林

显然，当市场上的碳价为0时，即碳市场失效时，政府没有必要投资碳汇林。因此我们需要模拟出有必要进行碳汇林投资的最低碳价。在模型中，对碳价分别取24，25和26元/t，结果见图6。可以看出，当价格为24元时，整体经济效益一直处于递减状态，而当碳价为25元/t和26元/t时，整体经济效益出现了递增的情况，即说明当碳价等于或者大于25元/t时政府才有必要去投资碳汇林。模型中所求的25元/t是在建立碳汇林会对其他产业产生冲击的前提下的最低投资价格，如果建立碳汇林对其他产业没有冲击或者冲击较小，则无论碳市场是否有效，即无论碳价是多少，建立碳汇林总是有效益的。

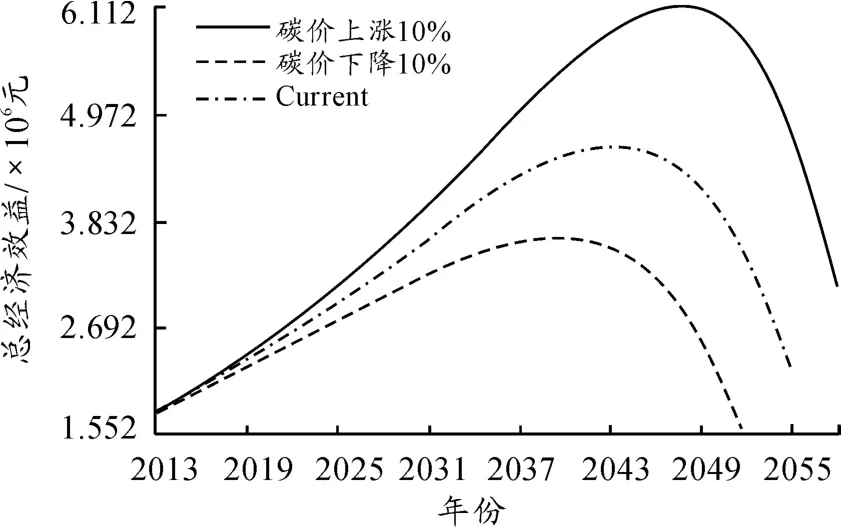
图5 碳汇价格灵敏度分析结果

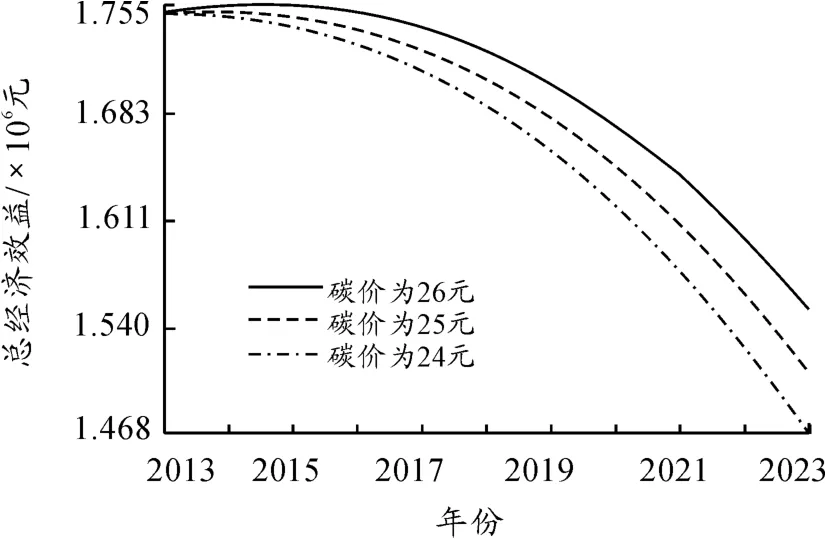
图6 碳汇价格决定是否投资图

4 结论

1)当政府对碳汇林的投资比例逐渐增大时，总经济效益曲线表现出波峰逐渐提高、达峰时间逐渐提前的波动规律。这说明，一方面政府不能盲目地增加碳汇林的投资比例，另一方面需要在碳汇林的投资比例和投资年限之间做出有效权衡:若投资年限较短，则可选择15%左右的投资比例;若投资年限较长，则适宜选择较低的投资比例;

2)当市场上碳价逐渐增大时，总经济效益曲线表现出波峰逐渐提高、达峰时间逐渐延后的波动规律。在同一时间，碳价较高的经济效益总是优于碳价较低的经济效益。但是经济效益对碳价波动的敏感性很强，碳汇林的投资存在很大的价格风险。

3)政府在投资碳汇林时需要充分考虑上述因素，在此基础上，可以通过对市场上碳价的预测来合理地确定投资比例，并预测出停止追加碳汇林建立投资的大致时间范围。如果在投资期内碳价出现波动，政府应当据此规律及时做出调整，以规避风险，强化收益。

［1］骆华，费方域.国际碳金融市场的发展特征及其对我国的启示［J］.中国科技论坛，2010(12):142－147.

［2］谢高地，李士美，肖玉，等.碳汇价值的形成和评价［J］.自然资源学报，2011(1):1－10.

［3］余光英.基于交易视角的碳汇林管理的有效机制研究［J］.生态经济，2010(7):52－54.

［4］杨华.国有林区发展碳汇经济大有可为——对黑龙江省伊春市的调查分析［J］.中国金融，2009(16):44－45.

［5］王冬至，张秋良，张冬燕.大青山乔木林碳汇效益计量［J］.山东农业大学学报:自然科学版，2010(4):522－526.

［6］程兆伟，岳晓辉，秦增亮，等.舒兰市森林碳汇与其他生态效益分析［J］.中国林业经济，2010(1):45－47.

［7］Forrester J W.Industrial Dynamics［M］.MIT Press:Cambridge，MA，1961.

［8］Saleh M，Oliva R，Kampmann C E，et al.A comprehensive analytical approach for policy analysis of system dynamics model［J］.European Journal of System and Software，2001，203(3):673－683.

［9］Shen Q P，Chen Q，Tang B S，et al.A system dynamics model for the sustainable land use planning and development［J］.Habitat International，2009，33(1):15－25.

［10］Yim N H，Kim S H，Kim H W，et al.Knowledge based decision making on higher level strategic concerns:System dynamics approach［J］.Expert System with Applications，2004，27(1):143－158.

［11］王建军，李莉，谭忠富，等.电力需求侧响应利益联动机制的系统动力学模拟［J］.系统工程理论与实践，2011(12):2287－2295.

［12］Erma S，Chou S Y，Chen C H.Air passenger demand forecasting and passenger terminal capacity expansion:A system dynamics framework［J］.Expert System with Applications，2010，37(3):2324－2339.

［13］张力菠，韩玉启，陈杰，等.供应链管理的系统动力学研究综述［J］.系统工程，2005(6):8－15.