运用遗传算法的磁流变阻尼器减震的模糊控制
林秀芳,陈淑梅,陈金兰
(1.福建农林大学金山学院,福州 350002;2.福州大学机械工程及自动化学院,福州 350108)
近年来,磁流变阻尼器已经成为减振领域中一种非常重要的半主动控制装置[1-5]。然而它具有很强的非线性特性,阻尼力不能直接控制,只有电压可以直接控制,因而在控制过程中往往要求从期望阻尼力反算出控制电压。虽然Spencer等[6]通过磁流变阻尼器的现象模型可以比较精确地预测阻尼力,但难以计算磁流变阻尼器所需的用于获得理想控制力的输入电压值。
目前,模糊逻辑、神经网络、进化计算等人工智能的研究成果已经在结构振动控制领域得到应用。其中,由于模糊逻辑控制具有搭建非线性控制规则架构的能力,且该规则对不确定和不精确的数学模型具有很强的适应性(即无需依赖数学模型,且具有较强的鲁棒性),因此成为解决上述控制问题的一种重要方法。近些年,模糊逻辑控制在结构振动控制领域中的应用研究备受科研人员和工程师的关注[5,7],如 Choi等[7]首次成功地将模糊控制用于磁流变阻尼器的结构减震中。
模糊逻辑控制系统的设计过程往往依赖于人工经验和领域专家的先验知识,例如隶属函数的参数和模糊规则必须预先给定,且需要不断调整,因此限制了其优点的充分发挥。为弥补模糊逻辑控制系统在结构-磁流变阻尼器减振控制中的不足,将模糊控制器和智能算法结合起来成为设计模糊逻辑控制系统的热点。目前用遗传算法优化模糊控制器从而实现阻尼器对建筑结构的减震控制已成为热点[8-12]。文献[8-11]用遗传算法优化的模糊控制器实现磁流变阻尼器对结构的仿真控制,文献[12]对文献[8]的理论研究进行了实验验证。然而这些研究都仅限于用遗传算法优化模糊控制器的模糊规则,而模糊控制器的其他参数是预先给定的,因此限制了其优势的充分发挥。另外,二进制的编码形式也使遗传算法只能进行交叉和选择的变异操作[8-9]。
本文提出一种具有混合编码方式的基于遗传算法的磁流变阻尼器模糊控制方法。为充分发挥模糊控制方法的特性,对其主要的参数进行优化,包括隶属函数的参数和模糊规则。为了证明该算法的有效性,本文将该算法与零电压控制方法和只优化模糊规则的模糊控制方法进行了比较。
1 模糊控制器的优化设计
在传统设计方法中,模糊控制器的参数(如隶属函数和控制规则)通常是根据试误法确定的。这种方法对人工经验及领域专家先验知识的依赖性很强,且工作效率低,因而亟待对模糊控制器的参数进行优化。本文以在第1层装有磁流变阻尼器的一个3层建筑结构为例,对模糊控制器的优化设计进行探讨。
1.1 输入输出的模糊化
在进行模糊控制器的设计时,首先要选择适当的输入量和输出量。考虑到加速度是实际应用中最易(用传感器)采集到的结构响应,因此本研究以结构的最高两层的加速度响应作为所设计的模糊控制器的输入。输入磁流变阻尼器的控制电压作为模糊控制器的输出。将每个输入(加速度)和输出(电压)的隶属函数值都分成5个区域,输入的语言变量均为NL,NS,Z,PS和PL,输出的语言变量为VS,S,M,L 和 VL。
1.2 优化参数和编码
因为在相同输入值的情况下,隶属函数的类型和分布不同,故输出值很可能也不同。由于钟形隶属函数通过调整自身参数可以逼近其他隶属函数,因此本研究采用钟形隶属函数:
其中:a,b和c为隶属函数的半宽、斜度和中心。对每个隶属函数的a和b参数进行优化。隶属函数的总数为15个,故待优化的隶属函数的参数总数为30个,均采用实值(浮点数)的编码形式。
模糊规则采用“if-then”的形式进行表达,例如规则i:如果输入1是NL且输入2是PL,则输出为M。
由于输入数目为2,每个输入有5种可能性,故该规则表由25个规则组成,且均采用非实值的编码形式。即在编码中用1~5的整数分别代表VS,S,M,L和VL。遗传算法的混合编码结构如表1所示。
2 优化的目标函数
研究时需要兼顾建筑物的安全性和其中人员的舒适性,其中:位移是与安全性有关的参数;加速度是与舒适性有关的参数。因此,遗传算法优化的目标函数定义为

式中:

其中:xi(t)和ai(t)分别是第i层楼的相对位移和绝对加速度;xun和aun分别是建筑物在不受控时的最大位移和最大绝对加速度;J1和 J2分别是最大位移和最大加速度响应最小化的单目标函数;α是反映J1和J2相对重要性的权重。
3 仿真实验
3.1 仿真条件
采用一个3层建筑物结构作为受控对象,其使用磁流变阻尼器减震的建筑结构如图1所示。
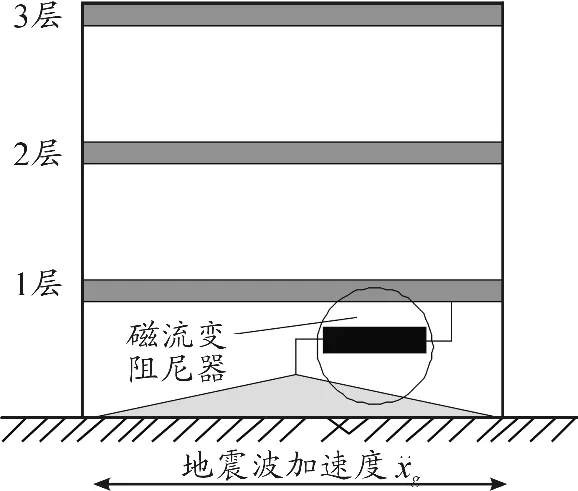
图1 使用磁流变阻尼器减震的3层建筑结构
在第1层和地面之间安装1个磁流变阻尼器。该结构的各层质量均为98.3 kg,1~3层的刚度分别为619 200,820 800和820 800 N/m。其质量(kg)、阻尼(Ns/m)和刚度(N/m)矩阵分别为[13]:

对该结构采用El-Centro地震波进行激励,采样频率为0.02 s,激励时间为20 s。由于建筑物是一个缩尺的模型,按照结构相似度原则,把地震加速度加速5倍作为该模型的激励。遗传算法的具体参数为:种群规模为220,变异概率和交叉概率分别为0.1和0.9,迭代次数为100。进化操作选用转盘选择和双点交叉方法。令式(2)中的权重α=0.5。以第2层和第3层的加速度响应作为模糊控制器的输入,输出为磁流变阻尼器的控制电压。仿真中用到的磁流变阻尼器的力学模型采用目前广泛使用的文献[6]提出的现象模型。模糊控制的电压值的上限为2.25 V。
3.2 仿真结果和对比
图2是基于遗传算法模糊控制的目标函数值的收敛曲线。曲线1为仅优化模糊控制器的模糊规则的迭代结果,曲线2为同时优化隶属函数和模糊规则的迭代结果。为了方便比较,曲线1所采用的遗传算法的具体参数与曲线2的参数完全相同,包括种群规模、迭代次数、变异概率、交叉概率、进化操作方法以及目标函数。由图2可知:同时优化隶属函数和模糊规则的方法能获得更小的目标函数值。由于仅优化模糊规则这种方法的优化参数的数量较少,使得初始种群相对不够理想,因此其在100代时的目标函数值接近于本文方法的初始目标函数值。值得注意的是,对于本文算法,如果采用更大的迭代次数以及种群数,目标函数值还将减小,控制效果也将更好。

图2 遗传算法优化模糊控制器参数的迭代曲线
表2比较了地震波激励下的无控和各种控制方法作用下的响应波峰值。表2中:xi,di和¨xi分别是第i个楼层的相对位移、层间位移以及绝对加速度的峰值;F是控制方法中所需的磁流变阻尼器的最大阻尼力。表2中的百分数是各种控制方法作用下的响峰值相对于无控制时的响应峰值的减小率。模糊控制1是与图1中的曲线1相对应的只优化模糊规则的方法,模糊控制2是本文提出的控制方法,即基于混合编码遗传算法的同时优化模糊规则和隶属函数的模糊控制方法。当只优化模糊控制器的模糊规则时,最大(第3层)位移相对于无控时的位移减小了70%,最大(第3层)加速度相对于无控时的加速度减小了62%。当采用本文方法时,最大位移和最大加速度的减小率分别为74%和67%。这两项峰值指标是作为遗传算法优化的目标,而图2结果表明单纯优化模糊规则的控制方法产生的目标函数值大于本文方法的目标值。
由表2可知:尽管算法优化的对象是所有楼层中的最大位移和最大加速度(见式(2)),但本文提出的基于混合编码遗传算法的模糊控制方法可以明显地减小各楼层的位移、层间位移和加速度响应峰值。虽然为磁流变阻尼器提供0 V电压的控制方法也能产生减震效果,但相比本文方法,只有第1层的加速度峰值和最大阻尼力稍小,其他几项峰值都不如本文方法的结果好。相比只优化模糊规则的模糊控制方法的结果,本文方法的结果全部都比其他好。因此,通过这几种方法的比较,表明本文所提出的算法的综合减震效果最好。

表2 地震波激励下的响应峰值的比较
表3和图3是采用本文方法优化后的模糊控制器的模糊规则和模糊规则曲面。图4为采用本文方法优化后的模糊控制器的隶属函数。

表3 优化后的模糊控制器的模糊规则

图3 优化后的模糊控制器的模糊规则曲面

图4 优化后的模糊控制器的隶属函数
为了更直观地显示本文方法的减震效果,图5和图6分别比较了不受控制条件下和利用本文提出的基于混合编码遗传算法的模糊控制条件下的所有楼层的位移时程响应和加速度时程响应,其中:虚线代表不受控的响应;实线代表受控的响应。

图5 受控和不受控情况下的位移响应的比较

图6 受控和不受控情况下的绝对加速度响应的比较
优化后的电压和阻尼力的时程图分别如图7、8所示。由这两图可知:阻尼力的变化趋势和电压的变化趋势是基本一致的,说明当对磁流变阻尼器施加电压时,阻尼力可以间接地得到控制。虽然模糊控制中设定的电压上限值为2.25 V,但实际优化后的模糊控制器产生的电压值最大不超过1.3 V。
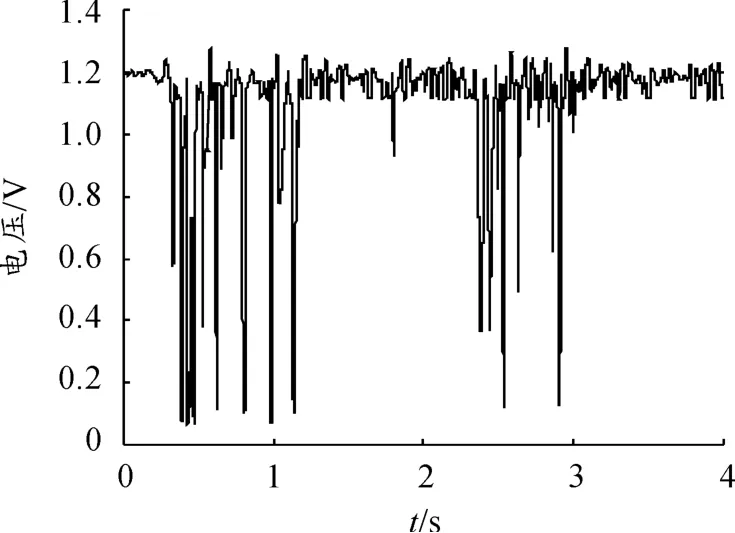
图7 优化后的电压-时程图
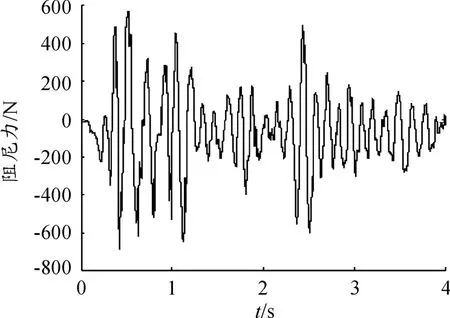
图8 优化后的阻尼力-时程图
4 结束语
为充分发挥磁流变阻尼器的减震性能,开发了将混合编码的遗传算法和模糊控制相结合的半主动控制方法。首先用多目标遗传算法优化模糊控制器的主要参数,包括隶属函数参数和模糊规则。为同时优化这些参数,提出实值编码和非实值编码相混合的遗传算法编码形式。然后利用优化后的模糊控制器为磁流变阻尼器提供产生阻尼力的最优电压值。以磁流变阻尼器-结构减震系统为例进行仿真,结果表明:本文提出的利用混合编码的遗传算法优化获得的模糊控制器明显地减小了结构的地震响应。今后的研究将着力于改进遗传算法以提高优化的效率和改善优化的效果。相应的实验验证也将是今后的研究内容。
[1]刘石,仲继泽,冯永新,等.使用磁流变阻尼器的大型汽轮发电机定子端部绕组振动控制[J].西安交通大学学报,2013,47(4):39-43.
[2]崔治,葛友华,田晓峰,等.磨削压力控制用磁流变液阻尼器设计[J].机械设计与研究,2012,28(6):60-66.
[3]赵强,米磊,尹佳星.基于磁流变阻尼器的车辆悬架振动优化控制[J].武汉理工大学学报:交通科学与工程版,2013,37(2):241-245.
[4]朱永凯,时光志,夏华波,等.磁流变阻尼器在船舶减振中的应用[J].舰船科学技术,2014,36(1):79-83.
[5]胡财宝,丁建国.基于模糊控制的 MR阻尼器在结构抗震中的应用研究[J].世界地震工程,2014,30(4):269-274.
[6]Spencer B F,Dyke S J,Sain M K,et al.Phenomenological model for magnetorheological dampers[J].Journal of Engineering Mechanics,1997,123(3):230-238.
[7]Choi K M,Cho S W,Jung H J,et al.Semi-active fuzzy control for seismic response reduction using magnetorheological dampers[J].Earthquake Engineering and Structural Dynamics,2004,33(6):723-736.
[8]Yan G,Zhou L L.Integrated fuzzy logic and genetic algorithms for multi-objective control of structures using MR dampers[J].Journal of sound and vibration,2006,296(1):368-382.
[9]汪权.建筑结构地震响应半主动控制的遗传-模糊算法[J].地震工程与工程振动,2010(6):127-133.
[10]Kazemi,Bidokhti K,Moharrami H,et al.Semi-active fuzzy control for seismic response reduction of building frames using SHD dampers[J].Structural Control and Health Monitoring,2012,19(3):417-435.
[11]孙欣,丁建国,朱炜.基于优化模糊控制规则的磁流变阻尼减震结构地震反应分析[J].工程抗震与加固改造,2015,37(1):51-63.
[12]胡家亮,周丽,严刚.基于磁流变阻尼器的结构模糊半主动控制实验研究[J].振动与冲击,2009,28(3):131-135.
[13]Dyke S J,Spencer Jr B F,Sain M K,et al.Modeling and control of magnetorheological dampers for seismic response reduction[J].Smart Materials and Structures,1996,5(5):565.

