一种基于自适应变结构的高超滑翔飞行器控制方法研究

常莹莹 王小虎 何 纯 刘雄飞

北京控制与电子技术研究所，北京100038

高超声速滑翔飞行器是指飞行马赫数大于5， 在大气层内和跨大气层中飞行的无人飞行器，目前已成为国内外许多学者关注的焦点。高超声速滑翔飞行器在再入过程中气动特性变化剧烈、非线性以及通道间的耦合非常严重，所以需要一种鲁棒性强，控制精度高的姿态控制算法。

目前对于这种非线性系统控制器的设计，工程上一般采用传统的变增益协调控制方法，这种方法在X －43A 飞行过程中得到了成功应用。但X －43A 的整个飞行过程为巡航下的直线飞行，飞行包线变化范围小，飞行时间短，当飞行包线范围扩大、外界扰动增强时，变增益协调控制方法需要有极大量的增益预置表，且切换过程中参数往往产生突变，严重影响系统的控制性能。最近十几年来，人们不断努力研究各种非线性控制算法来提高高超声速滑翔飞行器的性能［1－3］。对于存在模型不确定性和非线性强耦合的系统，滑模控制是一种有效的鲁棒控制方法［4－6］，其特点为一旦系统进入滑模面，系统状态的转移就不再受系统参数与外界扰动的影响。因此，滑模控制系统的鲁棒性和不变性成为它得到普遍重视和应用的一个重要原因。

本文结合了文献［7 －8］的非线性变结构控制思想和在线估计技术，设计了高超声速滑翔飞行器的变结构自适应姿态控制器。将结构干扰力矩、非线性耦合、气动参数摄动等不确定因素视为一类有界干扰，并根据Lyapunov 稳定方法设计了外部干扰界值的自适应律，从而对系统中的不确定因素进行补偿。选择适当的趋近律提高控制系统动态品质，证明了在改进趋近律后该控制方法的滑动模态是Lyapunov 渐近可达的。通过符号函数连续化方法解决由于变结构控制带来的抖振问题，最后通过对某型滑翔飞行器的数学仿真验证了方法的有效性。

1 高超声速滑翔飞行器数学模型的建立

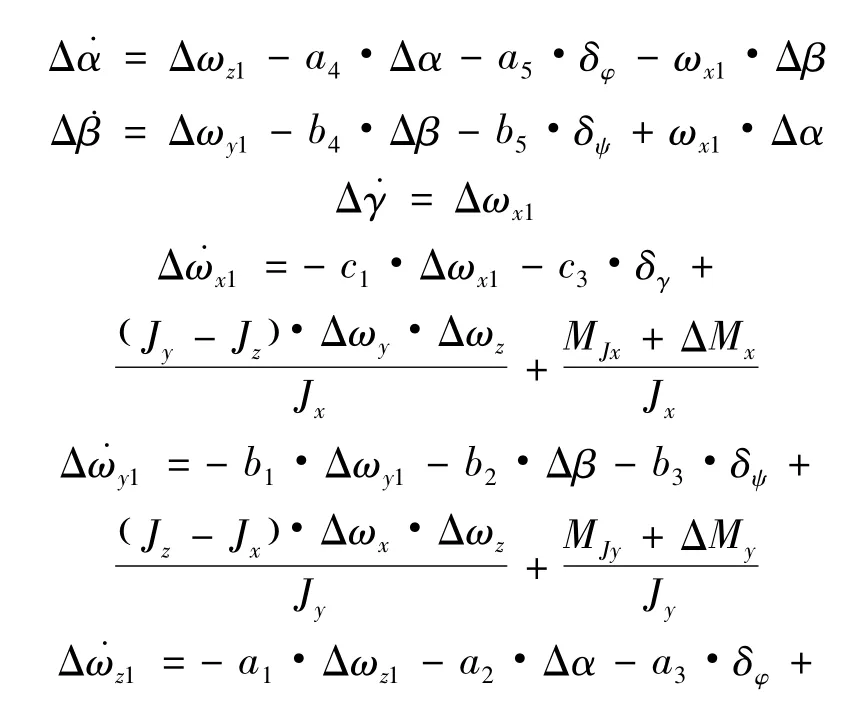
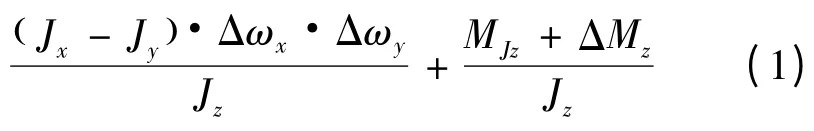
式中，α，β，γ 分别为攻角、侧滑角和滚转角;ωx1，ωy1，ωz1为飞行器绕弹体坐标系的转动角速率;δφ，δψ，δγ分别为飞行器的俯仰、偏航和滚转通道舵偏角;Jx，Jy，Jz为飞行器绕弹体轴的转动惯量;MJx，MJy，MJz为结构干扰力矩;ΔMx，ΔMy，ΔMz为气动参数的不确定性产生的干扰力矩;a1～a5，b1～b5，c1，c3为时变的气动参数。由式(1)可见，ωx1·Δβ和ωx1·Δα 为运动学耦合项，为惯性耦合项，高超声速滑翔飞行器一般设计为面对称升力体外型，故其沿各弹体轴的转动惯量不同。此外，其滚转速率很大，有时甚至达到几百度每秒，造成了3 通道之间运动的严重耦合。

整理模型(1)可建立高超声速滑翔飞行器数学模型非线性状态方程的标准形式为:

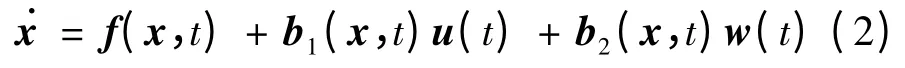
引入状态变量x = ［Δα Δβ Δγ Δωx1Δωy1Δωz1］T，不考虑执行机构的动态特性时近似认为δφc=δφ，δψc=δψ，δγc=δγ，即认为u =［3δφδψδγ］T，表示期望的舵摆角指令，w = ［MJx+ ΔMxMJy+ ΔMyMJz+ΔMz］T表示结构干扰力矩和气动参数的不确定性产生的干扰力矩，在这里视为干扰量。

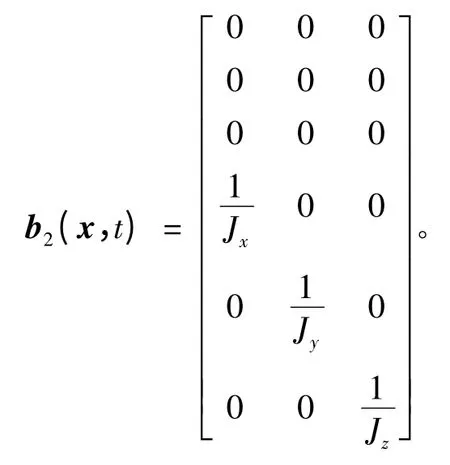
2 高超声速滑翔飞行器自适应变结构控制器设计

假设1:外部扰动输入w(t)是有界的，且满足0 ≤‖w(t)‖≤a，a 是正常数。

本文考虑的控制问题是使式(2)定义的闭环系统稳定，即设计一个有界控制u( )t ，0 ≤‖u( )t ‖≤umax，umax是正常数，使得系统的状态x( )t 从某一初始状态出发在有限时间内转移到平衡状态。即:

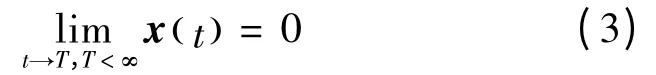
控制器设计需要满足2个条件:

1)系统的状态在有限时间t1内达到切换平面上;

2)系统状态在t1≤t ≤∞内，保持在切换平面内滑动。

对式(2)定义的系统，选取如下切换平面

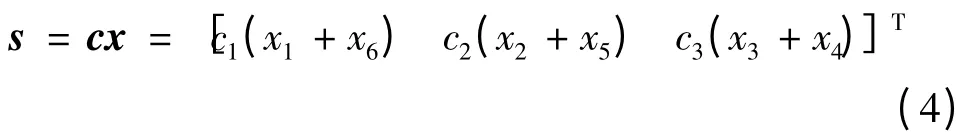
不考虑系统中的不确定性，则非线性系统变为:

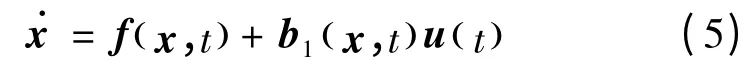
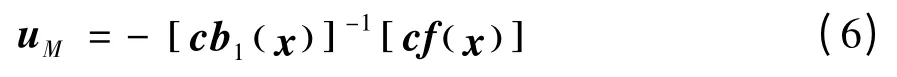
uM为将系统的状态保持在切换平面内所需要的控制量，称为等价控制，而系统中的不确定性可以通过如下不连续控制加以抑制补偿，

即:

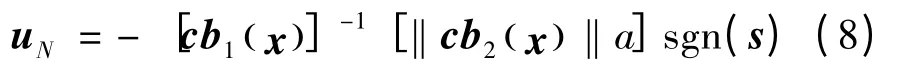
uN用于克服不确定干扰的影响，并使系统状态满足滑动模态的可达条件所需的控制量。

u 为对系统施加的总的控制［7］。

定理1 对于变结构控制律u = uM+ uN，可使不确定非线性系统式(2)在满足假设1 的条件下，在有限的时间内达到并保持在切换平面s 上。

证明:

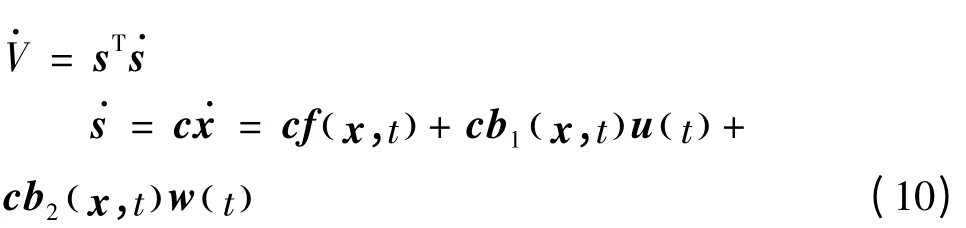
将式(9)的控制律代入系统式(2)中，并结合式(10)，可得:

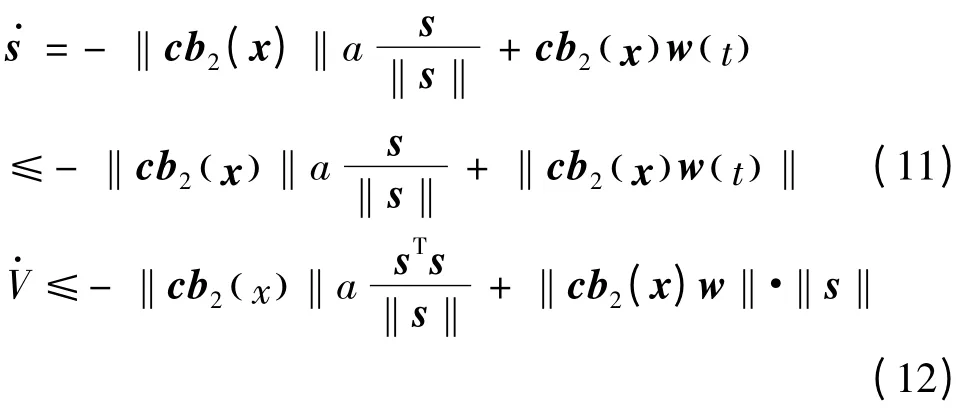
整理得:

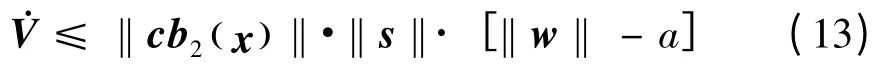
假设‖cb2( )x ‖·‖s‖ = μ ＞0 ，‖w‖ －a ≤－ b，因此＜－ μb，a，b，μ 均为正常数，系统的滑动模态是可达的，滑动模态的可达性条件能满足。

为了获得更强的鲁棒性能，取指数趋近律˙s =－ Ks － εsgn(s)，不考虑系统中的不确定性时，得:

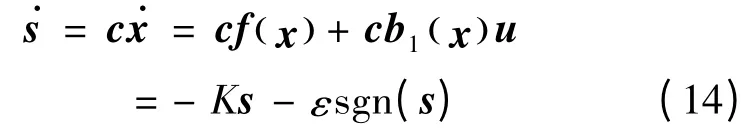
则等效控制变为:

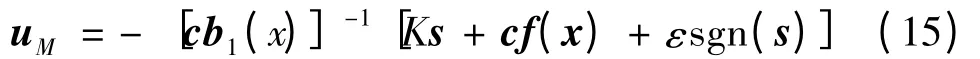
其中，K ∈R3×3，是非负定的。K 主要影响切换函数的动态过渡过程，一般取K 比较大，K 越大系统达到滑模面的速度越快;系统的抖振与ε 成正比，一般取ε 比较小，以防止抖振。

定理1 证明了不考虑趋近律时，滑动模态满足可达条件，下面证明考虑指数趋近律时系统滑动模态的渐近可达性。

定理2 变结构控制律式(7)、(9)和(15)对于多变量不确定非线性系统式(2)，在假设1 成立的前提下系统滑动模态是渐近可达的。

证明:

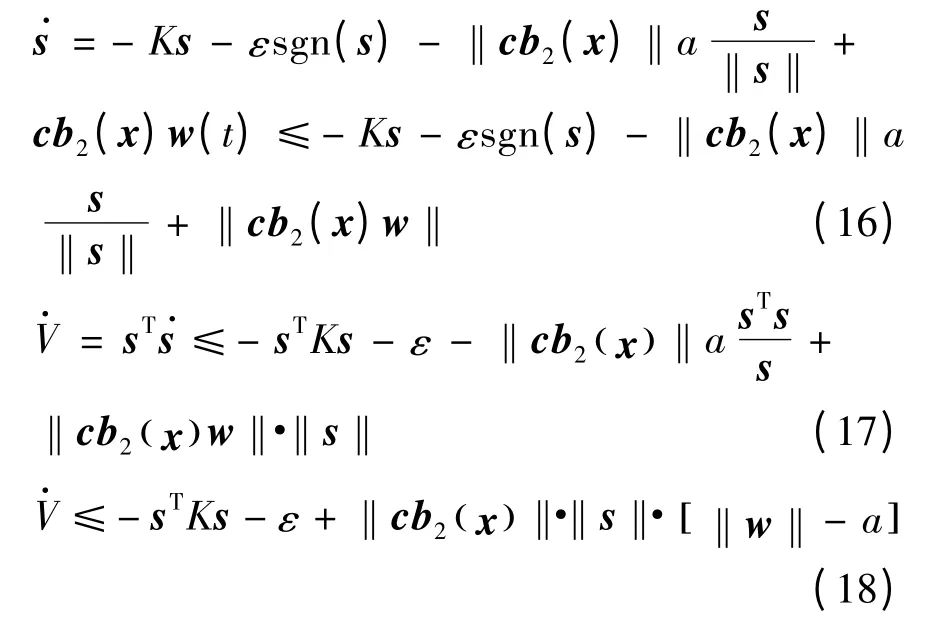
假设‖cb2(x)‖·‖s‖ = μ ＞0 ，‖w‖ － a≤－ b，因此＜－ sTKs － ε － μb，a，b，μ 为正常数，系统的滑动模态是可达的，滑动模态的可达性条件能满足。

由上面推导出的控制律式(8)可知:无需精确知道结构干扰和气动参数摄动的值，但需知道其界值a。实际上界值的选取可根据经验人为确定为某一常数，然而对于保守的取值需要使用过量的控制，反过来过低的估计将会造成系统的不稳定。也就是说如果a 选取过大，则会使控制过量;若a 选取过小，则会使系统不稳定。因此，需要设计一种自适应估计器，使得跟踪a，即使当t →∞时，e = a－取得最小值，其中为a 的估计值，e 为a 估计的误差值。

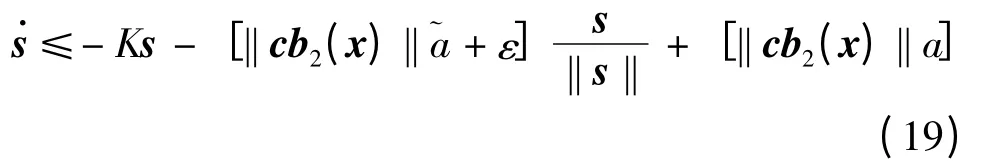
则

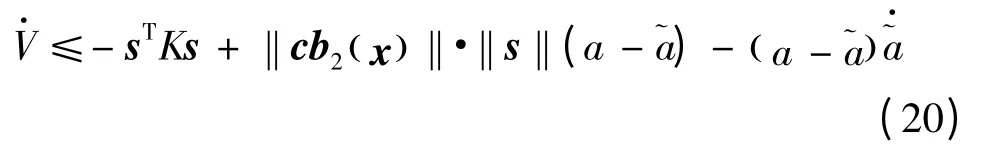
由式(8)和(15)可知，控制器中含有符号函数sgn(s)，符号函数会产生高频抖振，工程上无法实现，有文献仿真证明使用饱和函数sat(s)代替符号函数抖振现象也不会消失［9］。本文借鉴自抗扰控制技术［10］中的幂次函数fal(s，α，δ)代替符号函数，幂次函数是一种非线性函数，利用它可以产生许多智能性功能，文献［11］已给出了幂次函数无抖振的理论证明，其表达式为:

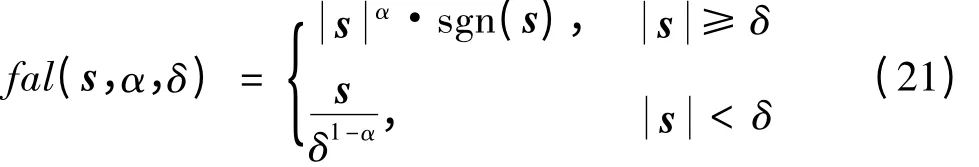
式中，0 ＜α ＜1 ，0 ＜δ ＜1 。

3 数学仿真结果及分析

以某型滑翔飞行器为例进行仿真验证，分别使用本文方法和传统的“前馈+PD”控制方法进行仿真验证，仿真分2 部分:1)特征点仿真;2)弹道仿真。

1)特征点仿真

根据BTT 飞行器的协调要求，直接令侧滑角指令为0，取固定的攻角指令(αc=10° )，考察固定攻角指令下大滚转角指令(γc= 80° )对侧滑角的影响，图1 和2 为不考虑结构干扰和外部干扰的影响时侧滑角与滚转角的过渡过程曲线。

为考察结构干扰和外部其它扰动时本文设计的控制器性能，取结构干扰和外部其它扰动为有界的正弦信号，图3 和4 为用本文方法与传统方法的侧滑角与滚转角的过渡曲线。从图中可以看出，当无外界干扰时传统方法和本文方法均能使系统稳定，但传统方法的过渡过程差，当加入外界干扰时传统设计方法鲁棒性很差，如不调整参数，系统可能会不稳定，而本文设计的控制器具有很强的鲁棒性，在干扰大范围变化的情况下，控制系统仍具有良好的动态品质和较高的跟踪精度。

2)弹道仿真

在考虑各种典型极限干扰(结构干扰、气动系数偏差、大气密度偏差和风干扰等)条件下用本文方法与传统方法进行仿真对比，控制效果的对比曲线如图5 ～10 所示。从仿真曲线可以看出，在线估计器能很好的估计外界干扰，从而能更准确地对其进行补偿抑制，3 通道均能快速、准确地跟踪指令信号，过渡过程平滑，角偏差小。

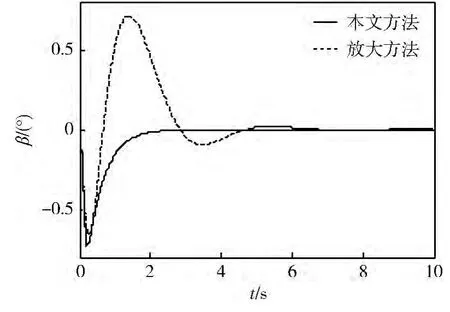
图1 侧滑角(无干扰)

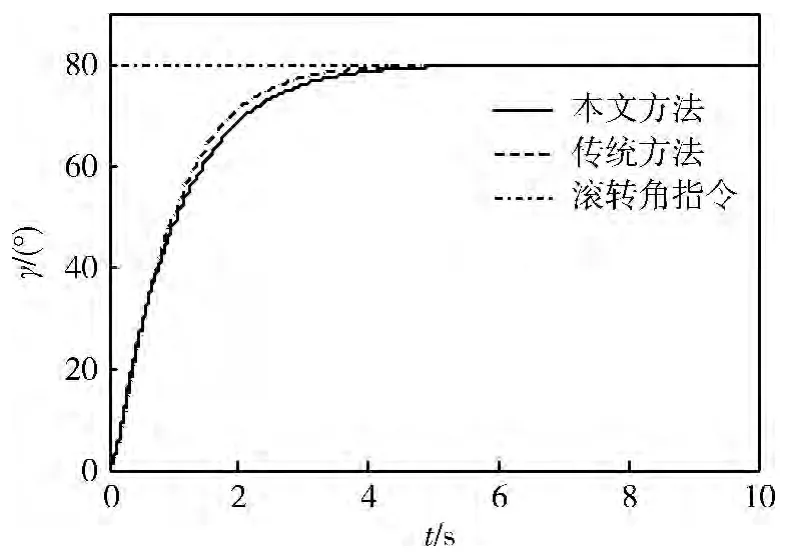
图2 滚转角(无干扰)

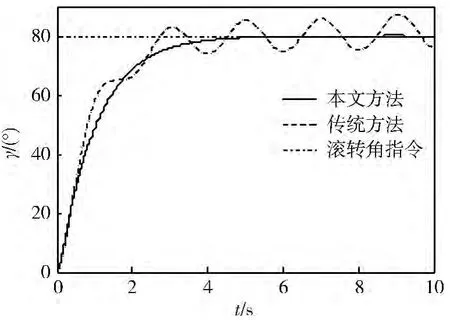
图3 侧滑角(有干扰)

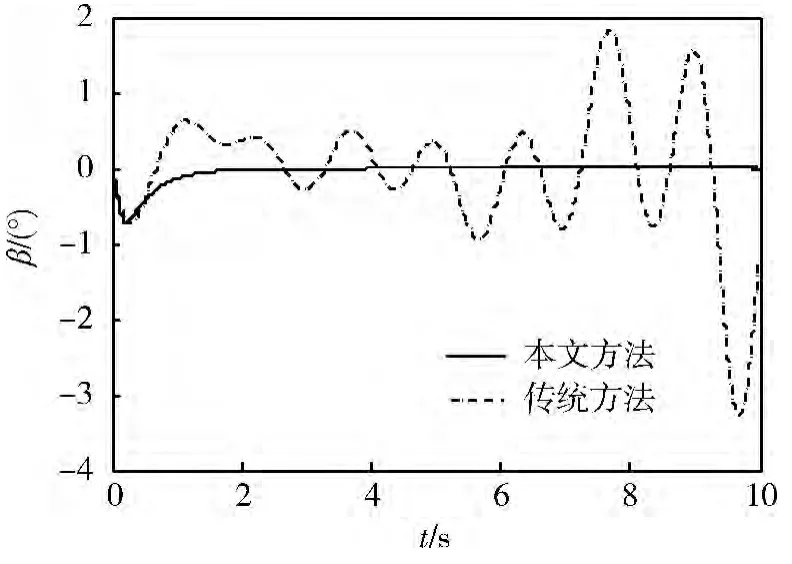
图4 滚转角(有干扰)

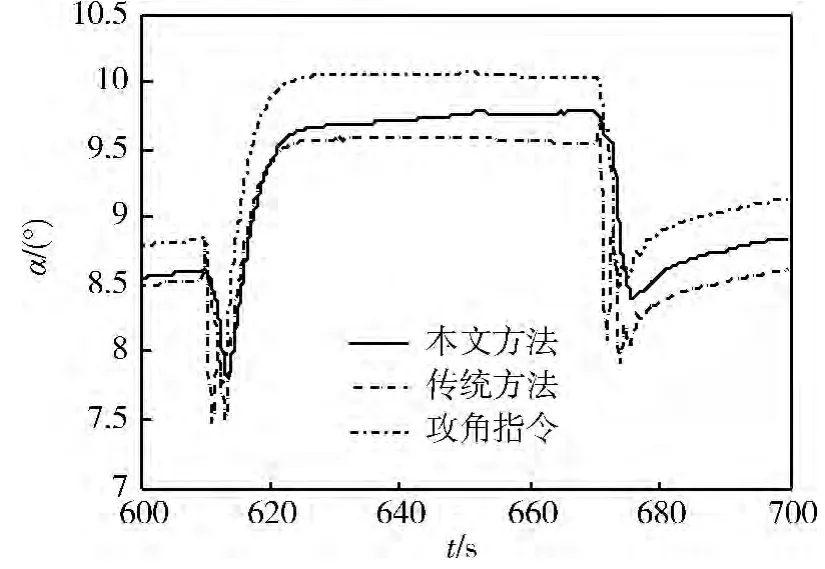
图5 攻角

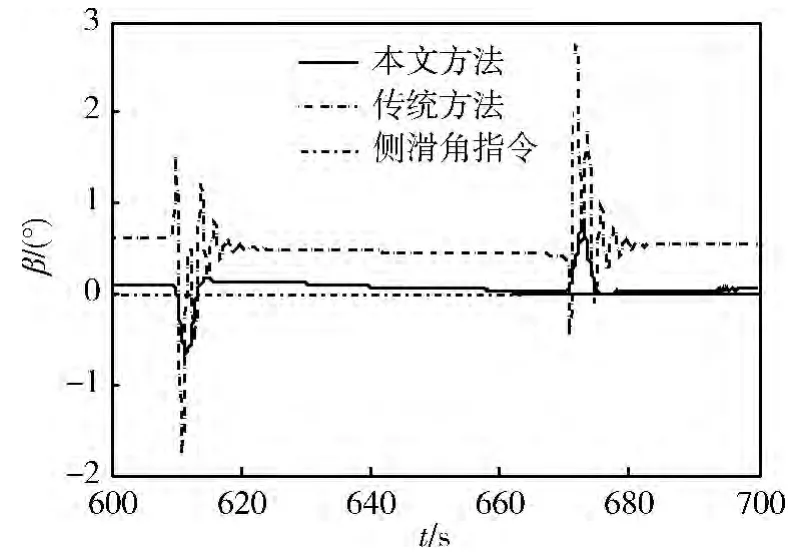
图6 侧滑角

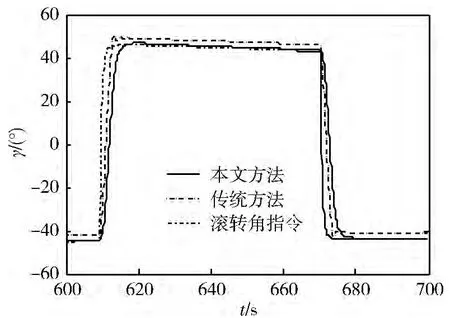
图7 滚转角

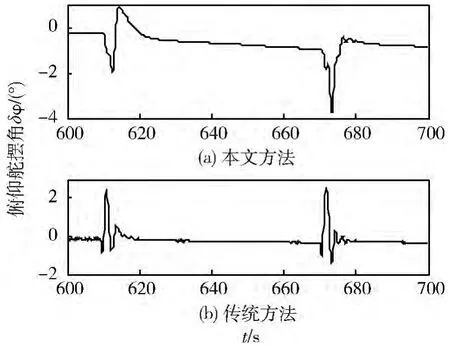
图8 俯仰舵摆角

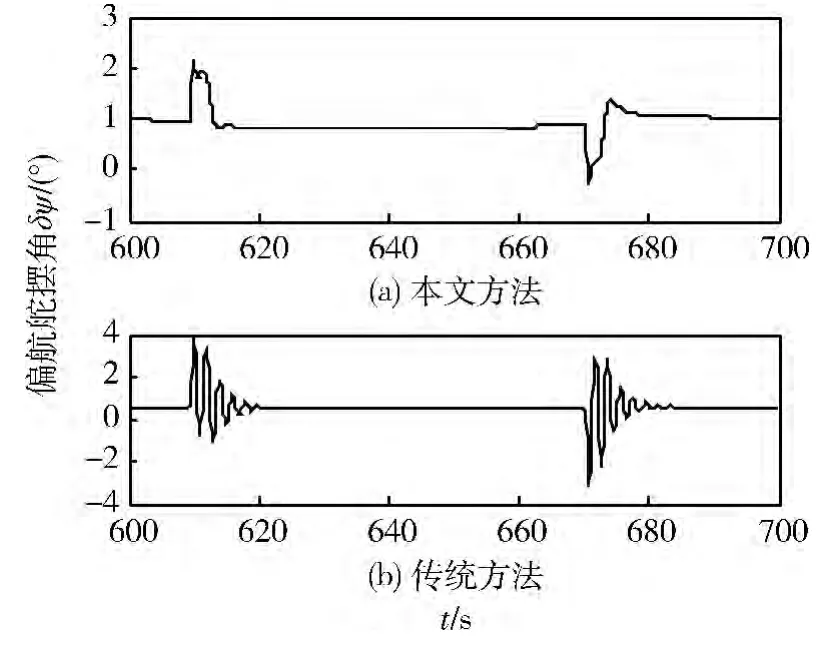
图9 偏航舵摆角

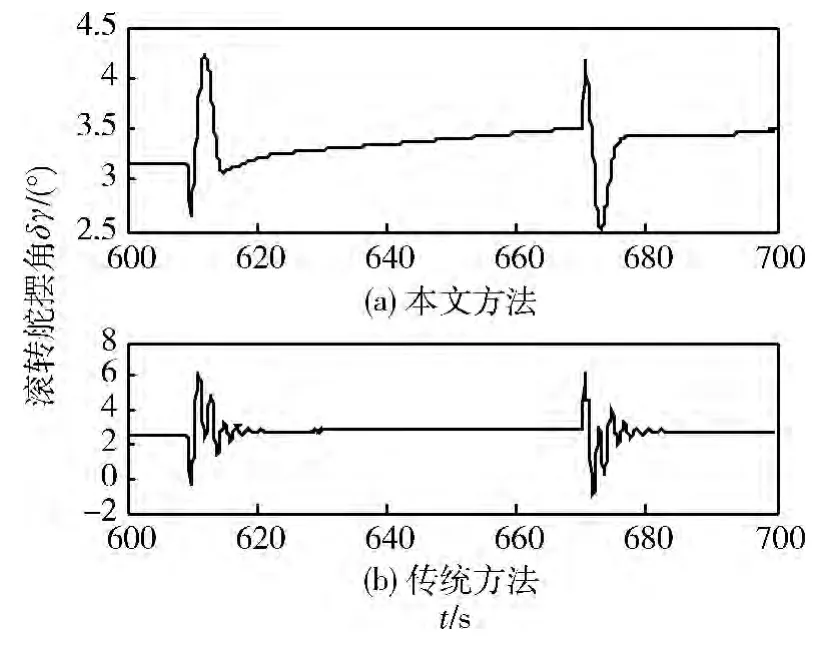
图10 滚转舵摆角

4 结论

建立了高超声速滑翔飞行器非线性姿态控制系统数学模型，把外部不确定扰动作为一种有界干扰，将滑模变结构控制思想与Lyapunov 稳定性理论相结合设计了一种变结构控制器和外部干扰界值的在线估计自适应律，该方法可以对外界不确定干扰进行有效的抑制补偿，比传统的控制方法具有更高的跟踪精度，更强的鲁棒性，过渡过程平滑，在大攻角大滚转角情况下解决了BTT 控制3通道强耦合问题，设计方法简单易于理解，易于工程实现。

［1］遆晓光，孔庆霞，余颖. 基于自适应动态逆的高超声速飞行器姿态复合控制［J］.宇航学报，2013，34(7):955-962.(DI Xiaoguang，KONG Qingxia，YU Ying. Attitude control for hypersonic vehicle with compound actuators based on adaptive dynamic inversion［J］. Journal of Astronautics，2013，34(7):955-962.)

［2］Bhandari S，Raheja A，Tang D，et a1.Modeling and control of UAVs using neural networks［C］.AIAA Modeling and Simulation Technologies Conference，Minneapolis，USA，August 13—16，2012.

［3］高道祥，孙增圻.高超声速飞行器离散模糊自适应控制［J］. 空间控制技术应用，2009，35(5):13-19.(GAO Daoxiang，SUN Zengqi. Discrete-time fuzzy adaptive control for the hypersonic aircraft［J］. Aerospace Control and Application，2009，35(5):13-19.)

［4］庄开宇，张克勤，苏宏业，褚健.高阶非线性系统Terminal 滑模控制［J］.浙江大学学报，2002，36 (5):482-485. (ZHUANG Kaiyu，ZHANG Keqin，SU Hong ye，CHU Jian. Terminal sliding mode control for highorder nonlinear dynamic systems［J］. Journal of Zhejiang University，2002，36 (5):482-485.)

［5］吴立刚，王常虹，曾庆双.Terminal 滑模自适应控制实现一类不确定混沌系统的同步［J］. 控制与决策，2006，21 (2):229 － 232. (WU Ligang，WANG Changhong，ZENG Qingshuang. Synchronization of chaotic systems with parametric uncertainty using terminal sliding mode adaptive control［J］. Control and Decision，2006，21 (2):229-232.)

［6］王志，周军，周凤岐. 低速滚转弹道导弹运动模型及变结构姿态控制系统设计［J］. 兵工学报，2007，28(7):849-853. (WANG Zhi，ZHOU Jun，ZHOU Fengqi. Movement model and design of variable structure attitude control system for low speed spinning ballistic missiles［J］. Acta Armamentarii，2007，28(7):849-853.)

［7］佘文学，周凤岐，周军.非线性变结构制导律［J］. 宇航学报，2003，24(6):638-641. (SHE Wenxue，ZHOU Fengqi，ZHOU Jun. Nonlinear variable structure guidance law［J］. Journal of Astronautics，2003，24(6):638-641.)

［8］佘文学，周凤岐，周军. 一类不确定非线性系统变结构自适应鲁棒控制［J］.西北工业大学学报，2004，22(1):25-28.(She Wenxue，Zhou Fengqi，Zhou Jun. A control algorithm for designing anti-ballistic missile Terminal Guidance Law［J］. Journal of Northwestern Polytechnical University，2004，22(1):25-28.)

［9］孙彪，孙秀霞.基于干扰观测器的离散滑模控制算法［J］. 控制工程，2010，17(4):440-443. (SUN Biao，SUN Xiuxia. Discrete-time Sliding Mode Control Algorithm Based on Disturbance Observer［J］. Control Engineering of China，2010，17(4):440-443.)

［10］韩京清.自抗扰控制技术(估计补偿不确定因素的控制技术)［M］. 北京:国防工业出版社，2008. (HAN Jingqing. Active Disturbance Rejection Control Technique(The Technique for Estimating and Compensating the Uncertainties)［M］. Beijing:National Defense Industry Press，2008.)

［11］孙彪，孙秀霞，陈琳，等.基于幂次函数的离散滑模控制算法［J］. 控制与决策，2013，26(2):285 －288.(SUN biao，SUN Xiu － xia，CHEN Lin，et al. Algorithm of discrete － time sliding mode control based on power－function［J］. Control and Decision，2013，26(2):285 －288.)