在轨服务飞行器对共面圆轨道目标接近过程分析

李 岩 姚静波 辛朝军 苏宪程

1.装备学院航天装备系，北京101416

2.装备学院训练部，北京101416

在轨服务飞行器(On-Orbit Service Vehicle，OSV)与目标航天器的互相接近是实施在轨服务的必要前提，合理选择接近过程中的机动策略能保证2个航天器高效、安全、可靠地实现轨道交会和相互联接。

文献［1］针对航天器大范围轨道交会，关注能耗因素，提出了二冲量燃料最省机动方案的数值寻优算法。文献［2］考虑2个航天器距离及飞行时间等因素，研究了非开普勒轨道上追踪卫星的交会变轨决策问题，提出解决该问题的近似求解方法。文献［3］提出了一种半解析的快速设计算法，设计了连续小推力发动机实现的调相机动。可见，追踪航天器(OSV)和目标航天器的轨道高度、相对位置，机动过程方式、时间和能耗等因素都是研究大范围轨道机动设计的关键环节。文献［1 －3］从各自关注的重点出发提出了有效解决问题的方法和思路，但在机动策略的选择，以及综合分析诸多因素的相互影响等方面考虑得还不够全面。本文将逐步分析时间、相位调整、能耗和轨道配置等两航天器接近过程中的多种因素及其相互影响，提出更加全面的轨道机动策略选择依据。

1 轨道转移相位分析

同轨道交会过程相似，OSV 首先实施大范围、远距离的轨道机动，沿霍曼椭圆过渡轨道运行至比目标轨道低数十公里(30 ～50 km)的圆形停泊轨道，为实施下一步自主导引接近提供条件［4－5］。在此过程中，OSV 的轨道机动等效为两共面圆轨道间的轨道转移问题。

为了节省OSV 的能耗，变轨过程采用霍曼转移方式。在变轨发动机点火前，OSV 需要完成轨道相位的调整，使2个航天器的地心角之差满足霍曼转移的相位差θH，即满足交会窗口条件，保证2个航天器在指定的时刻和位置相互接近。

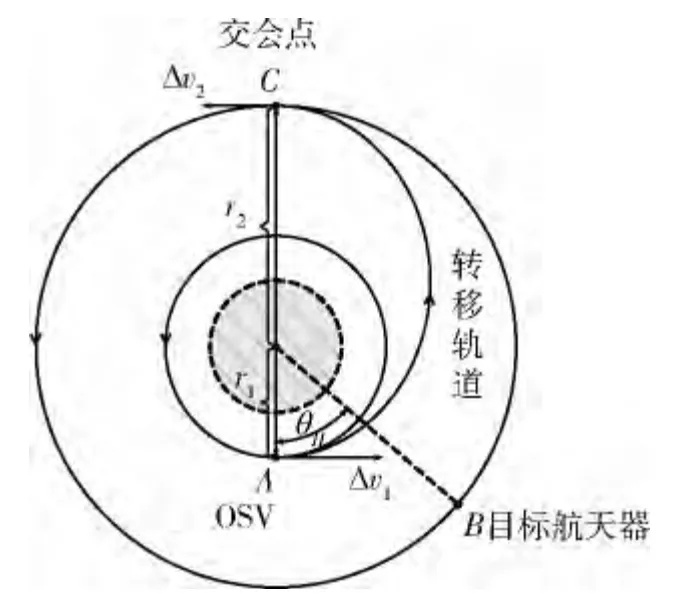
图1 霍曼转移轨道示意

由图1 中的位置关系可以得到:

得到霍曼转移相位差:

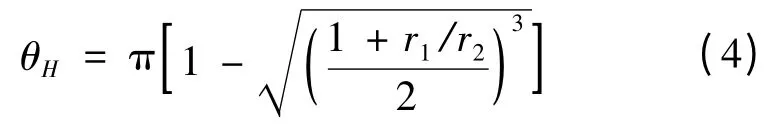
式中，TH和T2分别为霍曼转移轨道周期和目标航天器轨道周期;r1和r2分别为OSV 待机轨道半径和目标轨道半径。

由于目前在轨服务活动主要在地球同步轨道以内的空间实施，所以r1最小可近似取地球半径6378.14km，r2最大可取同步轨道半径42164. 17 km，即0.1512 ＜(r1/r2)＜1 。图2 中给出了相应的霍曼转移所需相位差与r1/r2的关系，可见0° ＜θH＜110° 。在近地轨道范围(200 km ～2000 km)，0.7 ＜(r1/r2)＜1 ，则0° ＜θH＜40° 。

2 轨道转移前的相位调整过程

如果初始时刻目标航天器和OSV 之间的轨道相位差不是θH，而是θH+Δθ(0 ≤Δθ ＜2π)，就不能立即执行霍曼转移(如图3)。否则当OSV 达到交会点时，目标航天器与交会点之间将有一个角度差Δθ。

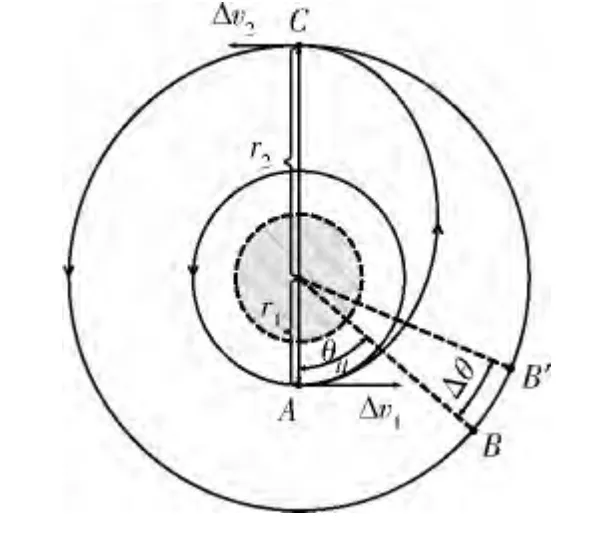
图3 轨道相位不满足霍曼转移相位示意

由于内圆轨道的角速度ω1大于外圆轨道的角速度ω2，所以，角度差可以通过自然调相消除［6］。设调节时间为tω，则:

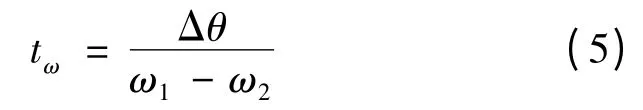
交会总时间t 是霍曼转移时间tH和等待时间tω之和:

当然轨道相位的调整也可以采用速度调相的方法(如图4)。在共轨速度调相中，OSV 可以通过2次大小相等方向相反的速度增量，经与初始轨道相切的椭圆调相轨道，在预定时间内从原位置A 到达新的位置B。图4 中(a)和(b)分别是A 点超前和滞后于B 点时的调相轨道。

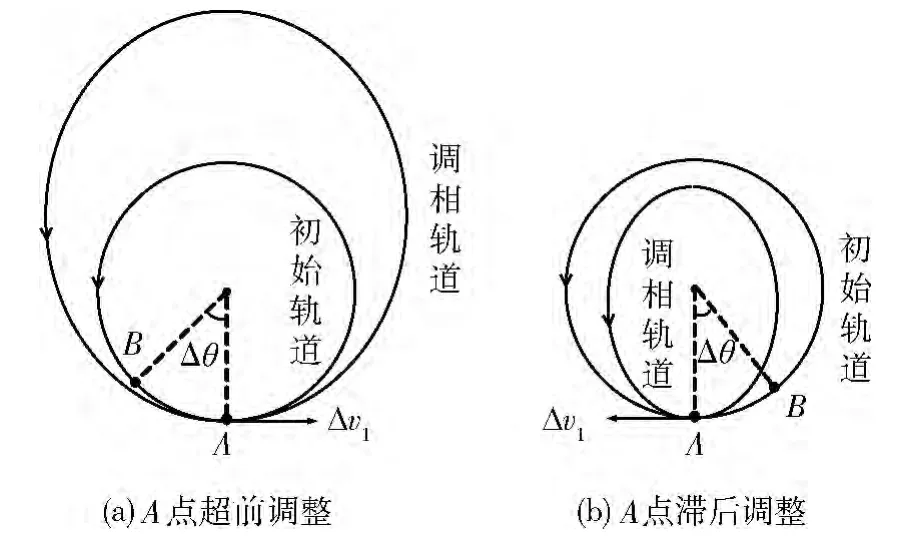
图4 共轨速度调相示意

设初始圆轨道半径为r，轨道周期为Tr，速度为vr。图4(a)中，在A 点向前进方向施加速度增量Δv1，进入调相椭圆轨道的近地点，设近地点速度为vp，调相轨道半长轴为a，周期为Ta，则有:

图4(b)中，在A 点向与前进方向相反的方向施加速度增量Δv1，进入调相椭圆轨道的远地点，设速度为va，调相轨道半长轴为a，周期为Ta，则:

此时，由于a ≥(re+r)/2，那么Δθ 有最大值，即:

相应的调相时间有最小值限制:

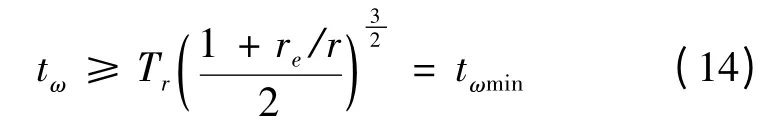
图5 给出了初始轨道高度在200 km ～2000km的低轨范围内变化时，共轨速度调相所需的速度增量和时间随相位差的变化曲线。图5(a)中，速度增量和调相时间均随相位差的增大而增大;速度增量随高度的增加而减小，调相时间则随高度的增加而增加。图5(b)中，不同的轨道高度对应不同的最大可调相位差，因此相位差的取值范围随高度增加而增加。在可调相位差的公共区域进行比较，如0° ～50°之间，速度增量随相位差的增加而增大，但调相时间则相反;速度增量随高度的增加而减小，调相时间随高度增加而增加。对比2个图可以看出，在近地轨道区域进行速度调相，超前或滞后相位差在0°～50°之间时，均可实现调相。在此区间内，速度增量需求随高度变化不明显，而且不大于0.5km/s。

为比较速度调相和自然调相的特点，以具体算例进行分析。设目标轨道为400km，OSV 待机轨道低于目标轨道，在100km ～400km 之间取值，相位差在超前或滞后0° ～50°之间变化，分析OSV 采取速度调相和自然调相所需时间的变化情况。

图6 给出了算例中速度调相时间随轨道高度的变化曲线，图6(a)中可以看出，超前调相时间大于待机轨道周期Tr，随着高度和相位差的增加而增加，且线性特点明显。图6(b)中滞后调相时，所需时间随相位差的增加而减小，也就是说，相位差越小，调相时间反而长。由于最大可调相位差的限制，在相位差增大到一定数值时，轨道高度低于170km 的待机轨道无法满足调相要求，变化曲线呈现非线性。在可调相位区间，调相时间小于待机轨道周期Tr。

图7 给出了算例中自然调相时间随轨道高度变化曲线，由于自然调相的单向性特点，OSV 超前相位差Δθ，等同于滞后360° － Δθ。可见调相时间随高度变化呈现非常明显的非线性。特别是在待机轨道高度与目标轨道高度相差较小时，调相时间随相位差的增加而急剧增加。但在轨道高度较低，滞后相位差较小的区域，变化呈近似线性，且调相时间无最小值限制。因此，增大轨道高度差，且使OSV 处于相位差较小的滞后状态，有利于减少自然调相时间。

图5 不同轨道高度，共轨调相速度增量和调相时间随相位差变化曲线族

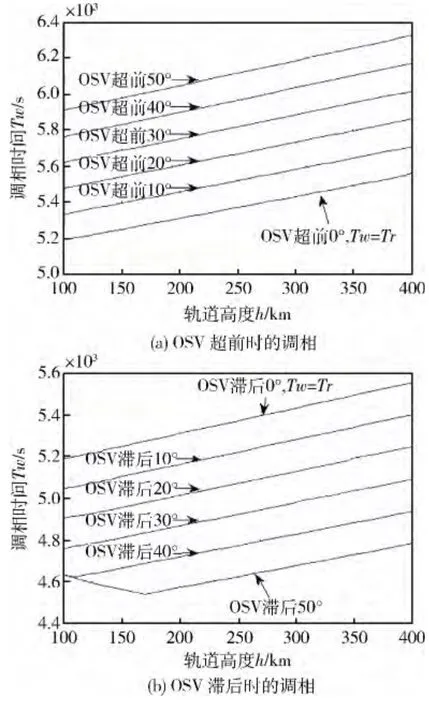
图6 相位差不同时，速度调相时间随待机轨道高度变化曲线族

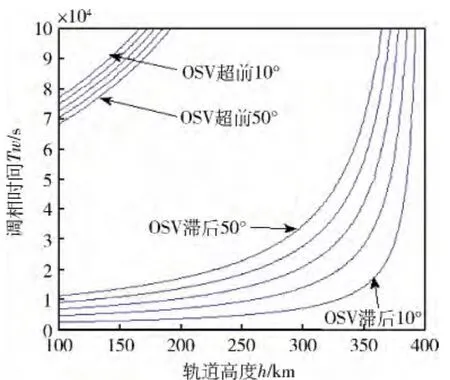
图7 相位差不同时，自然调相时间随待机轨道高度变化曲线族

表1 给出了自然调相和速度调相的特点对比。

由于OSV 机动能力有限，在执行交会对接任务时，为了减少OSV 的燃料消耗，尽可能采用自然调相的方法，待机轨道以及相位差的选择应适合自然调相的条件要求。

表1 自然调相和速度调相特点对比

3 轨道转移的速度增量

采用自然调相的前提下，轨道转移的速度增量即为霍曼转移所需的速度增量，为图1 中Δv1与Δv2之和［7－8］。设霍曼转移轨道近地点速度大小为vp，远地点速度大小为va，初始轨道速度大小为v1，目标轨道速度为v2，则

4 综合算例分析

设目标轨道高度h2为400km，轨道倾角51.65°。OSV 的待机轨道倾角和升交点位置应选择与目标轨道一致，以减少轨道平面机动带来的燃料消耗。轨道高度h1成为待机轨道选择的可变因素。

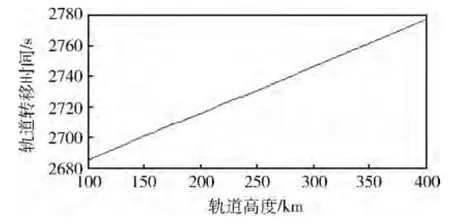
图8 OSV 初始轨道高度h1 与轨道转移时间tH 的关系

图8 给出了OSV 初始轨道高度h1从100km ～400km 区间变化时，轨道转移时间tH的变化趋势。轨道高度越高所需转移时间也相应增加，从节省时间角度应当选取较低的初始轨道。

图9 给出了OSV 初始轨道高度h1从100km 到400km 区间变化时，轨道转移所需的速度增量之和Δv 的变化趋势。轨道高度越高，Δv 越小，从减少在轨系统能量消耗的角度应选择轨道较高的初始轨道。

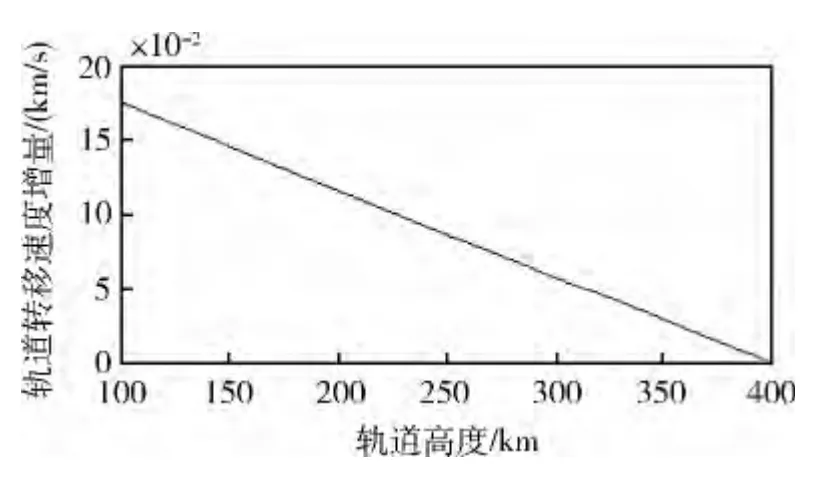
图9 OSV 初始轨道高度h1 与轨道转移总的速度增量Δv 之间的关系

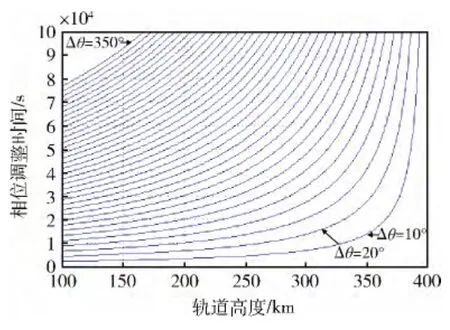
图10 初始相位差不同时，OSV 初始轨道高度h1调相所需时间tω 的关系

图10 和11 分别给出了OSV 初始轨道高度h1从100km 到400km 区间变化时，采用自然调相法，调整相位偏差Δθ 所需时间的变化趋势，以及轨道转移总时间的变化趋势。可以看出，在OSV 滞后相位差Δθ ＜10°，轨道高度h1＜250km 的区域，调相时间随待机轨道高度变化比较平缓，呈近似线性。在此区域，尽可能减小OSV 的滞后相位差，能够缩短调相时间。

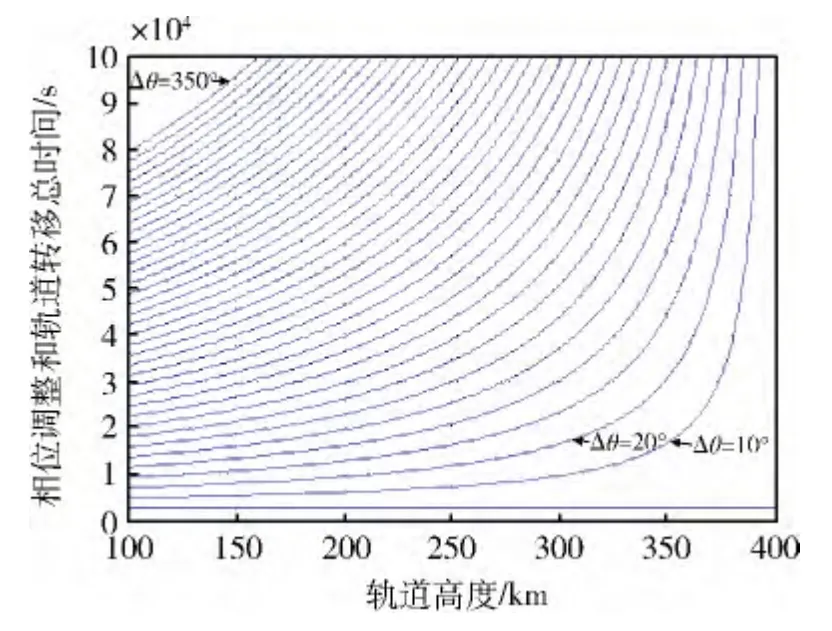
图11 初始相位差不同时，OSV 初始轨道高度h1 与调相和转移总时间tH + tω 的关系

从上述轨道高度与时间以及速度增量关系的分析可见，机动飞行器选择200 km ～250 km 的初始轨道，在减少燃料消耗和缩短机动时间方面取得了较好的效果。

5 结论

为节省OSV 燃料消耗，大范围轨道交会一般采用霍曼转移方式，针对具体任务合理选择待机轨道、停泊轨道、初始相位差、变轨时机和交会时间等参数:待机轨道平面与目标轨道平面一致，轨道高度需要留有一定的高度差用于相位调整;尽量采用自然调相的方式，OSV 初始相位应滞后于目标且角度较小为宜;调相到达霍曼转移相位差时为最佳变轨时机;在节省能量的前提下机动和调相总时间越小越好。

上述研究基于二体问题动力学模型，没有充分考虑轨道摄动等多种影响因素，此外还有较多需要进一步完善的方面，如:算例仅针对低轨目标，需要进一步充实;机动过程采用OSV 主动接近方式，还可考虑双主动接近策略;机动模型仅考虑较常用的双脉冲机动，需要深入分析对比如多脉冲机动、连续推力机动等其它机动方式等。

［1］丁濛，童若锋，董金祥. 大范围轨道机动的燃料消耗优化方法［J］. 航天控制，2008，26(6):47-53. (DING Meng，TONG Ruofeng，DONG Jinxiang. Optimization methods for fuel consumption in large-scale spacecraft orbit maneuver［J］. Aerospace Control，2008，26(6):47-53.)

［2］张拓，高晓光，樊昊. 非开普勒轨道下卫星交会变轨决策 研 究［J］. 航 天 控 制，2012，30 (2):51-56.(ZHANG Tuo，GAO Xiaoguang，FAN Hao. The study on decision-making of the maneuver in satellite orbits based on non-Keplerian［J］. Aerospace Control，2012，30(2):51-56.)

［3］王帅，尚海滨，崔平远，黄翔宇.小推力地球卫星圆轨道同轨调相设计方法研究［J］. 宇航学报，2013，34(1):1-8. (WANG Shuai，SHANG Haibin，CUI Pingyuan，HUANG Xiangyu. Study on design method of low-thrust phasing maneuvers for earth circle-orbit satellites［J］. Journal of Astronautics，2013，34(1):1-8.)

［4］李岩，蔡远文.多目标群的在轨服务飞行器部署策略［J］.哈尔滨工程大学学报，2012，33(4):459-463.(LI Yan，CAI Yuanwen. The deployment of orbital servicing vehicles for multi-targets［J］. Journal of Harbin Engineering University，2012，33(4):459-463.)

［5］王佳，于小红.轨道机动作战中的待机轨道研究［J］.航天控制，2005，23(5):17 ～22. (WANG Jia，YU Xiaohong. Research on parking-orbit in orbit maneuvering operation［J］. Areospace Control，2005，23 (5):17-22.)

［6］朱仁璋.航天器交会对接技术［M］. 北京:国防工业出版社，2007.

［7］敬忠良，袁建平，罗建军，等.航天器自主操作的测量与控制［M］.北京:中国宇航出版社，2011.

［8］刘暾，赵钧.空间飞行器动力学［M］.哈尔滨:哈尔滨工业大学出版社，2003.