二维数字匹配滤波的信噪比分析
龙 杰 李聪欣 蒋 超 赵 君
1.信息系统工程重点实验室,北京100038
2.北京理工大学,北京100081
合成孔径雷达(Synthetic Aperture Radar,SAR)是一种同时使用脉冲压缩和合成孔径技术的雷达[1-2],它在距离向脉冲压缩处理的信噪比增益为时宽带宽积,在方位向的处理增益为合成孔径处理增益,SAR 合成孔径时间Ta内相干积累了n个回波信号,从相参积累的角度看,方位向处理的信噪比增益为脉冲重复频率和形成合成孔径所需时间的乘积[3-4];但是,从匹配滤波的角度看,SAR 方位向处理也等价于匹配滤波的过程,那么信噪比增益为方位向信号的多普勒带宽与积累时间的乘积[5]。从这一点看,目前存在2 种关于SAR 信噪比增益的计算方法[6-8],但会产生不同的计算结果。因此,需要对SAR 两维信号处理的信噪比增益进行分析。
另外,当雷达系统需要接收多种不同带宽信号时,若信号带宽的覆盖范围很大,为减少硬件资源和降低系统复杂度,接收机设计的滤波器往往需要按照接收信号的最大带宽选择。当接收小带宽信号时,噪声带宽往往会大于信号带宽,在这种条件下,需要对信号处理后的信噪比增益进行分析,因此需要分析不同噪声带宽下的SAR 信噪比增益,对采样率进行优化设计。
本文主要针对SAR 信号处理的特点,首先从连续信号匹配滤波的过程出发,推导了数字匹配滤波的信噪比增益;其次对SAR 二维匹配滤波处理的信噪比增益展开数学分析;最后通过仿真试验验证了本文理论分析的正确性,解决了SAR 信噪比增益的争议问题。
1 数字匹配滤波的信噪比增益
设匹配滤波器的输入信号为s(t),其对应的频谱S(f)可以表示为:
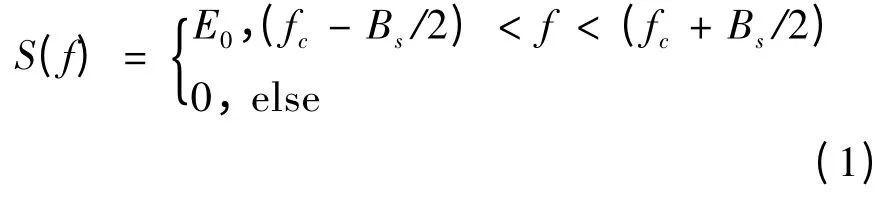
式中,E0为信号频谱的幅度;Bs为信号带宽;fc为中心频率。
设输入的随机噪声为平稳的带限白噪声,其功率谱可以表示为:

式中,N0为功率谱密度;Bn为噪声带宽。则输入的噪声功率为:
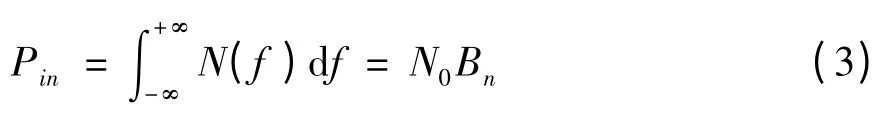
那么经过匹配滤波器H(ω)= S*(ω)后,匹配滤波的信噪比增益可表示为:

式中,SNRo为输出信噪比;SNRi为输入信噪比。信号的能量Ep可以表示为:
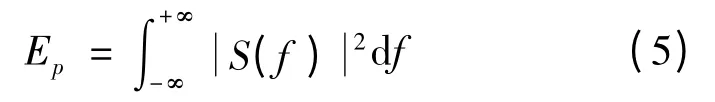
在连续时间信号条件下,式中的信噪比增益可以表示为:
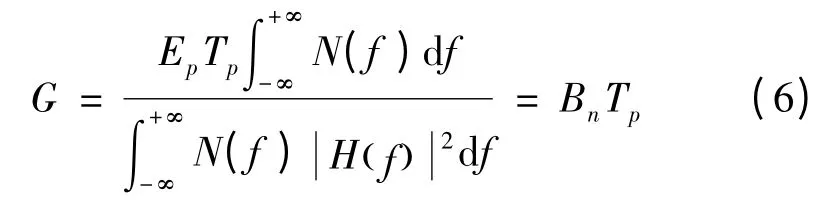
当输入的连续随机噪声经过数字采样后,白噪声会变为色噪声,噪声的功率谱会随采样率的变化而变化。下面讨论采样率对功率谱的影响,根据随机过程的采样定理[9],得到离散后的信噪比增益为:

式中,fs为信号的采样率。式中的分子求和项表示采样后的输入噪声功率,分母求和项表示匹配滤波后的输出噪声功率,令

令x = (f - nfs)/fs,则输入噪声功率为:

式中,

同理,可得输出噪声功率为:

下面主要针对不同的噪声带宽Bn、采样率fs和信号带宽Bs,对信噪比增益展开分析:
(1)若Bn/2fs≤1/2 ,即fs≥Bn≥Bs

从而可以得到信噪比增益为:
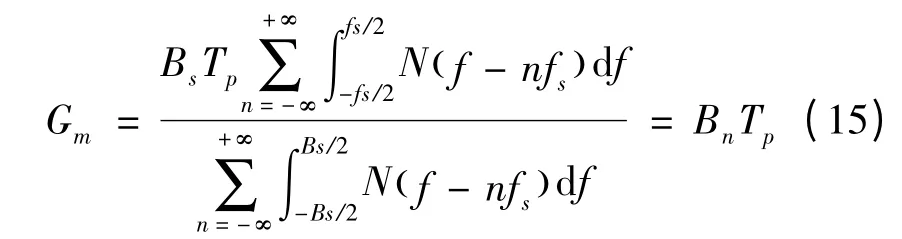
从上式可以看出,当满足条件(1)的关系式时,匹配滤波的信噪比增益为噪声带宽与信号时宽的乘积,只不过通常在雷达接收端的滤波器带宽与信号带宽近似相等[10],可以认为信噪比增益为信号的时宽带宽积。
然而,当雷达系统需要接收多种不同带宽的信号时,若信号带宽的覆盖范围很大,为了减少硬件资源和降低系统复杂度,接收机的滤波器往往需要按照信号的最大带宽选择。当接收小带宽信号时,噪声带宽会大于信号带宽,因此需要分析不同条件下的信噪比增益。
(2)若Bn/2fs>1/2 ,即Bn≥fs≥Bs
设p = [Bn/2fs+1/2 ],其中,[·]表示取整数部分,q = Bn/2fs+1/2 -p,则式(15)中的分母求和项中共含有2p +1个积分区间,其中包括2p - 1个完整积分区间和2个非完整积分区间。
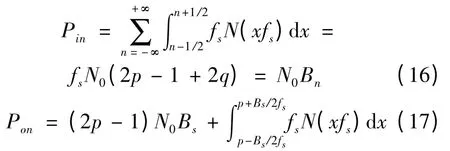
其中,对式(17)中的输出噪声功率需要根据噪声带宽、信号带宽和采样率三者之间的关系,分下面3 种情况进行讨论:



从而可以得到离散采样后匹配滤波的信噪比增益为:

从上面分析可以看出,数字匹配滤波的信噪比增益由噪声带宽Bn、采样率fs和信号带宽Bs的相对关系共同决定。传统的计算SAR 距离向处理信噪比增益是在fs≥Bn≥Bs条件下得到的[11],它只与时宽带宽积有关,而在Bn≥fs≥Bs的多种信号带宽条件下不再适用,本文给出了该条件下的解析表达式,能够计算不同噪声带宽条件下的信噪比增益。从式(21)可以看出,当时,Gm= fsTp,即当采用低采样率对噪声进行采样时,信噪比增益会相应减小;当1,2,…时,信噪比增益可以取得周期性极大值,此时如当n = 0 时,即满足关系时,信噪比增益可以达到最大值。
2 二维匹配滤波的信噪比增益
SAR 成像过程实质上是一个二维匹配滤波过程,为了处理和实现方便,一般都是通过数据采集,在数字域实现二维匹配滤波。根据前面分析的结论,距离向匹配滤波的信噪比增益为:

同理,方位向匹配滤波的信噪比增益为:
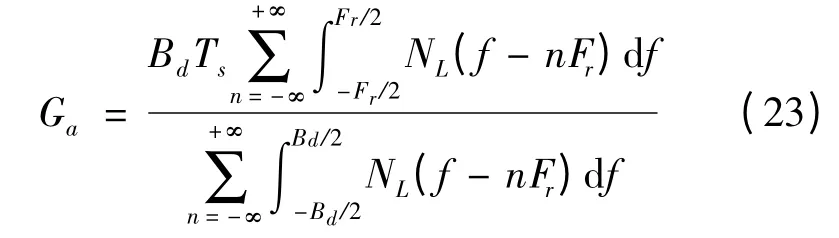
式中,Fr为脉冲重复频率,即方位向采样率;Bd为方位向多普勒带宽,Ts为方位向积累时间。则二维匹配滤波的信噪比增益可以表示为:
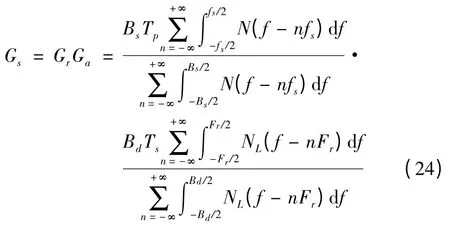
由于方位向匹配滤波处理前,输入的噪声功率为距离向处理后的输出噪声功率,根据前面的推导可知,采样后噪声功率保持不变,则有:

因此可以得到:

即:

当进行方位向匹配滤波时,与距离向匹配滤波进行类比,可以认为输入的噪声带宽为Bs,采样率为Fr,方位向信号带宽为Bd。同理可设k = [Bs/2Fr+1/2 ],l = Bs/2Fr+1/2 - k。由前面数字匹配滤波推导的结论可知,式(27)中的分母可以表示为:
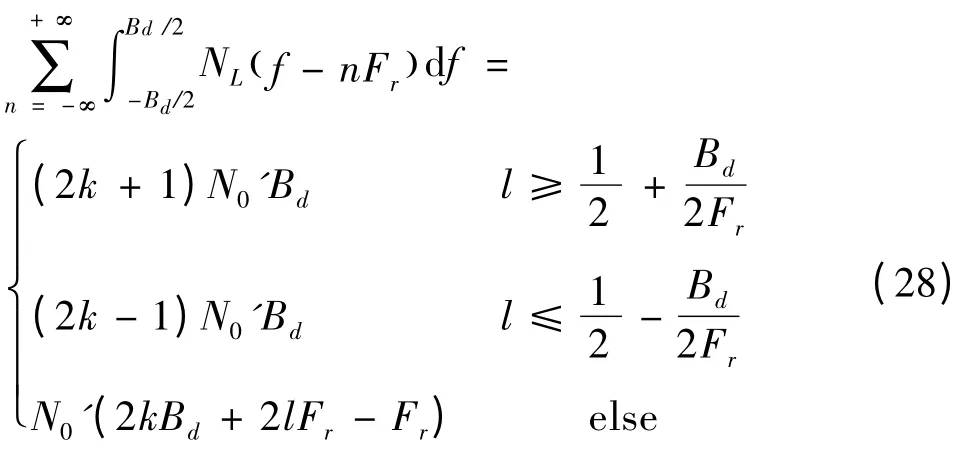
其中,N0'为方位向处理前的等效噪声功率谱。由于距离向处理完成后,噪声带宽被限制在信号带宽Bs内,则等效噪声功率谱为:

联合式(27)、(28)和(29)可以得到二维匹配滤波的信噪比增益为如下3 种情况:



当Bs>>Fr≥Bd时,信噪比增益可以近似为:
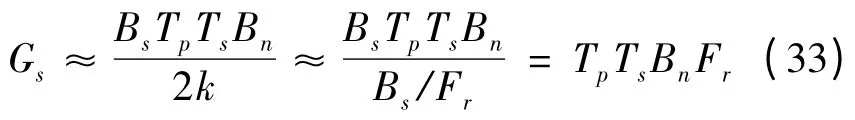
从式(33)可以看出,传统计算SAR 的二维处理增益只是在该条件下的一种近似,它与多普勒带宽无关,但从匹配滤波的角度看,却与多普勒带宽有关。针对该计算结果,本文给出的SAR 二维信噪比处理增益的表达式可以计算任意参数配置条件下的处理增益,从式(30)~(32)可以看出,二维匹配滤波的信噪比增益与信号带宽、信号时宽,多普勒带宽、积累时间、噪声带宽、采样率及Fr都有关,需要根据具体参数精确计算SAR 信噪比增益。
3 仿真分析
在表1 所示的系统参数条件下,对数字匹配滤波处理的信噪比增益进行仿真。
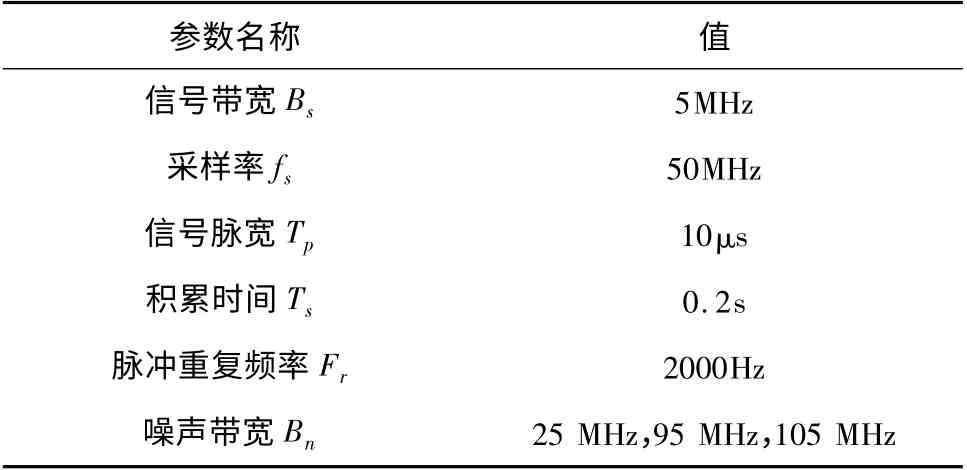
表1 系统参数
采用理论计算的方法,可以得到匹配滤波的信噪比增益与噪声带宽的关系如图1 所示,从中可以看出,当噪声带宽满足2nfs+Bs≤Bn≤2(n +1)fs- Bs时,信噪比增益随噪声带宽单调递增;当2(n +1)fs- Bs≤Bn≤2(n +1)fs+ Bs时,信噪比增益随噪声带宽单调递减,而传统计算方法与噪声带宽只呈单调的线性关系。本文在离散的带限白噪声条件下,匹配滤波的信噪比增益随噪声带宽呈现出周期性变化,并且可以取得周期性极大值。
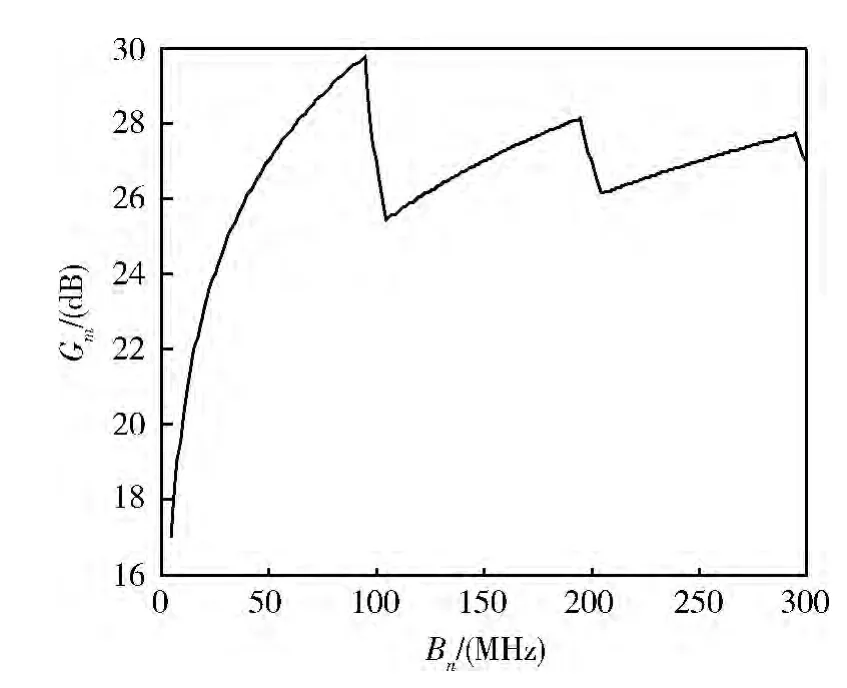
图1 一维匹配滤波信噪比增益与噪声带宽的关系
采用蒙特卡洛仿真的方法验证理论推导结果,在试验次数为5000 次的条件下,匹配滤波的信噪比增益的仿真结果如图2 所示,信噪比增益取多次试验结果的平均值,表2 给出了在不同噪声带宽条件下,匹配滤波信噪比增益的仿真结果与理论计算值的对比。由于噪声具有统计特性,理论值与仿真结果基本相吻合,从而验证了理论推导的正确性。其中,当噪声带宽Bn=95MHz 时,信噪比增益达到最大,此时满足Bn= 2fs-Bs的关系,这与式的理论计算结果一致。另外,当系统噪声带宽和信号带宽一定时,也可以通过合理地选择采样率使系统的输出信噪比达到最优,即最佳采样率可以设计为f*s=
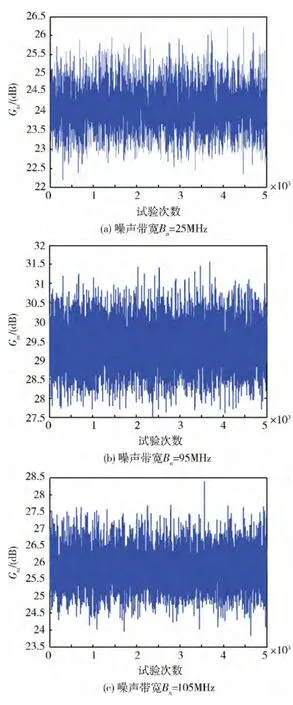
图2 不同噪声带宽条件下的信噪比增益
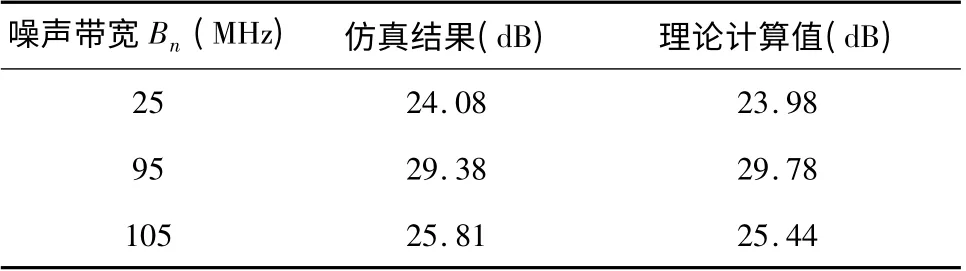
表2 信噪比增益
下面对二维匹配滤波的信噪比增益进行仿真,如图3 所示,从中可以看出,二维匹配滤波的信噪比增益随噪声带宽也呈周期性变化,表3 给出了在不同噪声带宽条件下二维匹配滤波信噪比增益的仿真结果与理论计算值的对比。从表3 可以看出,当噪声带宽Bn= 2fs- Bs=95MHz 时,二维匹配滤波的信噪比增益达到最大值。传统计算方法只与信号时宽、噪声带宽、脉冲重复频率和积累时间有关,而本文方法还与采样率、多普勒带宽等参数相关,验证了在不同噪声带宽和多普勒带宽条件下的信噪比增益,并为SAR 采样率优化设计提供了准则。

图3 二维匹配滤波信噪比增益与噪声带宽的关系

表3 二维匹配滤波信噪比增益
从图4(a)可以看出,在不同的多普勒带宽条件下,信噪比增益随PRF 的增加而逐渐增大,相对传统计算方法与多普勒带宽无关而言,从图4(b)的局部放大图中可以看出,信噪比增益与PRF 成正相关,并在大多普勒带宽条件下这种影响尤为明显。

图4 二维匹配滤波的信噪比增益与PRF 的关系
4 结论
根据理论分析和仿真结果可知,离散采样会导致白噪声变为色噪声,在色噪声条件下,二维匹配滤波器的信噪比增益与噪声带宽、脉冲重复频率、信号带宽和采样率的相对关系有关,当满足一定条件时,它与传统匹配滤波的信噪比增益等价。其次,在离散带限白噪声条件下,通过分析噪声带宽对信噪比的影响,信噪比增益会出现周期性极大值,当采样率、噪声带宽和信号带宽满足条件时,匹配滤波的信噪比增益达到最大,可以基于信噪比最大准则对SAR 采样率进行优化设计。
[1]Li Zengliang,Zhao Xin,Ding Zegang. Analysis of diving squint SAR resolution[C]. Proceedings of 2011 IEEE CIE International Conference on Radar,Chengdu,2011:875-878.
[2]Hu Cheng,Long Teng,Zeng Tao,et al. The accurate focusing and resolution analysis method in geosynchronous SAR[J]. IEEE Transactions on Geoscience and Remote Sensing,2011,49(10):3548-3563.
[3]皮亦鸣,杨建宇.合成孔径雷达成像原理[M].成都:电子科技大学出版社,2007:22-30. (PI Yiming,YANG Jianyu. Principle of Synthetic Aperture Radar Imaging[M]. Chengdu:Press of the University of Electronic Science and Technology,2007:22-30.)
[4]袁孝康.星载合成孔径雷达导论[M]. 北京:国防工业出版社,2003.(YUAN Xiaokang. Introduction to the Spaceborne Synthetic Aperture Radar[M]. Beijing:National Defense Industry Press,2003)
[5]仇晓兰,丁赤飚,胡东辉. 双站SAR 成像处理技术[M]. 北京:科学出版社,1993.(QIU Xiaolan,DING Chibiao,HU Donghui. The Bistatic SAR Imaging Processing Technology[M].Beijing:Science Press,1993.)
[6]Jiang Chenglong,Jiang Hai,Zhang Bingchen,Hong Wen,Wu Yirong. SNR analysis for SAR imaging from raw data via compressed sensing[C]. Proceedings of 9th European Conference on Synthetic Aperture Radar,Hamburg,Germany,2012:689-692.
[7]Jiang Chenglong,Zhang Bingchen,Zhang Z,Hong W,Wu Yirong. Experimental results and analysis of sparse microwave imaging from spaceborne radar raw data[J].SCIENCE CHINA Information Sciences,2012,55(8):1801-1815.
[8]Raney R K. SNR IN SAR[C]. Proceedings of IEEE IGARSS’85,USA,1985:994-999.
[9]朱华,黄辉宁,等. 随机信号分析[M]. 北京:北京理工大学出版社,2006. (Zhu Hua,Huang Huining.Random Signal Analysis[M]. Beijing:Press of Beijing Institute of Technology,2006.)
[10]张群英,杨学贤,韩月秋. 数字匹配滤波系统输出信噪比与采样速率的关系[J]. 系统工程与电子技术,1999,21(10):63-65.(Zhang Qunying,Yang Xuexian,Han Yueqiu. Relation of Sampling Rate and SNR in Digital Matched Filter System[J]. Systems Engineering and Electronics,1999,21(10):63-65.)
[11]万永伦,姒强,吕幼新,王洪,汪学刚. 宽带信号去斜脉冲压缩处理方法的研究[J]. 航空学报,2006,27(5):917-921. (Wan Yonglun,Si Qiang,Lv Youxin,Wang Hong,Wang Xuegang. Study of dechirp pulse compression processing method for wideband signals[J]. Acta Aeronautica et Astronautica Sinica,2006,27(5):917-921.)

