三阶实对称矩阵正交对角化的简便方法＊

林 林，欧阳成

（湖州师范学院 理学院，浙江 湖州313000）

0 引言

实对称矩阵的对角化是高等代数的重要研究内容，其计算量较大.很多数学研究工作者对此做了大量研究，并提出了不同的求解方法简化计算过程.如由解方程组求实对称矩阵的正交特征向量将实对称矩阵对角化［1］；利用合同变换和相似变换将实对称矩阵对角化［2］；利用Householder变换直接将实对称矩阵对角化［3］；黄泽霞等［4］利用实对称矩阵的一个性质，找到了一个求其特征向量的简便方法；李蕊［5］通过简单的初等行变换求出实对称矩阵的两两正交的特征向量，从而得到将实对称矩阵正交相似对角化的简便方法；顾央青［6］通过解方程组直接求出矩阵A的正交特征向量；李先明［7］给出了用行初等变换化实对称矩阵为对角形的方法.

本文主要研究三阶实对称矩阵A＝（aij）3×3（aij＝aji）有二重特征值时的正交对角化问题，利用属于相异特征值的特征向量互相正交的几何特征，给出快速求解正交矩阵Q，使得Q－1AQ＝Q′AQ＝diag（λ1，λ2，λ3）为对角矩阵，其中λ1（＝λ2）与λ3为三阶实对称矩阵两个相异的特征值.在高等代数中求正交变换将实二次型化为标准形，以及在解析几何中化简某些二次曲面方程，其本质与三阶实对称矩阵的正交对角化问题是一样的.所以，此简便方法也可以应用于这些题型.对于A有三重特征值或三个彼此相异特征值的情形，这种正交矩阵Q的选取相对较简单，本文对此不作讨论.

1 正交对角化方法及其理论证明

1.1 正交对角化方法

已知A＝（aij）3×3（aij＝aji）为三阶实对称矩阵，λ1（＝λ2）与λ3为A的两个互异的特征值，则求解正交矩阵Q，使得Q－1AQ＝Q′AQ＝diag（λ1，λ2，λ3）为对角矩阵的简便解法如下：

（1）对于A的二重特征值λ1（＝λ2），得到对应的齐次线性方程组（λ1E－A）X＝0的系数矩阵为λ1EA.易知λ1E－A的行向量成比例.取与λ1E－A的行向量共线的非零行向量记为ξ3′，那么列向量ξ3即为A的属于特征值λ3的一个特征向量；

（2）任取非零列向量ξ1，使得ξ1⊥ξ3，令与ξ3×ξ1共线的非零列向量为ξ2，那么ξ1，ξ2即为A的属于二重特征值λ1（＝λ2）的两个正交的特征向量；

（3）注意到，上述ξ1，ξ2，ξ3已两两正交，只需单位化即可得到标准正交向量组ε1，ε2，ε3.将ε1，ε2，ε3按λ1，λ2，λ3对应的次序按列构造矩阵Q，那么Q即为所求的正交矩阵.

值得注意的是，其中ξ3几乎不用计算即可从矩阵λ1E－A中直接得到；构造的正交矩阵Q是不唯一的，它取决于特征向量ξ1，ξ2，ξ3的选取.取相对较简洁的ξ1，ξ2，ξ3，使得构造出来的正交矩阵Q更简单.特别是对应重根λ1（＝λ2）的特征向量ξ1，ξ2的选取具有很大的灵活性，这是因为与ξ3正交的任何两个互相正交的非零向量都可以取作ξ1，ξ2.

1.2 理论证明

要证明以上的简便方法是正确的，即证ξ1，ξ2，ξ3是对应特征值的两两正交的特征向量.下面从两个方面证明：

（1）ξ1，ξ2是对应二重特征值λ1（＝λ2）的两个正交的特征向量；

（2）ξ3是λ3对应的特征向量.

证明 由于实对称矩阵一定可以对角化，因此特征值的几何重数等于代数重数.于是，又，所以r（λ1E－A）＝1，即λ1E－A的各行成比例.从而存在实可逆矩阵P，使得P（λ1E－A）＝C（C＝（ξ3，0，0）′；ξ3′为C唯一的非零行向量），即λ1E－A＝P－1C.

已知ξ1⊥ξ3，由叉积的性质，ξ2⊥ξ3，故有：

又ξ1⊥ξ2，所以ξ1，ξ2为属于二重特征值λ1（＝λ2）的互相正交的特征向量.

设η是A的属于特征值λ3的特征向量.根据实对称矩阵属于不同特征值的特征向量互相正交的几何特征，因为A为三阶实对称矩阵，且λ1≠λ3，所以ξ1⊥η，ξ2⊥η.又ξ1⊥ξ3，ξ2⊥ξ3，且ξ3，η均为非零向量，因而ξ3∥η，即ξ3也为A的属于特征值λ3的一个特征向量.

2 正交对角化方法的应用

2.1 三阶实对称矩阵的正交对角化

解 计算可得：

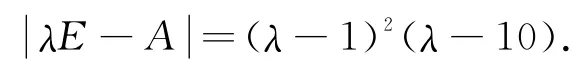
所以A的特征值为：λ1＝λ2＝1；λ3＝10.

由

取与非零行共线的向量（1，2，－2）记为，其转置ξ3＝（1，2，－2）′即为A的属于特征值λ3＝10的一个特征向量.再任取非零列向量ξ1，使得ξ1⊥ξ3，如ξ1＝（－2，1，0）′.令非零列向量ξ2∥ξ3×ξ1，如ξ2＝（2，4，5）′，则ξ1，ξ2即为A的属于二重特征值λ1（＝λ2）＝1的两个正交的特征向量.将ξ1，ξ2，ξ3单位化后按λ1，λ2，λ3对应的次序按列构造矩阵T，则即为所求正交矩阵，使得T－1AT＝T′AT＝diag（1，1，10）.

注 上例中ξ3是直接写出来的，并不需要经过复杂的计算；ξ1的选取不唯一，如还可以取ξ1＝（2，1，2）′，那么相应的ξ2可取ξ2＝（2，－2，－1）′.由此得到的正交矩阵为：

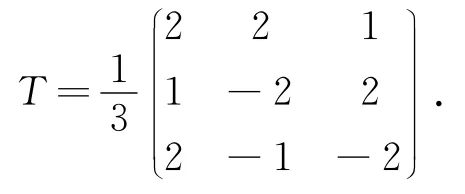
与常规方法相比，上述方法显然简洁很多，大大减少了计算量.

2.2 利用正交变换化二次型为标准形

三阶实对称矩阵有一个二重特征值的情形在考研题中是较复杂、常见的题型［8～9］，形式也可以有所变化.如下面的题型，本质上与上面的题型是相同的.

例2 利用正交变换将二次型f（x1，x2，x3）＝2x1x2＋2x1x3＋2x2x3化为标准形，并写出相应的正交变换和标准形.

解 此二次型矩阵为：

计算可得：

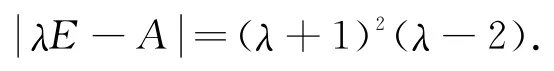
所以A的特征值为：λ1＝λ2＝－1；λ3＝2.

由

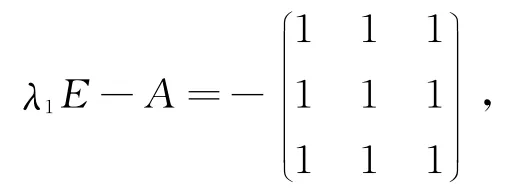
取ξ3＝（1，1，1）′，再取ξ1＝（1，－1，0）′（ξ1⊥ξ3）.由ξ2∥ξ3×ξ1得ξ2＝（1，1，－2）′，则ξ1，ξ2，ξ3即为A的对应λ1，λ2，λ3互相正交的特征向量.将ξ1，ξ2，ξ3单位化后构造正交矩阵，即为正交变换的矩阵，从而利用正交变换

将该实二次型化为标准形：

2.3 二次曲面方程的化简

例3［10］用正交变换化简二次曲面方程.

解 方程左端二次型的矩阵A的特征值为：λ1＝λ2＝5；λ3＝－4.

由λ1E－A易得正交矩阵

作正交变换x＝Cy，则二次曲面方程化简为：

显然，此处正交矩阵的选取较常规方法更为简洁，也更为快捷.

3 结论

本文给出一种简便方法，利用三阶实对称矩阵的二重特征值直接计算出三个彼此正交的特征向量，由此构造正交矩阵，从而有效地解决了此类矩阵有二重特征值时的正交对角化问题.一方面未涉及到利用矩阵的初等变换求齐次线性方程组基础解系的复杂过程，又避免了利用Schmidt正交化方法将二重特征值对应的特征向量正交化，大大缩小了计算量；另一方面正交矩阵的构造具有很大的灵活性，可通过构造简洁的特征向量得到较简单的正交矩阵.这种简便方法计算量小、可操作性强，在很大程度上可提高解题效率，降低错误率，达到事半功倍的效果.这类题型在高等数学和数学专业高等代数的考研卷中尤为常见，一般计算量都非常大，因此这种方法的引进对于解决相应问题具有重要意义.另外，这种方法还可广泛应用到利用正交变换化实二次型为标准形及化简二次曲面方程等题型中.因此这对于解决高等代数、解析几何等某些问题具有很高的实用价值.

［1］刘连福.由解方程组法求实对称矩阵的正交特征向量［J］.辽宁师专学报，2007，9（3）：105－106.

［2］金启胜.基于实对称矩阵标准型的变换研究［J］.甘肃联合大学学报，2012，26（6）：30－32.

［3］蔡静.实对称矩阵对角化的一种直接算法［J］.湖州师范学院学报，2007，29（2）：123－125.

［4］黄泽霞，胡劲松，郑克龙.求实对称矩阵的特征向量的一个简便方法［J］.成都工业学院学报，2014，17（4）：6－8.

［5］李蕊.实对称矩阵正交相似对角化的简便方法［J］.科技信息，2013（26）：139.

［6］顾央青.介绍求实对称矩阵正交特征向量的一种解题方法［J］.浙江工商职业技术学院学报，2003，2（3）：70－71.

［7］李先明.用行初等变换化实对称矩阵为对角形［J］.吉首大学学报，2001，22（4）：89－90.

［8］钱吉林.高等代数题解精粹［M］.北京：中央民族大学出版社，2002.

［9］龚冬宝.数学考研典型题［M］.西安：西安交通大学出版社，2003.

［10］张志让，刘启宽.线性代数与空间解析几何［M］.北京：高等教育出版社，2009.