一种多阀值神经网络盲信道均衡技术在海上通信系统中的应用

谭春波

(青岛黄海学院，山东 青岛266427)

0 引 言

海上无线通信系统中，由于海面气候环境以及海水折射反射等，其通信信道色散特性变化较快，并且多经干扰较为严重。传统的信道估算及均衡技术是利用训练序列来对信道参数进行计算，其优点是信道系数计算精度较高，缺点是信号带宽占用较大，且对信道变换较快的通信场景适应性较差，不能很好地自适应海上无线通信系统复杂多变的气候环境变换。

盲信道均衡技术［1-2］是近年来无线通信研究的热点，其完全利用接收端信号的统计学特性对传输的信道进行估算，在算法复杂度上有一定的提升，但是能很好的适应海面复杂多变的环境及信道变化，同时能有效克服海面噪声及多经干扰，目前在海上无线通信系统中得到一定的应用。

神经网络是模仿人的大脑神经组织而发展起来的一种信息处理技术，能够很好地处理复杂的统计学数据及非线性数学模型。本文研究了现有的基于神经网络的盲信道均衡技术，在此基础上提出一种新的多阀值神经网络盲信道均衡算法，最后给出算法的仿真结果。

1 盲信道均衡及神经网络原理

1.1 盲信道均衡模型及原理

盲信道均衡技术主要利用接收信号的统计学特性对海上通信信道进行信道补偿［3］，用以消除多经干扰及码间干扰。

在无线通信基带系统中，信道冲击响应h(n)与滤波器、调制调解器及信号损耗构成了整个通信系统的传输效应，假设原始数据x(n)为一幅值与时间都离散的离散信号，则接收端y(n)公式如下:

式中:h(n)为信道的冲击响应系数;s(n)为高斯白噪声。

若在时刻kT+ s0对y(n)进行抽样，则:

式中:xk(n0)h(n0)为没有任何干扰的接收信号;为无线通信中典型的码间干扰，在海上无线通信系统中，由于信道的突变较陆地严重，其码间干扰与海上噪声的叠加效应更加明显，最严重的时候有可能大于原始信号幅度。所以，盲信道均衡的本质即尽量消除这个干扰，从而最大幅度减少接收信号误码率。

盲信道均衡器原理如图1所示。

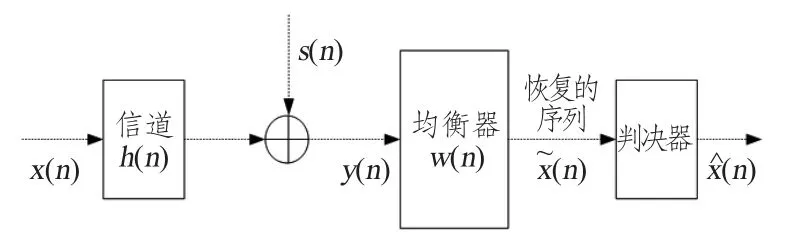
图1 盲信道均衡原理结构图Fig.1 The architecture diagram of blind channel equalization

1.2 神经网络模型及特征

神经网络算法是利用大量的相互关联的信号处理单元来模拟人脑的细胞处理结构，对数据进行智能化处理的一种技术。

神经网络模型结构［4］如图2所示。

图2 神经网元结构Fig.2 The schematic diagram of neural network

图2 中，输出表达式如下:

式中:ωij为神经网络系统中2个处理单元i 与j 之间的权值系数;xj为第j个处理单元的输入信息;θi为处理单元i的判断阀值;f(·)为输出信号的判断函数。

现有的神经网络模型有前馈神经网络及反向BP神经网络，本文在研究现有神经网络模型的基础上，设计一种3 层多阀值神经网络盲均衡算法。

2 多阀值神经网络盲信道均衡算法

2.1 基于神经网路的盲信道均衡器原理

其原理是将模拟神经网元作为整个信道均算法的控制器部分，用来对系信道参数进行自反馈控制，可以通过对迭代步长及神经网元之间的权值系数来改变整个算法的收敛速度及算法复杂度，达到实效性与结果精度之间的平衡。其原理如图3所示。

图3 基于神经网络控制器的盲信道均衡原理Fig.3 The architecture diagram of blind channel equalization based on neural network

在现有的盲信道均衡算法中，对于盲信道均衡器抽头系数最常用的算法是横模算法［5］，其迭代过程如下式所示:

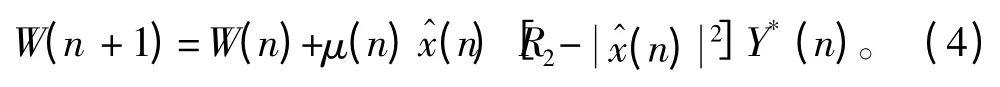
式中μ(n)为控制器步长因子，可以进行收敛速度的控制。

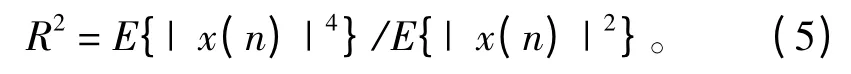
式(3)给出了神经网元的输出输入表达式，其中f(·)为阀值判断函数，表示整个神经网络的转换关系，所以基于阀值判断的神经网络最核心的即选择合适的f(·)。本文研究主要针对前馈神经网络，f(·)选择为f(x)=x+asinπx(a > 0，-∞< x < ∞)的sigmod 函数，因为该函数具有良好的平滑单调收敛性，有利于判决执行。

其f(x)的一阶导数为:

为了保证f(x)的单调特性，要求f′(x)=1+aπcosπx > 0。

式(6)中，还需要对a 进行选择，原则是幅值变化较大的信号，a 较大;幅值变化较小的信号，a较小。对于海上无线通信号，一般取a=0.38，以便更好地对接收信号进行判决。

2.2 多阀值神经网络均衡算法

多阀值神经网络严格说是一个非线性的网络系统，但是其能够对任意连续函数进行模拟，其网络结构如图4所示。

图4 多阀值神经网络控制器Fig.4 The schematic diagram of multi threshold neural network blind channel equalization

根据横模算法及前馈神经网元的处理机制，图4 中第2 层网元J 为代价函数，定义如下:

结合梯度最优的收敛法则，最终得到多阀值神经网络的各信号处理单元之间的权值系数公式:

式中η 为递推步长。

中间层J 与均衡器P 之间的权值系数迭代算法如下:

假设中间层J 与均衡器P 之间权值修正量有如下表达式:

当阀值判断函数f(x)函数为:

可以推导出其一阶导数函数为:

由式(10)～式(12)可以推导出中间层J 任意网元至均衡器输出层的权值系数迭代算式:

而输出层中间层之间的权值系数迭代算式为:

3 算法仿真

对多阀值神经网络盲信道均衡采用8 PAM 作为输入信号进行性能模拟，海面噪声为均匀的高斯白噪声，信噪比为20 dB，多经信道数为2。信道冲击响应函数如下:

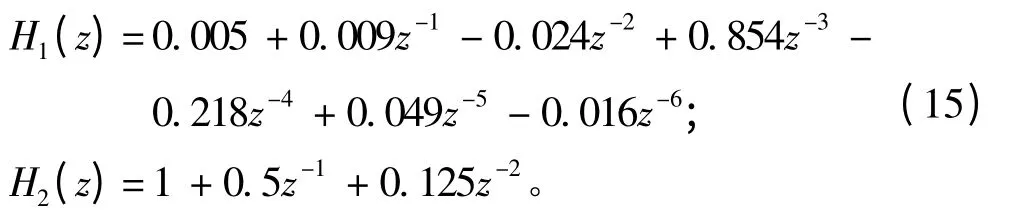
根据海面无线信道的实际情况，迭代补偿设置为η1=η2=η3=0.025。

各层之间的权值系数初始化为:

1)输入层至中间层的权值系数为:

2)中间层至输出层的权值系数为:

最后给出多阀值神经网络盲信道均衡算法和普通神经网络算法的误码率对比，如图5所示。

图5 误码率仿真图Fig.5 The map of BER simulation result

4 结 语

在海上无线通信领域，由于信道受到海面复杂多变的环境影响，信道的色散特性变化较快。传统的信道估算及均衡是利用训练序列进行计算，增加了信道的消耗，并且不利于复杂多变的海上无线信道。盲信道均衡技术利用接收端信号的统计学特性对传输的信道进行估算，能很好的适应海上无线通信环境。

本文研究了现有的基于神经网络的盲信道均衡技术，在此基础上提出了一种新的多阀值神经网络盲信道均衡算法，最后给出了算法的仿真结果。

［1］LIANG Qi-lian，ZHOU Zheng，LIU Ze-min.A new approach to global minimum and its applications in blind equalization［C］//IEEE International Conference on Neural Networks，1996:2113-2117.

［2］DESTRO FIHO J B，FAVIER G，TRAVASSOS ROMANO J M.Neural networks for blind equalization［C］//IEEE Trans.On Neural Networks，1996，21:196-200.

［3］ABRAR S.Slope and learning rate adaptation scheme for neural networks and its application to blind equalization［C］//IEEE Trans.on Signal Processing，2004，12(3):313-316.

［4］陶荣，詹锋.基于神经网络的海面噪声预测算法［J］.舰船科学技术，2015，37(2):172-175.TAO Rong，ZHAN Feng.Research on the ocean ambient noise prediction based on neural net［J］.Ship Science and Technology，2015，37(2):172-175.

［5］张瑜，贺秋瑞.基于混合系统的微弱信号参数提取方法［J］.舰船科学技术，2013，35(12):13-16.ZHANG Yu，HE Qiu-rui.The method of weak signal parameters extraction based on hybrid system［J］.Ship Science and Technology，2013，35(12):13-16.