自适应模糊滑模变结构制导律研究

杨益兴

(海军驻中国船舶重工集团公司第七〇一研究所军事代表室，湖北 武汉430064)

0 引 言

当导弹攻击固定目标时，比例导引律是一种设计简单、工程上易于实现、十分有效的导引律。但对攻击机动目标而言，比例导引律在理论上就存在很大的缺陷，它不能保证视线稳定，导致脱靶量很大［1-2］。以目标与导弹之间的相对距离、相对速度和目标加速度等信息为状态变量所产生的线性二次型最优导引律，虽然在理论上可以实现零脱靶量，但这种导引律形式过于复杂，需要信息太多，而且对信息误差敏感。较大的信息测量或估计误差会使其性能反而低于比例导引律［3］。逆系统控制方法、微分几何控制方法也为设计导引律提供了新的理论工具，但所设计出来的导引律也都由于形式复杂、需要信息多、鲁棒性差等缺点难以应用［4］。近些年来，研究对相对距离、相对速度和目标加速度测量或估计误差具有鲁棒性的导引律受到了人们的关注［5-6］。滑模变结构控制系统具有良好的抗干扰和抗参数摄动特性。因此，应用滑模变结构控制理论设计导引律是一条解决问题的途径［7-8］。但是，滑模变结构导引律中存在开关函数项，要求控制量进行切换。而在实际控制系统中，由于存在一定的时间滞后，控制量的切换不可能瞬时完成，或者系统建模存在位置部分，这些因素都会造成控制产生抖动［9］。这种抖动最终会表现为导弹弹体的抖动，如果抖动的幅度过大，不利于导弹部件的正常工作。因此，有必要研究变结构导引律的抖动问题。基于平行制导的控制方法，采用自适应模糊制导律，使用自适应模糊控制器来逼近变结构控制中的开关函数，使达到消除抖振的目的。而且提出的方法需要的信息量少，更易于工程实现。

1 导弹末制导数学模型

将导弹M和目标T 视为质点，在纵向平面内二维平面相对运动关系如图1所示。

图1 导弹和目标的相对关系运动图Fig.1 The relation of missile and target

由图1 可以得到导弹目标的相对运动方程

根据文献［4］，由式(1)～式(4)即可推出

其中uq和wq分别为导弹加速度和目标加速度在目标实现垂直方向上的分量，具体方程如下:

令x1为q，x2为，uq为控制输入，简化的系统如下

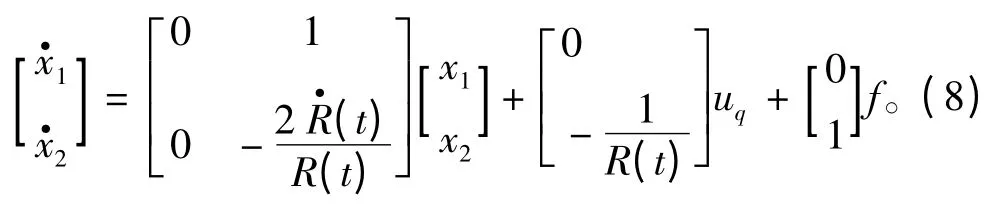
2 模糊自适应滑模制导律

2.1 传统的自适应滑模变结构制导律

制导方法选择平行接近法。即在整个引导过程中，目标线在空间保持平行移动的一种引导方法，即使(t)保持为0。

为了使系统状态方程(8)对参数摄动和干扰具有鲁棒性，考虑用变结构控制理论设计制导律。根据准平行接近原理，希望˙q(t)在制导过程中趋于0。因此，选取滑动模态为

使用趋近律的控制方法

式(10)表明随着拦截导弹与目标的不断接近，自动对趋近于滑模面的速度进行调整，尤其是当R 接近0 时，可以避免视线角速度的发散，在一定程度上也可以缓解抖振，k和ε 为正常数。

结合式(9)和式(10)，可以得到控制量为

由于在实际应用中，f 是目标的加速度，无法测量出，因此易实现的SMC控制的精确表达式为

其中ε > fmax。

根据Lyapunov 函数第二法，取一个Lyapunov 函数V=/2 ，可得

故只要满足k >1，ε > fmax，就可以得到<0。

2.2 模糊自适应滑模制导律

由上文推论可知，要实现Lyapunov >0，要求ε> fmax，由此来实现系统的鲁棒性，但这样同样也为控制系统带来了较大的抖振，不利于系统的实现。而模糊自适应系统具有万能逼近的作用［10］，故采用此方法构造来逼近εsgnx2，以达到削弱抖振，并估计误差，能够实现良好的效果。

采用模糊推理机、单值模糊器和中心平均解模糊器设计模糊系统，模糊系统的输出为，代入(8)，则控制律变为

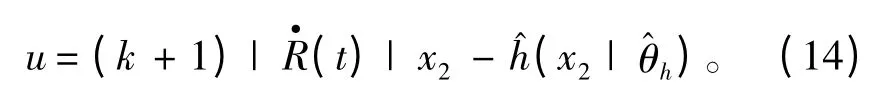
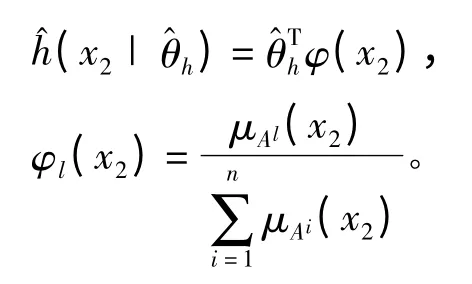
其中ε > fmax。

定义最优参数为

则可知:

其中，Ωh为的集合。

先对x2求导，得到

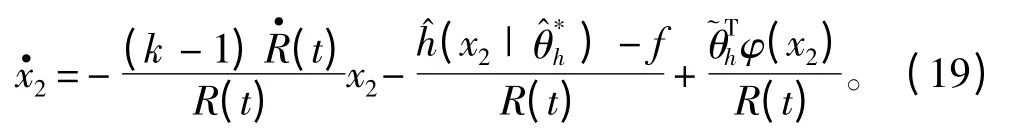
取Lyapunov 函数为

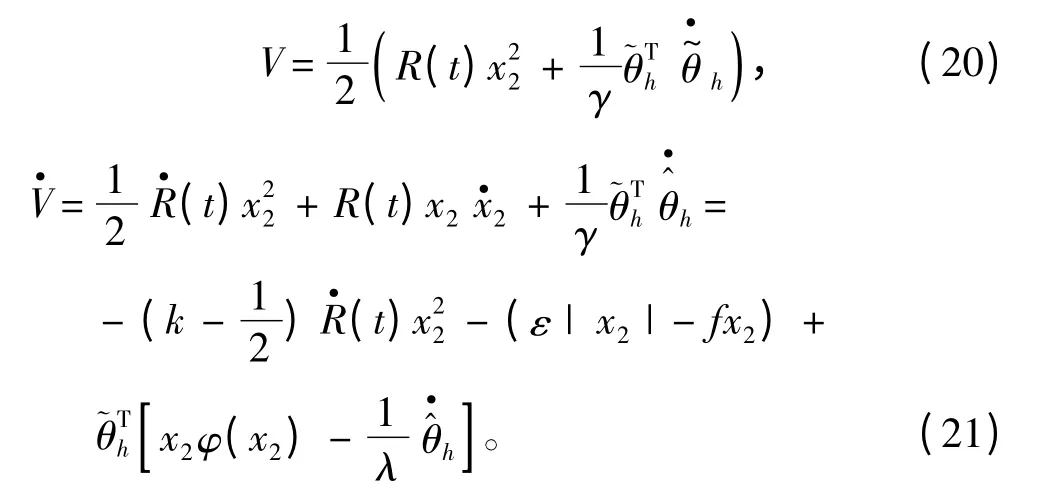
由ε > fmax，k > 1，，证得< 0。

3 仿真研究

选择Matlab的Simulink 模块对模糊自适应滑模制导律进行仿真，并与比例导引法、自适应变结构制导律的仿真结果进行对比。

首先选择模糊自适应部分隶属函数

模糊自适应滑模制导律中根据被控对象的知识给出规则，可以用来确定的初始值。模糊规则的选择并不是固定不变的，也可以使用其他初始值，然后由模糊自适应律进行自适应调整。本文中将的各个值的初始参数设置为10，λ 设为100。

设计的自适应滑模制导律与如下形式的比例导引和典型自适应滑模制导律进行性能比较，控制律分别为

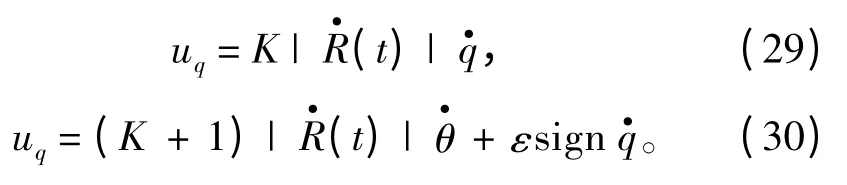
假设拦截导弹和目标的初始位置分别为(xM=0，yM=0 )和(xT=4 000，yT=5 000 )，拦截导弹的初始速度为800 m/s，视线角为q=53°，导弹速度方向φm=0° ，目标水平方向速度VTx=300 ，垂直方向速度初始时刻VTy=0 ，垂直方向上加速度aTy=50sin(0.5πt)。|(t)||(t)| 设为800。设导引头的测量盲区为150 m，进入盲区后停止对导弹的控制，导弹将保持现有的飞行速度和飞行方向。

仿真后得到视线角和视线角速率随时间变化的情况，以及各种制导下的脱靶量。

图2 视线角变化Fig.2 Varying law of line of sight angular

图3 视线角速率变化Fig.3 Varying law of line of sight angular rate

表1 脱靶量总结Tab.1 Summary of missile distance

从图2和图3 中可看出，在目标机动时，模糊自适应滑模制导在控制过程中实现了在目标加速度信息未知情况下视线角迅速收敛，视线角速率也迅速的收敛为0。而另外2 种制导方式却不能达到如此效果。对比比例制导和经典滑模制导，所研究的制导律具有更好的控制效果。

表1 中给出了在仿真中应用不同制导律情况下对应的脱靶量情况。可以看出，在脱靶量方面，自适应模糊滑模制导律具有明显优势。

4 结 语

基于导弹制导控制，本文提出了解决普通滑模抖振问题的自适应模糊滑模制导律，通过Lyapunov定理证明了控制律的稳定性，并通过仿真与比例制导、滑模制导相对比，体现了提出方法的优越性，证明了自适应模糊滑模制导律的有效性。

［1］周狄.寻的导弹新型导引规律［M］.北京:国防工业出版社，2002.

［2］吴进华，童红俊，李晓东.攻击大机动目标的L_2RG 研究［J］.海军航空工程学院学报，2006，21(05):501-505.WU Jin-hua，TONG Hong-jun，LI Xiao-dong.Research on L_2RG law against big maneuvering target［J］.Journal of Naval Aeronutical Engineering Institude，2006，21(05):501-505.

［3］王志清，李小兵，卓启明.智能滑模变结构制导律［J］.中国航天，2011(1):32-36.WANG Zhi-qing，LI Xiao-bing，ZHUO Qi-ming.Research on intelligent sliding-mode variable structure guidance law［J］.Aerospace Shanghai，2011(1):32-36.

［4］宋愿赟，陈万春.高精度快速趋近滑模变结构末端导引方法［J］.北京航空航天大学学报，2012，38(3):319-323.SONG Yuan-yun，CHEN Wan-chun.High-accuracy quickreaching sliding mode variable structure terminal guidance law［J］.Journal of Beijing University of Aeronautics and Astronautics，2012，38(3):319-323.

［5］周荻，慕春棣，徐文立.空间拦截智能自适应变结构导引规律研究［J］.宇航学报，1999，20(04):60-65.ZHOU Di，MU Chun-di，XU Wen-li.Intelligent adaptive variable structure guidance for space interception［J］.Journal of Astronautics，1999，20(04):60-65.

［6］LU Ping TSAO，Ching Show LIN.New optimal guidance law for short-range homing missiles［C］//Proc Natl Sci Counc Repub China Part Aphys Sci Eng，2000，24(6):422-426.

［7］BRIERLEY S，LONGCHAMP R.Application of sliding-mode control to air-air interception problem［J］.Aerospace and Electronic Systems，IEEE Transactions on，1990，26(2):306-325.

［8］ZHOU D，MU C，LING Q，XU W.Optimal sliding-mode guidance of a homing-missile［C］//Proceedings of the Decision and Control，1999 Proceedings of the 38th IEEE Conference on，F，1999:7-10.

［9］HSU L.Smooth sliding control of uncertain systems based on a prediction error［J］.International Journal of Robust and Nonlinear Control，1997，7(4):353-372.

［10］王立新.模糊系统与模糊控制教程［M］.北京:清华大学出版社，2003.