船舶主轴裂纹预测评估研究
盖力康,牟明磊,袁成清
(1.武汉理工大学 能源与动力工程学院可靠性工程研究所,湖北 武汉430063;2.武汉理工大学 船舶动力工程技术交通行业重点实验室,湖北 武汉430063)
0 引 言
船舶在我国的水路运输、海洋开发和海权捍卫中具有重要作用。船舶动力系统为船舶的正常航行、作业、战斗和其他需要提供推进动力和二次能源,被视为船舶的“心脏”。船舶轴系是船舶动力装置的重要组成部分之一。它的功用是将船舶主机发出的功率传递给螺旋桨,而螺旋桨的旋转所产生的轴向推船力,则通过轴系传递给推力轴承,再由推力轴承直接作用于船体上,迫使船前进和后退。
由于船舶航行环境的变化频繁,处于离岸、流动作业,船舶轴系持续运行时间长,工作条件恶劣,船舶轴系会在循环载荷或交变应力作用下产生裂纹和断裂,产生裂纹具有不可预见性,断裂具有灾难性和毁灭性。而目前我国船舶轴系安全保障现状是:依靠轮机员的经验为主;实行定期检修为主;执行事后服务为主[1]。为了改变现状,有必要将轴系运行保障方法、故障机理、检测手段和维修策略等进行深入的系统研究。通过对轴系裂纹的扩展机理和扩展趋势进行研究,探究其与船舶动力参数的关系,建立相应的可预测评估模型,寻求缓解裂纹故障恶化程度的环节和修复途径,提高船舶轴系运行的可靠性。
1 船舶主轴受力分析和Ansys 仿真
1.1 船舶主轴的应力分析
船舶主轴在弯扭复合疲劳载荷下运转,其上任意一点的应力状态可简化如图1所示,其中正应力σ 由弯矩来决定,切应力τ 由扭矩来决定。如果正应力与切应力同相位,且二者的比值随时间的变化为一常数,称为主轴比例加载疲劳,如图2(a)所示;如果正应力与切应力相位不同,这时正应力和切应力的比值随时间的变化不为常数,称为主轴非比例加载疲劳[2],如图2(b)所示。
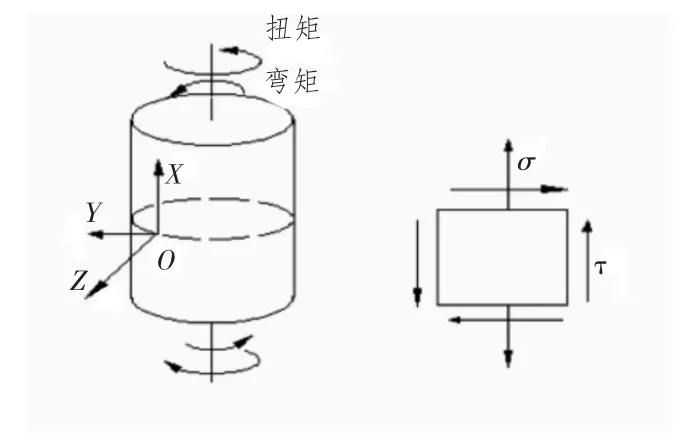
图1 主轴上任意一点的应力状态Fig.1 Stress state of any point on the spindle
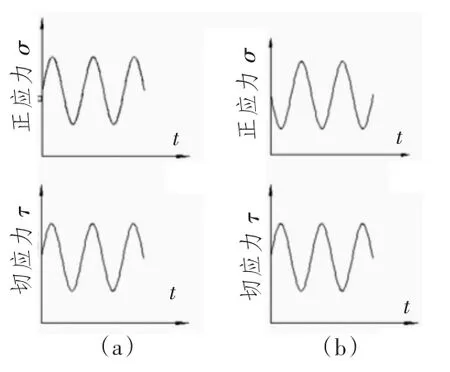
图2 比例载荷和非比例载荷Fig.2 The proportion of load and non-proportional loading
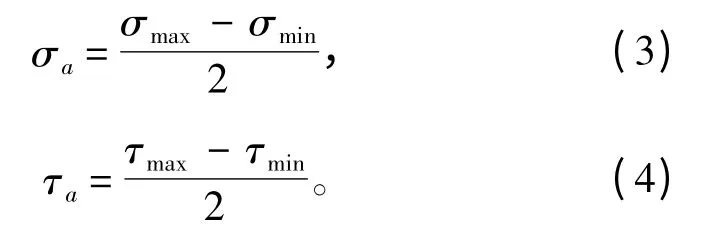
设任一与Z 轴平行,与X 轴成α 角的截面上的正应力与切应力为σa与τa,则

设σa为α 截面上正应力的幅值,τa为α 截面上切应力的幅值;σmax和σmin分别为一个载荷循环上的正应力的极大值和极小值;τmax和τmin分别为同一个载荷循环上切应力的最大值和最小值,则
1.2 主轴在不同扭矩下受力的Ansys 仿真
船舶主轴由推力轴、中间轴、尾轴3 部分组成,本文在Ansys 中把主轴简化为一根阶梯轴。主轴传递的功率其实也是传递扭矩,可以通过加载不同的扭矩来模拟船舶传送的不同功率。
具体建模如下:该阶梯轴由3 段不同直径和不同长度的圆柱组成:R1=0.2 m,L1=1 m,R2=0.3 m,L2=0.5 m,R3=0.25 m,L3=0.8 m,轴的弹性模量为2.12E10 Pa,泊松比为0.288。分别受1E3 N.m,1.5E3 N.m,2.5E3 N.m,4.0E3 N.m,2.0E3 N.m,0.5E3 N.m的扭矩。模型图如图3所示,网格划分如图4所示。
图3 主轴模型图Fig.3 Modeldiagram of shaft

图4 主轴网格划分图Fig.4 Meshing figure of the shaft
网格划分完成后施加不同扭矩得到阶梯轴的等效应力云图如图5~图9所示。

图5 1E3 N.m下主轴受力等效云图Fig.5 Stress equivalent figure under 1E3 N.m

图6 1.5E3 N.m下主轴受力等效云图Fig.6 Stress equivalent figure under 1.5E3 N.m

图7 2.5E3 N.m下主轴受力等效云图图Fig.7 Stress equivalent figure under 2.5E3 N.m

图8 2.0E3 N.m下主轴受力等效云图Fig.8 Stress equivalentfigure under 2.0E3 N.m

图9 0.5E3 N.m下主轴受力等效云图Fig.9 Stress equivalent cloud under 0.5E3 N.m
观察等效应力云图可以得到阶梯轴在不同扭矩下在相同位置出现了应力集中的部位,如图4 至图8所示的第3 段与第2 段轴的连接处,由弹塑性力学可知在应力集中时会出现裂纹。
2 断裂力学概述和用Ansys 计算应力强度因子
2.1 断裂力学概述
裂纹体根据外加作用力的不同,可分为Ⅰ型、Ⅱ型和Ⅲ型3 种基本断裂模式,如图10所示。Ⅰ型断裂也叫张开型断裂,受垂直于裂纹面的拉力;Ⅱ型和Ⅲ型断裂分别叫滑移型断裂和撕裂型断裂,它们都和剪切应力相关,Ⅱ型受平行于裂纹面并垂直于裂纹前缘的剪应力;Ⅲ型受平行于裂纹面并平行于裂纹前缘的剪应力[3]。

图10 三种断裂模型示意图Fig.10 Three kinds of fracture model
裂纹尖端的应力值和位移场以及能量释放率是典型的断裂力学参数,其中应力强度因子,能量释放率,J 积分被广泛应用于断裂力学中。本文着重介绍应力强度因子。
Irwin 根据弹性理论指出,在裂纹尖端附近的应力为[3]
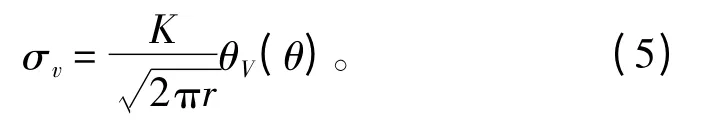
式中r和θ 为相对于裂纹尖端某一个点的极坐标;K为常数,它给定弹性应力场的大小,称为应力强度因子,其通式为[3]
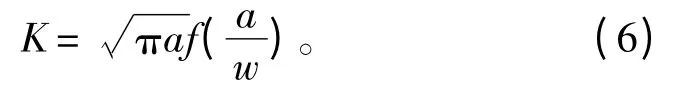
2.2 应力强度因子计算
Ansys 中提供一种基于相互作用积分法计算应力强度因子的计算方法。相互作用积分与J 积分的主区域积分法类似。它是不同于J 积分的一种积分方式,它比传统的位移扩展法精度高,需要的单元少。
相互作用积分的定义式为[4]:

式中:σki和σkj为真实场中的应力;uk,i为真实场中的位移;为辅助场中的应力;为辅助场中的位移;qi,j为裂纹扩展矢量;qn为裂纹扩展法向;δij为克罗尼茨符号。
相互作用积分与应力强度因子相关联的定义式为[4]
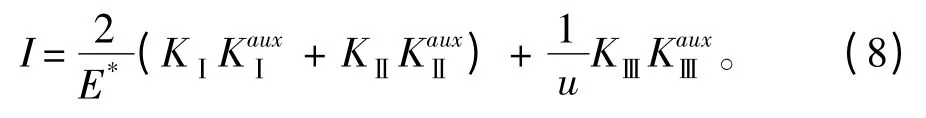
式中:Ki(i=1,2,3)分别为Ⅰ型、Ⅱ型和Ⅲ型应力强度因子;(i=1,2,3)分别为辅助场中的Ⅰ型、Ⅱ型和Ⅲ型应力强度因子;E*=E 为平面应力,E*=E/(1-V2)为平面应变(E 为材料的弹性模量;v 为泊松比;u 为剪切模量。
船舶主轴在不同扭矩下的应力集中处几乎在相同的地方,这样假设在应力集中的部位已经出现了裂纹。把不同扭矩下最大的等效应力提取出来,并根据相互作用积分法在Ansys 中计算经历一个时间载荷时的裂纹尖端的应力强度因子。以此来模拟主轴在不同功率下运转时动态的应力强度因子的变化。

图11 应力集中处裂纹模型图Fig.11 Crack model diagram in stress concentration
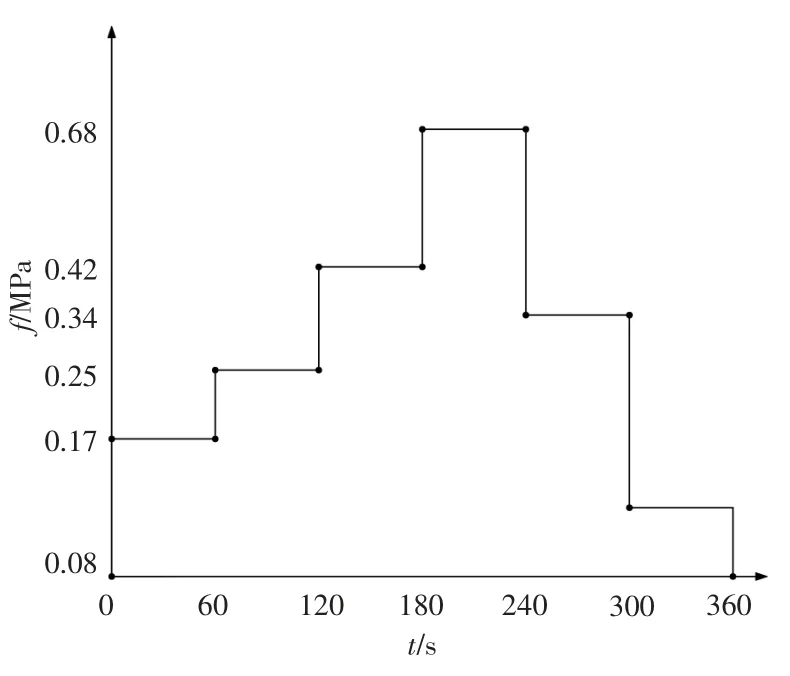
图12 载荷图Fig.12 Loading spectrum
模型简化为在半径为0.2 m的圆盘有一个长为0.02 m的裂纹(见图11),裂纹尖端处到圆盘边缘的一段直线上经历如图12所示的载荷下的应力强度因子的计算(其中的载荷是提取上文中不同扭矩下的最大应力)。
由于圆盘和裂纹都具有对称性,那么在Ansys可以建立如图13所示的模型。
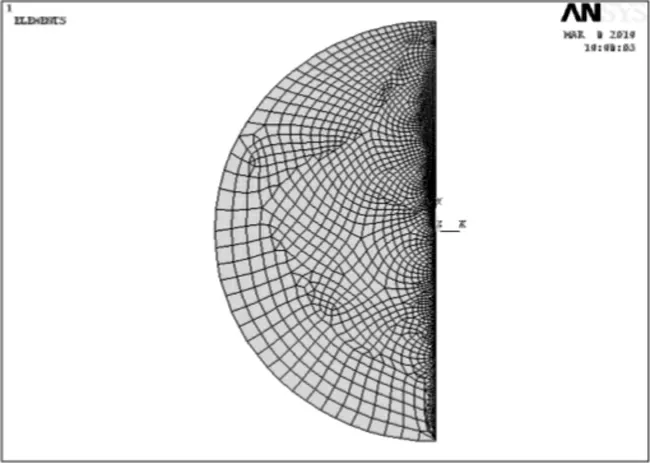
图13 计算应力强度因子的网格划分图Fig.13 Meshing diagram for calculation of stress intensity
经计算可得不同时刻圆盘的等效应力云图,现将裂纹尖端处放大可得如图14~图19所示。

图14 T=30 s 时裂纹尖端的等效应力图Fig.14 Stress equivalent figure of crack tip in 30 s
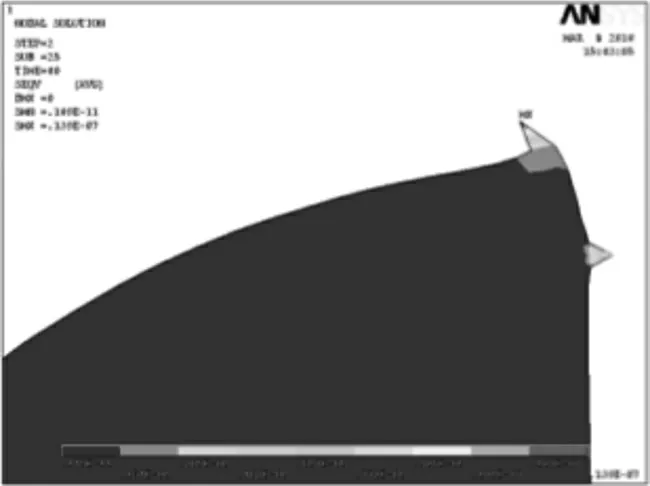
图15 T=90 s 时裂纹尖端的等效应力图Fig.15 Stress equivalent figure of crack tip in 90 s
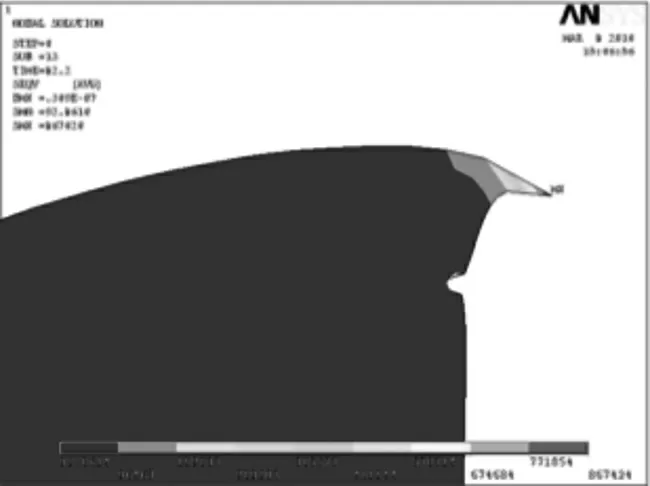
图16 T=150 s 时裂纹尖端的等效应力图Fig.16 Stress equivalent figure of crack tip in 150 s
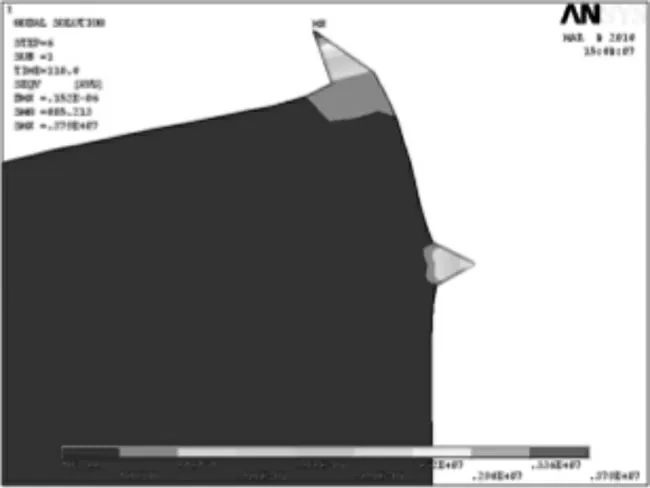
图17 T=210 s 时裂纹尖端的等效应力图Fig.17 Stress equivalent figure of crack tip in 210 s

图18 T=270 s 时裂纹尖端的等效应力图Fig.18 Stress equivalent figure of crack tip in 270 s
图19 T=330 s 时裂纹尖端的等效应力图Fig.19 Stress equivalent figure of crack tip in 330 s
可以得到裂纹尖端处等效应力随时间变化曲线图。

图20 裂纹尖端的等效应力值变化曲线Fig.20 The curve of stress equivalent on crack tip
将计算的KⅠ型和KⅡ型应力强度因子统计如图21和图22所示(这里所得KⅠ和KⅡ都经过优化处理)。即
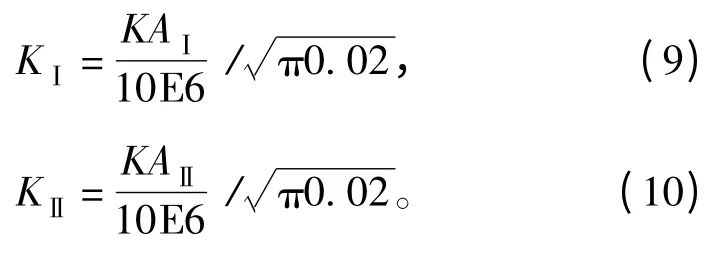
式中:KAⅠ和KAⅡ为真实的应力强度因子;0.02 为裂纹的长度。这样做的目的是为提高记录应力强度因子的精度[5]。
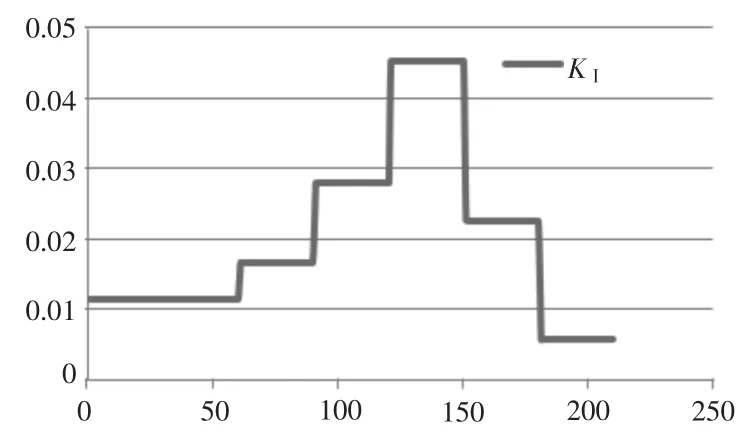
图21 KⅠ优化值随时间的变化曲线Fig.21 The curve of KⅠoptimal value along with the change of time
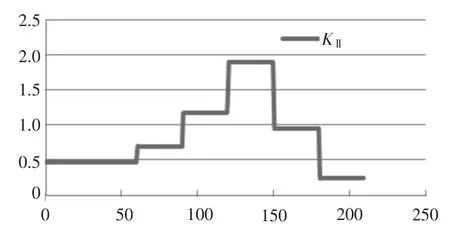
图22 KⅡ优化值随时间的变化曲线Fig.22 The curve of KⅡoptimal value along with the change of time
从图表可看出,应力强度因子随着作用力的增大而增大,即随着作用于轴的扭矩的增大而增大。
3 基于Paris 公式的主轴裂纹扩展速率的推导
船舶主轴的疲劳裂纹形成后,最令人担心的是裂纹扩展,以及由于裂纹扩展对轴系安全性的影响。
对于疲劳裂纹扩展速率的研究,主要在于寻求裂纹扩展速率与有关各种力学参数之间的数学表达式。如果在应力循环ΔN 次之后,裂纹扩展量为Δa,则应力每循环1 周,裂纹扩展Δa/ΔN 为“裂纹扩展速率”,在极限条件下,用微分da/dN 表示[6]。
对于裂纹扩展速率,近年来国内外做了大量的研究工作,取得了不少成绩。在单轴循环交变应力下,垂直于应力方向的裂纹扩展速率,一般可写成以下形式:

式中:N 为应力循环次数;σ 为正应力;a 为裂纹长度;c 为与材料有关的常数。
1961年,美国人Paris 提出了计算恒幅载荷下裂纹扩展寿命的Paris 公式[7]:
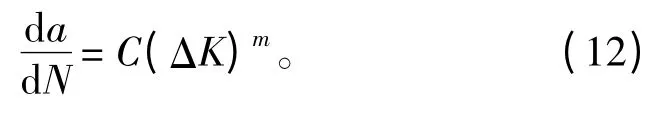
式中:ΔK 为应力强度因子范围,ΔK=Kmax- Kmin;C,m 为材料常数。此公式大体适用于各种材料亚临界裂纹扩展试验数据处理,且只适合描述Ⅱ区(中部区)裂纹扩展行为[7]。
对于船舶主轴的裂纹扩展问题,想找到裂纹扩展与船舶动力参数的关系。其动力参数包括船舶轴系的转速和船舶轴系传递的功率等。
假设主轴传递的功率为Pk,主轴的转速为n,那么由弹性力学可得作用在轴上的外力偶
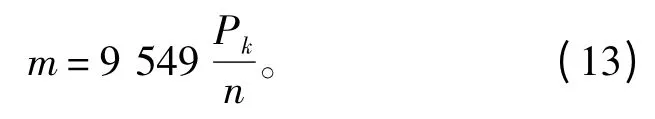
这个外力偶即为作用在主轴上的扭矩T。圆轴扭转时,平衡外力矩由横截面上无数的微剪力组成。如图23所示,设距圆心ρ 处的切应力为τp,经过微分理论推导可得横截面上任一点处的切应力为

式中:T 为横截面上的扭矩;ρ 为横截面上任一点到圆心的距离;IP为横截面对形心的极惯性矩。
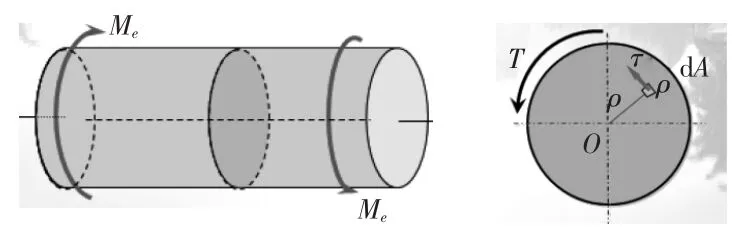
图23 纯扭矩作用下的轴的受力分析图Fig.23 The stress analysis diagram of the shaft under pure torque load
为进行理想化处理,假设船舶主轴只承受扭转力矩,那么在横截面的周边上切应力最大。
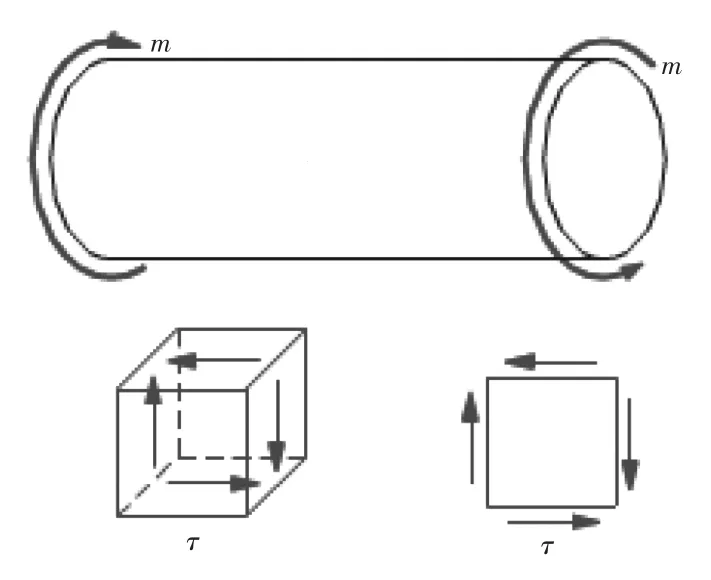
图24 纯扭矩下轴上任一点的受力分析图Fig.24 The stress analysis diagram of any point of the shaft under pure torque load
在这种条件下,σX=σY=0,从而得到

由上式可知,当a=-45°时,σa为极值且σa=0,代入可得

由Paris 裂纹扩展公式
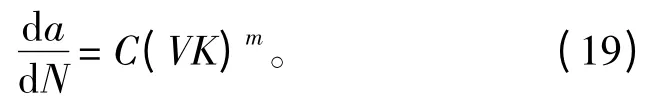
式中c和m 均为与材料有关的常数,对于钢铁类材料m的取值常在2~4 之间。其中应力强度因子幅度[3]:
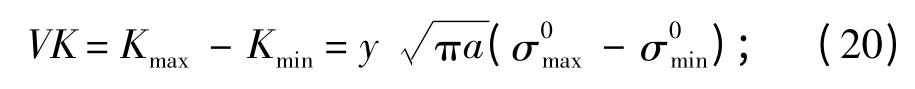
应力强度因子

式中:y 为表示裂口位置和几何形状的系数;σ0为外载荷的对裂口作用的名义应力;a 为裂口的长度。
综上分析可得:

由此可见,可以通过调整传递功率Pk和主轴转速n 来控制船舶主轴的裂纹扩展速度。
4 结 语
1)基于Paris 公式的推导,当船舶主轴出现裂纹时,可以相应地提高转速,降低输出功率,或者同时提高转速和降低输出功率,来控制主轴裂纹的扩展速度。
2)通过本文提到的关于找出船舶主轴在扭矩作用下的应力集中部位,计算出该处的应力强度因子,并与材料的临界断裂应力强度因子比较,可以预测和评估裂纹的产生与扩展。
3)得到调节转速与功率控制裂纹扩展的方法后,再结合裂纹预测技术,建立一个裂纹预测评估体系可行。这样的话当船舶主轴在裂纹萌生后,然后根据当前的转速和功率得到一个裂纹扩展速率曲线,在评估系统模拟改变主轴的转速和功率得到一个裂纹扩展速率最慢的转速和功率值,然后将模拟结果传达到船舶柴油机的控制系统。这样就可以建立一套控制裂纹扩展的自修复系统。
[1](苏)维列捷.船舶轴系的修理[M].叶鸣高,等译,北京:人民交通出版社,1958:16-19.
[2]王国军,胡仁喜,陈欣,等.N-Soft 疲劳分析理论与应用实例指导教程[M].北京:机械工业出版社,2007:152-156.
[3]李庆芬.断裂力学及其工程应用[M].哈尔滨:哈尔滨工程大学出版社,2007:4-6.
[4]王泓.材料疲劳裂纹扩展和断裂定量规律的研究[D].西安:西北工业大学,2002.
[5]张洪才.ANSYS14.0 理论分析与工程应用实例[M].北京:机械工业出版社,2013:468-470.
[6]JEN Yi-ming,YIP Ming-chuen,WEI Cheng-long,et al.Prediction of low-cycle contactfatigue life of sleeve-pin-shaft connections under axial and torsional cyclic loading[J].International Journalof Fatigue,2007(29):796-809.
[7]CITARELLA R,CRICRI G.Comparison of DBEM and FEM crack path predictions in a notched shaft undertorsion[J].Engineering Fracture Mechanics,2010(77):1730-1749.

