装甲车辆新型变速箱故障诊断研究
李 军,昝 宝
(装甲兵工程学院,北京 100072)
由于服役环境严酷、载荷复杂多变,在役装甲车辆变速箱行星齿轮系统故障率居高不下,一旦发生故障,维修成本非常高,而齿轮故障是齿轮箱故障的重要形式之一.齿面点蚀是装甲车辆变速箱行星齿轮传动系统早期故障形式之一,研究该故障对系统振动特性的影响,对于系统早期故障诊断和状态监测具有重要意义.
目前针对行星齿轮系统动力学研究主要集中在动力学建模和动态特性分析方面.Kahraman等[1]建立了考虑部件横向、纵向及扭转方向位移、齿轮时变刚度、齿侧间隙等的动力学模型;Parker等[2-3]在此基础上建立了考虑陀螺效应以及齿圈柔性的动力学模型,并应用到高速行星齿轮系统中.在含故障的系统动力学研究方面,目前一些学者开展了针对定轴齿轮系统的研究[4-6],但行星轮系统由于具有振动传递路径比较复杂,故障响应不明显;一般行星轮系统处于低速重载的运行环境,低频特征频率成分受噪声污染严重,使得故障特征频率分析困难等特征[7],使得针对定轴齿轮系统的一些常用建模方法及故障诊断技术无法解决行星齿轮系统故障诊断所面临的难题,所以开展行星齿轮故障系统动力学建模及故障诊断研究迫在眉睫.Chaari等[8-9]通过频域和能量分析方法研究了太阳轮轮齿出现点蚀和裂纹时系统的动态响应.但论文没有对太阳轮故障特征进行详细分析,也没有对行星轮故障、齿圈故障进行研究.Sharad等[10]研究了行星轮轴承内外圈故障对系统动态响应的影响.
综上所述,目前还很少有针对行星齿轮系统,深入研究点蚀对系统动态响应的影响,并分析其故障特征.因此,本研究将基于材料力学理论,给出含点蚀的轮齿啮合刚度定量描述方法;进而建立行星齿轮系统点蚀故障动力学模型;采用数值方法研究太阳轮、行星轮以及齿圈发生点蚀时对行星系统啮合刚度及动态响应的影响,着重探讨故障频率的特点以及不同点蚀宽度、深度和位置对部件频谱特性的影响,为行星齿轮系统的故障诊断及机理研究提供参考.
1 轮齿变形量的数值计算
1.1 正常齿轮啮合刚度
在计算齿轮啮合变形时,一般将轮齿看成变截面悬臂梁(如图1所示),轮齿的变形由弯曲变形、压缩变形、剪切变形、基圆柔体变形和接触变形组成[10].
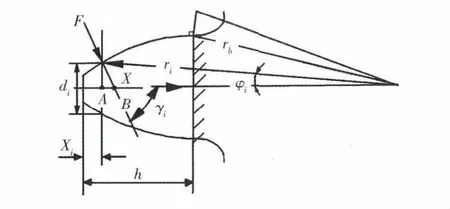
图1 单齿悬臂梁示意图[11]
其中弯曲变形、压缩变形及剪切变形公式见式(1)~式(3):
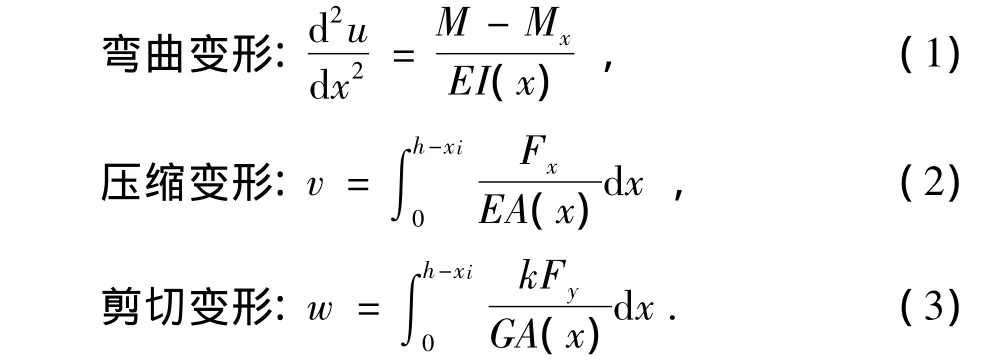
基圆柔体变形 δf可由 Weber[11]提出的公式进行计算,赫兹接触变形δC可由Yang和Su[11]的研究进行计算.
综上所述,在法向力F作用下,啮合线与齿轮中心线交点B(图1)的总变形量为:
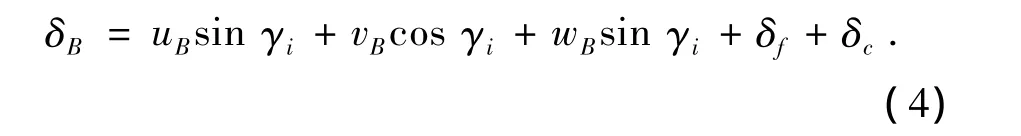
所以,轮齿任意位置i的刚度可表示为:
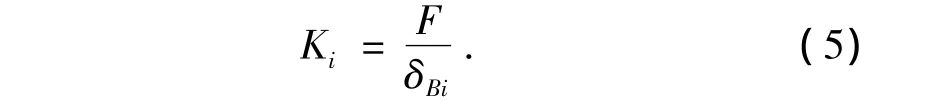
一对齿轮啮合时,可以看成是两个不同刚度的弹簧串联连接,其综合啮合刚度可表示为:
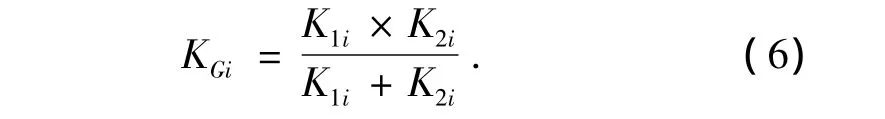
两对齿轮啮合时,可以看成是两个串联弹簧再并联连接.
1.2 齿轮点蚀时的啮合刚度
齿轮在长期工作后,齿面会发生接触疲劳破坏,导致表面点蚀,出现点状小坑,形成点蚀.研究表明,当齿面发生点蚀时,会影响齿轮对啮合时齿轮的变形量,使时变啮合刚度发生改变,从而对齿轮系统的动态响应产生影响.根据啮合变形计算公式可知,当齿面发生点蚀时,如图2所示,会改变单齿悬臂梁的横截面积,影响式(1)~式(3)中I(x)和A(x)的大小,从而影响弯曲变形、压缩变形及剪切变形的变形量.
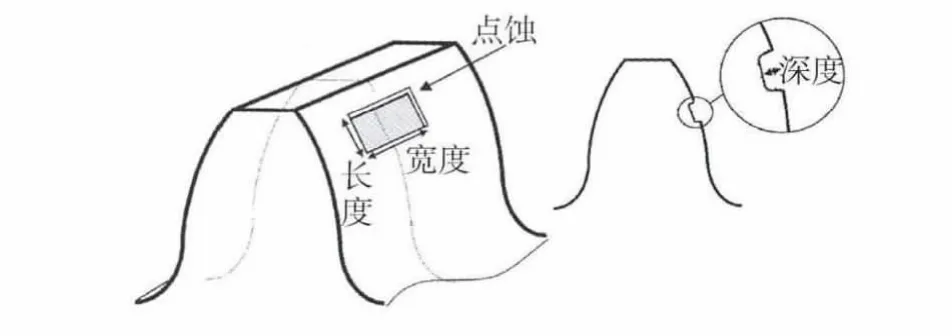
图2 齿面点蚀示意图[4]
2 行星齿轮动力学模型
搭建的行星齿轮系统模型为弯扭耦合的动力学模型,如图3所示,系统包括太阳轮(S),框架(C),齿圈(r),以及四个行星轮(P),轴承的支撑考虑为线性弹簧,齿轮啮合考虑为沿啮合线方向的线性弹簧,每个部件考虑横向(X)、纵向(Y)及扭转(U)方向的位移,模型中各部件变量参考坐标系随框架转动,其中太阳轮、齿圈、框架的坐标系原点与框架中心重合,行星轮参考坐标系原点为各自圆心,旋转方向均取逆时针方向为正[12].
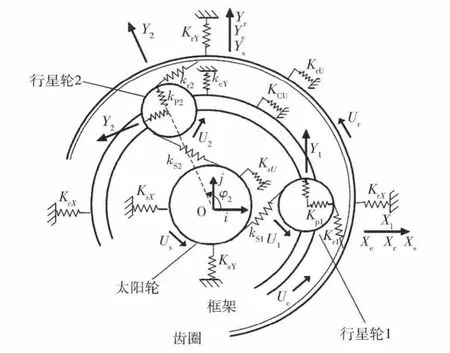
图3 行星系统动力学模型
系统动力学方程为:
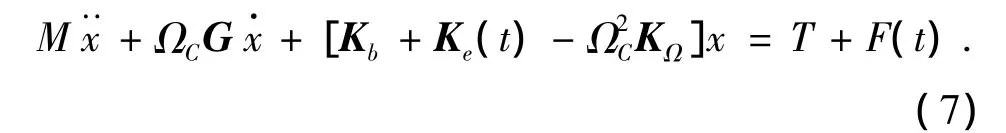
式中:Ωc为框架的角速度;T为外扭矩矩阵;F(t)为外激励力矩矩阵;M为质量矩阵,可以表示为:

G为陀螺矩阵,可以表示为:
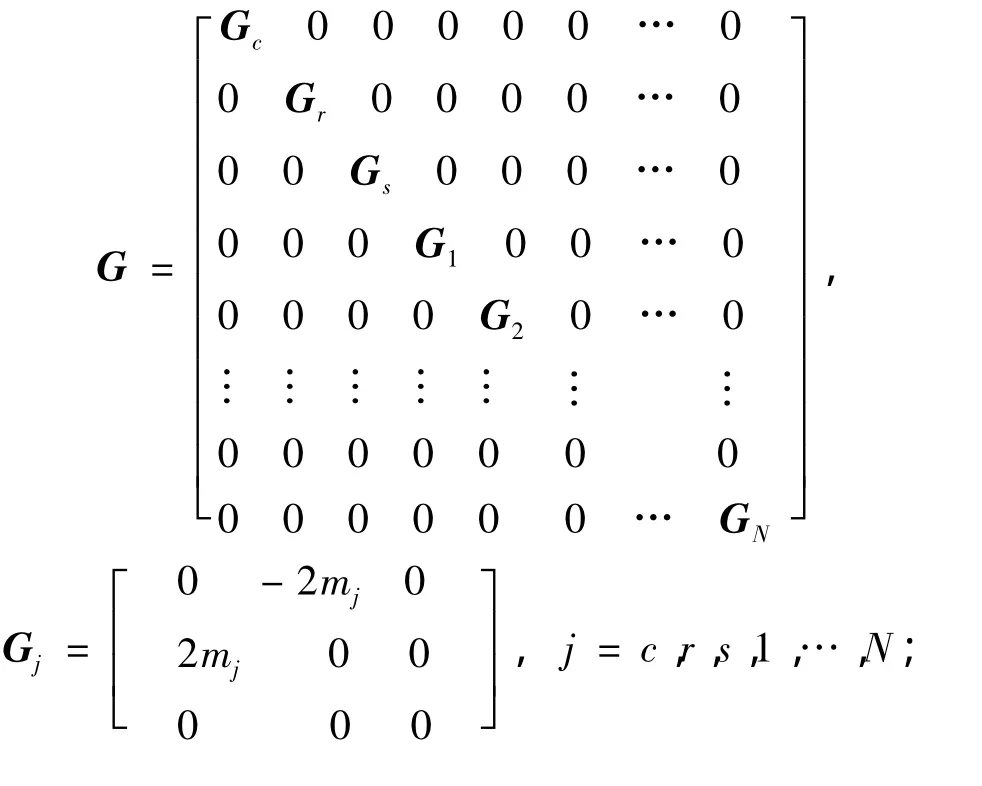
Kb为轴承的支撑刚度矩阵,可表示为:
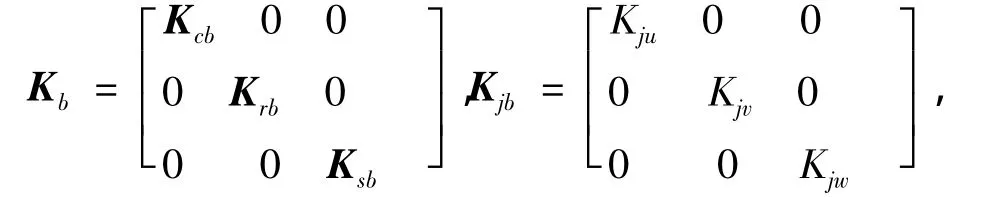
j=c,r,s,其余不足阶数为零;
KΩ为向心力矩阵,可表示为:
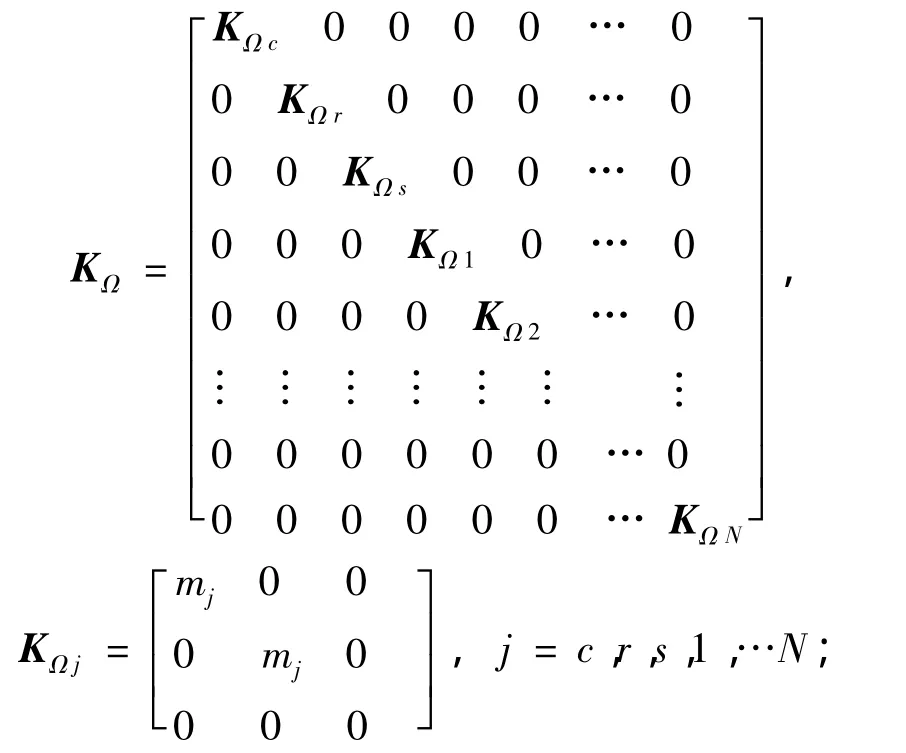
Ke(t)为啮合刚度矩阵,可表示为:

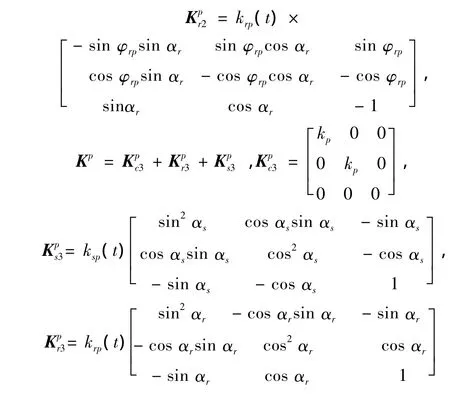
3 点蚀对啮合刚度的影响研究
采用数值解法,研究了点蚀对时变啮合刚度的影响,表1为行星齿轮系统参数.
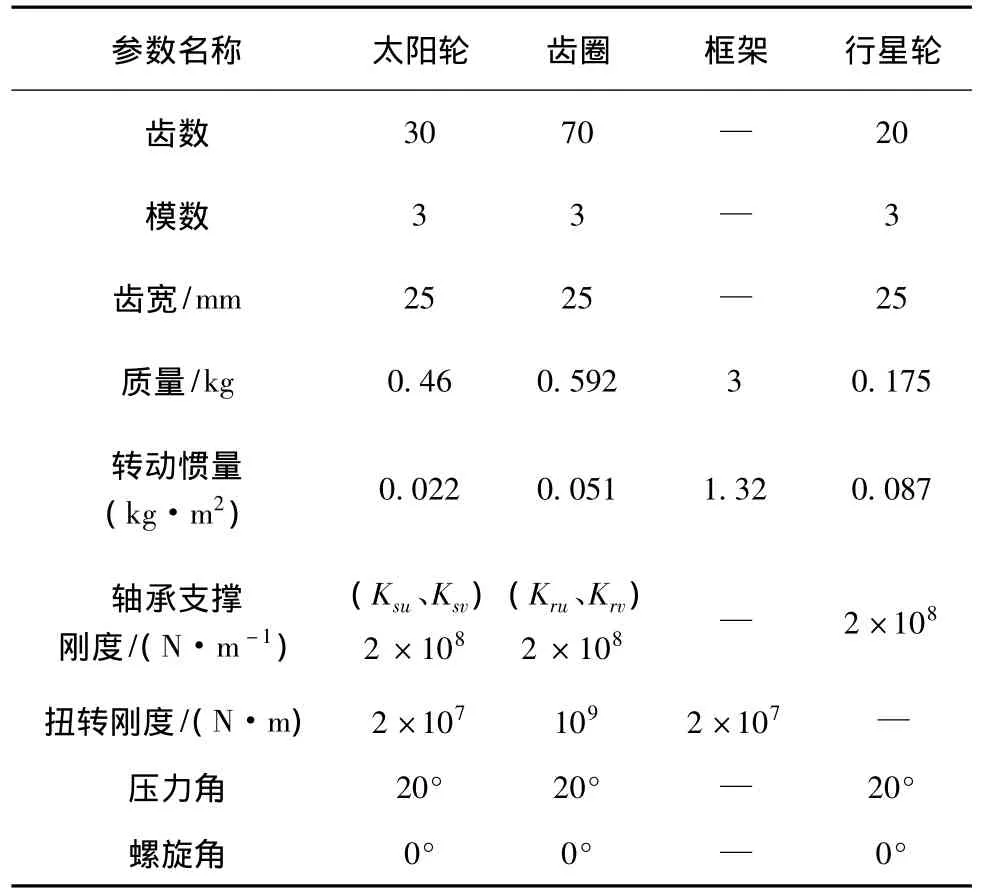
表1 行星齿轮系统参数
假设点蚀出现在太阳轮某齿齿面中部,深度1 mm,长度1.1 mm,点蚀宽度分别为10 mm、15 mm、20 mm.图4为点蚀对太阳轮与行星轮之间时变啮合刚度的影响图.从图中可以看出:不同点蚀宽度不影响时变啮合刚度在一个啮合周期内的变化起始时刻,但会影响时变啮合刚度变化量的大小,宽度越大,刚度的减小就越大.
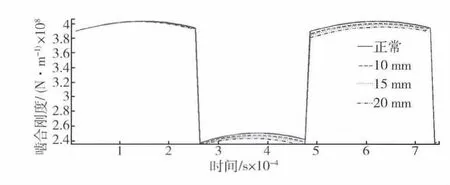
图4 不同点蚀宽度对时变刚度的影响
4 点蚀对齿轮系统的影响研究
4.1 齿轮正常状态下的系统响应
假设框架输入恒定扭矩1000 N·m,转速1800 r/min,齿圈固定.通过式(8)~式(10)计算得到框架旋转频率为30 Hz,太阳轮旋转频率为100 Hz,行星轮旋转频率为 75 Hz[13].
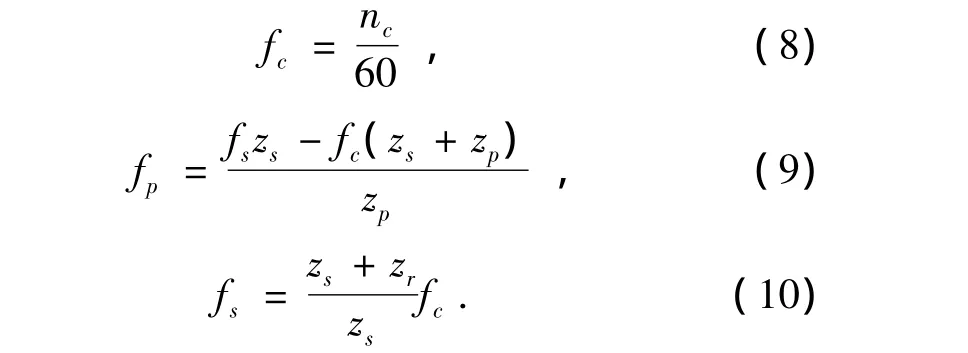
由式(11)计算得到啮合频率2100 Hz.

采用NEWMARK法对系统进行求解.图5为系统在正常状态下,太阳轮和行星轮1在扭转方向上振动的频谱图.从图中可以看出,部件的振动主要以啮合频率及其倍频振动为主.
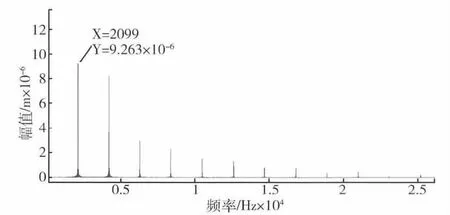
图5 正常状态下太阳轮扭转方向频谱图
4.2 齿面点蚀对行星齿轮系统振动特性的影响
若框架转速、扭矩不变,当太阳轮、行星轮以及齿圈出现点蚀且点蚀程度均为长1.1 mm、宽10 mm、深0.5 mm时,太阳轮扭转方向频谱图如图6~图8所示.图中出现了明显的边带,故障频率分别为 N(fs-fc)、N(fp+fc)以及 Nfc(N=1,2,… ).
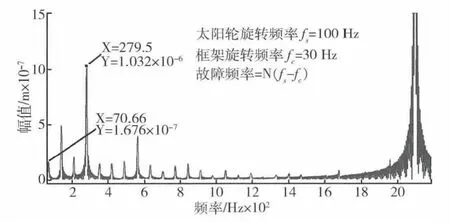
图6 太阳轮点蚀时太阳轮扭转方向频谱图

图7 行星轮点蚀时太阳轮扭转方向振动频谱图
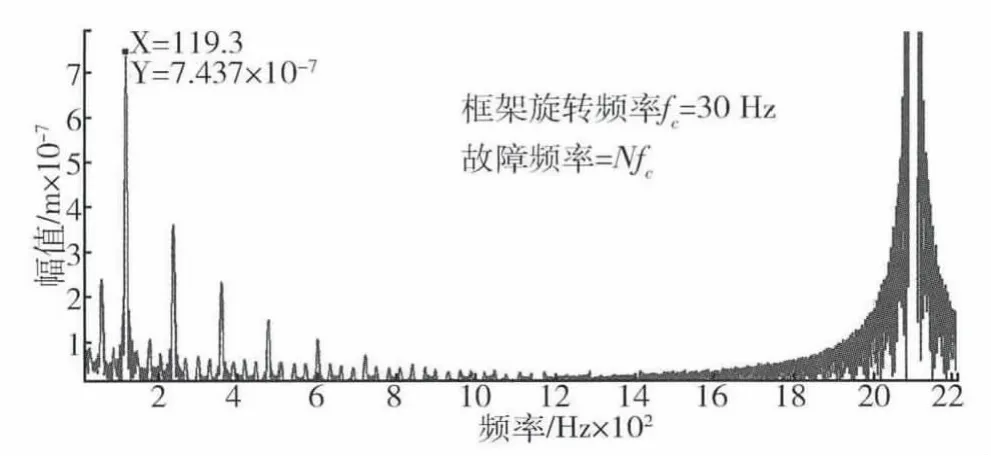
图8 齿圈点蚀时太阳轮扭转方向振动频谱图
5 结论
1)当发生齿面点蚀时,啮合刚度会降低,且随故障程度发生变化;
2)当太阳轮发生点蚀时,故障特征频率为太阳轮旋转频率与框架旋转频率差及其倍频,即N(fs-fc)(N=1,2,…).当行星轮出现点蚀时,各部件故障特征旋转频率为行星轮旋转频率与框架转频之和及其倍频,即N(fp+fc)(N=1,2,…).当齿圈出现点蚀时,故障频率为 Nfc(N=1,2,… ).
[1]Kahraman A.Natural modes of planetary gear trains[J].Journal of Sound and Vibration,1994,173(1):125-130.
[2]Wu.X,Parker.R.G,Modal properties of planetary gears with an elastic continuum ring gear[J].Journal of Applied Mechanics,2008,75,031014.
[3]Parker RG,Wu X.Vibration modes of planetary gears with unequally spaced planets and an elastic ring gear[J].Journal of Sound and Vibration,2010,329:2265-2275.
[4]Chaari F,Baccar W,Abbes M S,etal.Effect of spalling or tooth breakage on gearmesh stiffness and dynamic response of a one-stage spur gear transmission[J]. European Journal of Mechanics,2008,27:691-705.
[5]Chen Zai-gang,Shao Yi-min.Dynamic simulation of spur gear with tooth root crack propagating along tooth width and crack depth [J].Engineering Failure Analysis,2011,18:2149-2164.
[6]马 锐,陈予恕.含裂纹故障齿轮系统的非线性动力学研究 [J].机械工程学报,2011,47(21):84-90.
[7]雷亚国,何正嘉,林 京,等.行星齿轮箱故障诊断技术的研究进展 [J].机械工程学报,2011,47(10):60-66.
[8]ChaariF,Fakhfakh T,Haddar M. Analytical investigation on the effect of gear teeth faults on the dynamic response of a planetary gear[J].Noise &Vibration Worldwide,2006,9:9-15.
[9]Chaari F,Fakhfakh T,Haddar M.Dynamic Analysis of a Planetary Gear Failure Caused by Tooth Pitting and Cracking[J]. Journal of Failure Analysis and Prevention,2006,6(2):73-78.
[10]Jain S,Hunt H.Vibration Response of a Wind-turbine Planetary Gear set in the Presence of a Localized Planet Bearing Defect[C],IMECE2011-63452.
[11]孔德文.大型齿轮传动装置动力学及故障诊断技术研究[D].吉林:吉林大学,2008.
[12]Chaari F,Fakhfakh T,Hbaieb R,etal.Influence of manufacturing errors on the dynamic behavior of planetary gears[J].The International Journal of Advanced Manufacturing Technology,2006,27:738-746.
[13]赵镭镭.行星齿轮传动机构的故障诊断研究 [D].北京:北京科技大学,2011.

