运用灰色系统GM（1，1）模型预测安徽省肺结核发病趋势

宋红兵 洪光烈

安徽省庐江县疾病预防控制中心，安徽庐江 231500

运用灰色系统GM（1，1）模型预测安徽省肺结核发病趋势

宋红兵 洪光烈

安徽省庐江县疾病预防控制中心，安徽庐江 231500

目的 建立肺结核灰色预测模型GM（1，1），应用于安徽省肺结核发病趋势的预测。 方法 根据公共卫生科学数据中心中2005～2012年安徽省肺结核发病报告资料建立肺结核发病率灰色预测模型GM（1，1），同时采用该模型对安徽省2013～2015年的肺结核发病率进行预测分析。 结果 通过灰色预测模型GM（1，1）而建立一个Y（t）=-1433.7369e-0.0654（t-1）+1531.5997预测模型，利用建立的模型预测安徽省2013 ～2015 年安徽省肺结核发病率分别为57.4372/10 万、53.7996/10万和50.3923/10万。 结论 通过实践应用证实，GM(1，1)模型预测安徽省肺结核发病率符合目前发展趋势，结果具有较高的参考应用价值。

肺结核；GM（1，1） 模型；安徽省；预测

结核病是一种经空气传播的慢性传染病，1例传染源每年可以通过空气传染10～15名健康人。相关报道显示：我国已经成为全球结核病高发国家，到目前为止我国结核病发病人数已经达到130万人，表明我国面临严峻的结核病防控形势[1-2]。

本文根据我国著名学者邓聚龙教授创立的灰色系统理论，该理论主要是基于原始数据处理以及GM（1，1）模型，由此发现、掌握研究对象的发展规律性。在实际应用中，我们发现该模型会受到样本含量、概率分布等因素影响较小，因此可用于临床医学流行疾病的预测工作[3-5]。本文根据公共卫生科学数据中心2005～2012年安徽省肺结核病例报告资料，并通过灰色系统GM（1，1）模型预测安徽省肺结核发展趋势，旨在为安徽省制定合理的结核病防控措施提供数据支持。

1 资料与方法

1.1 资料来源

本文所涉及的肺结核年发病率数据均来自公共卫生科学数据中心中2005～2012年安徽省肺结核发病报告资料。

1.2 模型原理

在实际应用中，可利用灰色模型对采集的随机、离散原始数据进行n次累加，并最终形成一个具有一定规律性的累加生产数据，这样可以最大化减弱原始数据的波动性、随机性，从而增强数据的规律性、合理性；最后对生成的数据做一个序列建模，通过模型再次进行m次累减，以此来还原预测值。

1.3 模型拟合效果检验

为了能够验证GM（1，1）模型应用的准确性，可以采用后验差法对预测结果进行检验，利用后验差法所计算出来的后验差比值C、小误差概率P来综合评估模型的预测准确度。在实践操作中可参照如下判断标准评估模型的优劣性：若C＜0.35、P＞0.95时，模型预测值为优；C＜0.45且P＞0.80，模型判为良；C＜0.5且P＞0.70，模型判为中；C＜0.65，P＜0.70，模型判为差。

1.4 灰色系统GM（1，1）模型的建立步骤[6-7]

1.4.1 一次累加生成 我们可以设置预测原始数列：X（t）=|x（1），x（2），…，x（n）|，通过模型对原始数列进行一次累加生成，这样可以有效强化数列的规律性，最终形成累加生成数列Y（t）：

1.4.2 均值生成 将上环节生成的累加数据再次进行均值生成，并最后形成一个均值数据Z（t）：

1.4.3 建立GM（1.1）模型 首先需要建立一个Y（t）的阶线性微分方程式，即：dY（t）/dt+aY（t）=u，该方程式也就是GM（1.1）预测模型，通过对该方程式进行解答后得到：

公式中a，u均为待定的系数，可采用最小二乘法对参数的向量进行估计，然后采用矩阵方式计算后，最终生成的表达式为：

1.4.4 通过式（3）可以获得一个估计值（t）数列 其主要是由累减还原而生成的，在此基础上可获得原始数列X（t）的估计值数列：

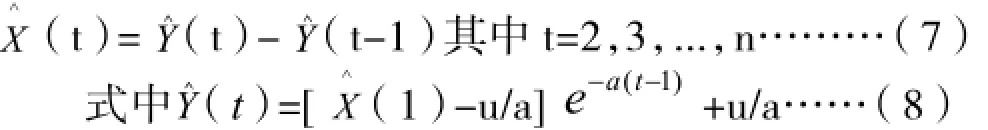
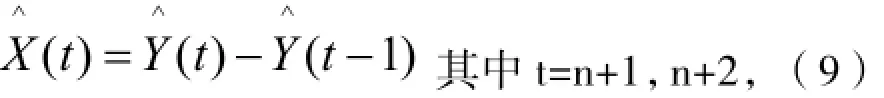
如果两个数列的拟合精确度不合符相关标准，则可以直接采用式（9）开展外推预测，但是需要进行残差修正。

1.4.6 针对GM（1，1）模型的可靠性，我们可以采用后验差比值C、小误差概率P来综合评估。

通过计算，后验差比值C和小误差概率P如下所述：

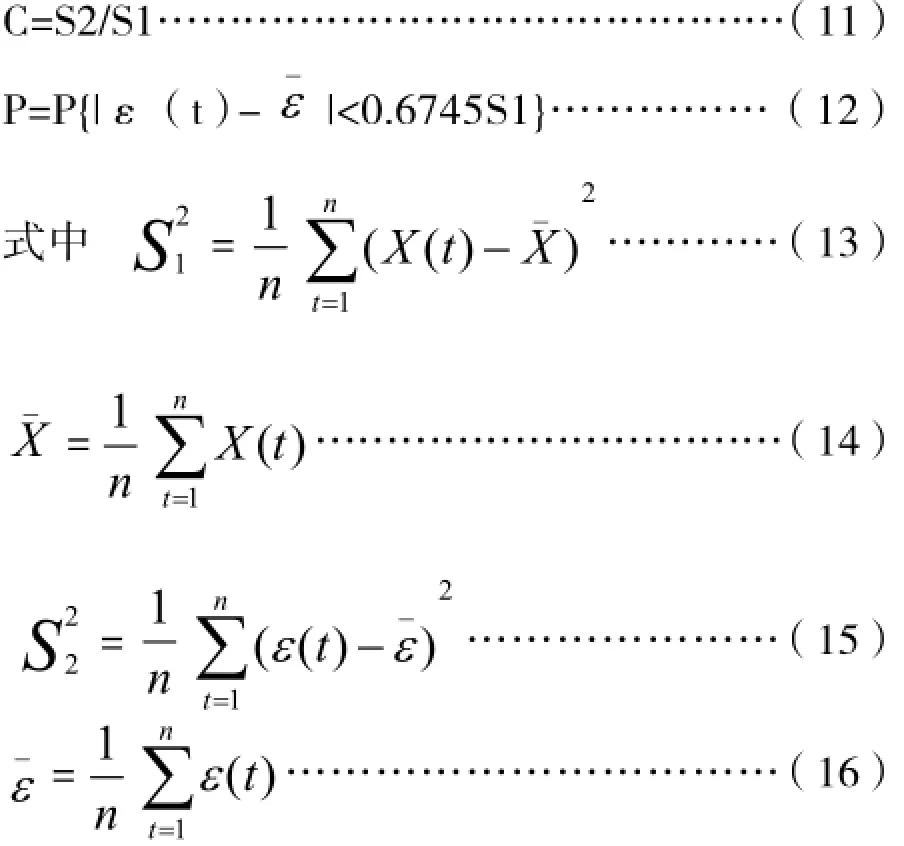
2 结果

2.1 肺结核的预测模型

根据公共卫生科学数据中心提供的2005-2012年安徽省肺结核实际发病率数据序列为X（t）=|97.8628，85.6274，88.6367，88.5044，72.1519，64.4902，62.7142，64.7939|，其序列号t为0，l，2，…7，按（4）（5）（6）式求得其D=1114291.3400，a=0.0654，u=100.2074，模型为Y（t）=-1433.7369e-0.0654（t-1）+1531.5997，当t 取不同的值，根据公式（9）即可得到相应的预测值（ t）（ 表1） 。

2.2 模型检验

根据表1 ，利用公式（13）～（16）计算S1 = 13.5746，S2 = 1.9817，后验差比值C = 0. 1460，而小概率误差P=1，依据判断标准模型的预测精确度结果显示等级为优，这样便可以开展外推预测计算。我们在实践应用中采用该模型预测分析安徽省2005 ～ 2012年肺结核发病率的拟合值、实际值如图1所示，从图形中可以看出两条曲线的吻合度比较高，这表明模型的拟合精确度较高。

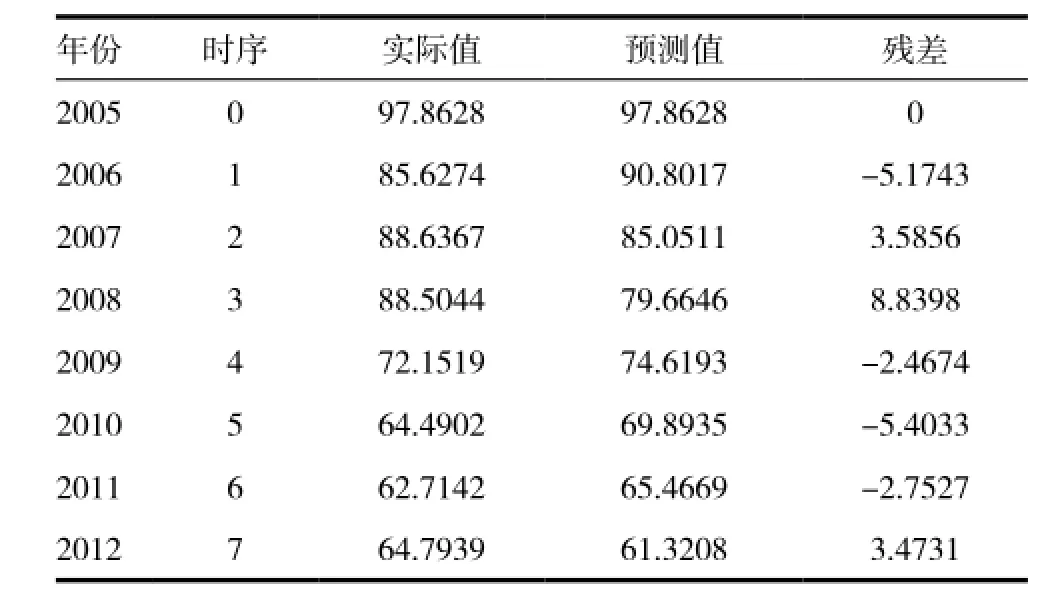
表1 2005～2012年安徽省肺结核发病率（1/10万）实际值、预测值统计分析

2.3 肺结核发病率预测结果分析

通过采用预测模型计算安徽省2005～2012年肺结核发病率的预测值，预测结果显示2005～2012年的肺结核发病率分别为57.4372/10万、 53.7996/10万和50.3923/10万，肺结核发病率整体上呈现出明显的下降趋势。

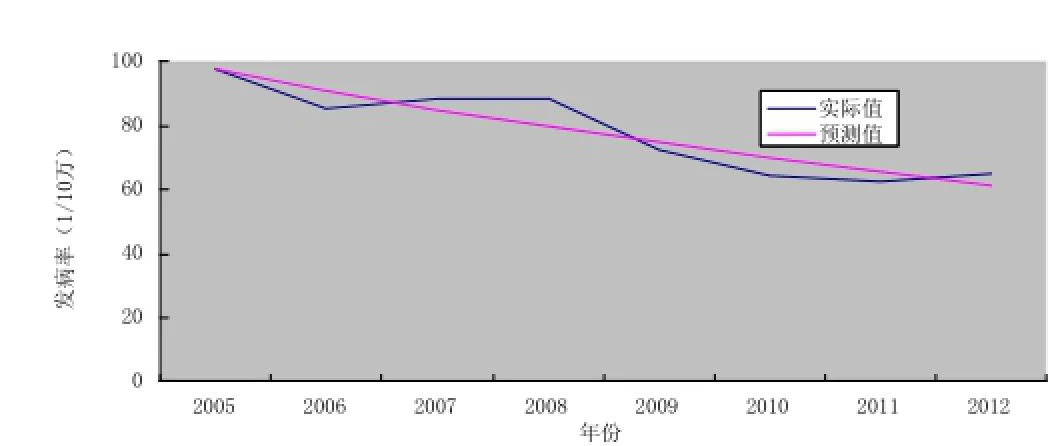
图1 2005～2012年安徽省肺结核发病率预测值、实际值

3 讨论

灰色系统理论的提出主要基于社会、经济的宏观预测、决策，而经过多年的推广、改良后逐渐被应用与医学、生命科学研究中，重点在疾病发病率、死亡率方面取得了显著成效。GM（1，1）模型经过长期实践应用证实，在区域性传染性疾病的流行趋势预测方面具有明显的优势，该模型计算简单，而且对原始数据的长度要求比较低，也就是在很短的数据系列中可以取得准确度较高的预测值。正是由于该模型具有上述优势，有效解决了其他预测方法无法对短期观察数据进行流行性预测的问题[8]。

肺结核疾病预测主要通过目前掌握的相关数据资料，利用数学模型方式对肺结核疾病未来设定时间内的发病趋势实施预测[9]。通过对疾病的发病趋势进行准确预测，有助于提升地区在疾病预防、控制方面的预见性、主动性，同时也为制定、完善相关防控机制提供理论支持[10]。灰色预测模型GM（1，1）在肺结核预测中，只需要建立一个数列即可组建预测模型，而且对样本的概率、容量无严格要求[11]；近年来，国内学者采用灰色预测模型GM（1，1）对传染性疾病进行预测，在传染性疾病流行性预测均取得了相对准确结果[12]。由此可证明，灰色预测模型GM（1，1）在疾病预测中具较强适应性、高精确度建模及良好预测性能等优势。

近年来，安徽省相关部门应制定合理的五年结核病防控规划，并在全省范围内科学、合理的结核病防控措施；另外构建结核病综合防控网络体系，健全基层医疗防控协作机制。在本文研究中，笔者采用立灰色系统GM（1，1）预测模型对2005～2012安徽省肺结核发病报告数据进行建模计算，最终得到的后验差检验结果显示预测模型准确度较高，因此该模型计算获取的预测值具有较高的参考价值，且结果显示未来几年全省范围内肺结核发病率呈明显的下降趋势，但是发病率仍然呈较高水平，这表明我省仍然需要加强结核病的防控工作。

[1] Gandhi NR，Shah NS，Hndrews JR，et al. HIV coinfection in multidrug and extensively drugresistant tuberculosis results in highearlymortality[J] Am J Rerpir Crit Care Med，2010，18（1）：80-86.

[2] 卫生部.卫生部召开新闻发布会介绍全国肺结核疫情现状[EB/OL].http：//www.gov.cn/gzdt/2011-03/21/ content-1828718.htm.

[3] 李云，穆卫明，陆建方.肺结核发病率的灰色模型预测及及时间趋势分析[J].中华疾病控制杂志，2011，15（1）：87-88.

[4] 梁红慧，农初师，黄夏萍. 灰色系统GM（ 1，1模型在隐性梅毒发病预测中的应用[J].数理医药学杂志，2012，25（1）：3-5.

[5] 程志勇，赵贺春.吉林市2010年丙型病毒性肝炎发病率的灰色系统GM（ 1，1模型预测[J]. 中国卫生工程学，2011，1（2）：158-159.

[6] 张天良.GM（1，1）模型在预测人口出生率研究中的应用[J].中国卫生统计，2000，17（2）：88.

[7] 黄洪福.灰色数列GM（1，1）模型在“EHF”发展趋势预测中的应用[J].现代预防医学，2000，7（1）：107.[8] 白燕，张思敬，马光思.基于灰色残差GM（1，1）模型的狂犬病流行趋势的预测及分析[J].西北大学学报（自然科学网络版），2006，4（4）：141-142.

[9] 钱建东，陈鸣，张靳冬，等.灰色系统GM（1，1）模型预测常州市肺结核发病趋势[J].公共卫生与预防医学，2012，23（5）：7-8.

[10] 易静，胡代玉，杨德香，等．三种预测模型在肺结核发病预测中的预测[J].中国全科医学，2012，15（13）：1495-1497．

[11] 崔国强.利用灰色系统GM（1.1）模型预测北京市怀柔区肺结核发病率[J].首都公共卫生，2014，8（3）：109-111.

[12] 吴湘.湖北省荆门市肺结核病流行趋势做灰色模型分析[A].2011年中国防痨协会全国学术会议论文集[C]. 2011：75-76.

Application of grey system model GM( 1，1) in prevention of incidence trend of pulmonary tuberculosis in Anhui Province

SONG Hongbing HONG Guanglie
Lujiang County Center for Disease Control and Prevention, Lujiang 231500, China

Objective To establish grey system GM( 1，1) model of pulmonary tuberculosis, to apply on prevention of incidence trend of pulmonary tuberculosis in Anhui Province. Methods Established grey system GM( 1，1) model of the morbidity of pulmonary tuberculosis according to the morbidity incidence reporting data of public health science data center from 2005 to 2012 in Anhui Province, at the same time to predictively analyze the morbidity of pulmonary tuberculosis through the model from 2013 to 2015 in Anhui Province. Results Through the grey system GM( 1，1) model to establish prediction model of Y（t）=-1433.7369e-0.0654（t-1）+1531.5997 which had predicted that the morbidity of pulmonary tuberculosis were 57.4372 per 0.1 million, 53.7996 per 0.1 million, and 50.3923 per 0.1 million from 2013 to 2015 in Anhui Province. Conclusion Practical application has proved that, grey system GM (1，1) model on prevention of incidence trend of pulmonary tuberculosis in Anhui Province is accord with currently development, is worthy of higher referenced application value.

Tuberculosis; GM( 1，1) model; Anhui province; Prevention

R521

B

2095-0616（2015）08-208-04

2014-11-17）