高速精密数控车床床鞍结构参数多目标优化

段明德，李 言，冯浩亮，张壮雅，雷贤卿，刘康华

（1.西安理工大学 机械与精密仪器工程学院，陕西 西安 710048；2.河南科技大学 机电工程学院，河南 洛阳 471003）

0 引言

床鞍作为数控车床进给系统的关键部件，在加工过程中，既要传导来自丝杠螺母结合面的动态驱动力，又要承受来自刀架的动态载荷和导轨处的摩擦力，床鞍的微小振动会影响精密或超精密加工的精度，尤其在高速切削和高速进给的条件下影响更大；而床鞍的结构参数则直接影响到床鞍的动态性能。目前对机床关键部件的设计方法主要有经验类比法和有限元分析法，其中前者为传统设计方法，主要依赖于设计者的工程经验，设计结果往往不能满足现代制造对机床高性能和轻量化的设计要求。伴随着有限元理论与分析软件的发展，机床设计和研究人员逐渐将有限元分析技术引入高端数控机床的研发设计中。Berczynski等［1］对机床动态特性进行了数学建模，并应用单脉冲激振方法进行了动态特性试验；Son等［2］对机床的动态特性进行了有限元分析和相应的动态试验，分析了振动对机床加工的影响，并给出优化方案；Ohta等［3］对机床滚动导轨的16种模态进行了仿真计算和实验验证，对提高机床动态特性有较大意义；苏宇锋［4］、李杰［5］等利用有限 元法对某型号车铣复合加工中心的床鞍进行了结构优化设 计；马雅丽［6］、孙 谦［7］、张永存［8］等在有 限元方法基础上，将拓扑优化设计理论与结构设计相结合，对机床床鞍结构进行了优化设计，满足了床鞍的轻量化设计要求。虽然基于有限元分析方法对高档机床关键部件进行优化设计具有重要的实际应用价值，促进了机床优化设计方法的发展，但是由于机床结构的复杂性，上述研究的单目标优化设计方法很难获得满意的结果，往往在满足机床关键部件轻量化设计的同时会导致其抗振性下降，因此如何从一系列结构尺寸变化范围内选出有利于机床动态特性的一组参数，同时满足轻量化设计，实现机床关键部件的多目标优化设计，是亟待解决的问题。

ADGM35高速精密数控车床是国家科技重大专项立项研制的产品，车床最大回转直径为Φ400～630mm，车削主轴最高转速为4 000～8 000r／min，X／Z轴的快速进给速度要求大于等于40／60 m／min，X／Z轴的重 复定位 精度要 求小于等于0.003／0.005mm。本文以ADGM35 的床鞍为对象，提出一种基于结构参数灵敏度分析、结合粒子群算法和模糊综合评判法指导床鞍部件优化设计的方法。首先根据灵敏度分析法确定床鞍几何参数对床鞍动态特性的影响规律；然后以床鞍的前两阶固有频率和质量为优化目标，建立多目标优化方程；最后结合粒子群算法和模糊综合评判法优化求解方程，以实现床鞍结构的多目标优化设计。

1 模态分析和优化目标的确定

高速数控车床床鞍的结构参数和质量对其动态特性有重要影响，固有频率是表示机床结构动态特性的指标之一。机床加工过程中，激振频率与固有频率一致时会引起共振，定量分析床鞍的主要结构参数对固有频率的影响，是合理设计床鞍结构和提高床鞍动态性能的前提。本文研究的ADGM35高速精密数控车床床鞍采用十字结构的布局形式（如图1），由机床设计参数和机床设计手册得到主要结构参数，如表1所示。

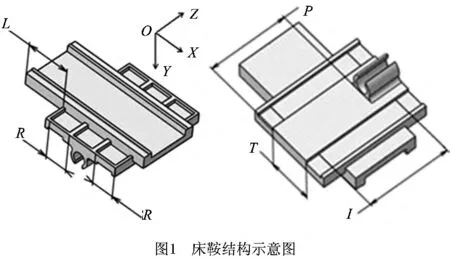
表1 床鞍结构参数

床鞍下部通过导轨与床身相连，并由丝杠牵引运动，上部通过滑动导轨与滑座和刀架连接在一起，滑座可以沿导轨移动。本文重点研究床鞍的动态特性，不考虑床鞍受上部刀架力的因素，床鞍主要承受与床身连接的导轨的约束和相应的丝杠约束。导轨的约束限制床鞍X方向和Y方向的位移，而丝杠约束限制了床鞍沿着导轨滑动方向即Z方向的位移。考虑到床鞍结构的复杂性，在不影响有限元计算结果的前提下，建模时对模型进行了必要地简化，如忽略倒角、圆角、螺纹孔和小凸台等。在有限元软件ANSYS WORKBENCH中设置床鞍材料属性为：密度为7.8×103kg／m3，弹性模量为2.07×105MPa，泊松比为0.3，屈服应力为235N／mm2。

对三维模型进行网格划分，完成网格划分后的床鞍模型如图2 所示。该模型共有8 062 个节点，4 379 个实体单元，其模态分析结果如表2所示。

表2 初始设计床鞍1阶～3阶固有频率和相应振型

由表2的模态分析结果可以看出，床鞍的前三阶固有频率均在300Hz以上，床鞍具备一定的低阶固有频率，但为了避免床鞍的固有频率与外界激励频率耦合发生共振，致使工件表面形成加工振纹而影响加工的精度和效率，需要对床鞍的结构进行进一步优化设计，以使床鞍的固有频率远离激振频率，为机床的提速预留空间。

对比前三阶固有频率的分析结果可以看出，低阶模态频率（300.9 Hz）对床鞍结构动力性能的影响远远大于高阶模态（549.5 Hz），因此本文略去对床鞍高阶模态的描述，以床鞍的前两阶固有频率f1、f2和质量m作为床鞍的优化目标，对床鞍结构进行优化设计。

2 设计变量的选取

为保证床鞍的动态特性，本文提出一种基于灵敏度［9-10］分析来指导床鞍部件优化设计的方法。所谓灵敏度分析是指输出变化对周围条件变化的敏感程度，其数学意义为：对于函数g=g（x1，x2，…，xn），函数值g对变量xi变化的灵敏程度，即

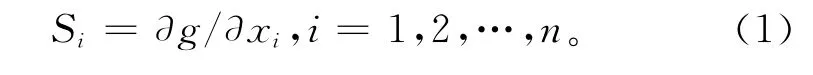
对于床鞍结构参数的灵敏度分析，函数g可表示床鞍结构的固有频率、质量等性能指标；变量xi为导轨悬伸、导轨跨距、滑块间距、筋板位置和丝杠座位置等结构参数；灵敏度值Si为结构参数变化对床鞍性能指标的影响程度。

2.1 一阶固有频率对床鞍结构参数的灵敏度分析

采用第1章中的有限元分析方法，以导轨悬伸、导轨跨距、滑块间距、筋板位置和丝杠座位置为结构参数，分析得到床鞍的一阶固有频率如图3所示。

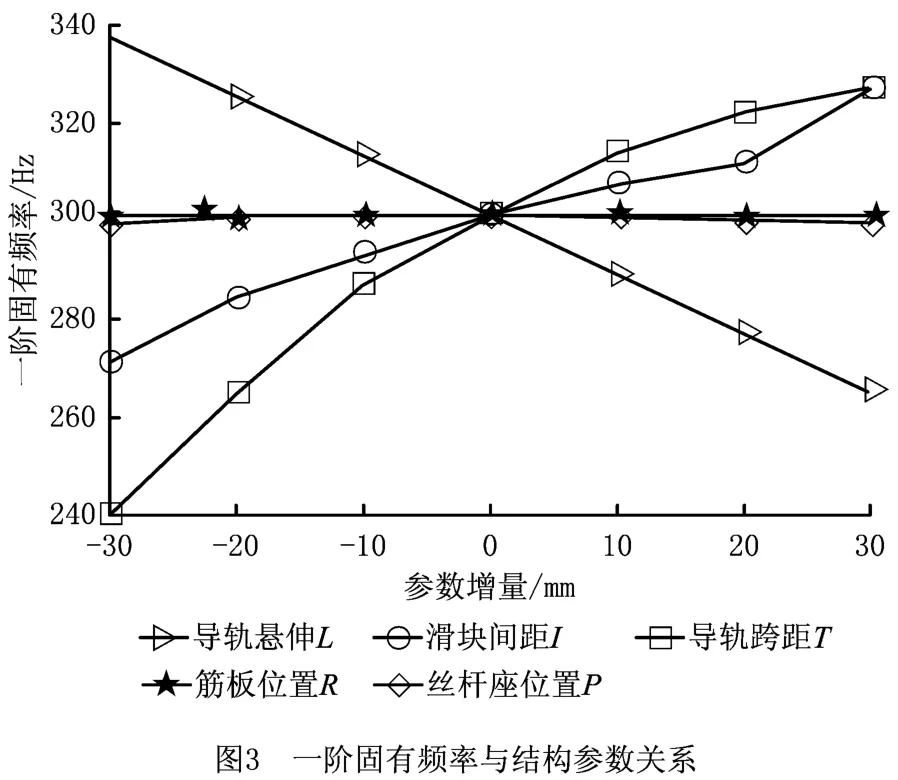
对图3中的一阶固有频率与结构参数灵敏度曲线做二次函数拟合，所得到的床鞍一阶固有频率f1与各参数增量之间的函数关系为

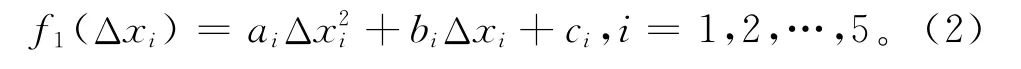
式中：ai，bi和ci为拟合函数的系数；Δxi为各参数的增量。

根据式（1）对式（2）求导，计算得到床鞍一阶固有频率对各结构参数的灵敏度

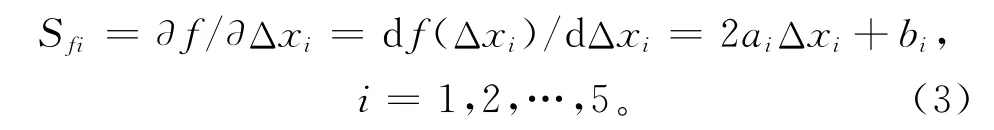
式中Sfi为床鞍一阶固有频率对各参数的灵敏度，用矩阵形式可表示为

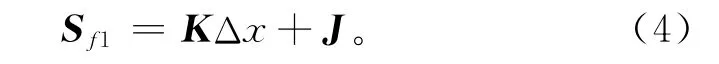
式中：Sf1，K和J分别为式（4）中Sfi，2ai，bi的向量表示形式，对应的向量K，J分别为

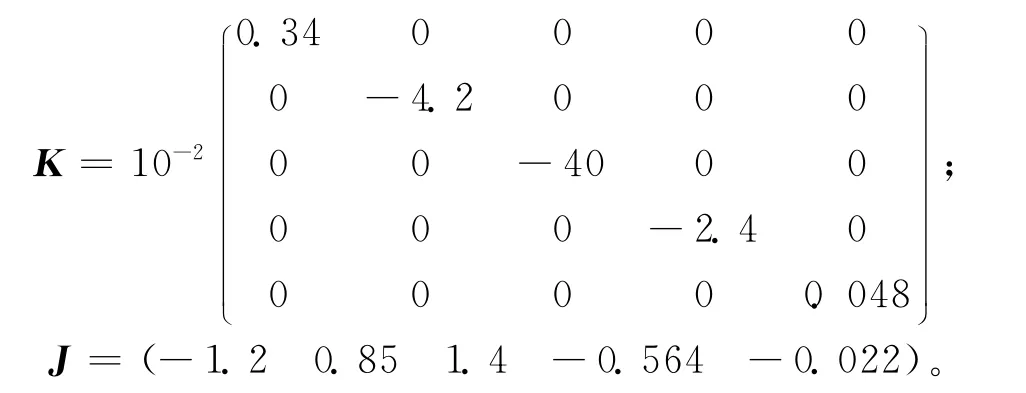
将Δxi代入式（5），计算出床鞍一阶固有频率f1对各结构参数的灵敏度为

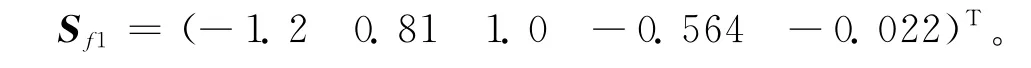
由上述灵敏度分析理论可知，床鞍一阶固有频率对各结构参数灵敏度的大小排序为：导轨悬伸L＞导轨跨距T＞滑块间距I＞丝杠座位置P＞筋板位置R。

2.2 二阶固有频率对床鞍结构参数的灵敏度分析

二阶固有频率与各结构参数的灵敏度曲线如图4所示。

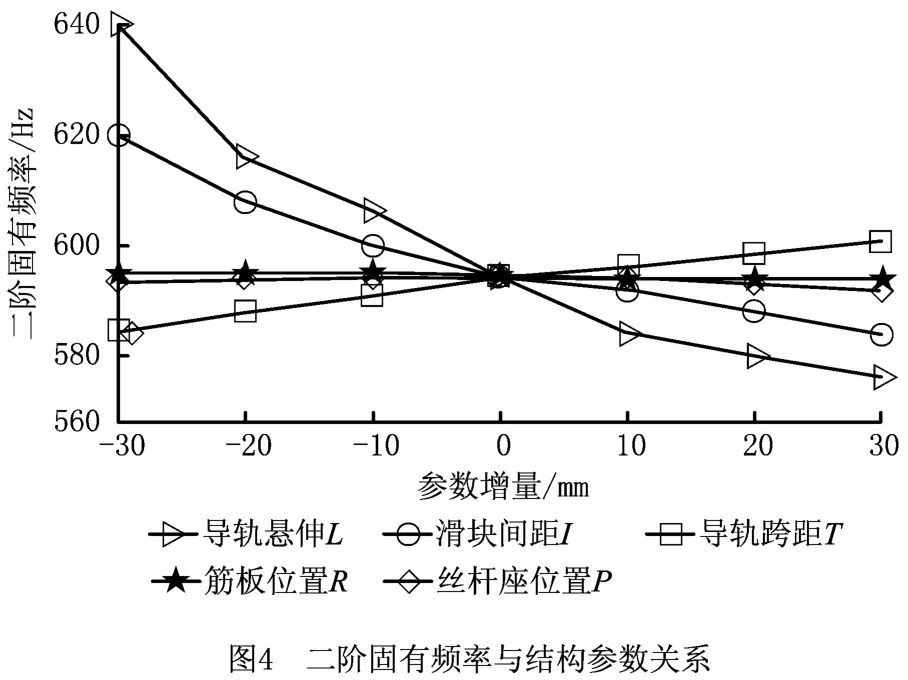
同理，由图4可以计算出床鞍二阶固有频率f2对各结构参数的灵敏度矩阵为

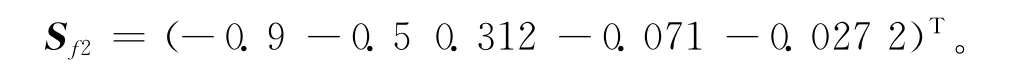
由此可知床鞍二阶固有频率对各结构参数灵敏度的大小排序为：导轨悬伸L＞滑块间距I＞导轨跨距T＞丝杠座位置P＞筋板位置R。

2.3 床鞍质量对床鞍结构参数的灵敏度分析

从图5可以计算出床鞍质量m对各结构参数的灵敏度矩阵为

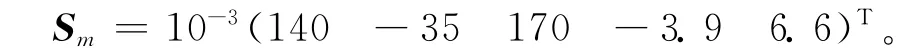
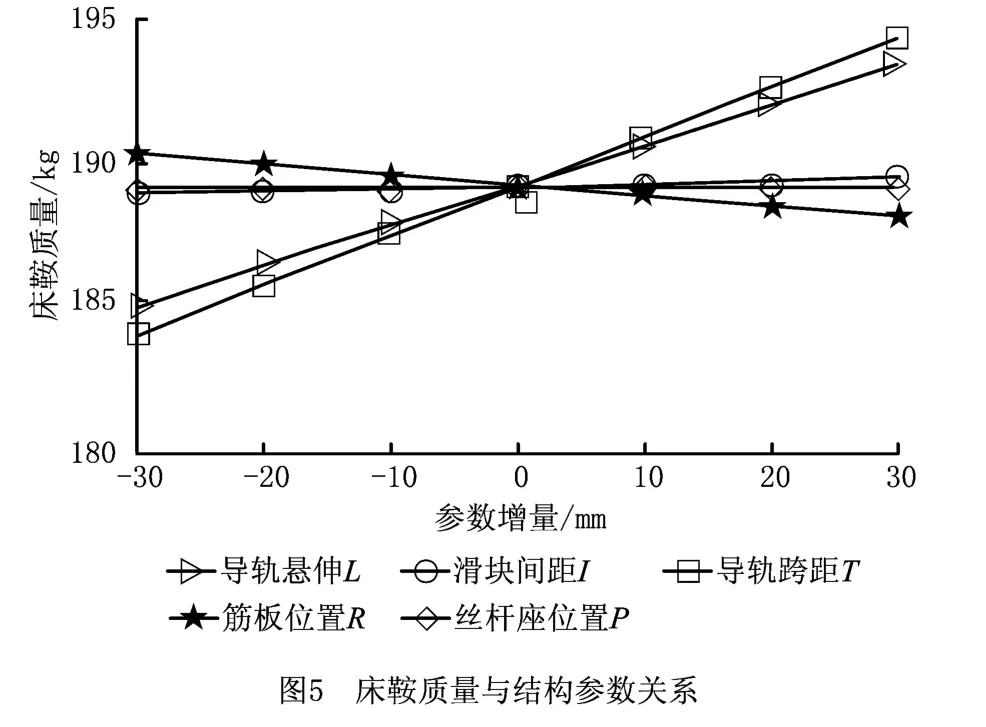
由此可知，床鞍质量对各结构参数灵敏度的大小排序为：导轨跨距T＞导轨悬伸L＞滑块间距I＞丝杠座位置P＞筋板位置R。

从Sf1，Sf2和Sm的灵敏度计算结果可以看出，丝杠座位置P和筋板位置R参数的变化对床鞍的一、二阶固有频率及质量的影响很小，可以忽略不计，因此本文选取L，T和I为本次多目标优化的设计变量。

2.4 灵敏度分析试验验证

为验证上述结构参数灵敏度分析结果的可靠性，对床鞍进行试验分析，所设计的床鞍试验装置如图6所示，图中用上板一端悬出下板的长度代替床鞍尾架的长度，在楔形块上的螺栓松开时可以使上板在下板的凹型槽上移动，通过移动上板悬出下板的长度来提供不同尾架长度的参数；导轨跨距参数调整槽与滑块上的螺纹孔通过螺栓连接，可以通过U 型槽的设置改变滑块的安装位置，整个试验台安装在带T 型槽的滑轨上，以此完成不同导轨跨距下的模态参数变化规律试验。

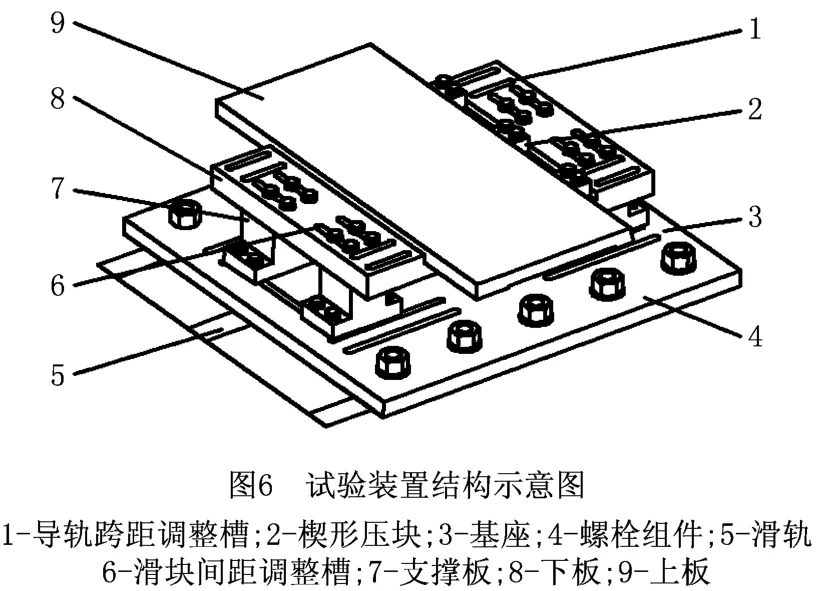
试验设备选用Preamx测试系统、EA-YD-1181单向振动加速度传感器、YE-5852型电荷放大器和LC-40A 型力锤，床鞍模态试验测试如图7所示。

试验中采用单点敲击、多点测试的方法进行数据采集。实验前将基座固定在滑轨上，在上板和支撑板上的相应位置贴上加速度传感器，然后由力锤敲击提供激励信号，在大频率范围内进行扫描，在较短的时间内找出频率所在的频率段，最后测试出床鞍结构的固有频率，测试结果如图8所示。

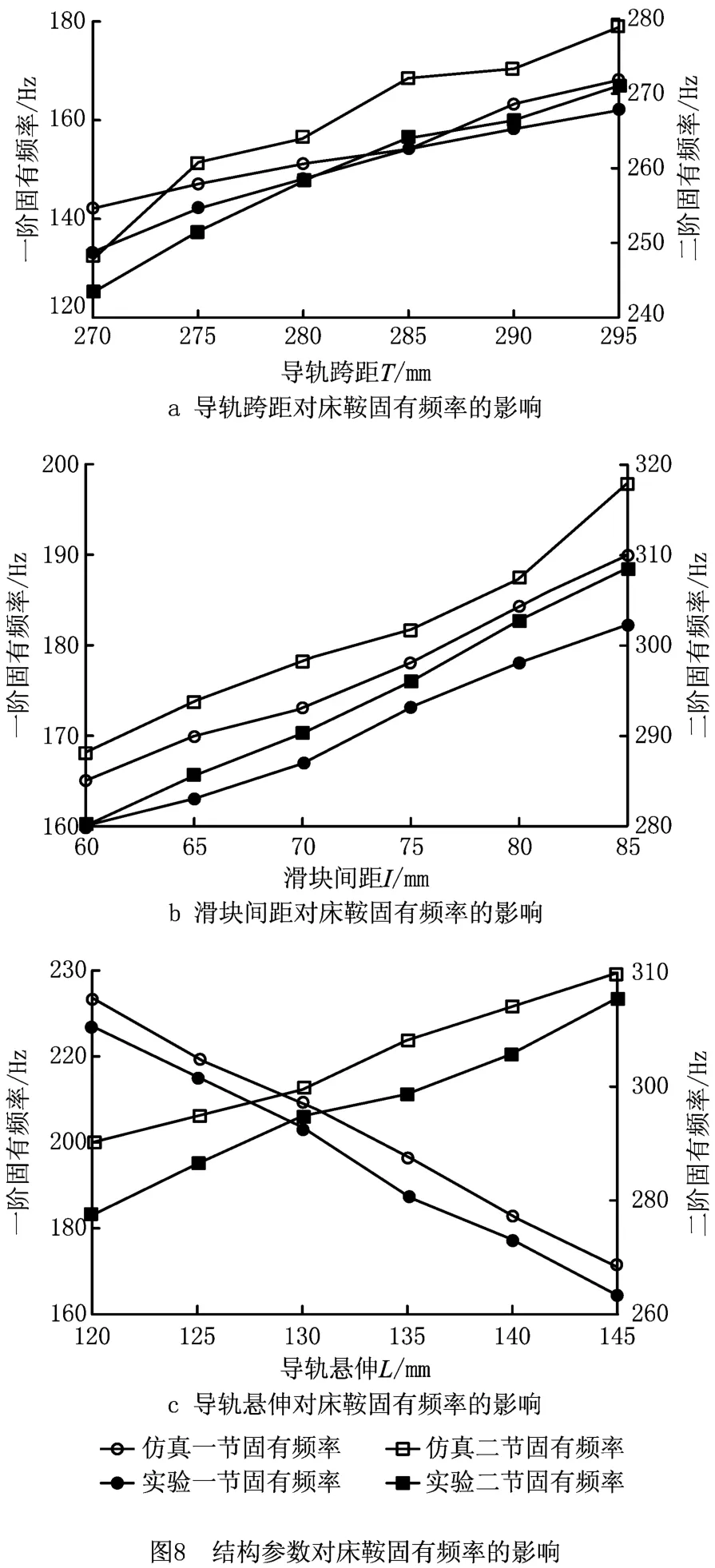
从图8的分析试验结果可以看出，导轨悬伸L、导轨跨距T、滑块间距I三个结构参数对床鞍试验装置固有频率的影响规律基本与试验结果吻合，能较准确地反映参数对床鞍试验装置固有频率的影响规律，其固有频率值误差不超过5%，灵敏度误差不超过10%。由于本文研究的是床鞍参数变化对床鞍固有频率的影响，实验装置采用了多层可调结构设计，这是一个整体的结构，这种形式会造成试验装置刚度降低，这也是本文的仿真结果与试验装置固有频率产生误差的原因。

综上分析，选择导轨悬伸L、导轨跨距T、滑块间距I三个参数作为床鞍多目标优化设计的变量。

3 床鞍结构参数多目标建模与优化

3.1 多目标优化函数的确定

将结构优化设计这一实际工程问题抽象为适当的数学模型，是工程优化设计的关键。根据第1章和第2章的分析和结论，以床鞍的前两阶固有频率f1，f2和质量m为优化目标，以导轨悬伸L、导轨跨距T、滑块间距I为设计变量。对于模态频率，本文定义目标函数为这两个物理量的平方和，求总和的最大值，即

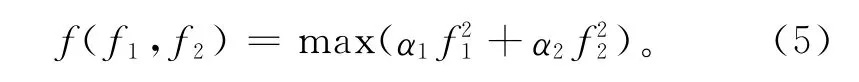
为求解方便，引入一个大数Q，将式（5）中求解的最大值转化为求解最小值的新函数，建立多目标优化数学模型：

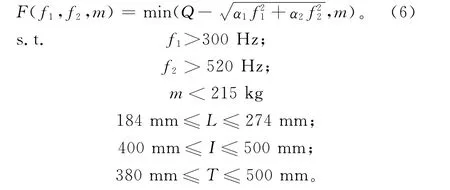
式中：Q取值为800Hz；α1和α2为两阶固有频率的权重系数，根据其重要程度采用专家打分法取α1=0.8，α2=0.2。

3.2 基于粒子群算法的床鞍优化模型的求解

粒子群优化（Particle Swarm Optimization，PSO）算法［11-12］是一种基于群智能的全局优化算法，能以较大的概率找到优化问题的解。令向量Xi=［Li，Ii，Ti］为床鞍结构设计问题中的一个非劣解，则PSO 算法中的粒子群即为每一个非劣解（向量Xi）构成的集合N=｛Xi，i=1，2，…，m｝。根据PSO算法，群体中每一个粒子的解为

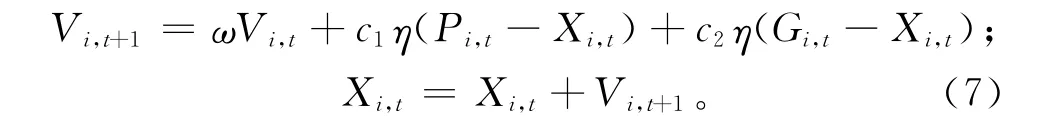
式中：c1，c2和η为学习因子；Pi，t为粒子群N中第i个粒子在前t次寻优过程中找到的最优解；Gi，t为粒子群N在前t次寻优过程中找到的共同最优解；ω为惯性因子，

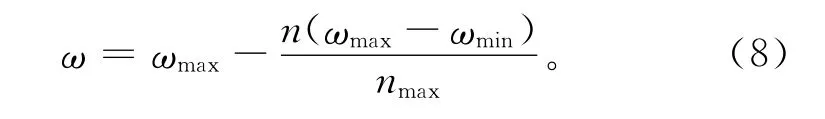
式中：n为迭代次数；nmax为最大迭代次数；ωmax和ωmin分别为ω的最大值和最小值。

本案例问题中，PSO 算法参数为：粒子群规模N=40，学习因子c1=c2=0.6，最大迭代次数G=200，最终得到的非劣解如表3所示。

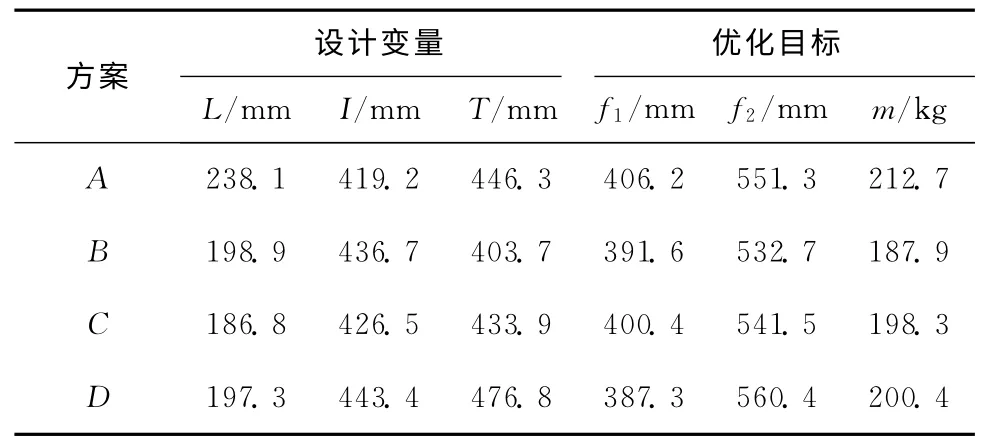
表3 非劣解

由表3可知，4个优化目标都有最优的单目标方案，但是单个目标函数的最优方案与其他优化方案均不相同，在满足其中一个目标最优的同时，其他目标会受其影响。因此，需要确定出床鞍结构整体优化的多目标优化方案。

3.3 基于模糊综合评判法的床鞍最优方案确定

模糊综合评判法［13-14］是构建一个评判矩阵来表示全部评判对象的特性，再依据评判函数，针对各个对象的不同赋予相应的评判指标，评判指标排序不同表示各个对象的优劣程度不同，根据排序先后选出其中的最优方案。模糊综合评判法综合考虑了全部因素对优化目标的影响而评判出最优解，可以较好地解决目标函数的多变量（导轨悬伸L、导轨跨距T、滑块间距I）难以量化的问题。

（1）对象集、因素集的确定

以3.2 节的床鞍优化求解方案为对象集X=｛A，B，C，D｝，其因素集为U=｛α1f1+α2f2，1／m｝，则四种评价方案如表4所示。

表4 评价方案

（2）评判矩阵的确定

根据表4中的优化方案确定评判矩阵。例如优化方案A中的前两阶加权固有频率α1f1+α2f2最佳，计算所得频率值为467.2 Hz，则其特性指标为467.2／467.2=1.00，方案B的特性指标为443.8／467.2=0.950。同理，其他特性指标依照上述方法计算，得到的评判矩阵为

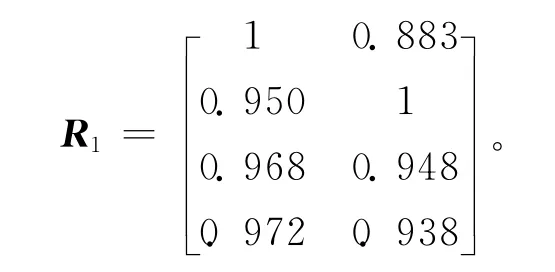
（3）评判函数确定

根据实际问题的不同，通常使用的评判函数有：

1）Ⅰ型

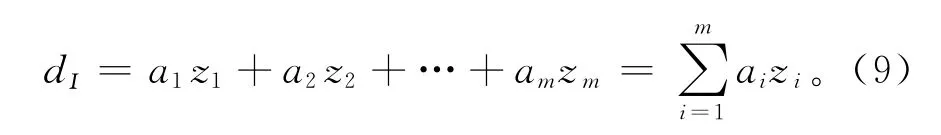
式中a1+a2+…+am=1，ai≥0，i=1，2，…，m。

2）Ⅱ型

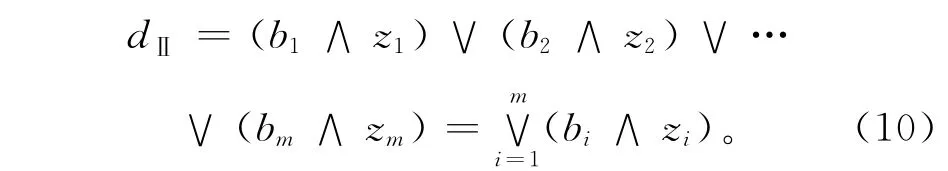
式中0≤bi≤1，i=1，2，…，m。

3）Ⅲ型

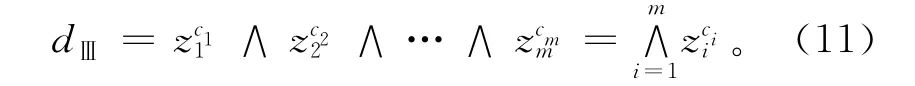
式中ci＞0，i=1，2，…，m。

系数ai，bi和ci是对各因素作加权处理的权数。Ⅰ型函数是加权平均法，综合考虑了对象的各项特征指标；Ⅱ型函数是在权数限定下，将最大的特征指标作为评判指标；Ⅲ型函数则是将最小的特征指标作为评判指标。本文根据床鞍优化问题的实际情况，综合三种评判函数的优点，根据评判矩阵R1计算出评判指标，构成二级评判矩阵，进行二级模糊综合评判。

（4）评价指标的计算

根据床鞍的设计要求以及各参数对床鞍性能的影响，各型评判函数的权重系数赋值为：Ⅰ型cⅠ=［0.50，0.20］T，Ⅱ型cⅡ=［0.95，0.80］T，Ⅲ型cⅢ=［1.00，1.00］T，由此可求得各评判指标如下：

Ⅰ型评判指标

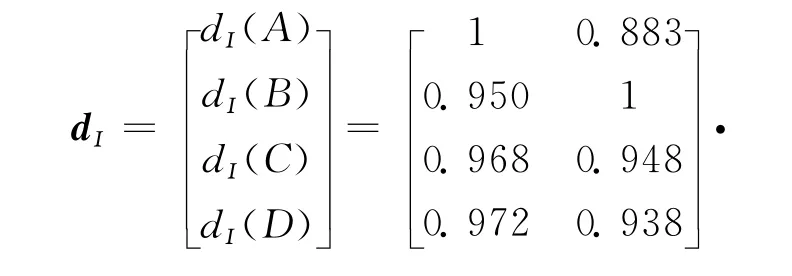
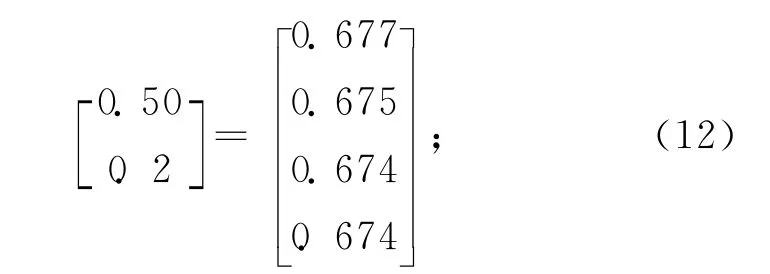
Ⅱ型评判指标

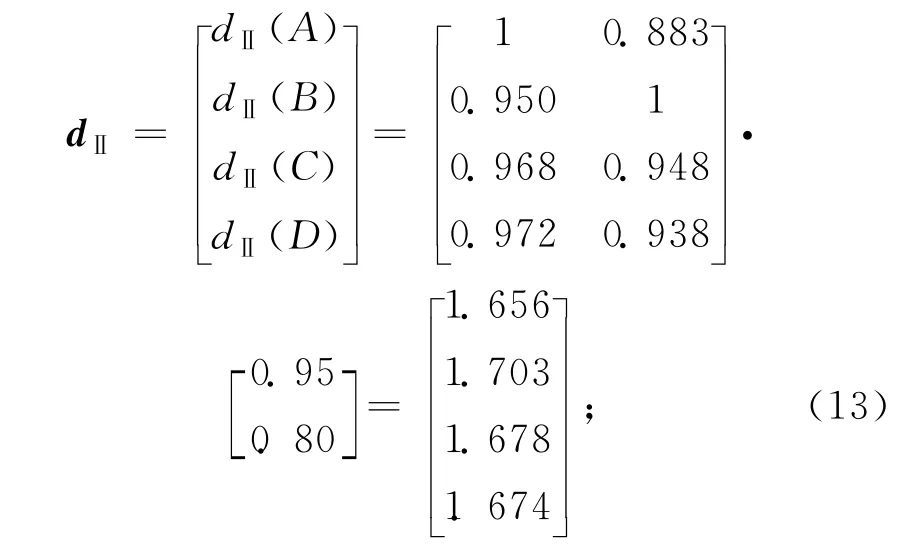
Ⅲ型评判指标

二级评判矩阵

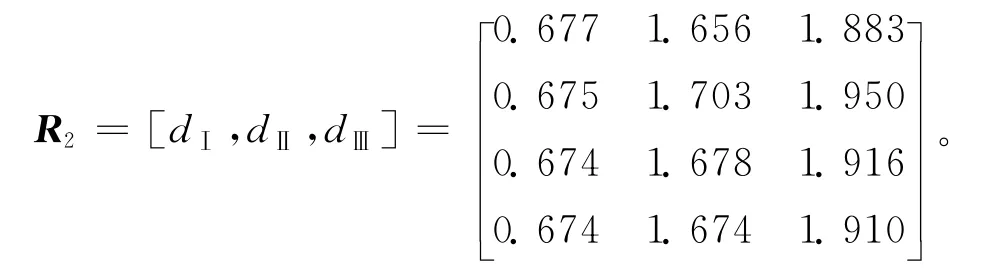
对得到的二级评判矩阵求平均值，得到二级模糊综合评判指标为

表4中的四种评价方案计算完毕，得出优劣顺序依次是B，C，D，A，其中方案B最优，最终优化结果如表5所示。

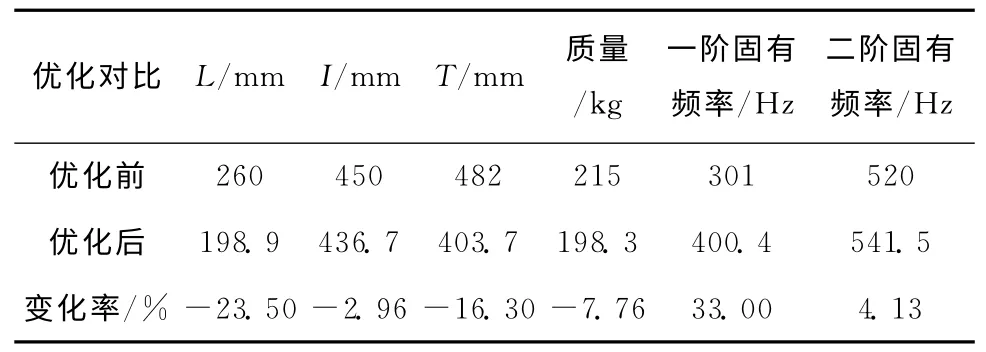
表5 床鞍优化前后的对比

从表5中可以看出，对床鞍的导轨悬伸L、导轨跨距T和滑块间距I进行优化设计，在床鞍质量降低7.76%的情况下，其一阶固有频率提高33%，二阶固有频率提高4.13%，达到了优化目的。

4 谐响应分析

在模态分析的基础上，对优化后的床鞍结构进行谐响应分析［15-16］，得到床鞍最大变形处的y向位移和相位角。求解条件为：在导轨上沿Y轴方向施加激振力，其幅值为500N，相位角为30°，求解频段设为0～600 Hz。采用动柔度表达结构的传递函数［17-18］，与优化前的设计结构进行对比，得到的结果如图9所示。

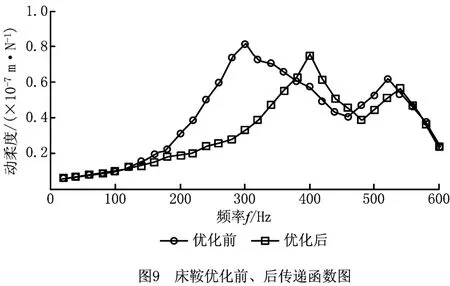
通过图9可知，床鞍在y向第一次共振时的最大动柔度降低8.60%左右，第二次共振动时的最大动柔度降低9.06%左右。

5 结束语

本文通过模态分析得到床鞍的前三阶固有频率和振型。为了提高高速车床床鞍的动态性能，确定床鞍固有频率和床鞍质量为优化目标。

通过机床床鞍结构的动态特性灵敏度分析，确定了床鞍主要设计参数的灵敏度及其对床鞍动态性能的影响规律，并通过模态试验验证了分析结果的可靠性。

依据灵敏度分析的结果，选择对床鞍动态性能影响最大的导轨悬伸L、导轨跨距T、滑块间距I等床鞍结构参数为优化变量，以床鞍的前两阶固有频率和质量作为优化目标，采用PSO算法和模糊综合评判法相结合的方法对床鞍结构参数进行了多目标优化，结果表明：一阶固有频率提高了33%，二阶固有频率提高了4.13%，质量减轻了7.76%，即床鞍在其动态性能得到提升的同时减轻了质量，达到了优化的目的。

本文的研究工作是在基于传统设计方法设计的床鞍的基础结构上进行的。探索基于拓扑优化、尺寸及形状优化的混合设计方法解决床鞍的结构优化问题，实现机床基础部件的最佳的结构布局和结构参数，是下一步要展开的工作。

［1］BERCZYNSKI S，GUTOWSKI P.Identication of the dynamic models of machine tool supporting systems［J］.Journal of Vibration and Control，2006，13（3）：257-277.

［2］SON H S，CHOI H J，PARK H W.Design and dynamic analysis of an arch-type desktop reconfigurable machine［J］.International Journal of Machine Tools and Manufacture，2010，50（6）：575-584.

［3］OHTA H，HAYASHI E.Vibration of linear guideway type recirculating linear ball bearings［J］.Journal of Sound and Vibration，2000，235（5）：847-861.

［4］SU Yufeng，YUAN Wenxin，LIU Deping，et al.Thermal characteristics of the saddle of high speed turn-milling combined CNC machine center［J］.Modular Machine Tool &Automatic Manufacturing Technique，2011（4）：31-32，36（in Chinese）.［苏宇锋，袁文信，刘德平，等.高速车铣复合加工中心床鞍的热态特性分析［J］.组合机床与自动化加工技术，2011（4）：31-32，36.］

［5］LI Jie，LIU Deping，SU Yufeng，et al.Temperature field modeling and thermal deformation analyzing for saddle in high-speed milling［J］.Machinery Design &Manufacture，2011（7）：211-212（in Chinese）.［李 杰，刘德平，苏宇锋，等.高速铣削床鞍温度场建模与热变形分析［J］.机械设计与制造，2011（7）：211-212.］

［6］MA Yali，ZHAO Erxin，ZHAO Hong’an，et al.The light-weight design of turning center saddle bed based on topology optimization［J］.Machine Design &Research，2011（3）：103-107（in Chinese）.［马雅丽，赵二鑫，赵宏安，等.拓扑优化的数控车削中心床鞍轻量化设计［J］.机械设计与研究，2011（3）：103-107.］

［7］SUN Qian.The study of optimization in elastic constrain condition and the modular structural design of the saddle bed［D］.Dalian：Dalian University of Technology，2012（in Chinese）.［孙 谦.弹性约束优化方法研究及床鞍单元化结构设计［D］.大连：大连理工大学，2012.］

［8］ZHANG Yongcun，CUI Lei，ZHOU Lingfeng，et al.Innovative stractural design for bed saddle of machine based on topol-ogy optimization［J］.Chinese Journal of Solid Mechanics，2011，32（S1）：335-342（in Chinese）.［张永存，崔 雷，周玲丰，等.基于拓扑优化的机床床鞍创新构型设计［J］.固体力学学报，2011，32（S1）：335-342.］

［9］DANG Yaoguo，ZHU Jianjun，LI Bangyi.Operational research［M］.Beijing：Science Press，2012（in Chinese）.［党耀国，朱建军，李帮义.运筹学［M］.北京：科学出版社，2012.］

［10］LU Lingyun.Reseach on sensitivity analysis methods and toll based on simulation experiments［D］.Harbin：Harbin Institute of Technology，2013（in Chinese）.［陆凌云.基于仿真实验的灵敏度分析方法及工具研究［D］.哈尔滨：哈尔滨工业大学，2013.］

［11］LI Li，NIU Ben.Partical swarm optimization［M］.Beijing：Metallurgical Industry Press，2009（in Chinese）.［李 丽，牛奔.粒子群优化算法［M］.北京：冶金工业出版社，2009.］

［12］ZHENG Jinxing.Application of particle-swarm-optimizationtrained artificial neural network in high speed milling force modeling［J］.Computer Integrated Manufacturing Systems，2008，14（9）：1710-1716（in Chinese）.［郑金兴.粒子群优化人工神经网络在高速铣削力建模中的应用［J］.计算机集成制造系统，2008，14（9）：1710-1716.］

［13］LING Yun，JI Shuping，MA Yulin，et al.A new design method of tolercance allocation［J］.Computer Integrated Manufacturing Systems，2000，6（1）：86-92（in Chinese）.［凌 芸，姬舒平，马玉林，等.一种基于模糊综合评判的设计方法［J］.计算机集成制造系统，2000，6（1）：86-92.］

［14］LIANG Jin，CHEN Xiongda，ZHANG Hualong，et al.Mathematical modeling［M］.Shanghai：Shanghai Scientific &Technology Publishers，2014（in Chinese）.［梁 进，陈雄达，张华隆，等.数学建模［M］.上海：上海科学技术出版社，2014.］

［15］SU Xunwen，WANG Shaoping，ZHU Dongmei，et al.Harmonic analysis and optimized vibration sensor locations of the helicopter intermediate gearbox［J］.Journal of Beijing University of Aeronautics and Astronautics，2011，37（9）：1049-1053（in Chinese）.［苏勋文，王少萍，朱冬梅，等.直升机中减速器谐响应分析与传感器优化布局［J］.北京航空航天大学学报，2011，37（9）：1049-1053.］

［16］YU Changliang，ZHANG Hui，WANG Renche，et al.Study on method for weak link identification of dynamic stiffness of a machine tool and optimization design［J］.Journal of Mechanical Engineering，2013，49（21）：11-17（in Chinese）.［于长亮，张 辉，王仁彻，等.机床整机动刚度薄弱环节辨识与优化方法研究［J］.机械工程学报，2013，49（21）：11-17.］

［17］YANG Su，TANG Hengling，LIAO Boyu，et al.Machine dynamics（Ⅰ）［M］.Beijing：China Machine Press，1983（in Chinese）.［杨 橚，唐恒龄，廖伯瑜，等.机床动力学（Ⅰ）［M］.北京：机械工业出版社，1983.］

［18］CAO Shuqian，CHEN Yushu，DING Qian，et al.Transfer function technique of dynamic balancing for high-speed rotors［J］.Journal of Mechanical Strength，2002，24（4）：500-504（in Chinese）.［曹树谦，陈予恕，丁 千，等.高速转子动平衡的传递函数法［J］.机械强度，2002，24（4）：500-504.］