基于HFSS同轴线式液位传感器的仿真

王金华， 尤丽华， 安 伟， 吴静静

(江南大学机械工程学院，江苏无锡214122)

随着科学技术的发展，尤其是计算机技术与通信技术的高速发展，液位测量的原理和方法也在不断发展和更新。在更多的液位检测场合下，对液位测量的准确度、响应性等有了更高的要求，传统的浮子式、电阻式、电容式、超声波、磁致伸缩式等液位传感器已不能满足测量的要求。

目前国内一部分原油含水率的检测方法为同轴线式相位法［1-2］，国外也有使用同轴探针进行密度测量的研究［3］，使用同轴线式传感器进行液面高度测量的研究却很少。电磁波在不同介质中传播特性主要取决于液体的相对介电常数和电导率，利用电磁波在同轴线内传播时产生的相位移和幅度衰减，可以成为测量液面高度的一种有效方法。文中根据同轴线内电磁波的传播理论，对同轴相位法测量液面高度进行理论推导。利用电磁仿真软件HFSS对不同频率不同介质溶液下的同轴线式传感器建模并仿真，可以得到同轴线式传感器两端面的相位差的计算结果和同轴线式传感器内部的电磁场分布情况。

1 同轴线式传感器理论分析

1．1 电磁波的传播

电磁波是由同相且互相垂直的电场与磁场在空间中衍生发生的振荡粒子波，即为传播着的时变电磁场。通过麦克斯韦方程可以发现，一个随时间变化电场可以产生一个随时间变化的磁场，而交变的磁场又能产生交变的电场，此类交变的电场、磁场互相产生的现象是会无限循环下去的。在这种互相转变的过程中，它们便会脱离场源，由近及远地传播出去，也就产生了电磁波［4］。

电磁波在导电媒质中的传播常数由介质的介电常数和电导率决定，其传播常数可以表示为［5-6］

其中:γ为电磁波的传播常数，是反映经过单位长度传输线后波的幅度和相位变化的物理量;α称为衰减系数，表示传输线上行波传播单位长度幅值的变化，其单位为1/m或dB/m;β为相移常数，表示传输线上行波传播单位长度相位的变化，其单位为1/m或rad/m。衰减常数α和相位移常数β分别由式(2)和式(3)表示:

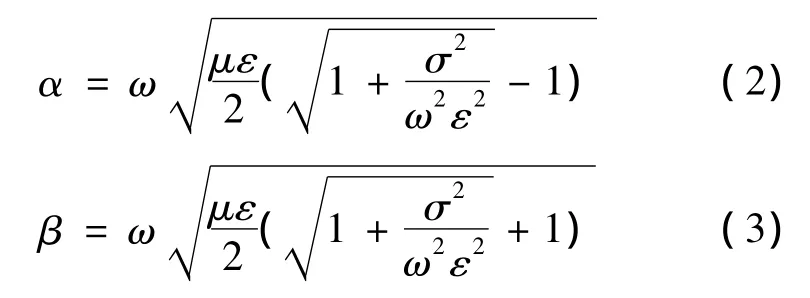
式中:ω为电磁波的角频率;ε为媒质的介电常数;μ为媒质的磁导率;σ为媒质的电导率。

通过式(2)和式(3)可以发现，在一定电磁波发生频率下，溶液中电磁波的衰减常数σ和相位移常数β为常数。同时，电磁波的发射频率越高，则相位移常数β的值越大，在定长位移上相位变化值越大。

1．2 同轴相位法的基本原理

一般情况下，液体多为非铁磁性材料，其相对磁导率趋近于1，但是相对介电常数的值却各不相同。在相同电磁波发射频率的条件下，相对介电常数成为影响相移常数变化的主要因素。例如，在温度20℃ 条件下，空气的介电常数近似为1，而水的介电常数约为81，相对介电常数的差值明显。电磁波的传播特性受到介电常数变化的影响，使得电磁波在传播过程中的相位发生显著变化。在相同位移的传播过程中，液面高度的变化会导致末端检测到相位差值的变化。

同轴线式传感器由内外两个圆导体组成，如图1所示。内导体半径为a，外导体内径为b，传感器有效总长为L。Z=l0和Z=l1处分别为液面变化前后的液面位置。左侧电磁波载体为空气，其主要参数为 ε0，μ0，σ0;右侧为溶液，其主要参数为 ε1，μ1，σ1。Z=0处为电磁波发射端，电磁波的角频率为ω，初始相位为φ0;Z=L处为电磁波接收端。

图1 同轴线式传感器Fig．1 Coaxial line sensor

当液面高度在z=l0位置时，在z=L处的电场强度可表示为式(4):

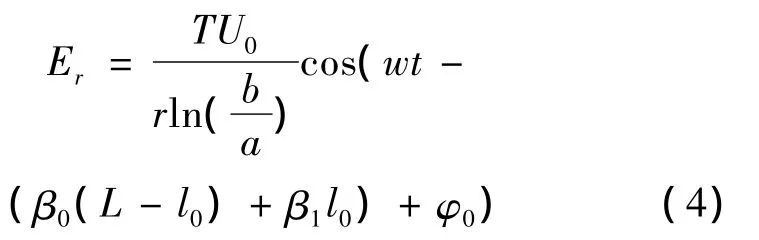
当液面高度变化Δl偏移至z=l1时，在z=L处的电场强度可表达为式(5):

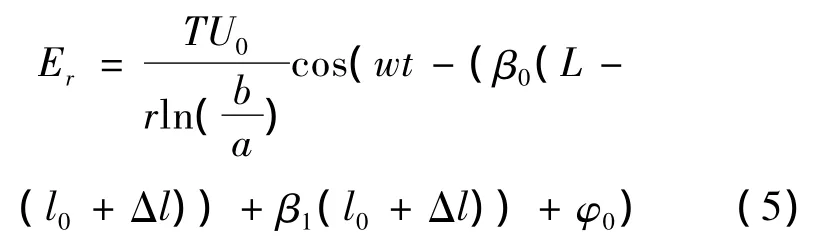
依据式(5)和式(6)，可以得到液位变化值与相位变化量的函数关系如式(6):

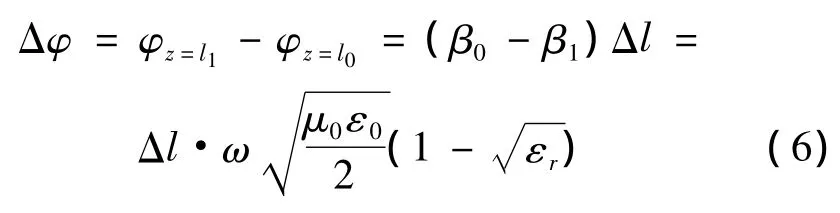
所以，当标定液位高度在z=l0时同轴线式传感器两端的相位差为Φ0，测量液面变化后的同轴线两端相位为Φ1，计算得到相位差值的变化量如式(7)，即可计算出当前液面的高度:

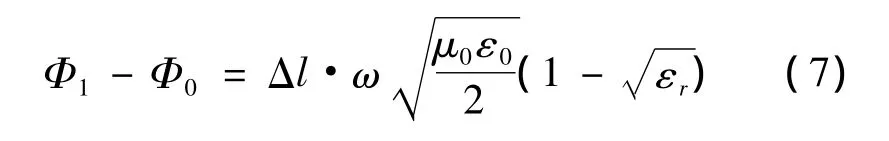
1．3 同轴线式传感器的尺寸选择

使用同轴线式传感器进行液位测量时，必须保证电磁波在传感器内的传播主模为TEM波，那么同轴线内最短的工作波长λmin与同轴线尺寸之间应该满足以下关系式:

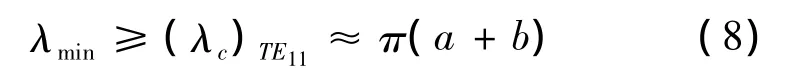
同时，为了避免相位检测带来的多解性，液位测量的有效高度在最短工作波长λmin内，即有下式:

最后，要求电磁波在传播过程中，需要保证电磁波在同轴线式传感器内的有效传播，所以在选择合适的传感器尺寸及电磁波发射频率和幅值后，对系统加以校验，以保证测量的可行性和可靠性。

2 同轴线式传感器仿真分析

HFSS应用切向矢量有限元法，可求解任意三维射频、微波器件的电磁场分布，计算由材料和辐射带来的损耗;其仿真分析可直接得到特性阻抗、传播系数、S参数及电磁场分布、天线方向图、特定吸收率等参数［7-9］。

同轴线式传感器模型主要由内导体、外导体、空气介质及柴油介质等组成。内外导体的材料选择为铜，不同材料的主要属性参数如表1所示。

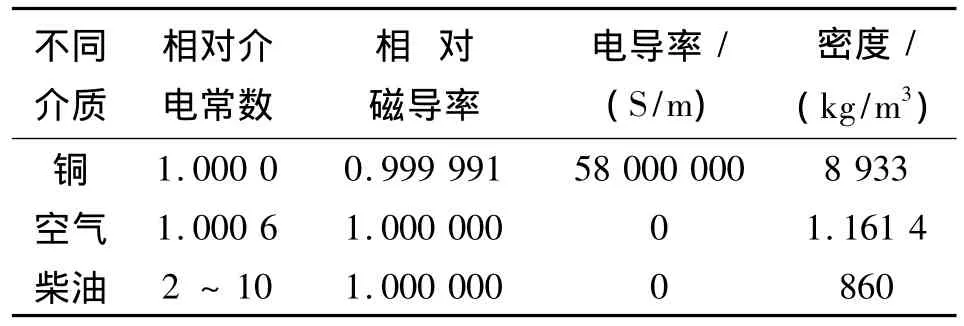
表1 材料主要属性参数Tab．1 Main property parameters about materials

设置内导体直接为2 mm，外导体直接为5 mm，总长度为50 mm，建模图形如图2所示。

2．1 电磁波频率对相位差值的影响

柴油的相对介电常数取2，同轴传感器内径为2 mm，外径为5 mm，仅仅改变电磁波的频率，电磁波的频率分别选择 75 MHz，150 MHz，250 MHz，300 MHz，500MHz，600MHz，750MHz，900MHz，1 GHz，1．5 GHz。上述10组模型的仿真结果如图3所示，其横坐标为5 mm的整数倍。

图2 同轴线式液位传感器建模Fig．2 Model of liquid level sensor using coaxial line

图3 改变电磁波参数的仿真结果Fig．3 Results of simulation by changing frequency of electromagnetic waves

电磁波频率从75 MHz调高到1 500 MHz，所有的采样频率上，同轴线传感器两端的相位差与柴油液面高度的变化成线性关系，电磁波的发射频率越高，同轴线传感器两端的相位差值越大，与推导的式(7)符合。

进一步处理可以得到每5 mm柴油液面高度变化引起相位差的变化量与电磁波频率的关系如图4所示。从图中可以看出，电磁波的频率越高，一定高度油液变化引起的相位差变化值也越大，同轴线传感器的精度要求更高。

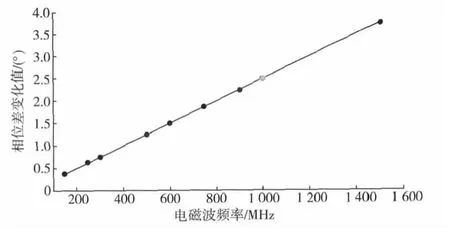
图4 频率与相位差变化值的关系Fig．4 Diagram about frequency and change of phase difference

2．2 相对介质常数对相位差值的影响

同轴线传感器的内径为2 mm，外径为5 mm，电磁波的频率取250 MHz，仅仅改变柴油的相对介电常数，柴油的相对介电常数分别取 2，3，4，5，6，7，8，9，10。上述9组模型的仿真结果如图5所示，其横坐标为5 mm的整数倍。

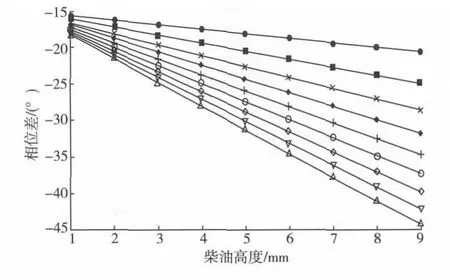
图5 改变柴油相对介电常数的仿真结果Fig．5 Results of simulation by changing diesel relative dielectric constant

当柴油的相对介电常数有2～10，每隔1的上升，同轴线传感器两端的相位差与柴油液面高度的变化成线性关系，柴油的相对介电常数越大，同轴线传感器两端的相位差值越大，与式(7)符合。

在采样的频率下，每5 mm柴油液面高度变化引起相位差的变化量与电磁波频率的关系如图6所示。从图中可以看出，柴油的相对介电常数越大，一定高度油液变化引起的相位差变化值也越大，同轴线式传感器的精度要求更高。

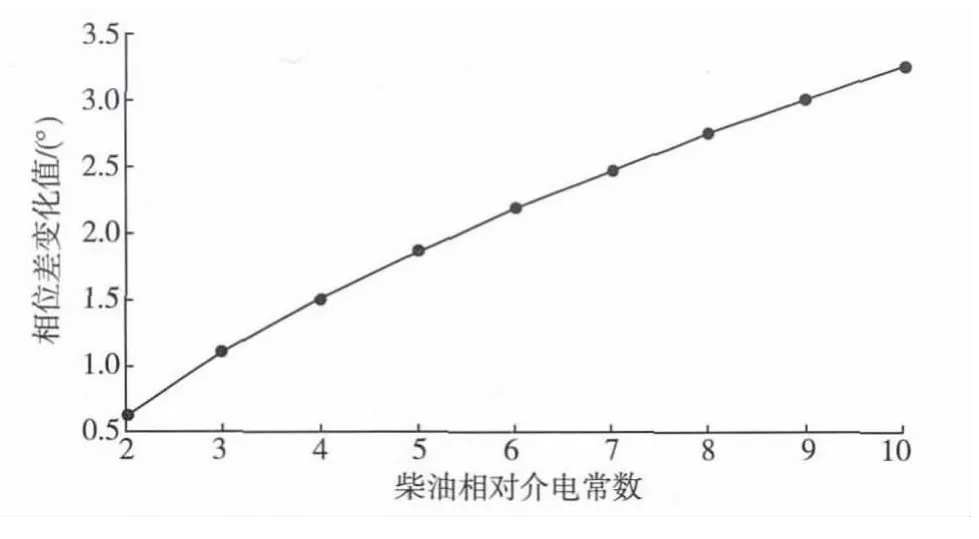
图6 柴油相对介电常数与相位差变化值的关系Fig．6 Diagram about diesel relative dielectric constant and change of phase difference

2．3 仿真结果分析

通过图3和图5可以发现，当同轴线式传感器的总长度为定值时，同轴线两端的相位差值与柴油液位的变化趋近于线性关系。同时电磁波频率越高，柴油的相对介电常数越大，定长同轴线式传感器两端的相位差值越大。

3 结语

根据同轴线内电磁波的传播理论，调整测量系统的各项参数，利用三维电磁场设计分析软件HFSS对同轴线式液位传感器进行建模仿真，得到了不同模型下的相位变化计算结果。仿真结果与理论计算值较为符合，验证了理论的正确性和利用同轴线式传感器测量液面高度的可行性

［1］刘翠玲，李亮亮，王进旗．同轴相位法井下原油含水率温度特性的实验研究［J］．仪表技术与传感器，2012(3):82-84．LIU Cuiling，LI Liangliang，WANG Jinqi．Experimental research on temperature influence on measurement of water content in crude oil based on coaxial phase method［J］．Instrument Technique and Sensor，2012(3):82-84．(in Chinese)

［2］王进旗，强锡富，张勇奎．同轴线式相位法测量油井含水率［J］．仪器仪表学报，2002，23(1):74-76．WANG Jinqi，ZHANG Xifu，ZHANG Yongkui．Coaxial transimission line phase method for oil well［J］．Chinese Journal of Scientific Instrument，2002，23(1):74-76．(in Chinese)

［3］David V Blackham，Roger D Pollard．An improved technique for permittivity measurements using a coaxial probe［J］．IEEE Transactions on Instrumentation and Measurement，1997，46(5):1093-1099

［4］葛德彪，魏兵．电磁波理论［M］．北京:科学出版社，2011．

［5］张厚等．电磁场与电磁波及其应用［M］．西安:西安电子科技大学出版社，2012．

［6］王文祥．微波工程技术［M］．北京:国防工业出版社，2014．

［7］潘雪，张昕，杨晓东，等．基于HFSS泄漏电缆辐射特性仿真分析［J］．哈尔滨商业大学学报:自然科学版，2013，29(4):448-451．PAN Xue，ZHANG Xin，YANG Xiaodong，et al．Research on radiation characteristics of leaky coaxial cable using HFSS［J］．Journal of Harbin University of Commerce:Natural Sciences Edition，2013，29(4):448-451．(in Chinese)

［8］陈利祥，初蕾，张宁，等．微波烧结腔内电场的HFSS仿真与实测分析［J］．青岛大学学报:自然科学版，2011，24(1):33-37．CHENG Lixiang，CHU Lei，ZHANG Ning，et al．HFSS simulation of electromagnetic in single mode cavity for microwave sintering［J］．Journal of Qingdao University:Natural Science Edition，2011，24(1):33-37．(in Chinese)

［9］李明洋，刘敏．HFSS电磁仿真入门到精通［M］．北京:人民邮电出版社，2013．