关于平方型Altman映象的公共不动点定理

张树义， 赵美娜， 李 丹

(渤海大学数理学院，辽宁 锦州121013)

1 引言与预备知识

Altman型映象不动点存在性的研究，始于1975年。Altman证明了完备度量空间(X，d)中一个映象S不动点的存在性:

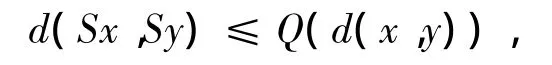
其中∀x，y∈X，Q为从［0，+∞)到自身的递增函数且满足:

Ⅰ)0 ＜Q(t)＜t，t∈(0，+∞);

Ⅱ)函数p(t)=t/(t－Q(t))递减;

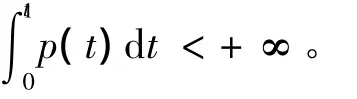
此后，Altman型映象的不动点定理有了进一步的改进和推广。在Altman型映象不动点问题的研究中，已往的都是讨论不带平方Altman型映象不动点的存在性［1-7］。最近，栾丹等［8］讨论了一类平方型Altman映象公共不动点的存在性。

文中在此基础上建立一类新的更广泛的平方型Altman映象公共不动点定理，所得结果改进和推广了文献［8］中的结果。张树义等［9］给出了一类Φ-压缩映象公共不动点的存在性。文献［10-16］利用不动点定理，讨论了起源于动态规划的几类泛函方程组解的存在性和唯一性。受此启发，作为应用文中还讨论了一类泛函方程组解的存在与唯一性。

文中设S，A，T，B是X上的4个自映象，Z+为非负整数集。

注1 由条件Ⅰ)及Q的递增性可知:Q(0)=0且Q(t)=t⇔t=0。

2 主要结果

［1］Altman M．A fixed point theorem in compact metric spaces［J］．Amer Math Monthly，1975，82(8):827-829．

［2］Garbone A，Singh S P．Common fixed point theorem for Altman type mappings［J］．Indian J Pure Appl Math，1987，18(12):1082-1087．

［3］刘泽庆．关于Altman型映象的公共不动点定理［J］．辽宁师范大学学报:自然科学版，1993，16(1):1-4．LIU Zeqing．On common fixed points of Altman type mappings［J］．Journal of Liaoning Normal University:Natural Science Edition，1993，16(1):1-4．(in Chinese)

［4］张树义．Altman型映象的公共不动点定理［J］．烟台师范学院学报:自然科学版，2000，16(2):95-97．ZHANG Shuyi．Common fixed point theorem of Altman type mappings［J］．Journal of Yantai Normal University:Natural Science Edition，2000，16(2):95-97．(in Chinese)

［5］谷峰，邓波．关于Altman型映象的公共不动点［J］．哈尔滨师范大学学报:自然科学版，2001，17(5):44-46．GU Feng，DENG Bo．Common fixed point for Altman type mappings［J］．Journal of Harbin Normal University::Natural Science Edition，2001，17(5):44-46．(in Chinese)

［6］董清平，谷峰．广义拟弱交换映象的公共不动点定理［J］．杭州师范大学学报:自然科学版，2008，7(1):21-23．DONG Qingping，GU Feng．Common fixed point theorems for generalized quasi weak commutativity mapping［J］．Journal of Hangzhou Normal University:Natural Science Edition，2008，7(1):21-23．(in Chinese)

［7］张树义，衣立红，邵颖．Altman型映象的公共不动点［J］．杭州师范大学学报:自然科学版，2008，7(6):401-404．ZHANG Shuyi，YI Lihong，SHAO Ying．Common fixed point for Altman type mappings［J］．Journal of Hangzhou Normal University:Natural Science Edition，2008，7(6):401-404．(in Chinese)

［8］栾丹，宋晓光．一类平方型Altman映象的公共不动点定理［J］．渤海大学学报:自然科学版，2014，35(2):111-113．LUAN Dan，SONG Xiaoguang．Common fixed point for a class of twice power type Altman mapping［J］．Journal of Bohai University:Natural Science Edition，2014，35(2):111-113．(in Chinese)

［9］张树义，宋晓光．Φ-压缩映象的公共不动点定理［J］．北华大学学报:自然科学版，2014，15(2):167-173．ZHANG Shuyi，SONG Xiaoguang．Common fixed point for Φ-contraction mapping［J］．Journal of Beihua University:Natural Science Edition，2014，15(2):167-173．(in Chinese)

［10］HUANG N J，Lee B S，KANG M K．Fixed point theorems for compatible mappings with applications to the solutions of functional equations arising in dynamic programmings［J］．Int J Math and Math Sci，1997，20(4):673-680．

［11］LIU Z Q，GUO Z Y，KANG S M，et al．A fixed point theorem and its application in dynamic programming［J］．Int J App Math Sci，2006，3(1):11-19．

［12］Navshinde S，Achari J．Common fixed point of commuting mappings with application to dynamic programming［J］．Int J Contemp Math Sci，2010，5(43):2111-2121．

［13］CAI T，CHEN L，LIU Z Q，et al．A common fixed point theorem fot two pairs of compatible mappings and its applications［J］．Int J Pure and App Math，2008，44(3):385-397．

［14］LIU Z Q．Compatible mappings and fixed points［J］．Acta Sci Math，1999，65:371-383．

［15］WEI Li，KANG S M．A common fixed point theorem fot compatible mappings with application to functional equations arising in dynamic programming［J］．Fixed Point Theory and Applictions，2003(5):155-161．

［16］Pathak H K，CHO Y J，KANG S M，et al．Fixed point theorems for compatible mappings of type(P)and applications to dynamic programming［J］．Le Matematiche，1995，50(1):15-33．

［17］Jungck G．Compatible mappings and common fixed points［J］．Internat J math and Math Sci，1986，9(4):771-779．

［18］刘立山．(次)相容映象公共不动点定理与广义Ishikawa迭代逼近定理［J］．曲阜师范大学学报:自然科学版，1990，16(2):40-44．LIU Lishan．Common fixed points theorems of(sub)compatible mappings and generalized Ishikawa iterative approximation theorems［J］．Journal of Qufu Normal University:Natural Science Edition，1990，16(2):40-44．(in Chinese)