基于Copula-GARCH-M的开放式基金投资组合风险分析

曹文彬， 施丽云， 胡培玲

(江南大学商学院，江苏 无锡214122)

开放式基金是一种风险共担、惠益共享的集合投资工具。开放式基金虽然具有分散风险、专业理财的作用，但它无法规避市场风险、流动性风险和其他风险。我国开放式基金相对于世界其他国家而言起步较晚，发展不完善，但随着我国经济的发展，基金业规模迅速扩大。到目前为止，基金的总份额为48 316．53亿元，从绝对金额来看仍处于世界第三阶梯。基金业发展不仅需要以国民经济发展为基础，而且还需要以金融市场尤其是股票市场为依托。

开放式基金净值受股票和债券价格波动的影响，因此股票和债券价格的波动将对开放式基金投资带来严重的市场风险。因为金融市场中资产收益具有非正态、非对称和厚尾的特点，所以参照传统理论对风险进行计算一定会存在误差。对于投资者而言，高收益、低风险的基金是最佳选择，因此如何更加有效地衡量开放式基金的风险成为风险管理的关键。

目前VaR方法是在金融实务界使用最广泛的风险管理方法，VaR值在表示风险大小时简明直观。VaR是指在一定持有期内，在给定的概率置信水平下，某一金融资产所面临的潜在的最大损失。按照传统方法计算投资组合VaR值，均以金融资产收益线性相关且服从正态分布为前提，但实际上金融资产的收益往往呈现出“尖峰厚尾”的特征，同时又存在非线性相依结构，因此在假设与实际不符的情况下，计算出的投资组合风险值存在一定的误差。于是在投资组合风险研究中必须引入新的理论。1959 年Sklar提出了Copula函数［1］，该函数不仅可以有效、全面地捕捉多个序列之间的非线性结构，还可以将边缘分布和相依性分开研究;同时不要求具有同样分布形式的边缘分布，消除了对边缘分布和联合分布正态性假设的依赖。但当时并未将其理论引入到金融领域，只是用于简单描述多个随机变量之间的非线性相依结构。直到1999年Copula理论才被Embrechs引入到金融领域［2］，进而把金融风险分析推向一个新的台阶。

2002年张尧庭［3］将Copula引入国内金融风险研究中。2003年韦艳华等［4］探讨了Copula在金融领域的应用。Copula函数弥补传统技术的不足，用以刻画变量之间的相依性，如童中文、何建敏［5］、刘琼芳［6］、Anne-Laure Delatte［7］陆续用 Copula 模型对不同的相依性进行研究。而且Copula函数是将多个一元分布连接起来构成联合分布的连接函数，在估算风险值时，一维边缘分布函数的准确刻画也是至关重要的［8］。因为投资组合风险值大小的估算直接受一维边缘分布函数对单项金融资产刻画精确程度的影响，所以单个金融资产收益的描述成为众多学者关注的焦点。金融资产收益具有波动长记忆性、持续性及尖峰厚尾等特征，现阶段GARCH族模型是用以刻画金融时间序列最常用的波动模型。吴振翔等［9］在研究Copula和GARCH两个函数优势的基础上，建立了新的投资组合风险分析模型(即Copula-GARCH模型)，利用该模型对我国股票市场投资组合问题进行更精准地风险分析;Fangxia Lin［10］用Copula-AR-GARCH模型研究股票指数收益率和外汇收益率的尾部相关性;Jaghoubi Salma［11］又以Copula-GARCH模型研究了外汇市场和股票市场的相依结构;刘桂梅等［12］用其研究和分析金融股及上证地产股指数的收益率相关性问题。

尽管GARCH模型能够有效地刻画投资组合中单个金融资产收益边缘分布，但对于单个金融资产收益与风险关系的描述却显得无能为力。资产组合的风险不仅与投资组合的风险息息相关，还与单一资产的风险密切相关。Copula函数能够有效地刻画投资组合的风险，但单个资产的风险则需要由边缘分布表示，因此需要新的工具更好地刻画单个金融资产收益的边缘分布。GARCH-M模型中的均值等式里加入了与风险具有相同量纲的条件方差［13-15］，能够有效衡量单个金融资产收益和风险之间的关系。所以在研究投资组合风险时，若将GARCH-M模型与 Copula理论联合起来，建立一个新的Copula-GARCH-M模型，不仅可以描述单个金融资产的收益分布，而且能够有效刻画投资组合的相依性，确保风险估计更加精准。

针对投资组合风险管理，文中采用GARCH-M模型以刻画金融资产收益的边缘分布，结合描述金融资产间相依结构的 Copula函数，建立Copula-GARCH-M模型研究和分析投资组合风险。最后利用蒙特卡洛对投资组合的VaR值进行模拟估计，实例分析该模型对投资风险度量是否有效。

1 基于Copula-GARCH-M的风险计算

文中在利用Copula函数对多维资产投资收益与风险正确估算的前提下，对资产组合中单个金融资产收益分布进行估计。基于单个金融资产投资收益与风险之间的关系，需要先采用CARCH-M模型刻画投资组合中的边缘分布，然后与Copula函数进行组合得出联合分布Copula-GARCH-M模型，最后采用蒙特卡洛对VaR值模拟估计。

1．1 GARCH-M 模型

投资组合的风险采用联合分布Copula函数度量时，每项资产收益率的边缘分布首先要确认。大量研究表明，金融资产收益具有自相关性和异方差性。由于GARCH族模型预测的是被解释变量的方差，资产收益自相关性和异方差性的影响可以用该模型消除。

假设投资组合中有 n个金融资产，采用GARCH(1，1)模型对资产i(i=1，2，…n)的近T期历史数据yt(t=1，2，…T)进行建模，具体如下:

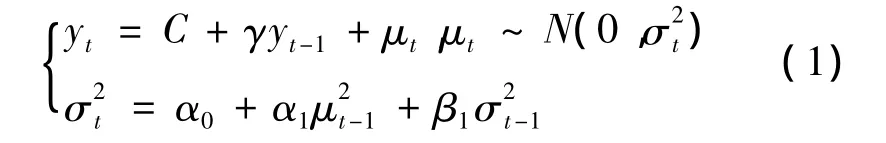
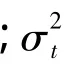
假设投资组合中有 n个金融资产，采用GARCH(1，1)-M模型对资产i(i=1，2，…n)的近T期历史数据 yt(t=1，2，…T)进行建模，具体如下:

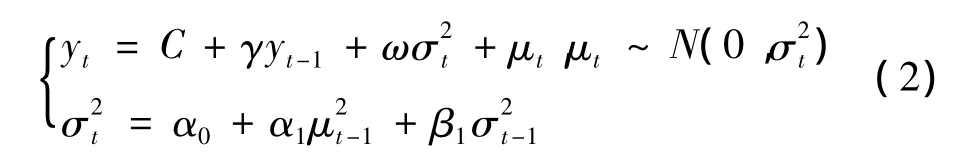
其中:yt为金融资产收益率;σ2t为收益率的条件异方差;随机扰动项 μt服从正态分布 N(0，σ2t);α0，α1，β1为待估计的参数。在均值等式中，加入条件方差因素，收益率与风险之间的关系通过其系数ω衡量。如果ω＞0，则表示该金融资产的风险与收益率成正比;如果ω＜0，则表示资产风险与收益率成反比。

1．2 计算Copula-GARCH-M联合分布函数

假设金融资产组合中存在n个资产，已有样本收益r=(rt1，rt2，…，rtn)t=1，2，…，T，依据式(2)对GARCH-M模型中参数的估计，每项资产收益率的边缘分布Fi(ri)i=1，2，…，n基本可以确定。由于每种资产的收益和风险的关系是不同的，而且资产之间具有非线性相关。当投资比例一定时，可以采用Copula联合分布函数描述其间的相依结构。

多个金融资产的相关关系可以通过阿基米德Copula函数和椭圆Copula函数描述。文中采用椭圆Copula函数，其中椭圆Copula函数包括正态Copula函数和t-Copula函数。

n元正态Copula函数表达式

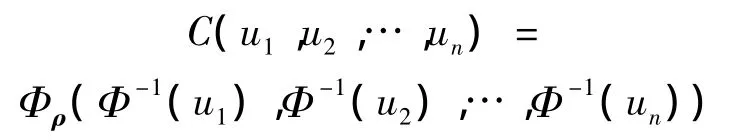
式中:ρ为n元正态分布中的相关系数矩阵;Φρ为相关系数为ρ的多元正态分布函数;Φ－1为一元标准正态分布函数的反函数。

令u1=F1(r1)u2=F2(r2)，…，un=Fn(rn)，计算出正态Copula下的相关系数矩阵ρ，并将其带入式(1)可中得到正态copula的估计。

n元t-Copula函数表达式

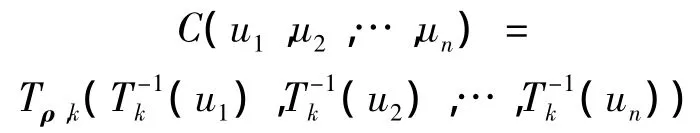
令 u1=F1(r1)，u2=F2(r2)，…，un=Fn(rn)，计算出t-Copula下的相关系数矩阵ρ和自由度k，并将其带入式(2)可中得到t-Copula的估计。

1．3 利用蒙特卡洛模拟VaR值

在实际应用中，一定置信水平下的金融资产损失或超额平均损失通常采用VaR描述。目前，VaR有3种不同的计算方法:方差-协方差法、历史模拟法、蒙特卡洛模拟法。由于投资组合的VaR解析式在Copula-GARCH-M模型中不易求出，因此文中采用蒙特卡洛仿真计算。蒙特卡洛仿真是利用原始数据市场因子和资产价值的映射反复模拟，得出多个资产价值。最终通过模拟得到的分布情况，估算出一定置信水平下的VaR值。

1．3．1 正态Copula-GARCH-M模型

1)把相关系数ρ进行Cholesky分解，ρ=AAT。

2)产生n个独立同分布的随机向量

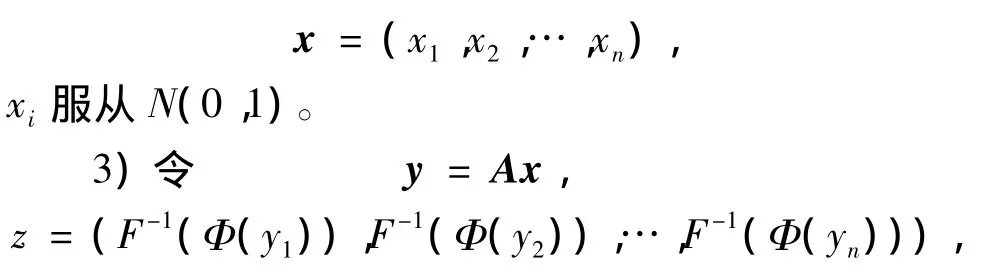
其中，F－1为单个金融资产的边缘分布函数的反函数;Φ为一元标准正态分布函数。

4)假定投资组合中资产的权重

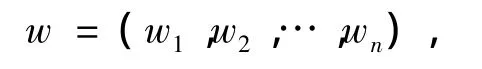
可计算出投资组合的收益值Z=wz'。

5)投资组合未来收益的1 000种模拟情形，可以通过重复以上2)～4)1 000次得到;投资组合损失的经验分布通过模拟的情景集得到。在置信度为1－α的情况下，由P(V≤VaR)=α求出其投资组合VaR值。

1．3．2 t-Copula-GARCH-M 模型

1)把相关系数ρ进行Cholesky分解，ρ=AAT。

2)产生n个独立同分布的随机向量

3)令y=Ax，再产生一个与x独立、自由度为k的卡方分布随机变量S，令

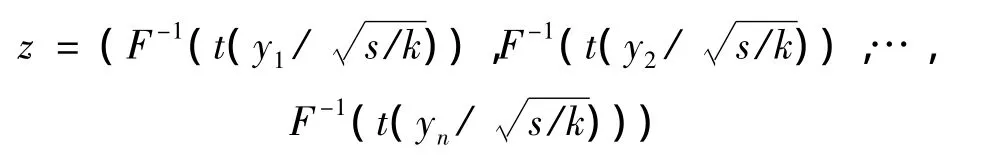
其中，F－1为单个金融资产的边缘分布函数的反函数;t为一元标准t分布函数。

4)假定投资组合中资产的权重 w=(w1，w2，…，wn)，可计算出投资组合的收益值Z=wz'。

5)投资组合未来收益的1 000种模拟情形，可以通过重复2)、3)、4)1 000次得到，投资组合损失的经验分布通过模拟的情景集得到。在置信度1－α的情况下，由P(V≤VaR)=α求出其投资组合VaR值。

2 实证分析

2．1 数据的选取与处理

文中在研究华夏沪深300交易型开放式指数证券投资基金2013年年度报告的基础上，优先选取华夏沪深300基金中具有代表性的前10名股票为考察对象。即中国平安(601318)、招商银行(600036)、民生银行(600016)、海通证券(600837)、兴业银行(601166)、浦发银行(600000)、格力电器(000651)、万科A(000002)、农业银行(601288)、交通银行(601328)等10支股票。2013年样本股票所占基金资产净值比例见表1。以此10支股票2010年9月2日至2014年3月25日785个交易日的收盘价(去除10支股票中任何一支股票不开盘的交易日)为原始数据。这些股票的日收益率是通过上述收盘价为基础计算得出的，

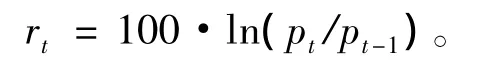
其中，rt为日对数收益率;pt为每日收盘价。通过对数据的基本信息进行统计分析，得到10支股票收益率的描述性统计(见表2)。

由表2可以看出，在样本观察期内，投资组合收益率10支股票中有正有负。就偏度而言，左偏是中国平安、兴业银行、交通银行这3支股票的收益率，其中兴业银行的偏度统计值大于3，这意味着兴业银行的收益存在着巨幅下跌的可能;对于偏度为正值的剩余7支股票而言，它们的收益率为呈现右偏的现象。从峰度观察，10支股票的峰度值均大于4，说明10支股票的收益率都存在着厚尾的尾部特征。由J-B检验统计量可知，各支股票的J-B检验值远远大于临界值，说明投资组合中各支股票的收益率均不服从正态分布。

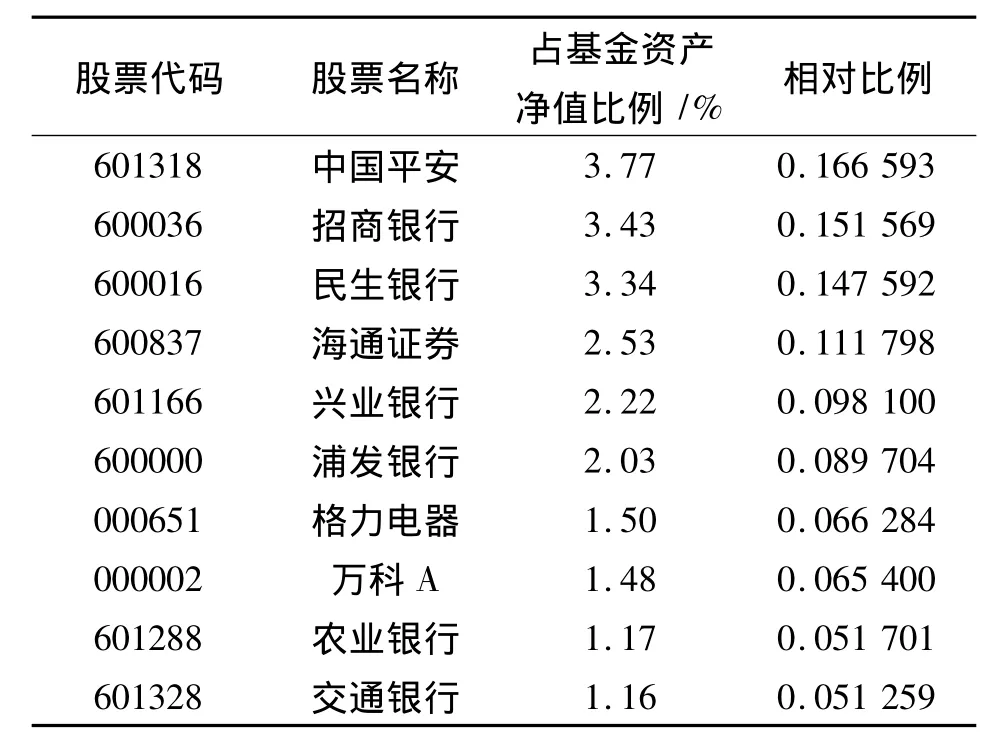
表1 2013年华夏沪深300基金Top 10股票Tab．1 Top 10 stock of the 2013 Huaxia csi 300 fund

表2 股票收益序列的基本统计性质Tab．2 Basic statistical properties of the stock returns series

2．2 边缘分布模型的参数估计

利用Eviews软件得出中国平安收益率的自相关、偏相关系数，结果见表3。由表3可以看出，Q统计量的收尾概率在各期都不为0，表明在1%的显著水平下，不拒绝原假设“不存在自相关性”，即样本数据不存在相关性。当运用ARCH-LM方法检验序列的条件异方差性时，其检验统计量LM值为20，给定显著水平0．01 时 χ2为18．48，LM ＞ χ2，说明收益的误差序列存在条件异方差，因此股票收益率序列可以通过GARCH族模型描述。同理，可检验出其他9支股票收益率同样存在着条件异方差。文中选取GARCH(1，1)-M模型对投资组合的边缘分布进行描述。将数据代入模型，模型中的估计参数可用Eviews求出(见表4)。

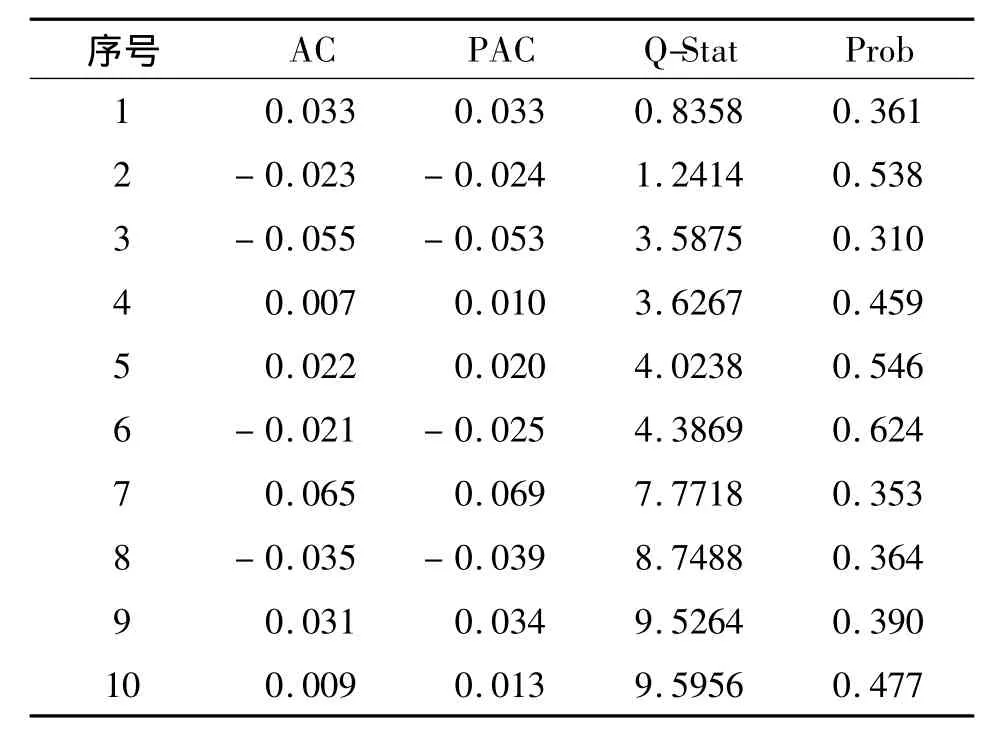
表3 中国平安收益率的自相关、偏相关系数表Tab．3 Autocorrelation and partial correlation coefficients of the Ping An's yields

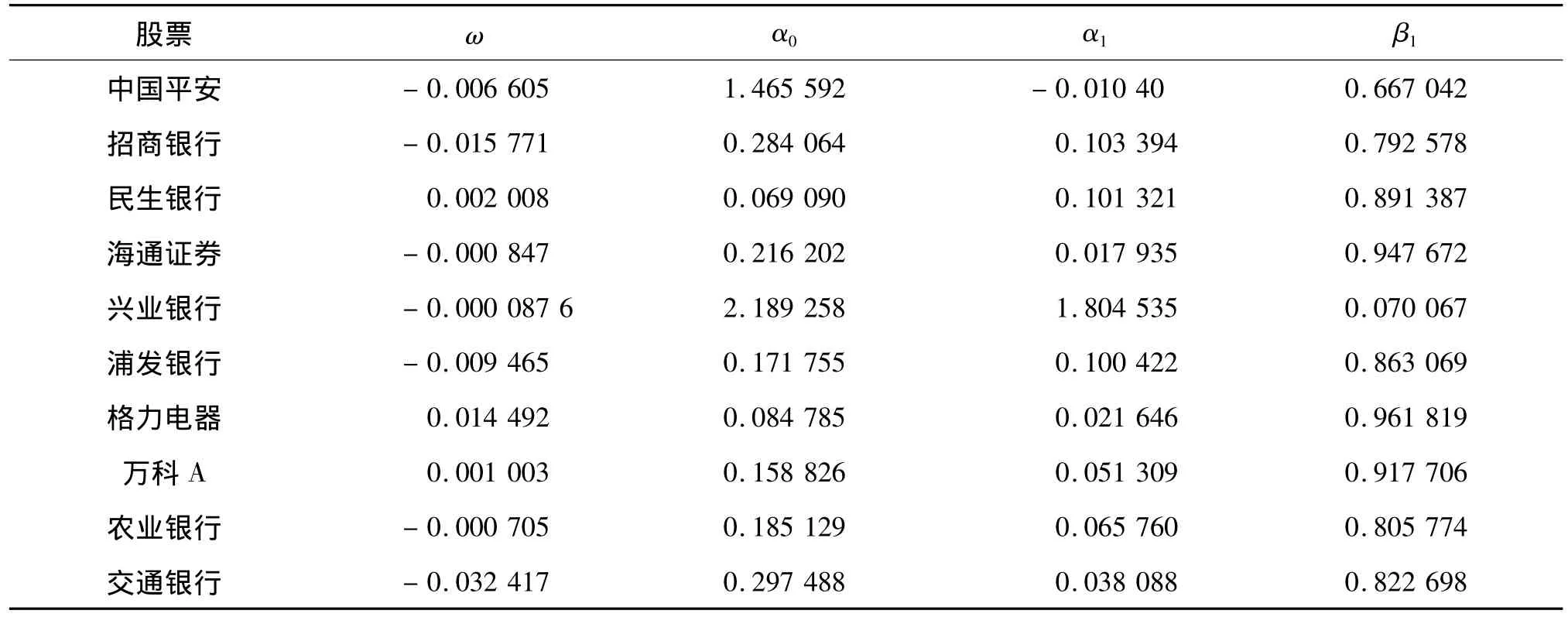
表4 GARCH(1，1)-M模型的参数估计Tab．4 Estimatse of the parameters in the GARCH(1，1)-M Model

由表4可以看出，当各支股票的边缘分布利用GARCH(1，1)-M 模型描述时，GARCH(1，1)-M 模型的均值等式中加入了与风险等量纲的条件方差，明显可以从等式系数中看出风险与收益的关系。在正常情况下，投资的收益与风险一般都是呈现出正相关性，即收益随着的风险的增加而增加;但是在这10支股票中，有7支股票收益率的方程等式风险系数为负值，即风险越小，收益越大。说明投资该基金组合中某些单个支股票的风险与收益成反比。

以中国平安为例，通过对原收益率序列进行概率积分转换，从而得到如图1所示的服从(0，1)均匀分布的新数列。

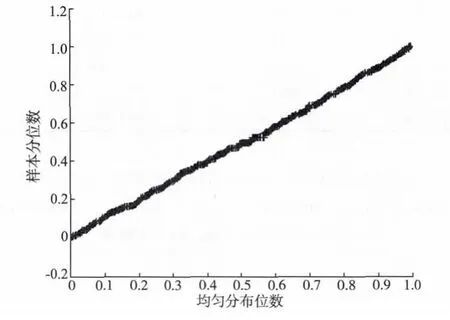
图1 Q-Q图检验中国平安收益率分布数列Fig．1 Q-Q diagram test yields distribution

由图1可以看出，新序列能够较好地拟合(0，1)上的均匀分布，故可对变化后的新序列进行Copula函数模拟。利用此方法检验剩余9支股票发现，它们的收益率进行概率积分转换后同样能够较好的拟合(0，1)上的均匀分布。

2．3 Copula-GARCH-M模型的参数估计

依据上一步得到的各样本收益序列的边缘分布，与正态Copula函数和t-Copula函数分别联合起来，可以估量得到正态Copula函数与t-Copula函数的相关系数矩阵。根据GARCH(1，1)-M的边缘分布联合正态Copula函数和t-Copula函数估计得到如图2所示的相关系数矩阵。

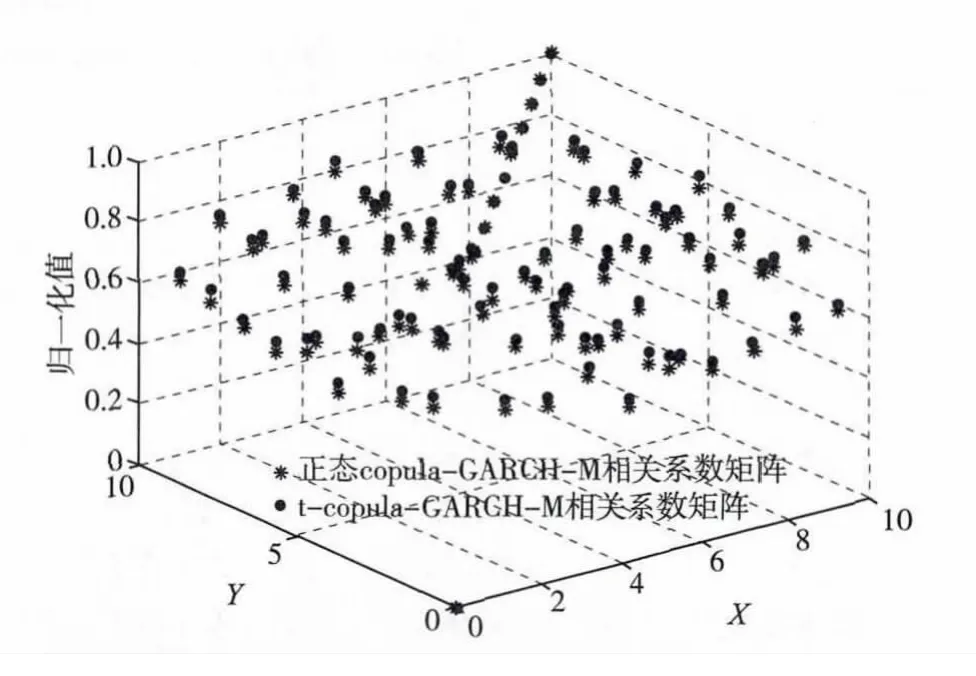
图2 正态Copula-GARCH-M和t-Copula-GARCH-M函数的相关系数矩阵的估计Fig．2 Estimates of correlation matrix in normal Copula-GARCH-M and t-Copula-GARCH-M

由图2可以看出，各支股票的相关性通过t-Copula-GARCH-M模型比正态Copula-GARCH-M模型更能直观的体现出来。

2．4 VaR 值计算

根据表1中各股票的投资比例，假设资产持有期的置信度为(0．01，0．05，0．1)，通过估计得到的Copula-GARCH(1，1)-M模型，使用蒙特卡洛模拟技术，模拟1 000次，模拟投资组合中每支股票的收益率序列，从而计算得出10支股票的损失序列。在置信度给定的前提下，持有期内相应的投资组合的VaR值可以通过得到的投资组合损失经验分布得出(见表5)。

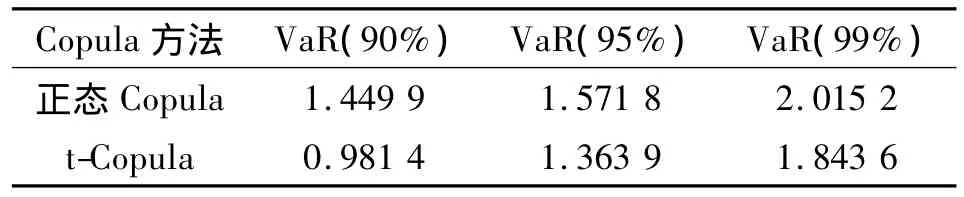
表5 正态Copula-GARCH-M和t-Copula-GARCH-M模型下的VaR值估计Tab．5 VaR values under normal Copula-GARCH-M and t-Copula-GARCH-M model

由表5可以看出，t-Copula方法下计算得到的VaR值比正态Copula方法下得到的值小。这是因为通过t-Copula函数比正态Copula函数能更好地反映出这10支股票间的尾部相依性。另外，组合中各支股票极端事件相互抵消的概率随着尾部相依程度的提高会大幅度提高，从而大大的降低了组合的风险。同时由表5可以看出，投资组合的风险可以通过t-Copula-GARCH-M模型进行有效度量。同样以沪深300开放式基金的前10名股票作为投资组合的样本， 对投资组合的 VaR值采用t-Copula-GARCH模型进行度量，通过比较对t-Copula-GARCH-M模型的精度进行进一步检验，具体结果见表6。

表6 t-Copula-GARCH和t-Copula-GARCH-M模型的VaR值Tab．6 VaR value of the t-Copula-GARCH and the t-Copula-GARCH-M model

由表6可以看出，在不同置信水平下，t-Copula-GARCH-M模型下计算出的VaR都比t-Copula-GARCH模型估计得到的VaR值小，说明投资组合风险的计算精度相对较高的模型是t-Copula-GARCH-M模型。因为，在GARCH-M模型将条件方差引入到均值方程中，使得收益与风险联系在一起，与GARCH模型相比，GARCH-M模型刻画金融金融资产的波动性的具有更高的拟合度。在波动性拟合优度更高的基础上，结合t-Copula模型描述开放式基金投资组合联合分布情况，从而估计出的VaR值更为精确，效果更好，参考价值越高。

3 结语

资产组合的风险即包括投资组合的风险也包括单一资产的风险，两种风险分别由投资组合相依性和单个资产收益分布描述。考虑到单个金融资产收益的非对称和厚尾性、资产收益与风险的关系以及投资组合资产间的非线性关系，单个资产收益的分布可以通过采用GARCH-M模型描述，同时结合描述多个金融资产之间相依结构的t-Copula联合分布函数，运用蒙特卡洛模拟估计投资组合风险VaR值。从对沪深300基金风险的实证结果可以得出以下结论:当投资总额一定时，投资组合风险降低的程度与置信度成正比;通过与t-Copula-GARCH模型对比发现，t-Copula-GARCH-M模型度量风险的能力更强。通过采用GARCH-M模型来刻画投资组合中单个资产边缘分布的实证表明，该模型不仅能够很好的反映金融资产与风险的关系，而且能更加有效的刻画资产收益的尖峰厚尾的特征，因此可以将GARCH-M模型作为刻画投资组合边缘分布的强有力的工具。

同时必须指出，文中是运用静态Copula函数刻画各支股票的收益率，没有考虑时变的因素。动态Copula函数能够描述组合中各资产收益随时间变化而产生不同关联程度的变动，反映在当时政策或外在金融事件对投资组合中各股票收益关联程度的影响下，收益的实际变动情况，而静态copula函数却无法及时反应外在环境的变化。在今后可以以动态Copula函数作为重点进行研究。

［1］Sklar A．Fonctions de répartition à n dimensions et leurs marges［J］．Publ Inst Statist Univ Paris，1959(8):229-231．

［2］Embrechts P，McNeil A，Straumann D．Correlation:pitfalls and alternative［J］．Risk-Lond on Risk Magazine Limited，1999，12:69-71．

［3］张尧庭．连接函数(Copula)技术与金融风险分析［J］．统计研究，2002(4):48-51．ZHANG Yaoting．Copula technique and financial risk analysis［J］．Statistical Research，2002(4):48-51．(in Chinese)

［4］韦艳华，张世英，孟利锋．Copula理论在金融上的应用［J］．西北农林科技大学学报，2003，3(5):97-101．WEI Yanhua，ZHANG Shiying，MENG Lifeng．Copula theory and its application in finance［J］．Journal o f Northwest Sci-Tech University of Agriculture and Forestry，2003，3(5):97-101．(in Chinese)

［5］童中文，何建敏．基于Copula风险中性校准的违约相关性研究［J］．中国管理科学，2008，16(5):22-27．TONG Zhongwen，HE Jianmin．Study on the default correlation based on risk neural copula［J］．Chinese Journal of Management Science，2008，16(5):22-27．(in Chinese)

［6］刘琼芳，张宗义．基于Copula房地产与金融行业的股票相关性研究［J］．管理工程学报，2011(1):165-170．LIU Qiongfang，ZHANG Zongyi．Investigating the dependence structure between real estate and finance industries based on the copula function［J］．Journal of Industrial Engineering and Engineering Management，2011(1):165-170．(in Chinese)

［7］Anne-Laure Delatte，Claude Lopez．Commodity and equity markets:some stylized facts from a copula approach［J］．Journal of Banking and Finance，2013，37(12):5346-5356．

［8］周孝华，张保帅，董耀武．基于Copula-SV-GPD模型的投资组合风险度量［J］．管理科学学报，2012，15(12):70-78．ZHOU Xiaohua，ZHANG Baoshuai，DONG Yaowu．Risk measurement of financial portfolio based on Copula-SV-GPD model［J］．Journal of Management Sciences in China，2012，15(12):70-78．(in Chinese)

［9］吴振翔，陈敏，叶五一，等．基于Copula-GARCH的投资组合风险分析［J］．系统工程理论与实践，2006(3):45-52．WU Zhenxiang，CHEN Min，YE Wuyi，et al．Risk analysis of portfolio by copula-GARCH［J］．System Engineering-Theory and Practice，2006(3):45-52．(in Chinese)

［10］LIN Fangxia．Tail dependence between stock index returns and foreign exchange rate returns-a copula approach［EB/OL］．(2011-07-01)［2015-02 －03］．http://dx．doi．org/10．2139/ssm．1931726．

［11］Salma Jaghoubi，Adel Boubaker．Greek crisis，stock market volatility and exchange rates in the european monetary union:a VARGARCH-Copula model［EB/OL］．(2012-09-01)［2015-01 －16］．http://dx．doi．org/10．2139/sm．2140086．

［12］刘桂梅，赵丽．基于Copula-GARCH模型的上证地产股和金融股的相关性研究［J］．浙江大学学报:理学版，2013，40(2):140-145．LIU Guimei，ZHAO Li．Research on the dependence of shanghai real estate shares index and financial index based on Copula-GARCH model［J］．Journal of Zhejiang Uinversity:Science Edition，2013，40(2):140-145．(in Chinese)

［13］John Elder．An impulse-response function for a vector autoregression with multivariate GARCH-in-mean［J］．Economics Letters，2003(79):21-26．

［14］田华，曹家和．中国股票市场报酬与波动的GARCH-M模型［J］．系统工程理论与实践，2003(8):81-86．TIAN Hua，CAO Jiahe．Some studies of the volatility and stock return o n China stock markets using GARCH-M［J］．System Engineering Theory and Practice，2003(8):81-86．(in Chinese)

［15］John Beirne，Guglielmo Maria Caporale，Marianne Schulze-Ghattas，et al．Global and regional spillovers in emerging stock markets:a multivariate GARCH-in-mean analysis［J］．Emerging Markets Review，2010(11):250-260．