基于广义遗传算法的路基沉降预测方法应用

卞志兵， 高正夏， 杨爱婷， 宗文亮

(河海大学地球科学与工程学院，江苏南京210098)

路基的最终沉降变形对于确定铺筑路面时间、控制和安排施工进度以及路堤的安全与正常使用至关重要。若过早铺筑路面，可能会导致路面出现断裂，路基路面结构出现沉陷，路表面出现波浪或车辙，使路况恶化、服务水平下降。而路基沉降计算的数值方法受填土材料、荷载大小、加载方式、几何尺寸等众多不确定因素的影响，计算结果往往较监测数值偏差很大。而且由于很多计算参数一般需要通过三轴试验确定，因而目前主要用于重要工程、重要地段计算。相比较而言，通过观测数据进行处理来预测沉降则是一种更简便快捷的方法。

针对路基沉降在时序上表现出的复杂的非线形特征，文中采用了处理复杂优化问题理想的遗传算法来确定模型参数。

1 广义遗传算法基本原理

1．1 基本原理及函数模型

遗传算法(Genetic Algorithms，GA)［1］是基于生物进化的仿生学算法中的一种，它建立于达尔文生物进化的“物竟天择，适者生存”的基本原理之上，是一种迭代自适应概率性优化搜索方法［2］。其基本思想由美国Holland教授等提出，现已成为多个交叉学科中一个热门的话题。普通GA的搜索方法结合了达尔文适者生存及随机信息交换的思想，前者消除了解中的不适定因素，后者则利用了原有解中的知识，从而加快了搜索过程。由于普通的简单遗传算法变异操作发生的概率很低，使它很难从局部最优中跳出而得到最优解，容易早熟收敛。而广义遗传算法摒弃了新达尔文主义学说对突变作用的看法，相信选择、定向交换和定向突变的协同作用是实现快速进化的合理方式。广义遗传算法首次将结果反馈引入操作程序，并通过它对选择、交换和突变的工作方式进行自适应调节［3］。因此文中采用了广义遗传算法［4］。

在进化程序上，广义遗传算法和经典遗传算法有所不同。经典遗传算法的进化程序为:双亲选择→基因交换→基因突变→生存选择→下一代种群;广义遗传算法的进化程序为:双亲选择→基因交换→一家4口→2/4生存选择→基因突变→一家4口→2/4生存选择→下一代种群。也就是说，广义遗传算法将选择原则贯彻于整个生命周期［3］。具体算法程序流程［5］如图1所示。

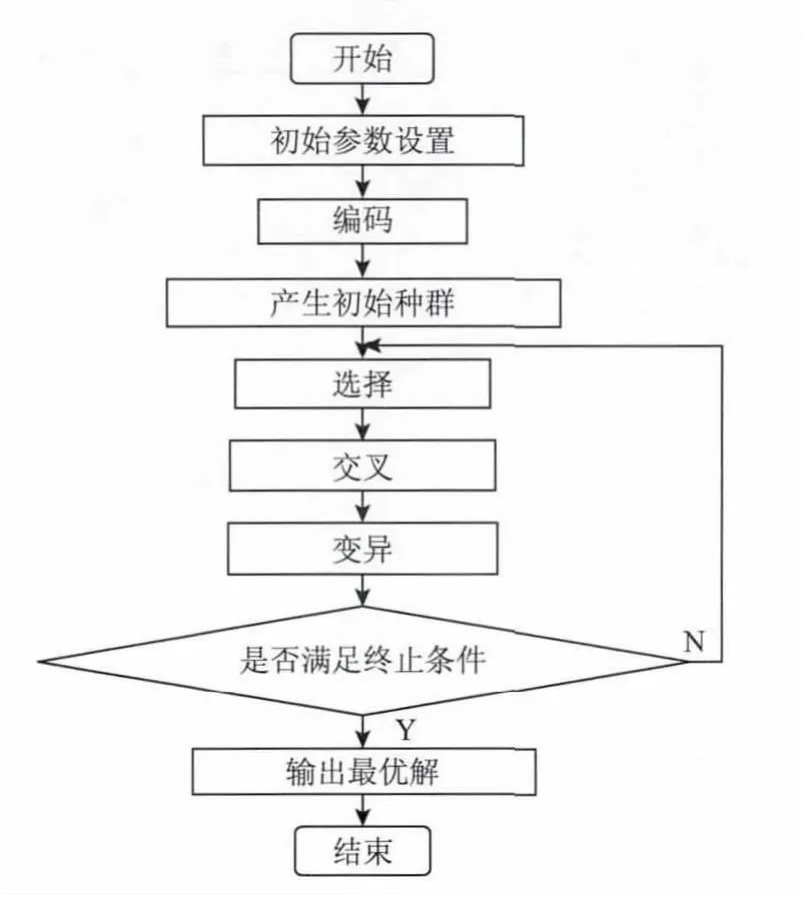
图1 遗传算法基本操作流程Fig．1 Flowchart of the genetic algorithm

与经典遗传算法相比，广义遗传算法采用了2/4择优的方式。2/4的选择是指每经过一次选择都允许父辈中的优良者和子代的优良者一同进入下一轮的竞争。意即两个父辈经过交叉和变异产生了两个新的子代，组成一家4口，然后按照适应度一家4口进行选择和淘汰后产生两个新的子代进入下一代。

考虑一般非线性模型的优化问题［6］:

其中:{cj}为模型 p个待优化参数，cj∈［aj，bj］，j=1，2，…，p;X为模型N维输入向量;Y为模型M维输出向量;f为一般非线性模型，即f:RN→RM{(Xi，Yi)|i=1～m}为模型m对输入、输出观测数据;‖·‖为取范数;q为实常数，视实际优化准则要求而定;Q为优化准则函数。

1．2 算法步骤

1．2．1 编码 若采用二进制编码，则码串会很长，编码和解码操作将占用较多时间，而且码串过长会使算法的搜索效率降低。对于连续变量的优化问题，实数编码有高精度、便于大空间搜索、表示更加自然的优点，并且计算精度不会受到编码方式的影响。因此，文中采用实数编码。

1．2．2 初始群体设定 给定优化参数的搜索范围，在此范围之内随机、均匀地选择n对参数作为初始父代。其中cj为第j条染色体对应的基因。

1．2．3 评价 通常的评价标准是指优化准则函数与传统寻优方法的“适应度”，因群体中每个个体代表一种决策，所以将第i个个体代入式(1)得到相应的优化准则函数Pi。Pi值越小，说明该个体的适应性能越强。

1．2．4 选种 按优化准则函数值进行从小到大的排序，将排在最前面的几个个体称为优秀个体。构造函数Qi使其与优化准则函数Pi成反比且满足Qi＞0和Q1+Q2+…+Qn=1。从这些父代个体中以概率Qi选择第i个个体，共选择两组各n个个体。

1．2．5 交叉 将随机选中的双亲进行杂交，最简单的杂交方法是随机地选取一个截断点，将双亲的基因码链在截断点切开，然后交换其尾部，由杂交产生的新染色体数仍为n。

1．2．6 选择 采用2/4择优方式选择。即允许父辈中的优良者和子代的优良者一同竞争，将优化准则函数值中n个P值较大的淘汰掉。

1．2．7 变异、选择 从n条经选择后的染色体中随机选取若干个体，对选中的个体，随机选择某一位进行取反运算产生新的个体，这样便完成了变异操作。之后对2n个个体又进行2/4择优方式选择。

1．2．8 迭代 由上步得到的n个子代个体作为新的父代，重复第(1．2．3)～ 第(1．2．7)步骤，生成下一代→重新评价→选种→交叉→选择→变异→选择，直到准则函数P不再变化或新一代中的最小P值与上一代中的最小P值满足一定精度要求，迭代过程终止，计算结束。最后一代中函数对应的个体为最优秀的个体。

2 工程实例应用

某高速公路是国家重点工程项目，公路沿线多为山丘区，地形起伏大，高填方路段较多，有些路段经过稻田、水塘、老河道，下有比较厚的淤泥层，在路基填筑后，这些路段固结沉降持续时间较长，且容易产生不均匀沉降。为此，沿线共布设了208个沉降观测点，对路段的沉降进行监测，以便掌握路基的沉降规律和趋势、控制和安排施工进度。文中以路基沉降观测中的H026号测点(具体位置为K48+260右侧路肩)为例进行路基沉降预测。该观测点于2010年7月2日布设，第一次观测时间是2010年7月12日，第12次观测时间是2011年7月3日，每次间隔1个月。文中用以下的指数模型［7］来表示沉降规律:

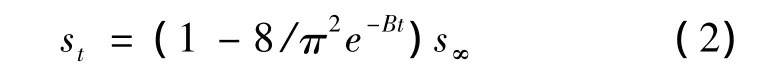
其中，t为沉降时间，d;st为时间t的沉降量，mm;s∞为软土地基最终沉降量，mm;B，s∞为模型参数。根据观测数据{(t，st)}来解式(2)的B和s∞，可以构造优化准则函数:

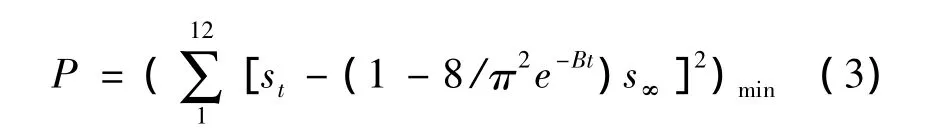
根据上述原理和步骤进行迭代［8-9］，在计算过程中，选取父代个体数目为200、优秀个体数目为10和变异概率为0．2，给定 B和s∞的变化区间，通过广义遗传算法，最后得到H026号的最优化估计结果如表1所示。

表1 广义遗传算法的计算结果Tab．1 Results of the generalized genetic algorithm

在得到观测点的沉降计算模型优化参数后，即首先确定了最终沉降量(s∞)。对于本例，最终沉降量是394 mm，同时可求得任一时刻t的沉降量。通过表2可知，上述方法的拟合度是很高的。为了比较遗传算法在模型参数优化方面的精度，分别用线性回归、灰色预测［10］估计式(3)的B和s∞，最后得到的拟合情况如图2所示。

表2 H026号点观测值与广义遗传算法的拟合值Tab．2 Observed values and the fitted values of the generalized genetic algorithm for No．H026

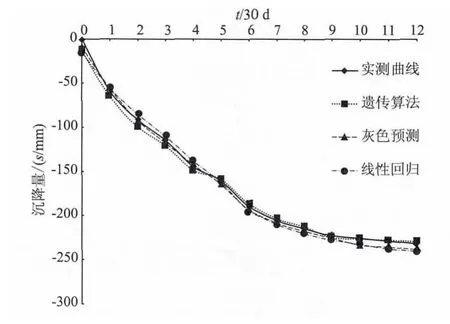
图2 不同方法估计参数拟合沉降曲线Fig．2 Settlement curves for different methods

3 结语

1)算例表明，广义遗传算法作为软土地基沉降计算的全新算法，只要给出一个合理的最终沉降量的合理范围，就能较好地得到全局最优解。它的编码操作保证在每一步迭代时能充分利用每群解中的信息，且具高效并行性。另外，引入实数编码又使问题表述更加自然。

2)广义遗传算法能搜索成群的解，并且在搜索过程中不断向可能包含最优解的方向调整搜索空间，使之有条件求得全局意义上的最优解，有效避免了常规方法易陷入局部极值的缺陷，提高了收敛效率。但是其收敛速度和解的精度受控于某些参数的选取。

3)从拟合曲线可以看出，广义遗传算法在预测长期沉降时较其它方法精度高，预测结果更具可靠性。

4)遗传算法在求解多参数非线性优化问题时对目标函数没有苛刻要求，故其适用范围比较广。但作为一种新工具应用于路基沉降分析中，有关问题还需进一步研究和完善。

［1］John H Holland．Adaptation in Natural and Artificial Systems［M］．Cambridge，Massachusetts:MIT Press，1992．

［2］高玮，郑颖人．采用快速遗传算法进行岩土工程反分析［J］．岩土工程学报，2001，23(1):120-122．GAO Wei，ZHENG Yinren．Back analysis in geotechnical engineering based on fast convergent genetic algorithm［J］．Chinese Journal of Geotechnical Engineering，2001，23(1):120-122．(in Chinese)

［3］董聪，郭晓华．广义遗传算法的逻辑结构及全局收敛性的证明［J］．计算机科学，1998，25(5):38-42．DONG Cong，GUO Xiaohua．Logic structure of generalized genetic algorithm and a proof of its global convergence［J］．Computer Science，1998，25(5):38-42．(in Chinese)

［4］李鹏，董聪．基于实数编码的广义遗传算法及其在优化问题中的应用［J］．控制与决策，2002，17(4):487-490．LI Peng，DONG Cong．Real coding based generalized genetic algorithm and its application in optimization problems［J］．Control and Decision，2002，17(4):487-490．(in Chinese)

［5］赖道平，顾冲时，吴中如．基于偏最小二乘法的遗传模拟退火算法及其在大坝安全监控中的应用［J］．长江科学院院报，2003，20(3):47-49，58．LAI Daoping，GU Chongshi，WU Zhongru．Genetic simulated annealing algorithm based on partial least squares and its application in dam safe monitoring［J］．Journal of Yangtze River Scientific Research Institute，2003，20(3):47-49，58．(in Chinese)

［6］刘勇健．遗传算法在软土地基沉降计算中的应用［J］．工业建筑，2001，31(5):39-41．LIU Yongjian．Application of genetic algorithm to calculation of soft soil ground settlement［J］．Industrial Construction，2001，31(5):39-41．(in Chinese)

［7］高大钊．土力学可靠性理论［M］．北京:中国建筑工业出版社，1989．

［8］徐士良．FORTRAN常用算法程序集［M］．北京:清华大学出版社，1991．

［9］黄运飞，冯静．计算工程地质学［M］．北京:兵器工业出版社，1992．

［10］景宏君，苏如荣，苏霆．高路堤沉降变形预测模型研究［J］．岩土力学，2007，28(8):1762-1766．JING Hongjun，SU Rurong，SU Ting．Study of settlement deformation prediction model of high embankment［J］．Rock and Soil Mechanics，2007，28(8):1762-1766．(in Chinese)