永磁同步电机分数阶智能积分调速控制
薛薇, 李永丽, 路鸦立
(1.天津大学电气与自动化工程学院,天津 300072;2.天津科技大学自动化系,天津 300222)
永磁同步电机分数阶智能积分调速控制
薛薇1,2, 李永丽1, 路鸦立2
(1.天津大学电气与自动化工程学院,天津 300072;2.天津科技大学自动化系,天津 300222)
永磁同步电机是一个多变量、非线性、强耦合的系统,对外界扰动及内部参数变化非常敏感。为改善其调速系统的动、静态性能,提高系统鲁棒性,提出了一种新的调速控制方法—分数阶智能积分控制策略。该控制策略是将比例作用与分数阶智能积分作用相结合,构成了分数阶智能积分控制器(PⅡλ)。相对于PI控制器,分数阶智能积分控制器可以获得更好的控制效果。仿真试验结果表明,分数阶智能积分控制器不仅能够快速、精确地跟踪给定速度,而且对负载扰动及参数变化具有更好的抗扰性和鲁棒性。
分数阶微积分;智能积分;永磁同步电机;调速
0 引 言
永磁同步电机(permanent magnet synchronous motor,PMSM)具有体积小、结构简单、功率因数高以及运行可靠等优点,被广泛应用于工业过程中。但由于永磁同步电机属于多变量、强藕合、非线性系统,而常规PID控制器是基于线性理论设计的,只能在有限的范围内得到较好的控制效果,且易受电机参数变化和负载扰动等不确定因素的影响,因此,采用常规PID控制策略无法获得理想的控制效果。所以,永磁同步电机的先进控制策略一直是近年来的研究热点。文献[1]提出了一种基于小波神经网络的自适应Smith预估控制器,通过对模型误差的补偿,可以消除模型不确定性的影响。文献[2]使用积分滑模控制实现dq轴电流解藕,可以提高系统在运动过程中对参数摄动和外界扰动的鲁棒性。文献[3]将滑模变结构应用于永磁同步电机伺服系统的位置控制中,并结合一种新的滑模增益设计方法来改善滑模控制的鲁棒性。文献[4]在常规模糊控制器的基础上将智能积分引入到永磁同步电机矢量控制系统中,使系统在保留常规模糊控制良好的动态性能的同时改善了稳态精度。文献[5]利用输入输出解藕线性化技术将永磁同步电机模型转化为线性模型,然后基于线性模型设计了H∞鲁棒控制器,可以提高系统对内埋式永磁同步电机参数变化的鲁棒性。文献[6]提出了一种无需参数整定的自抗扰控制器(NMT-ADRC),将其应用到永磁同步电机调速控制系统中,能够有效地控制永磁同步电机的转速和转矩。
现实系统中许多被控对象具有非线性并存在具有记忆功能的元器件,对于这样的被控对象用分数阶微分方程能更准确地描述其动态特性,也就是说,这样的系统在严格意义上是分数阶的。理论上用分数阶控制器去控制分数阶被控对象,可以获得更好的控制效果。另外,由于分数阶控制器的控制自由度比传统整数阶控制器大,因此,分数阶控制器对整数阶被控对象同样可以获得更好的控制效果。随着分数阶微积分理论的不断发展,分数阶微积分的应用已渗透到许多工程领域。文献[7]针对输入输出受限和不确定性的非线性锅炉-汽轮机系统设计分数阶PIλDμ控制器,仿真结果表明采用粒子群优化算法进行参数整定的分数阶PIλDμ控制器在大范围负荷变化及存在参数、结构不确定性时,系统均能取得满意的控制效果。文献[8]采用遗传算法优化整定分数阶PIλ控制器,对风电场无功补偿的STATCOM进行电压控制,可以有效地抑制风电场电压波动,提高风电场的安全稳定运行能力。文献[9]和[10]分别采用参数图解法和H∞设计法对时滞系统的分数阶PIλ控制器和PDμ控制器进行参数整定与设计,并给出了理论分析与实例验证,为分数阶控制器的应用提供了理论基础。
本文用分数阶微积分代替智能积分中的整数阶积分,通过分数阶智能积分环节与传统比例环节并联的形式,构成了一种分数阶智能积分控制器(简记为PⅡλ)。该控制器在保证获得较好系统动、静态性能的同时,可提高系统的鲁棒性和抗扰性。
1 分数阶智能积分器
1.1 分数阶微积分
连续分数阶微积分算子如下:
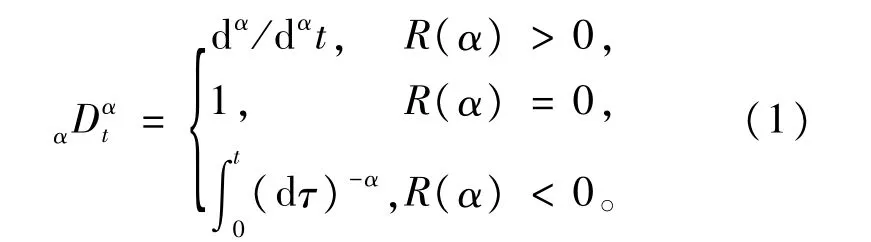
式中,α和t为分数阶微积分算子αDαt的上下限;α为任意数。
常用的分数阶微积分的定义有:
(1)Grunwald-Letnikov定义
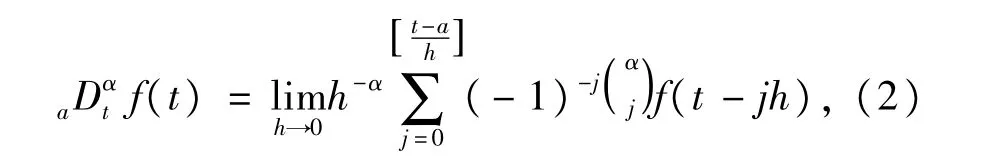
(2)Riemann-Liouville定义
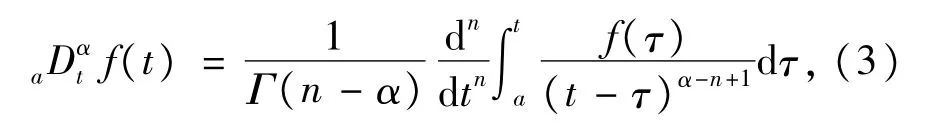
其中:n-1<α<n,Γ(.)为Gamma函数。
(3)Caputo定义

由定义可见,分数阶微积分理论和整数阶微积分理论存在很大的区别,分数阶微积分具有显著的记忆性,它不仅与当前时刻有关,还与以往时刻有关,而整数阶微积分只与当前时刻有关。
本文采用Riemann-Liouville分数阶微积分的定义,在零初始条件下进行拉普拉斯变换得到

由此得到分数阶积分环节的传递函数为:

式中,ki为积分系数,λ(0<λ<1)为分数阶控制器的阶次。
1.2 智能积分
在控制系统中,为了消除系统残差,往往加入积分环节。但由于控制系统的动态过程是不断变化的,固定的积分作用会使系统的稳定性和快速性变差。所以为了获得良好的控制性能,控制系统应该根据系统的状态,不断地调整控制策略[11]。
以二阶系统为例说明智能积分作用原理,图1所示为一个典型二阶系统的单位阶跃响应曲线,在AB段和CD段,系统有偏离稳态值的趋势,此时应该加入适当的积分控制,使系统向稳态值靠近;而在BC段和DE段,系统自身有减少误差向稳态值靠近的趋势,这时可以把积分作用去除掉。这样的积分作用的引入具有仿人智能的效果,称之为智能积分(Intelligent Integration,简称II)[12]。

图1 典型二阶系统单位阶跃响应曲线Fig.1 Typical second order system in unit step response curve
由于分数阶积分环节的传递函数中涉及时间步长的累加,所以分数阶智能积分控制器能对工业生产中的时变环节起到良好的控制作用。这些优势,对于传统PI控制器来说并不具备。
1.3 分数阶智能积分器
本文所采用分数阶智能积分控制器的原理结构图如图2所示。

图2 分数阶智能积分控制器原理结构图Fig.2 Structure diagram of PⅡλ
分数阶智能积分控制器的传递函数为:
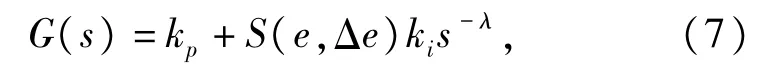
式中,kp为比例系数,ki为积分系数,λ(λ>0)为分数阶控制器的阶次,e为转速误差,Δe为转速误差变化率,S(e,Δe)是开关函数,其定义为
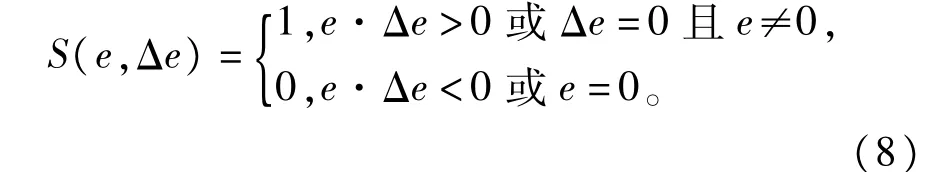
智能积分和分数阶微积分均具有“记忆性”,分数阶智能积分控制器可以记住有用的信息,略去无用的信息,具有更好的仿人智能控制作用。
2 永磁同步电机数学模型
永磁同步电机在两相旋转dq坐标系下的定子电压方程为:
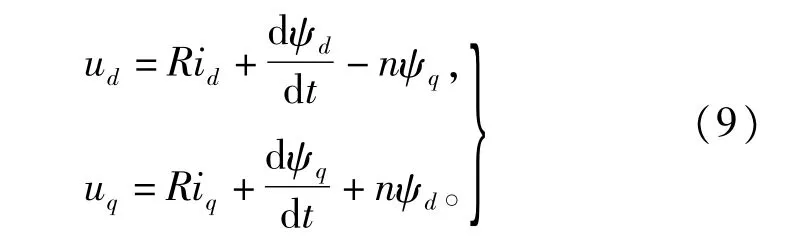
电磁转矩方程:
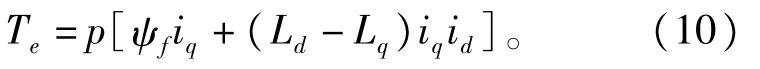
式中:ud,uq为定子电压在d、q轴上的分量;id,iq为定子电流在d、q轴上的分量;ψd,ψq为定子磁链在d、q轴上的分量;Ld,Lq为定子电感在d、q轴上的分量;R为定子电阻;ψf为转子磁链在d轴上的藕合磁链;p为磁极对数。
由式(10)可知,由于永磁同步电机转子磁链恒定不变,所以调节id或iq就可以有效地调节电机的转速。这里采用id=0的控制方式,把定子电流矢量始终控制在q轴上,根据式(10),电磁转矩只与定子电流的幅值成正比[13]。
当采用id=0的矢量控制时,转子定向在dq旋转坐标系的转速方程为:

仿真中电机参数为:极对数4;定子电阻0.9585Ω;直、交轴同步电感5.2mH;转动惯量0.000 63(kg.m2);转子磁场系数0.18Wb。
3 PMSM的分数阶智能积分调速控制
图3为永磁同步电机的矢量调速系统原理框图,系统采用转速与电流双闭环级联控制结构。电流环应用常规PI控制策略,对电流采用id=0的矢量控制方法,通过调节iq实现对电磁转矩的控制;转速环采用本文提出的分数阶智能积分控制策略,分数阶微积分和智能积分均具有记忆功能,通过它们可以减小电机参数变化及外部扰动等因素对控制系统的影响。

图3 控制系统原理框图Fig.3 Structure diagram of system
4 仿真试验
为了验证所设计控制器的性能,在Matlab/Simulink中建立PMSM空间矢量脉宽调制仿真模型,并对其进行仿真验证。永磁同步电机矢量控制系统的仿真结构图如图4所示。
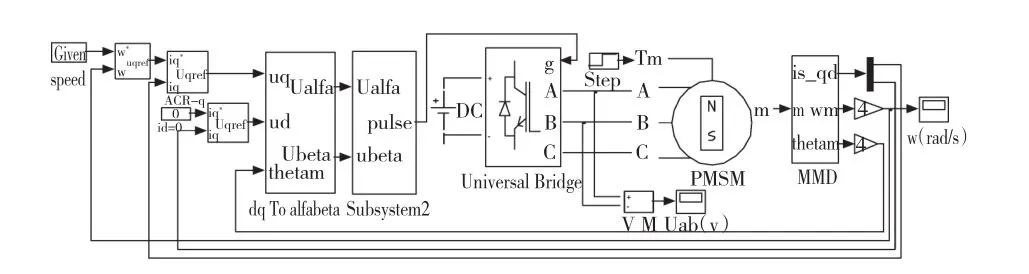
图4 永磁同步电机仿真结构图Fig.4 Simulation model of PMSM
仿真中对控制器阶次λ进行多次调整,λ在[0.8,1.1]的范围内变化,仿真结果证明λ=0.9时控制器的控制效果最好,控制器其它各参数取值如下:
电流环d轴PⅠ控制器:比例系数kp=10.3,积分系数ki=2.1;电流环q轴PⅡ控制器的参数:比例系数kp=11.2,积分系数ki=2.3;
速度环PⅡλ控制器的参数:比例系数kp= 0.006,积分系数ki=24.5,λ=0.9;
速度环PⅡ控制器参数:比例系数kp=0.006 4,积分系数ki=0.5;
速度环PⅠ控制器参数:比例系数kp=0.02,积分系数ki=0.003。
为了验证本文提出的PⅡλ控制策略的有效性,这里把PⅡλ控制策略与传统的PⅠ控制策略以及整数阶比例智能积分控制策略(简记为PⅡ)进行比较。
1)试验一
系统空载启动,给定转速n=800 r/min,进入稳态后,在t=0.3 s时突加负载TL=4 N.m,得到系统响应曲线如图5所示。
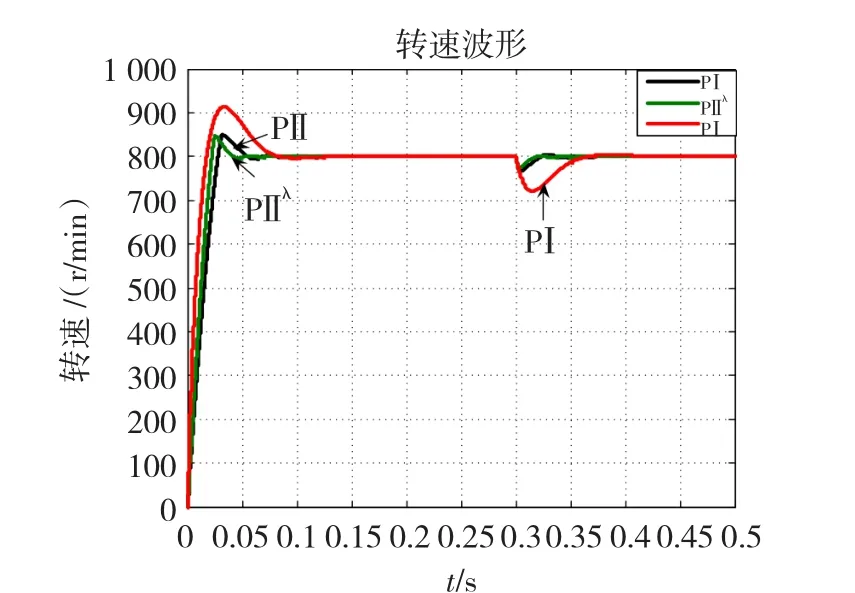
图5 负载突变时系统响应曲线Fig.5 Speed waveform w ith load changing
2)试验二
t=0时刻,给定转速n=600 r/min,电机空载启动,在t=0.15 s时,转速跳变到n=1 000 r/min,得到系统响应曲线如图6所示。

图6 转速突变时系统响应曲线Fig.6 Speed waveform w ith speed changing
3)试验三
系统空载启动,速度给定设置为矩形波,图7、图8给出了频率为5 Hz,转速为800 r/min时,得到的系统响应曲线和误差曲线。
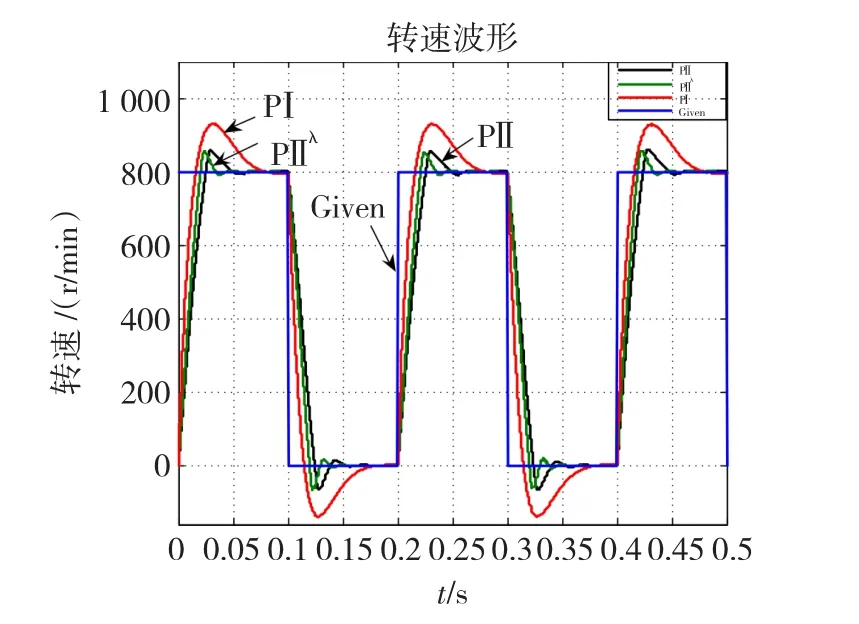
图7 跟踪矩形波时系统响应曲线Fig.7 Speed waveform w ith rectangular

图8 跟踪矩形波时系统误差曲线Fig.8 Speed error waveform w ith rectangular
4)试验四
系统空载启动,速度给定设置为矩形波,图9、图10给出了频率为5 Hz,转速为1 000 r/min时,得到的系统响应曲线和误差曲线。

图9 跟踪三角形波时系统响应曲线Fig.9 Speed waveform w ith triangle

图10 跟踪三角形波时系统误差曲线Fig.10 Speed error waveform w ith triangle
5)试验五
电机在运行过程中,因受到环境、温度等因素的影响,某些参数数值会发生变化,当电机的电阻由R=0.958 5Ω变为R=1.958 5Ω,系统跟踪给定阶跃信号时的动、静态特性及抗扰性如图11、图12所示,其中给定转速n=800 r/min,t=0.3 s时突加负载TL=2 N.m。
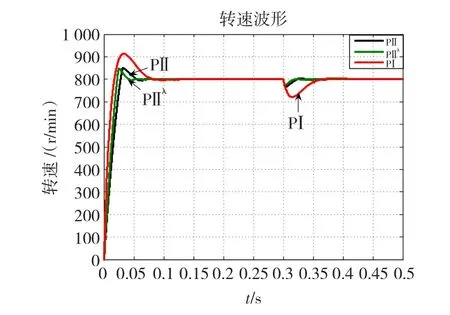
图11 电阻变化后系统响应曲线Fig.11 Speed waveform w ith R changing
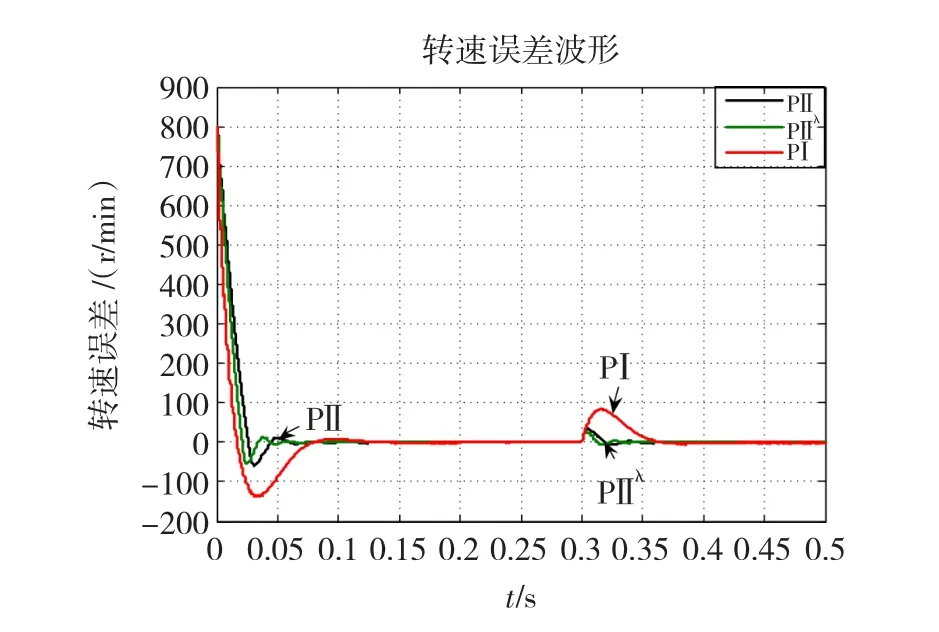
图12 电阻变化后系统误差曲线Fig.12 Speed error waveform w ith R changing
6)试验六
当电机的电感由L=5.2mH变为L=4.2mH,系统跟踪矩形波,转速为800 r/min,频率为5 Hz,得到的系统响应曲线和误差曲线如图13、图14。
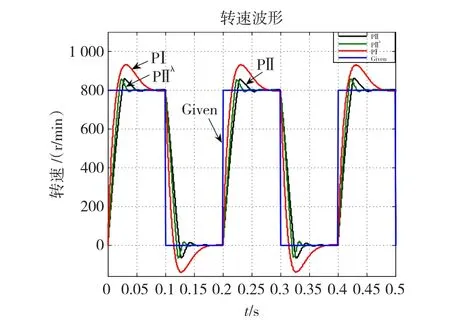
图13 电感变化后系统响应曲线Fig.13 Speed waveform w ith L changing

图14 电感变化后系统误差曲线Fig.14 Speed error waveform w ith L changing
7)试验七
当电机的磁链由ψf=0.18Wb变为ψf=0.14Wb,系统跟踪矩形波,转速为800 r/min,频率为5 Hz,得到的系统响应曲线和误差曲线图15、图16。

图15 磁链变化后系统响应曲线Fig.15 Speed waveform w ithψfchanging
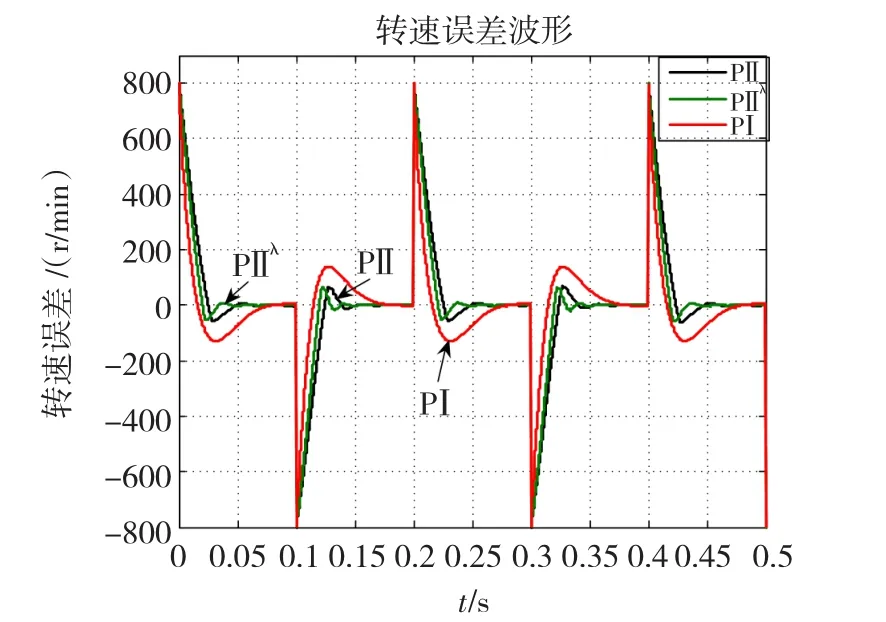
图16 磁链变化后系统误差曲线Fig.16 Speed error waveform w ithψfchanging
由图5~图16可知,PⅡλ控制器的控制效果要优于传统PⅠ控制器和智能积分PⅡ控制器。当负载发生变化时,PⅡλ控制器的转速降落较小,且其调整时间最短;当给定转速发生变化时,PⅡλ控制器的调整时间最短且超调量最小;对于特殊的给定转速,如矩形波和三角波,PⅡλ控制器的误差小于传统PⅠ控制器和PⅡ控制器,充分地显示了其高效的跟踪特性;当电机参数发生变化时,PⅡλ控制器仍能获得满意的控制效果。
总的来说,相比于PⅠ控制器,PⅡλ控制器和PⅡ控制器可以根据系统的动态特性,不断的调整控制策略,从而兼顾系统的动态品质和稳态精度;相比于PⅡ控制器,PⅡλ控制器多了一个可调参数λ,参数整定范围变大,控制器可以根据被控对象的数学模型选择合适的λ,获得更好的控制效果。
5 结 论
本文以永磁同步电机调速控制系统为研究对象,将分数阶微积分理论与智能积分思想相结合,并采用分数阶智能积分与比例环节并联形式构成分数阶智能积分控制器。通过仿真试验表明,与传统PⅠ转速控制器及整数阶比例智能积分PⅡ控制器相比,分数阶智能积分PⅡλ控制器具有更好的稳定性、快速性、抗扰性与鲁棒性,应该具有更广阔的发展前景。
[1] 刘达,李木国.带有扰动补偿的永磁同步电机自适应预测控制[J].电机与控制应用,2012,3(1):31-35. LIU Da,LI Muguo.Adaptive predictive control of permanent magnet synchronousmotorwith disturbance compensation[J].Motor and Control Application,2012,3(1):31-35.
[2] 周华伟,温旭辉,赵峰,等.基于内模的永磁同步电机滑模电流解藕控制[J].中国电机工程学报,2012,32(15):91-99. ZHOU Huawei,WEN Xuhui,ZHAO Feng,et al.Decoupled current control of permanentmagnet synchronousmotor driveswith slidingmode control strategy based on internal model[J].Proceedings of the CSEE,2012,32(15):91-99.
[3] 欧阳叙稳,尹华杰.基于变指数趋近律的永磁同步电机滑模控制研究[J].微电机,2011,44(9):31-34. OUYANG Xuwen,YIN Huajie.Slidingmode control research of pmsm based on variable exponential rate reaching law[J].Micromotors,2011,44(9):31-34.
[4] 王迪,王旭东.引入智能积分器的PMSM模糊控制系统[J].电机与控制学报,2010,14(10):100-106. WANG Di,WANG Xudong.Fuzzy logic control system with intelligent integrator for permanent magnet synchronous motor[J]. Electric Machines and Control,2010,14(10):100-106.
[5] 林立,黄苏融.永磁同步电机系统线性化H∞鲁棒控制[J].电机与控制学报,2009,13(4):541-547,552. LIN Li,HUANG Surong.Robust control with linearization technique for interior permanentmagnet synchronousmotor servo system[J].Electric Machines and Control,2009,13(4):541-547,552.
[6] 卢达,赵光宙,曲轶龙,等.永磁同步电机无参数整定自抗扰控制器[J].电工技术学报,2013,28(3):27-34. LU Da,ZHAO Guangzhou,QU Yilong,et al.Permanentmagnet synchronousmotor control system based on nomanual tuned active disturbance[J].Transactions of China Electrotechnical Society,2013,28(3):27-34.
[7] 王东风,王晓燕,韩璞.锅炉-汽轮机系统的分数阶控制器设计[J].中国电机工程学报,2010,30(5):113-119. WANG Dongfeng,WANG Xiaoyan,HAN Pu.Design of fractional order controllers for a boiler-turbine system[J].Proceedings of the CSEE,2010,30(5):113-119.
[8] 孙勇,范国英,孙其振,等.用于风电场无功功率补偿的STATCOM分数阶控制器设计[J].电力系统保护与控制,2012,40 (16):54-58,64. SUN Yong,FAN Guoying,SUN Qizhen,et al.Fractional order controller design of STATCOM for reactive power compensation of wind farm[J].Power System Protection and Control,2012,30(5):54-58,64.
[9] WANG Dejin,ZHANG Jinghui.A graphical tuning of PI controllers for fractional-delay systems[J].J Control Theory Appl,2011.9(4):599-603.
[10] WANG Dejin,GAOXueli.H∞design with fractional-order PDμcontrollers[J].Automatica,2012(48):974-977.
[11] 钟汉如,周其节,钟慕良.智能积分方法在精密注塑机控制中的应用[J].华南理工大学学报:自然科学版,1997,25(9):6 -9. ZHONG Hanru,ZHOU Qijie,ZHONG Muliang.Application of intellectual integrtion in injectionmachine control[J].Journal of South China University of Technology:Natural Science,1997,25(9):6-9.
[12] ZHANG Juping,LU Yali,XUE Wei,et al.Fuzzy neural network control of cold tandem rolling thickness based on the intelligent integration[J].Applied Mechsnics and Materials,2013,278-280:1585-1592.
[13] 陈振,耿洁,刘向东.基于积分时变滑模控制的永磁同步电机调速系统[J].电工技术学报,2011,26(6):56-61. CHEN Zhen,GENG Jie,LIU Xiangdong.An Integral and exponential time-varying sliding mode control of permanentmagnet synchronousmotor[J].Transactions of China Electrotechnical Society,2011,26(6):56-61.
(编辑:张诗阁)
Application of fractional intelligent integral controller for PMSM
XUEWei1,2, LIYong-li1, LU Ya-li2
(1.School of Electrical Engineering and Automation,Tianjin University,Tianjin 300072,China) 2.Department of Automation,Tianjin University of Science and Technology,Tianjin 300222,China)
The permanentmagnet synchronousmotor(PMSM)is amultivariable and nonlinear system with strong coupling.It’s sensitive to interference and parameters variation.To improve the system static,dynamic performance and robustness,a new speed control strategy-fractional intelligent integral strategy was proposed,which couples the proportion with fractional intelligent integration to constitute the fractional intelligent integral controller(PⅡλ).Compared with PI controller,the fractional intelligent integral controller achieves better control performance.The simulation results verify the fractional intelligent integral controller not only can track the given speed quickly and accurately,but also has better anti-interference and robustnesswith load and parameters variations.
fractional calculus;intelligent integration;PMSM;speed regulation
10.15938/j.emc.2015.05.010
TM 341
A
1007-449X(2015)05-0067-07
2013-10-09
国家自然科学基金项目(51177108,60874028);教育部博士点基金项目(20110032110066)
薛 薇(1963—),女,博士研究生,教授,研究方向为先进控制理论及其应用;自适应控制与智能控制;非线性系统分析与控制;
李永丽(1963—),女,博士,教授,博士生导师,研究方向为电力系统故障分析及电气设备故障诊断;电力系统微机保护;分布式发电系统并网、控制与保护技术;
路鸦立(1987—),女,硕士研究生,研究方向为先进控制理论及其应用。
薛 薇

