绕线转子无刷双馈电机的d-q轴数学模型
熊飞, 王雪帆, 华斌, 尹传涛
(1.华中科技大学强电磁工程与新技术国家重点实验室,湖北 武汉 430074; 2.中国船舶重工集团第七一二研究所,湖北 武汉 430064)
绕线转子无刷双馈电机的d-q轴数学模型
熊飞1, 王雪帆1, 华斌2, 尹传涛2
(1.华中科技大学强电磁工程与新技术国家重点实验室,湖北 武汉 430074; 2.中国船舶重工集团第七一二研究所,湖北 武汉 430064)
在阐述绕线转子无刷双馈电机的定子绕组、转子绕组结构和静止a-b-c轴数学模型的基础上,推导出电机的d-q轴数学模型。这种电机模型建立在一个任意d-q轴坐标系下,使用起来方便,消除定子绕组和转子绕组之间互感矩阵的时变系数,缩短计算时间,有利于控制方法的实现,适用于绕线转子无刷双馈电机动态和稳态性能的分析研究。d-q轴数学模型的参数能根据电机的设计几何尺寸和经验公式得到。通过仿真分析结果和实验数据的对比,验证了任意d-q轴数学模型的正确性。绕线转子无刷双馈电机任意d-q轴数学模型的建立为电机性能分析和控制策略的研究奠定基础。
无刷双馈电机;数学模型;绕线转子;d-q轴坐标系;仿真分析
0 引 言
无刷双馈电机是一种由两套不同极对数的定子绕组和一套转子绕组构成的新型交流感应电机。两套定子绕组分别称为功率绕组和控制绕组,转子可采用特殊笼型、磁阻转子或者绕线转子结构[1-3]。电机既能作为电动机运行,也能作为发电机运行,兼有异步电机和同步电机的特点。由于这种电机具有结构简单、坚固耐用、功率因数可调和变频器容量等级小等优点,它在交流变频调速以及船用轴带发电、水力发电和风力发电等领域有着广泛的应用前景[4]。
国内外学者对无刷双馈电机的数学模型进行了广泛的研究。文献[5]建立了6/2极特殊笼型转子无刷双馈电机在转子坐标系下的d-q轴模型,并对电机的起动和运行性能进行仿真研究。文献[6]将上述的转子坐标系下d-q轴模型推广至任意极对数的通用形式。文献[7]建立适用于双馈运行稳态计算的无刷双馈电机谐波分析模型来评估样机的性能,并建立有限元分析模型用于研究铁心的损耗和饱和问题[8]。文献[9]推导笼型转子和磁阻转子无刷双馈电机的统一等效电路与电磁转矩表达式,并对等效电路中的电感参数进行了实验验证。文献[10]从电机的基本定子线圈及笼型转子的基本回路出发,建立无刷双馈电机静止a-b-c轴数学模型,并给出相应的参数计算公式。文献[11]提出无刷双馈电机混合坐标系数学模型,为变频器-无刷双馈电机调速系统仿真计算提供了有力的理论工具。近年来,文献[12]提出用电动势来等效机械负载的新频率折算方法,建立通用的等效电路模型,并对电机的特性进行分析和仿真。文献[13]提出一种场路藕合运动问题的二维时步有限元方法,建立无刷双馈电机有限元分析模型。
根据绕线转子无刷双馈电机的特点,给出了电机的定子绕组、转子绕组结构和静止a-b-c轴数学模型。在此基础上,通过坐标变换,推导出任意d -q轴数学模型和d-q轴数学模型参数的计算方法。最后,通过仿真结果和实验数据来验证建立的任意d-q轴数学模型的正确性。
1 绕线转子无刷双馈电机的结构
1.1 定子绕组结构
无刷双馈电机的定子绕组结构有单绕组和双绕组两种结构。单绕组结构从一套定子绕组中引出两个三相的出线端口供电,从不同端口看进来,同一套绕组等效为不同极对数的绕组,较理想的连接方式为3Y/3Y和4Y/3Y两种连接方式,但这种结构在两种不同极对数下由于各并联支路感应电势不容易控制平衡会导致内部产生环流,因此现有的无刷双馈电机基本采用双绕组结构。双绕组结构是在定子槽中放有两套相互独立不同极对数的三相对称绕组,两套绕组能分别采用单层或者双层绕组、不同的并联支路和不同的节距进行灵活设计。图1给出一台定子72槽,功率绕组极对数为7和控制绕组极对数为5试验样机的定子绕组接线图。

图1 定子绕组接线图Fig.1 Stator w inding connection
1.2 转子绕组结构
转子结构是影响无刷双馈电机性能的一个重要因素。目前国内外无刷双馈电机的转子主要采用特殊笼型和磁阻转子两种结构,其中特殊笼型转子结构简单,加工制造容易,成本低廉,适用于制造大容量电机[14];磁阻转子结构坚固,转子由铁心冲片和永磁体构成,转子上没有导体和绕组,建模和控制简单;但这两种转子由于结构受到一定的限制,使得转子谐波含量难以控制,电机性能难以满足实用要求。当无刷双馈电机的转子采用绕线转子这种结构时,其能对电机中存在的两种不同极对数基波磁势相对大小、绕组系数和谐波含量等进行方便地设计、调整和控制,可以做到绕组导体利用率高,谐波含量低的优点。图2给出一台转子12槽,功率绕组极对数为7和控制绕组极对数为5试验样机的转子绕组接线图。
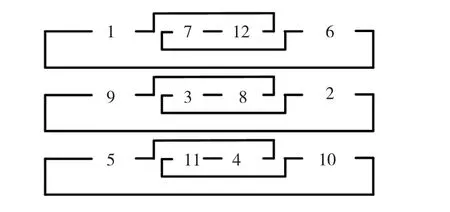
图2 转子绕组接线图Fig.2 Rotor w inding connection
2 d-q轴数学模型
2.1 静止a-b-c轴数学模型
为了得到绕线转子无刷双馈电机静止a-b-c轴数学模型的磁链方程和电压方程,作如下假定:
1)不计定子和转子齿槽影响,定子内表面和转子外表面圆滑,气隙均匀;
2)不计铁磁材料饱和、磁滞、涡流的影响,参数线性化;
3)定子绕组和转子绕组产生的磁动势为正弦波,忽略它们的谐波影响。
在上述假定的基础上,为简化分析,再假设转子绕组由三相对称绕组构成。根据基尔霍夫定律,按照电动机惯例定义参考方向,建立其磁链矩阵方程和电压矩阵方程为

式(1)和式(2)中,ψ表示磁链矩阵,U表示电压矩阵,I表示电流矩阵,Z表示阻抗矩阵,R表示电阻矩阵,L表示电感矩阵;下标abc表示abc三相有关的变量参数;下标p和c分别表示与功率绕组和控制绕组有关的变量参数,下标r表示与转子绕组有关的变量参数;下标pr表示功率绕组与转子绕组之间的互感参数,下标cr代表控制绕组与转子绕组之间的互感参数;上标T表示转置矩阵;d()/d t表示微分算子。
根据这种电机的原理和结构可知,电机可由功率绕组和控制绕组两个子系统构成。选取功率绕组和控制绕组子系统参考坐标系如图3所示,其中Ap、Bp、Cp和ap、bp、cp为功率绕组子系统中定子绕组和转子绕组三相轴线,Ac、Bc、Cc和ac、bc、cc为控制绕组子系统中定子绕组和转子绕组三相轴线,以功率绕组子系统中Ap轴线为参考轴,pp和pc分别为功率绕组和控制绕组的极对数,θr为转子旋转的机械角度,θspc+180°为功率绕组和控制绕组A相轴线之间的夹角。
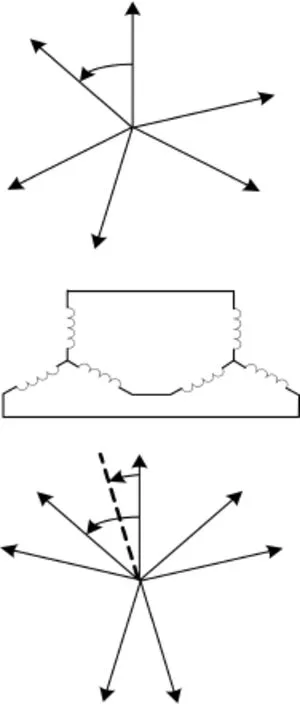
图3 功率绕组和控制绕组子系统的参考坐标系Fig.3 Three-phase stationary reference frames of the power w inding subsystem and the control w inding subsystem
根据文献[15]中的参数计算方法,推导出功率绕组、控制绕组和转子绕组的电阻矩阵为

功率绕组的互感矩阵Lp为

控制绕组的互感矩阵Lc为
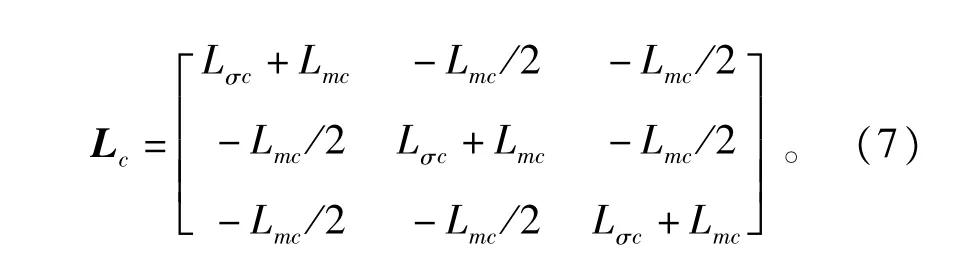
转子绕组的互感矩阵Lr为

功率绕组和转子绕组之间的互感矩阵Mpr为

控制绕组和转子绕组之间的互感矩阵Mcr为

式(3)~式(10)中,rp、rc和rr分别表示功率绕组、控制绕组和转子绕组一相的电阻值,Lσp、Lσc和Lσr分别表示功率绕组、控制绕组和转子绕组一相的漏电感;Lmp、Lmc和Lmr分别表示功率绕组、控制绕组和转子绕组一相的激磁电感;Lpr表示功率绕组和转子绕组相与相之间的互感;Lcr表示控制绕组和转子绕组相与相之间的互感。
电阻参数rp、rc和rr能根据电机的几何尺寸来计算,漏感参数Lσp,Lσcand Lσr与绕组端部漏磁、槽漏磁和谐波漏磁等漏磁通有关,可由经验公式估算或者试验方法测定,这里不作讨论。通过推导,功率绕组一相的激磁电感Lmp为
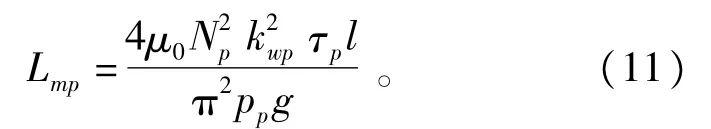
控制绕组一相的激磁电感Lmc为

转子绕组一相的激磁电感Lmr为
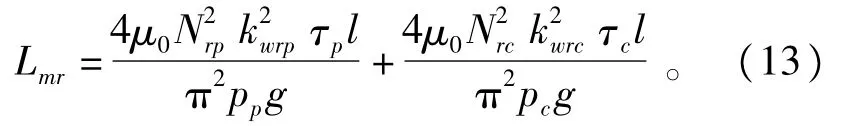
功率绕组和转子绕组相与相之间的互感Lpr为

控制绕组和转子绕组相与相之间的互感Lcr为

式(11)~式(15)中,g是气隙有效长度;l是铁心有效长度;τp和τc分别是定子功率绕组和控制绕组的极距;Np和Nrp分别是定子功率绕组和对应于功率绕组的转子绕组的每相串联匝数;Nc和Nrc分别是定子控制绕组和对应于控制绕组的转子绕组的每相串联匝数;Kwp和Kwrp分别是定子控制绕组和对应于控制绕组的转子绕组的绕组系数;Kwc和Kwrc分别是定子控制绕组和对应于控制绕组的转子绕组的绕组系数;μ0=0.4π×10-6H/m。
电机的电磁转矩方程为

电机的转子运动方程为

式(16)和式(17)中,Te表示负载转矩,ωr为转子的机械角速度,J表示电机的转动惯量,KD表示转子的机械阻尼系数,TL表示负载转矩。
2.2 任意d-q轴数学模型的推导
在上一节中,已经得到电机的静止a-b-c轴数学模型。由于功率绕组和转子绕组之间的互感矩阵、控制绕组和转子绕组之间的互感矩阵是转子位置角的函数,静止a-b-c轴数学模型是含有时变系数的微分方程组。为了使上述含有时变系数的微分方程组变换为易于求解的常系数微分方程组,常采用坐标变换。图4给出静止a-b-c轴坐标系与任意d-q轴坐标系的关系,其中ω为任意d-q轴坐标系轴线旋转的角速度,ωp为功率绕组电流的电角速度,ωc为控制绕组电流的电角速度。

图4 静止a-b-c轴坐标系与任意d-q轴坐标系的关系Fig.4 Relation between the arbitrary d-q axis reference frame and the stationary a-b-c axis reference frame
根据图3和图4可知,轴线Ap与d轴的夹角θ1为

轴线Ac与d轴的夹角θ2为

轴线ap与d轴的夹角θ3为
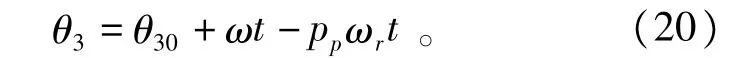
式(18)~式(20)中,θ10、θ20和θ30分别表示轴线Ap、轴线Ac、轴线ap与d轴的初始夹角。前面推导出的功率绕组和转子绕组之间的互感矩阵,控制绕组和转子绕组之间的互感矩阵已不考虑初始夹角的影响,这里令θ10=θ20=θ30=0。
根据上面的分析,变换分块矩阵为
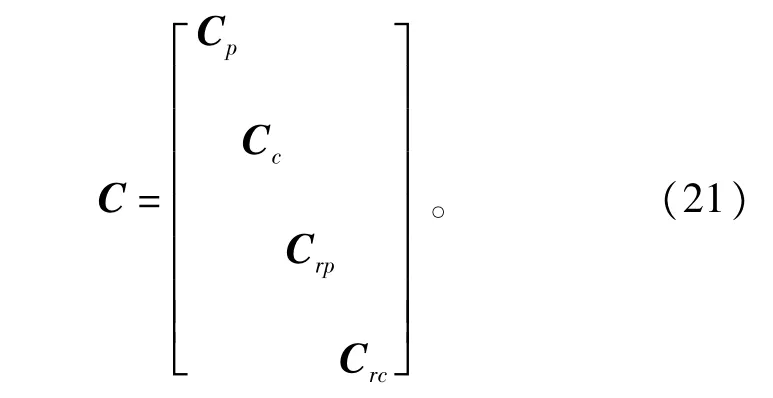
式(21)中,功率绕组变换矩阵Cp为

控制绕组变换矩阵Cc为
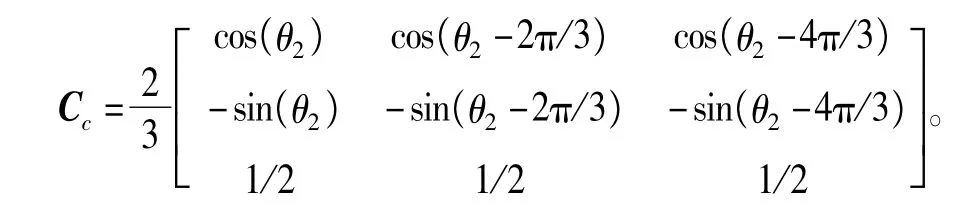
转子绕组变换矩阵Crp和Crc为

将转子绕组分成对应于功率绕组和控制绕组子系统的转子绕组,令

并定义

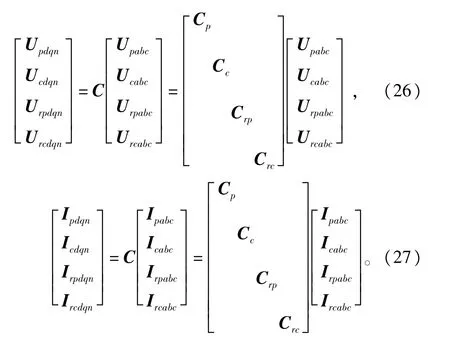
对式(1)和式(2)进行坐标变换,得到

式(28)和式(29)中,上标-1表示逆矩阵。
由于转子绕组自闭合形成回路,根据式(22)~式(24),对式(28)和式(29)中转子绕组进行合并,因此转子绕组磁链、电压和电流满足以下关系式

简化式(28)和式(29),根据以下关系式进行绕组折算,
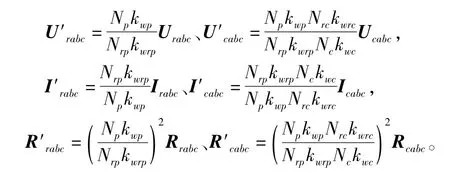
并令Mmp=3Lmp/2、Mmc=3L′mc/2、Lsp=Lσp+3Lmp/2、L′sc=L′σc+3L′mc/2和L′sr=L′σr+3L′mr/2,其中上标′表示折算到功率绕组的控制绕组或者转子绕组变量;假定系统三相对称,通过推导,得到转子绕组合并后的绕线转子无刷双馈电机在任意d-q轴坐标系下的磁链矩阵和电压矩阵方程为
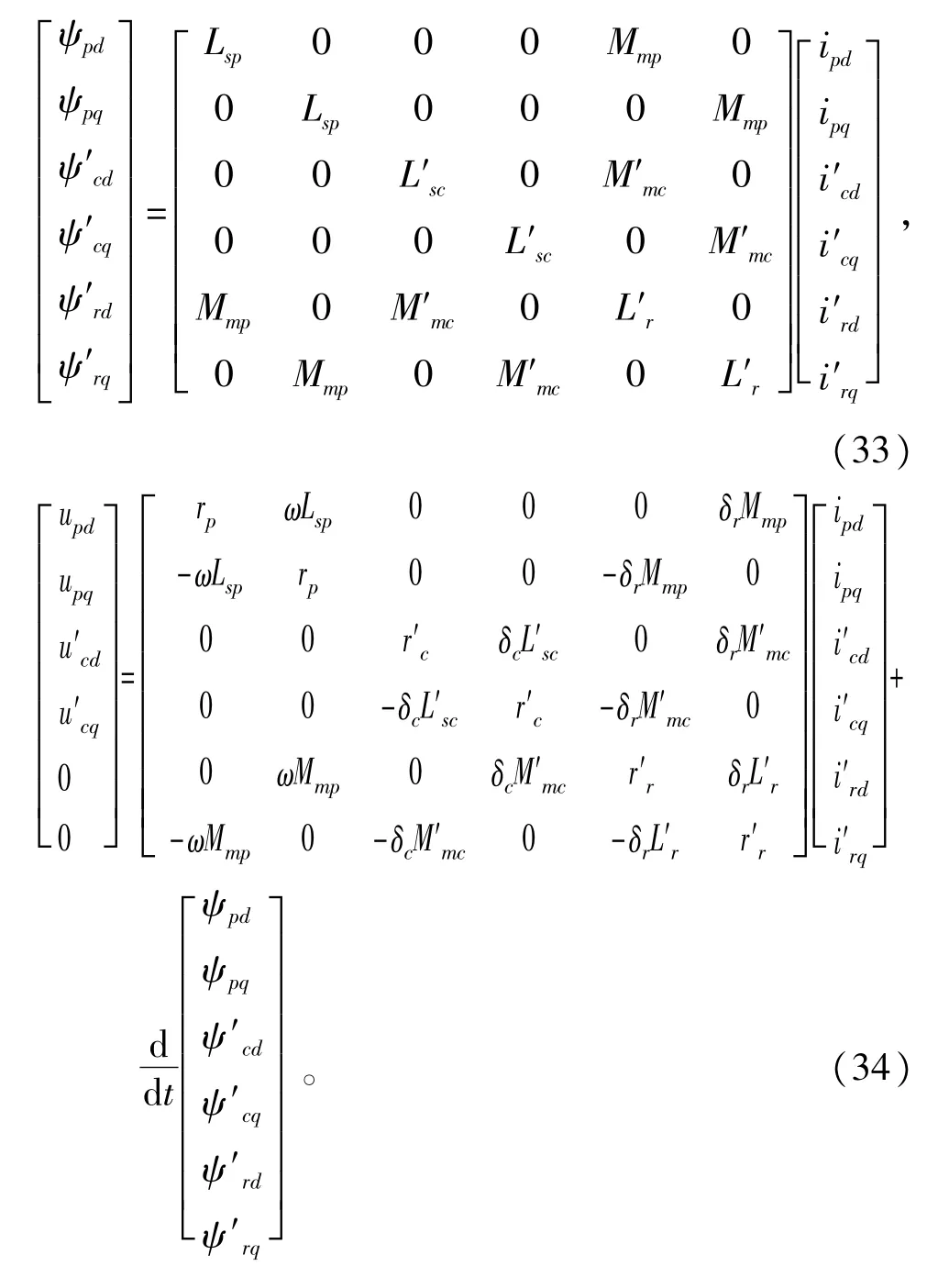
其中δc=ω-(pp+pc)ωr,δr=ω-ppωr。
对式(16)进行坐标变换,得到的电磁转矩方程为
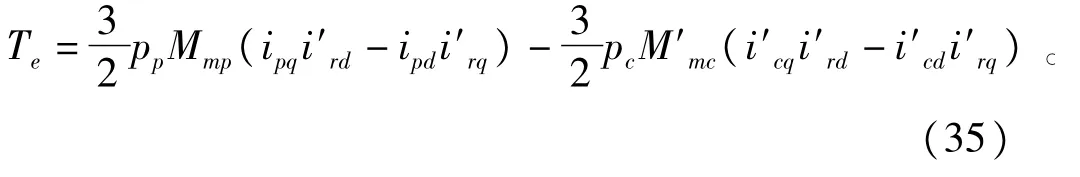
根据式(11)~式(15),通过绕组折算,d-q轴数学模型的参数计算公式为

当电机双馈同步稳定运行时,转子的机械角速度ωr与功率绕组电流的电角速度ωp和控制绕组电流的电角速度ωc满足以下关系式

电机的转子运动方程仍为式(17),不因坐标变换而变化。式(33)、式(34)、式(35)和式(17)构成绕线转子无刷双馈电机的任意d-q轴数学模型,选取不同的坐标轴能得到不同的坐标系。当参考坐标轴旋转的角速度为零,即ω=0,能构成静止α-β轴坐标系统;当坐标轴放在转子绕组轴线上,即ω= ppωr,能构成转子速d-q轴坐标系;当坐标轴放在以同步转速旋转的功率绕组轴线上,即ω=ωp=ωc+(pp+pc)ωr,能构成dc-qc轴同步速坐标系。任意d-q轴数学模型的建立消除定子绕组和转子绕组之间互感矩阵的时变系数,使用起来方便,缩短计算时间,有利于控制方法的实现,使得无刷双馈电机的分析变得和异步电机、同步电机一样简捷实用,能根据具体条件及问题性质采用不同的坐标变换方法加以应用。
3 样机仿真和试验研究
为验证上述d-q轴数学模型的正确性,设计了一台极对数为7/5的实验样机,定转子铁心冲片采用YZR200L的内外径尺寸,定子采用72槽,转子采用12槽。功率绕组、控制绕组和转子绕组的接线图如前图1和图2所示。电机d-q轴数学模型参数如表1所示。

表1 d-q轴数学模型参数Table 1 Param eters of them athem aticalmodel under the d-q axis reference frame
建立电机在dc-qc轴同步速坐标系下的动态仿真模型。采用转动惯量J=1.1 kg.m2,机械阻尼系数KD=0kg.m2/s。图5给出样机级联异步运行时,从理想空载起动到带负载转矩50 N.m的动态仿真工作特性曲线。

图5 样机异步运行时的仿真结果Fig.5 Sim ulation resultswhen the p rototypemachine is operating in the asynchronousmode
由图5可知,样机异步运行时,转速在250.7 r/min处稳定,当突加负载后,转速下降,并在238.2 r/min处稳定。当功率绕组、控制绕组和转子绕组相电流转换到dc-qc轴同步速坐标系下,稳定时dc-qc轴电流值均为恒定直流量。
图6给出样机双馈超同步速运行时,从异步空载起动、牵入到空载,控制绕组输出电压幅值为40 V、反相序、频率为2 Hz双馈运行,再到带负载转矩50 N.m的动态仿真工作特性曲线。由图6可知,样机双馈超同步速运行时,转速在260 r/min处稳定,这与式(37)是相吻合的。此时,功率绕组、控制绕组和转子绕组的dc-qc轴电流值稳定时也均为恒定直流量。

图6 样机双馈运行时的仿真结果Fig.6 Sim ulation resultswhen the p rototypemachine is operating in the doubly-fed mode
表2给出了不同运行方式下的仿真值与实测值对比结果。表2(b)中,样机双馈运行时,控制绕组输出电压幅值分别为20 V和40 V、反相序、频率为2 Hz。
从表2可以看出,仿真值与实测值比较吻合,说明了这一模型的正确性。当然,仿真结果与实测结果存在一定误差,这可能主要有以下几个方面的原因:1)这一模型是基于一定的理想假设条件,忽略功率绕组、控制绕组和转子绕组电机产生的谐波的作用;2)由于电机的电磁藕合模型复杂,实际电机的d-q轴数学模型参数难以准确给定;3)没有考虑磁场饱和温升等造成参数非线性化的影响。

表2 仿真值与实测值的对比Table 2 Com parison of simu lation and experimental data (a)样机异步运行时
4 结 论
基于以上对绕线转子无刷双馈电机的任意dq轴数学模型的研究,可以得出如下结论:
1)绕线转子无刷双馈电机的任意d-q轴数学模型具有良好的通用性与准确性,适用于绕线转子无刷双馈电机动态和稳态性能的仿真分析研究,对电机性能分析和控制策略的研究具有一定的指导意义;
2)样机的建模仿真和实验测试结果对比验证了这一建模方法的正确性,但由于这一模型是基于一定的理想假设条件,并且计算出的电机d-q轴数学模型参数有一定的偏差,因此导致仿真结果与实测数据存在一定误差。
[1] 徐芝纶.弹性力学[M].北京:高等教育出版社,1987.
[1] 韩力,高强,罗辞勇,等.不同转子结构无刷双馈电机的运行特性对比[J].电机与控制学报,2010,14(3):6-17. HAN Li,GAO Qiang,LUO Ciyong,et al.Comparasion on the performance of brushless doubly-fed machine with different rotor structures[J].Electric Machines and Control,2010,14(3):6 -17.
[2] 韩力,罗杰,李景灿,等.无刷双馈电机稳定性分析及其影响因素探讨[J].电机与控制学报,2012,16(3):22-29. HAN Li,LUO Jie,LIJingcan,etal.Stability analysis and its influence factors study of brushless doubly-fed machine[J].Electric Machines and Control,2012,16(3):22-29.
[3] 王雪帆.一种转子绕组采用变极法设计的新型无刷双馈电机[J].中国电机工程学报,2003,23(6):108-127. WANG Xuefan.A new brushless doubly-fed machine with a wound-rotor changing-pole winding[J].Proceedings of the CSEE,2003,23(6):108-127.
[4] BRUNE C,SPEER,WALLACE A K.Experimental evaluation of a variable-speed,doubly-fed wind-power generation system[J].IEEE Transactions on Industry Applications,1994,30(3): 648-655.
[5] LIR,WALLACE A K,SPEE R,et al.Two-axismodel development of cage-rotor brushless doubly-fed machines[J].IEEE Transactions on Energy Conversion,1991,6(3):453-460.
[6] BOGER M S,WALLACE A K,SPEE R,et al.General pole numbermodel of the brushless doubly-fedmachine[J].IEEE Transactions on Industry Applications,1995,31(5):1022-1028.
[7] WILLIAMSON S,FERREIRA A C.Generalized theory of the brushless doubly-fed machine Part2:Model verification and performance[J].IEE Proceedings on Electric Power Applications,1997,144(2):123-129.
[8] FERREIRA A C,WILLIAMSON S.Iron loss and saturation in brushless doubly-fed machine[C]//IEEE Industry Applications Conference 32nd IASAnnual Meeting,Oct5-9,1997,New Orleans,USA.1997:97-103.
[9] 张凤阁,王凤翔,徐隆亚.磁阻和笼型转子无刷双馈电机的统一等效电路和转矩公式[J].中国电机工程学报,1999,19 (11):28-32. ZHANG Fengge,WANG Fengxiang,XU Longya.The equivalent circuit and torque formula of doubly-fed brushlessmachine with reluctance and cage rotor[J].Proceedings of the CSEE,1999,19 (11):28-32.
[10] 杨顺昌.无刷双馈调速电动机的数学模型[J].电工技术学报,1996,11(6):27-31. YANG Shunchang.Modeling of brushless doubly-fed machines for adjustable speed drives[J].Transactions of China Electrotechnical Society,1996,11(6):27-31.
[11] 杨向宇,励庆孚.无刷双馈调速电机的混合坐标数学模型[J].电工技术学报,2001,16(1):16-20. YANG Xiangyu,LI Qingfu.Hybrid reference frame model of brushless doubly-fed machines for adjustable speed drives[J]. Transactions of China Electrotechnical Society,2001,16(1):16 -20.
[12] 邓先明,姜建国,方荣惠.笼型转子无刷双馈电机的电磁分析和等效电路[J].电工技术学报,2005,20(9):19-23. DENG Xianming,JIANG Jianguo,FANG Ronghui.Electro-magnetic analysis and equivalent circuitof brushless doubly-fedmachine with cage rotor[J].Transactions of China Electrotechnical Society,2005,20(9):19-23.
[13] 王爱龙,熊光煜.无刷双馈电机时步有限元分析[J].中国电机工程学报,2008,28(21):123-127. WANG Ailong,XIONG Guangyu.Analysis of brushless doublyfed machine by time stepping finite element method[J].Proceedings of the CSEE,2008,28(21):123-127.
[14] 张凤阁,王凤翔,王正.不同转子结构无刷双馈电机稳定运行特性的对比研究实验[J].中国电机工程学报,2002,22(4): 52-55. ZHANG Fengge,WANG Fengxiang,WANG Zheng.Comparative experiment study on the performance of doubly-fed brushless machine with different rotor structures[J].Proceedings of the CSEE,2002,22(4):52-55.
[15] 辜承林.机电动力系统分析[M].武汉:华中理工大学出版社,1998:144-159.
(编辑:张诗阁)
D-q axismathematicalmodel of wound-rotor brushless doubly-fed machine
XIONG Fei1, WANG Xue-fan1, HUA Bin2, YIN Chuan-tao2
(1.State Key Laboratory of Advanced Electromagnetic Engineering and Technology,Huazhong University of Science and Technology,Wuhan 430074,China;2.712th Research Institute,CSIC,Wuhan 430064,China)
Based on the introduction of the statorwinding,rotorwinding structures andmathematicalmodel under a-b-c axis stationary reference frame ofwound-rotor brushless doubly-fed machine(BDFM),themathematicalmodel of themachine under d-q axis reference frame was proposed.Thismodel was built under arbitrary d-q axis reference frame and convenient for use,time-varying coefficientof themutual inductancematrices between statorwinding and rotorwindingwas eliminated,computational costwas reduced,facilitates future research on the control strategies,and studying and analyzing themachine performance in both dynamic and steady-state conditionswere applied.Themachine parameters can be calculated from the design geometry and empirical formula of the machine.Simulation analysis results and experimental datawere presented to show the validity of themathematicalmodel under arbitrary d-q axis reference frame.The establishment of themathematicalmodel under arbitrary d-q axis reference frame provides the foundation for the study of the performance analysis and control strategy of themachine.
brushless doubly-fed machine;mathematical model;wound rotor;d-q reference frame; simulation analysis
10.15938/j.emc.2015.05.012
TM 301.3
A
1007-449X(2015)05-0081-09
2010-12-10
国家科技支撑计划(2012BAG03B01);国家自然科学基金项目(51207061)
熊 飞(1983—),男,博士,讲师,研究方向为无刷双馈电机的运行理论与设计方法;
王雪帆(1954—),男,博士,教授,研究方向为新型特种电机及其控制;
华 斌(1977—),男,博士,高级工程师,研究方向为电力电子与电力传动;
尹传涛(1983—),男,硕士,工程师,研究方向为电力电子与电力传动。
熊 飞

