改进模型参考自适应控制及其在解耦控制中的应用

李杰， 齐晓慧， 刘新海， 汤子鑫， 韩帅涛

(1.军械工程学院无人机工程系，河北 石家庄 050003 2.总装备部南京军事代表局驻福州地区军事代表室，福建 福州 350000;3.解放军63880部队，河南 洛阳 471000)

改进模型参考自适应控制及其在解耦控制中的应用

李杰1， 齐晓慧1， 刘新海1， 汤子鑫2， 韩帅涛3

(1.军械工程学院无人机工程系，河北 石家庄 050003 2.总装备部南京军事代表局驻福州地区军事代表室，福建 福州 350000;3.解放军63880部队，河南 洛阳 471000)

提出了一种基于扩张状态观测器(extended state observer，ESO)的任意参考模型自适应控制方法，解决了被控对象状态信息不可测以及存在不确定因素导致模型参考自适应控制(model reference adaptive control，MRAC)效果变差甚至使系统不稳定的问题。在简述ESO数学模型的基础上提出了基于ESO的模型参考自适应控制方法并进行了严格的稳定性分析，仿真结果表明所设计方法具有跟踪速度快、稳态误差小、控制量小以及参考模型容易选择等特点。然后，提出基于改进MRAC的解耦控制方法并应用于三输入三输出的四旋翼飞行器姿态控制系统解耦控制，仿真结果表明该解耦控制方法具有鲁棒性好的特点。该方法无需按照通常的做法设计神经网络对不确定因素导致的误差进行补偿，大大简化了控制器设计过程。

模型参考自适应控制;扩张状态观测器;解耦控制;四旋翼飞行器;姿态控制

0 引 言

针对因被控对象存在不确定性和外界干扰而难以控制的问题，人们提出了自适应控制理论。目前，有多种不同类型的自适应控制系统，如模型参考自适应控制系统、自校正控制系统、智能自适应控制系统及其他形式的自适应控制系统。但从理论研究成果和实际应用情况来看，应当首推模型参考自适应控制系统和自校正控制系统［1］。

采用可调系统的状态变量构成模型参考自适应控制律的设计方案，需要准确获得对象的全部状态信息，这对许多实际系统来说往往是不现实的，设计一个自适应观测器来估计对象的未知参数和状态是一种解决方案［2］。此外，许多文献［3-8］对输出反馈自适应进行了研究，以规避状态信息难以获得的问题，但输出反馈自适应在同等条件下要逊色于状态反馈自适应。

实际系统往往存在外界干扰和测量噪声，系统建模时还可能存在未建模动态，而基于稳定理论设计的自适应律严格地说只能保证理想系统的稳定。自适应控制系统是一个非线性系统，在设计模型参考自适应控制时，应当考虑简化模型、外扰和噪声对系统的影响，否则稳定性得不到保证，这就提出了模型参考自适应系统的鲁棒性问题［2］。为了克服系统存在未建模动态及外扰等不确定因素时自适应控制器性能降低甚至不稳定的不足，很多文献［9-13］利用神经网络可以逼近任意非线性映射的能力，对不确定因素导致的误差进行补偿，获得了较好的效果。但神经网络的设计往往较为复杂，不同的网络本身也存在一些不足，这增加了解决实际问题的难度［14-16］

中科院韩京清研究员设计的扩张状态观测器能同时估计对象的状态信息以及系统存在的未建模动态和外扰［17］。基此，提出基于扩张状态观测器的模型参考自适应控制，克服被控对象状态信息不可测以及存在不确定因素导致控制效果变差甚至不稳定的问题，尤其是无需按照通常的做法设计神经网络，大大简化了控制器设计过程。同时，只要ESO设计合适，参考模型在与被控对象同阶并满足期望的性能指标前提下几乎是可以任意选择的，无需考虑被控对象的结构，这为高阶尤其是非线性的高阶被控对象参考模型的选择提供了极大便利。此外，利用扩张状态观测器还能有效地解决多输入多输出系统的解藕控制问题，且较传统的动态逆方法具有独特优势，因为传统的动态逆方法对系统数学模型的准确性要求很高(亦即鲁棒性差)［18-20］，而利用扩张状态观测器解决这个问题具有简单、鲁棒性的特点。

本文在介绍ESO的数学模型的基础上提出了一种基于ESO的模型参考自适应控制方法并进行了稳定性分析，进而通过实例仿真对其控制效果进行验证分析;然后，提出基于ESO-MRAC解藕控制方法并应用于三输入三输出的四旋翼飞行器姿态控制，最后通过仿真与动态逆方法进行了对比。

1 扩张状态观测器的数学模型

设受未知外扰作用的非线性不确定对象为:

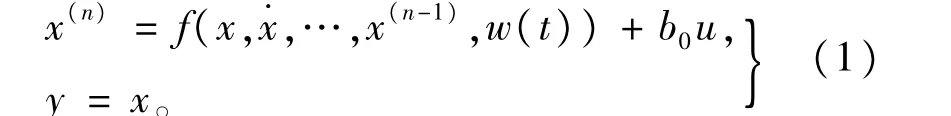
其中，w(t)未知外扰，f(x，x.，…，x(n-1)，w(t))(简写为f(.)，下同)为系统模型(包括已知模型部分和未建模动态)和外扰的总和，u及y分别为系统输入和输出，b0为已知常数。取上述对象的状态变量为x (t)，x.(t)，…x(n)(t)，假设f(.)是可微的且令h(x，w)=f′(.)，令xn+1(t)=f(.)称为系统的扩张状态变量，则系统扩张的状态方程为:

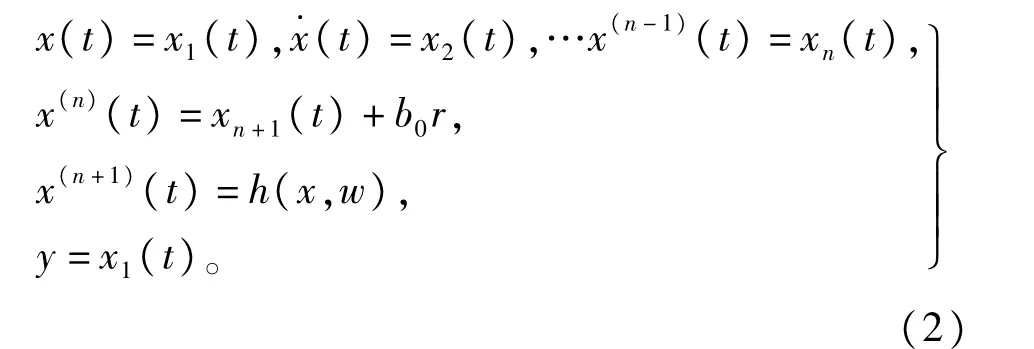
对这个扩张的系统可建立如式(3)所示线性状态观测器(LESO)，方程组如下:

其中，l1，l2，...，ln+1为待选取为正的常系数。这个系统能够很好地估计系统(2)的各状态变量以及被扩张状态变量，即xˆ1(t)→x1(t)，…，xˆn(t)→xn(t)，xˆn+1(t)→xn+1(t)=f(.)。有了这个被扩张状态xn+1(t)的估计值xˆn+1(t)，控制量可以取成u=u0-xˆn+1(t)/ b0，对象变成

美国克里夫兰州立大学高志强给出了用带宽确定LESO参数的简便方法［21］。考虑一特殊情况，选增益如下:

［l1l2…ln+1］=［ω0α1ω20α2…ωn+10αn+1］，(5)其中，ω0＞0，αi，i=1，2，…，n+1的选择要使特征多项式sn+1+α1sn+…+αns+αn+1满足劳斯判据。为简便，使sn+1+α1sn+…+αns+αn+1=(s+1)n+1，其中，。这样线性状态观测器的特征多项式变为:λ0=(s+ω0)n

并且观测器的带宽ω0成为了唯一可调参数。

2 基于ESO的模型参考自适应控制

2.1 基于ESO的模型参考自适应控制律设计

如图1为所设计的基于ESO的模型参考自适应控制器结构图。图中i=1，2，..，(n-1)，取［r1，。只要整定的扩张状态观测器参数合理，估计状态能很好地跟踪真实状态，理想状态下

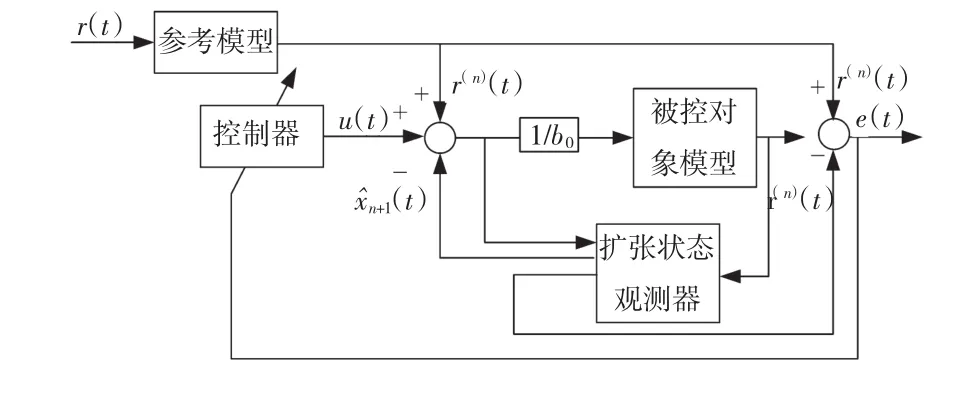
图1 基于ESO的模型参考自适应控制器结构图Fig.1 Block diagram of MRAC based on ESO

设被控对象形如式(1)所示，参考模型为:

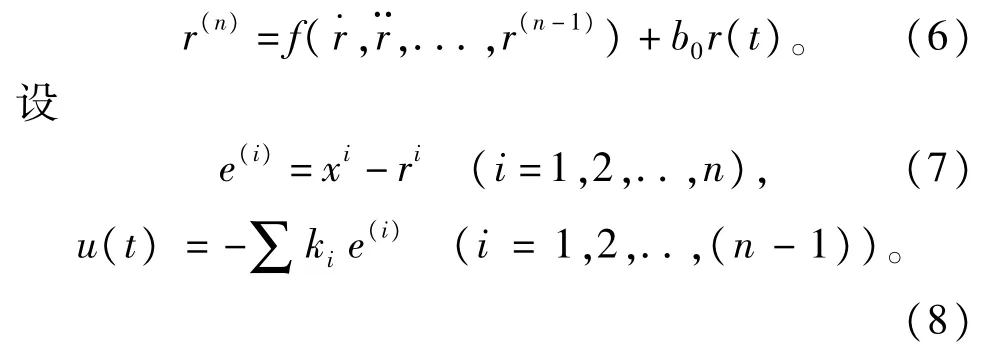
则被控对象输入

将式(9)代入式(10)，可得

进而可得

又根据假设条件

则可认为

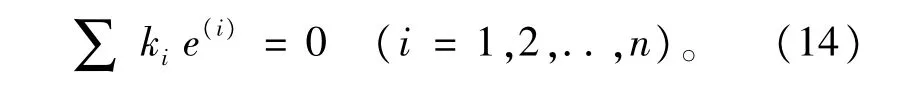
取系数ki(i=1，2，..，n)为定常数，对于这样一个高阶常系数齐次线性微分方程，其特征方程为

将式(16)右边展开，可解算得到ki(i=1，2，..，n)。考虑最简单的情况，即特征方程具有单负实根，则跟踪误差

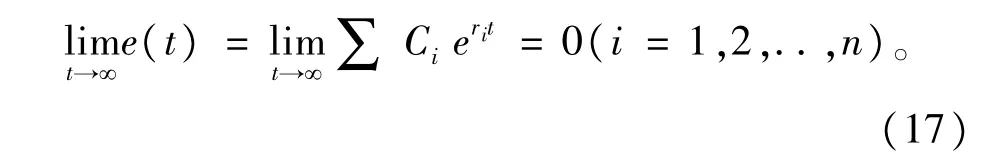
2.2 稳定性分析

文献［22-23］从不同理论角度分别证明了LESO在一大类干扰下的观测误差有界，给出了LESO稳定性的理论依据，文献［24］对非线性扩张状态观测器(NLESO)的收敛性进行了证明。结合这些成果，这里给出基于LESO的模型参考自适应控制系统稳定性的证明。证明分两步，第一步证明LESO的状态估计误差有界，第二步证明LESO的状态估计误差有界情况下系统是稳定的，跟踪误差是有界的。

2.2.1 证明LESO的状态估计误差有界

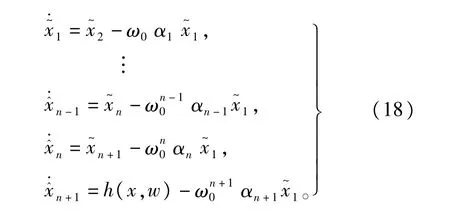
其中，

按照前述带宽概念确定的αi(i=1，2，…，n+1)使得矩阵A满足劳斯判据。

定理1 如果h(x，w)是有界的，那么存在一个常数σi和一个有限T1＞0，对于任意的t≥T1＞0和 ω0＞0，使得。其中，σi，k是正整数。

证明:解方程(19)得:

因为h(x(τ)，w)是有界的，即h(x(τ)，w)≤δ，其中，δ是一个正常数。这样，对于i=1，2，…，n+ 1，有

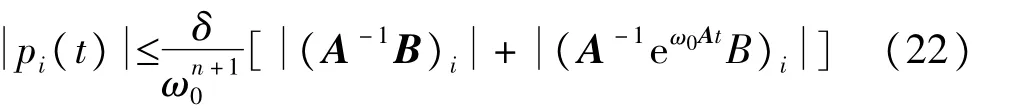
由式(19)中A和B的定义，得

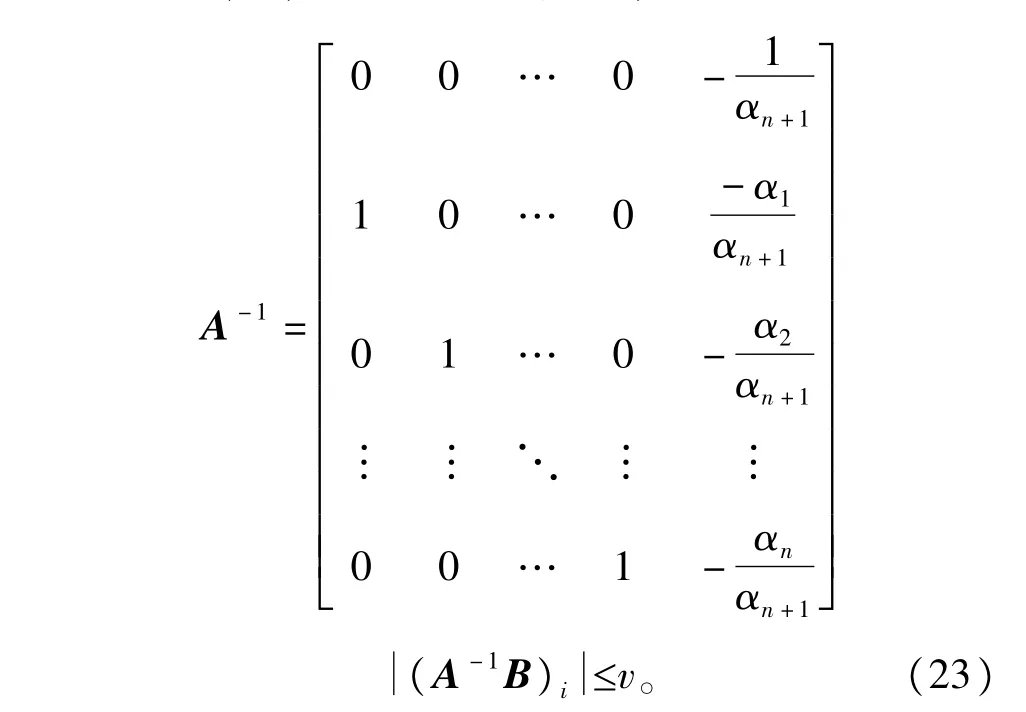
由于矩阵A满足劳斯判据，那么存在有限T1＞0，使得当t≥T1，i=1，2，…，n+1时，存在:

因此当t≥T1，i=1，2，…，n+1时，也存在:

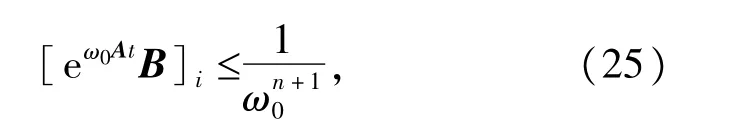
其中T1决定于

由式(22)、(23)和(26)可得，当t≥T1，i=1，2，…，n+1时有:可得

由式(20)得:

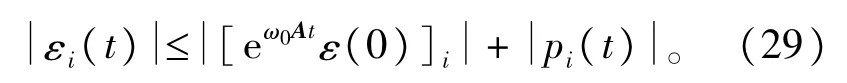
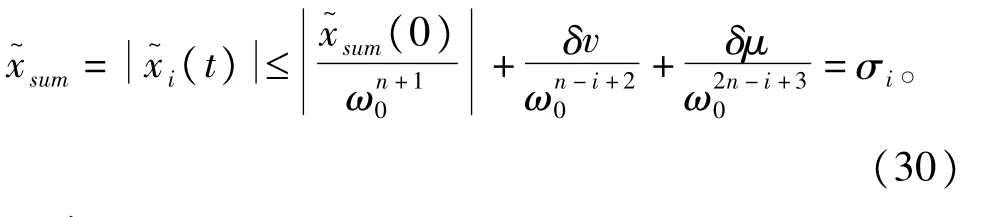
证毕。

如式(30)描述，LESO的估计误差是有界的，并且它的上界随着观测器带宽的增加单调递减。

2.2.2 证明系统稳定、跟踪误差有界

定理2 如果h(x，w)是有界的，存在一个常数pi＞0，和有限时间常数T2＞0，当∀t≥T2＞0，ω0＞0和ωc＞0时，使得。另外为正整数。

证明:由式(8)和(12)可得:

令ei=ri-xi，i=1，2，…，n，可得:

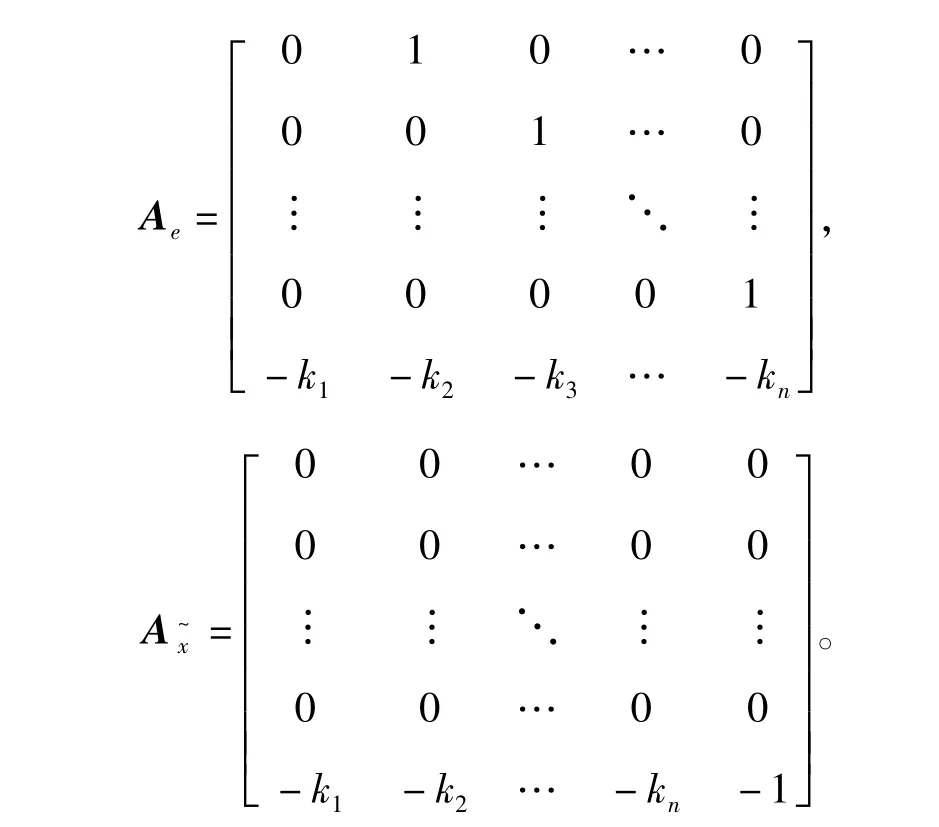
解式(33)得:

根据式(34)和定理1，得:

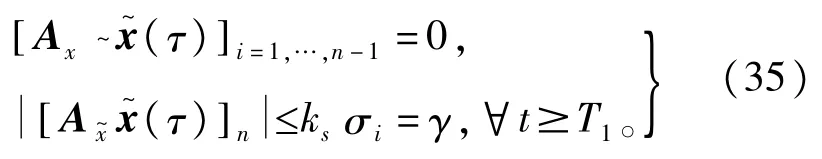
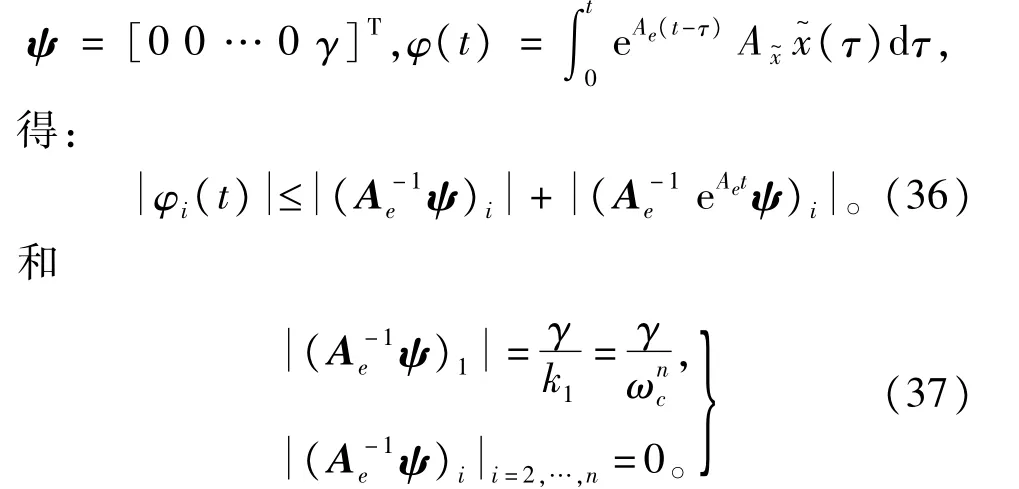
又由于Ae是满足劳斯判据的，因此存在一个有限时间常数T2＞0使得当t≥T2，i，j=1，2，…，n时有:

T2决定于Ae。取，则当t≥T3，i，j=1，2，…，n，有

进而有:

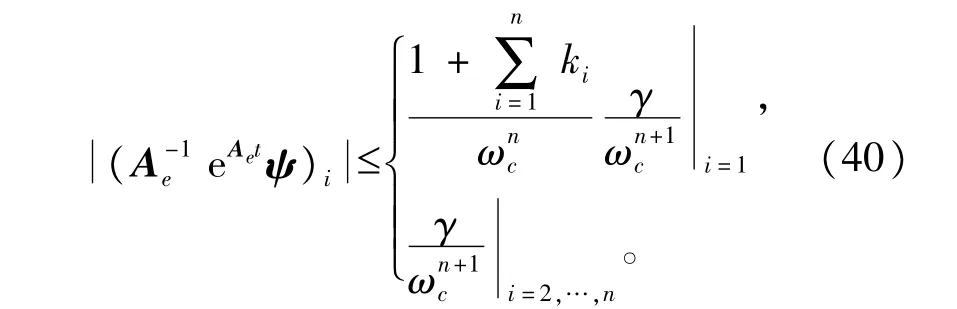
由式(36)、(37)和(40)得，当t≥T3时有:

由式(34)得:

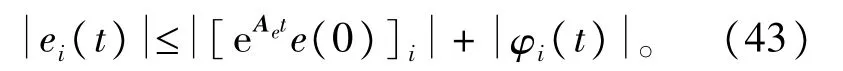
根据式(37)，(41)～(43)，得当t≥T3，i，j=1，2，…，n时有:

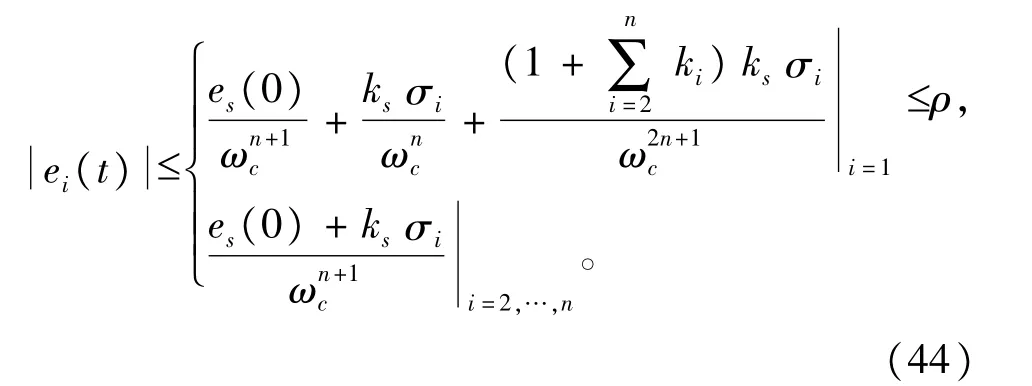
其中，

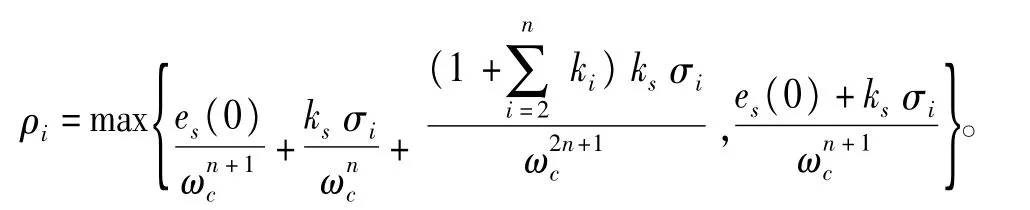
证毕。

如式(44)描述，基于LESO的闭环系统各状态对参考模型各状态跟踪误差是有界的，并且它的上界随着观测器带宽的增加单调递减。

而根据文献［24］的结论:基于NLESO的状态估计误差有界，结合第二步，可得到系统是稳定的、收敛是有界的。因此，无论采用LESO还是NLESO，只要能保证有界收敛，就能保证系统稳定、有界收敛。

2.3 实例仿真分析

设某二阶线性被控对象如式(45)所示

取二阶参考模型为

控制器参数设置:l1=40，l2=400，l3=800，k1=80，k2=250。对二阶系统而言，这个k1、k2有明确的物理意义，对应传统PID中的kd(微分)、kp(比例)。为体现本文所提方法优越性，考察单位阶跃响应，并依次与输出反馈自适应(无微分项，令kd=0)、无ESO补偿控制效果进行比较分析，且仿真对比过程中各项参数保持不变。仿真结果如图2～图7所示。

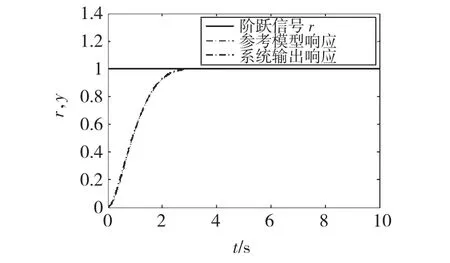
图2 基于ESO的模型参考自适应控制器阶跃响应Fig.2 Diagram of step response of MRAC based on ESO

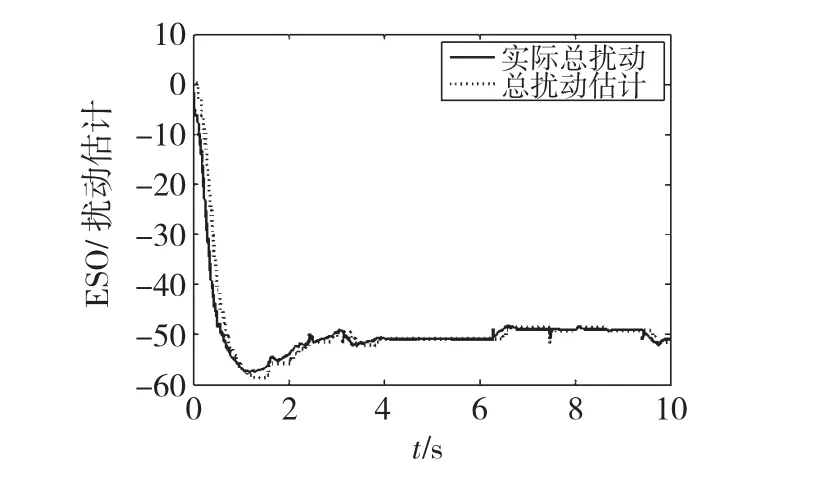
图3 ESO对系统模型和外扰总和的估计效果Fig.3 System“disturbance summation”and its estimation based on ESO

图4 ESO对系统状态的估计效果Fig.4 System states and their estimation based on ESO’

图5 状态反馈自适应和输出反馈自适应的跟踪误差Fig.5 Track error of adaptive control respectively based on state feedback and output feedback

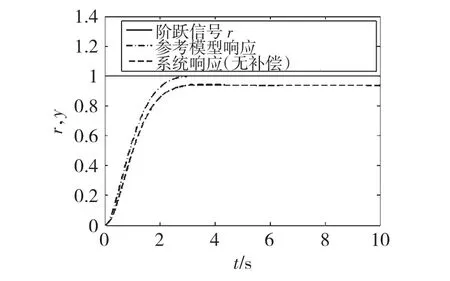
图6 无补偿的被控对象阶跃响应Fig.6 Diagram of step response w ithout com pensation

图7 有/无ESO的控制量Fig.7 control quantity w ith/w ithout ESO

由仿真结果图2可知，基于ESO的模型参考自适应控制能够使被控对象较好地跟踪参考模型输出，且具有如下优点:

1)由图3、图4可知，利用ESO可以进行状态估计，且由图5可知所设计方法较未采用状态估计的输出反馈自适应控制性能要好。从形式上看，输出反馈自适应只是P控制，而利用基于ESO进行状态估计利用了微分信息，实际上是PD控制，这也是较输出反馈自适应控制效果要好的原因。

2)由图6可知，利用扩张状态进行补偿，可以提高稳态精度。ESO既能抑制常值扰动，而且能够抑制消除几乎任意形式的扰动。虽然传统的靠误差积分反馈也能够抑制常值扰动，但常常使闭环系统的反应迟钝、容易产生振荡和控制量饱和等负作用。神经网络也能扰动估计、补偿，但设计复杂，且不具备状态观测器的功能。

3)由图7可知，由于ESO扩张状态的估计和补偿，使得控制作用大大减弱，这对工程应用有很大价值。

设某二阶非线性被控对象如式(47)所示

参考模型仍取式(17)所示，各项参数设置保持不变。仿真结果如图8、图9所示。

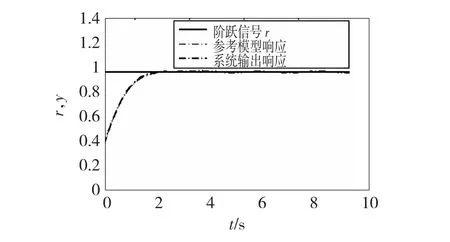
图8 基于ESO的模型参考自适应控制器阶跃响应Fig.8 Diagram of step response of MRAC based on ESO

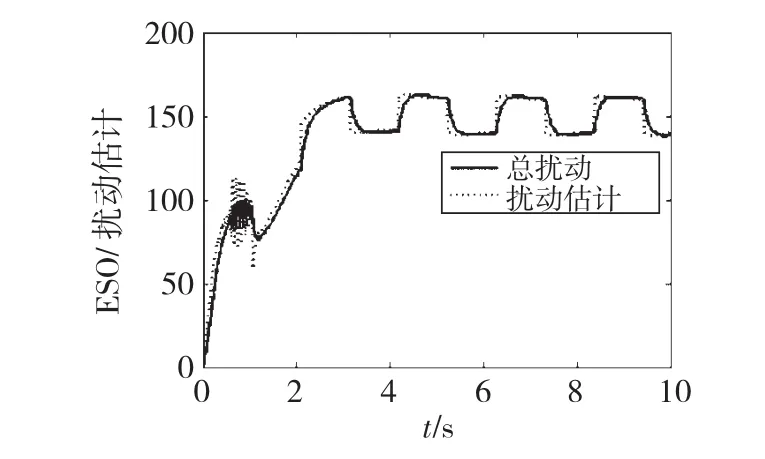
图9 ESO对系统模型和外扰总和的估计效果Fig.9 System“disturbance summation”and its estimation based on ESO

由图8、图9可知，尽管式(47)所示非线性被控对象与式(45)所示线性被控对象采用的均是同一参考模型，且参数设置保持不变，但依然能较好的跟踪参考模型的阶跃响应。其根本原因在于对于任意的被控对象(形如式(1))，由于a(t)=f(x，x.，…，x(n-1))+ω(t)的引入，转换为x(n)(t)=a(t)+b0r，只要a(t)能被很好地跟踪(扩张状态观测器参数设置合理即可)并进行补偿，对于对象模型、未建模动态以及内、外扰动都不再是选择参考模型需要特别考虑的。这就说明所设计控制器能移植于同阶被控对象的控制，也就降低了对选择参考模型的要求，这为高阶尤其是非线性的高阶被控对象参考模型的选择提供了极大便利。这都得益于ESO能对系统模型和扰动进行较好的估计，因此，只要设计一个合适的ESO，参考模型在保证具有期望的动态响应前提下几乎是可以任意选择的。另外，由于动态补偿线性化，整个系统工作于线性状态，规避了前面提到的自适应稳定鲁棒性问题。鲁棒性主要体现在ESO对“总和扰动”的估计上。

3 基于ESO-MRAC的多输入多输出系统解耦控制

多输入多输出系统的解藕控制方法无论是控制理论界还是控制工程界都是追求解决的重要问题。依靠系统模型的解决办法是有的，但是需要很大的计算量。利用ESO对扰动的估计和补偿可以解决好这个问题，所需计算量也不大，特别是控制器的鲁棒性很好。

3.1 解耦控制原理

为节省篇幅以及为后文仿真验证作铺垫，直接以三输入三输出的四旋翼飞行器姿态控制系统为例，介绍基于ESO的多输入多输出系统MRAC解藕控制方法。按照文献［25］小型四旋翼飞行器姿态非线性动力学模型，经过进一步整理得到如下形式:

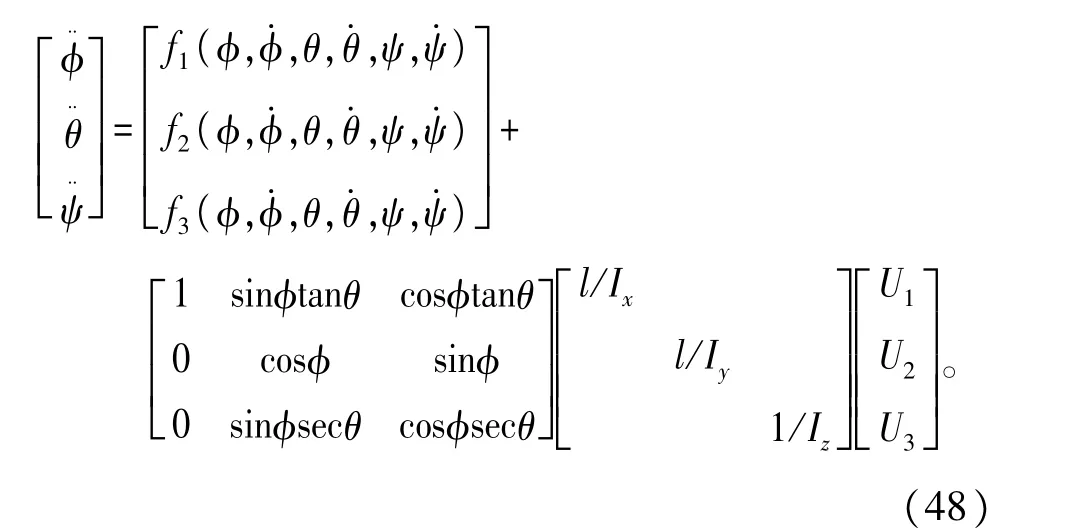
其中，

式(48)和式(49)中:p、q、r分别为机体角速度ω在机体坐标系三个坐标轴ox、oy、oz上的分量;φ、θ、ψ分别为滚转角、俯仰角、偏航角，l为螺旋桨中心至机体坐标系原点的距离;Ix、Iy、Iz分别为x、y、z轴上的惯性力矩;U1滚转输入控制量;U2俯仰控制输入量;U3偏航控制输入量;fi(i=1，2，3)为模型的藕合部分。

引入虚拟控制量Vi(i=1，2，3)及外扰ωi(t)(i=1，2，3)，设

可见，每个通道的虚拟控制量Vi与被控输出yi为单输入-单输出关系，即实现了Vi和yi之间的解藕。将模型“动态藕合”部分fi(.)及外扰wi(t)作为第i通道上的“扰动总和”，通过扩张状态观测器估计扰动量并加以补偿。这样，在控制向量V和输出向量y之间并行嵌入3个模型参考自适应控制器就能实现系统的解藕控制。这时，实际的控制量U=［U1U2U3］可由虚拟控制量V=［V1V2V3］得到，即U=B-1(φ，θ，ψ，t)V。

按照这一原理进行设计基于ESO的模型参考自适应姿态解藕控制器，结构如图10所示。

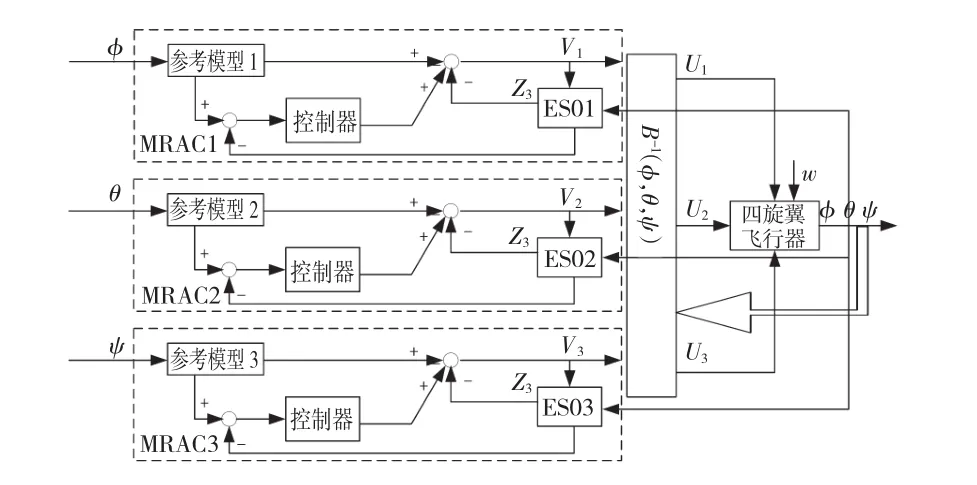
图10 基于ESO的四旋翼姿态系统MRAC解耦控制Fig.10 Schematic diagram of MRAC decoupling control based on ESO

以上以三输入三输出系统为例阐述基于ESO的解藕控制方法，可以推广到m输入m输出系统，只需要在形式(维数)上进行拓展。

3.2 仿真

由式(48)可知，每个通道都是二阶的，因此，仍可选择式(46)所示二阶参考模型。各物理参数:l= 0.198m，Ix=Iy=2.353×10-3kg.m2，Iz=5.562× 10-2kg.m2控制器参数设置:β1=20，β2=200，β3=600，k1=60，k2=200。为验证本文方法的解藕控制效果以及鲁棒性，对控制矩阵中惯性力矩Ix、Iy、Iz引入摄动+20%，并与基于动态逆解藕的模型参考自适应控制方法(不对不确定因素进行补偿)进行比较，初始状态姿态角φ=θ=ψ=0°，目标值θ=30°，φ=ψ=0°，俯仰通道仿真结果如图11所示。

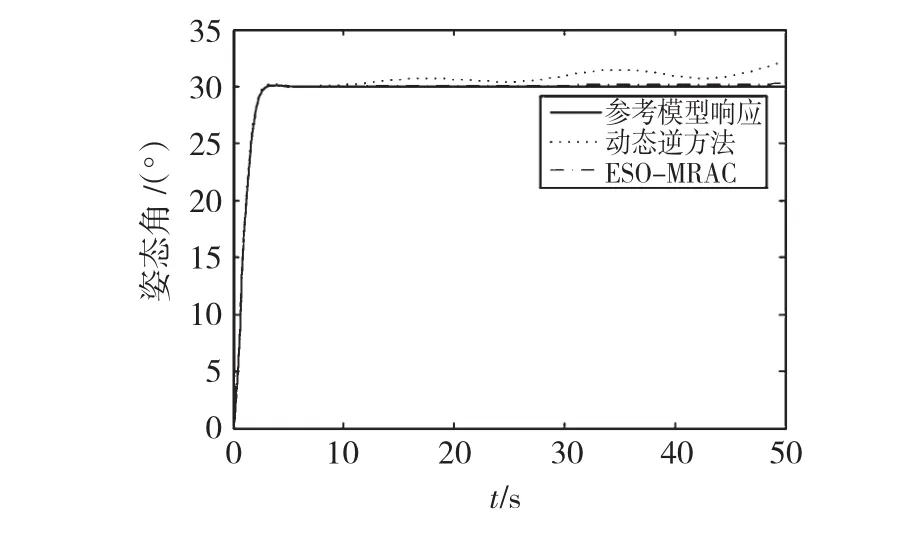
图11 俯仰通道解耦控制仿真结果Fig.11 Simulation result of decoupling control for pitching channel

由图11可知，在存在参数摄动情况下，基于动态逆解藕的模型参考自适应控制方法跟踪效果变差，有发散的趋势，而基于ESO的模型参考自适应姿态解藕控制方法依然能保持较好的控制效果，鲁棒性好。

4 结 论

本文提出了一种基于ESO的模型参考自适应控制方法，并进行了稳定性分析和仿真验证。在此基础上，进一步提出了基于ESO-MRAC的解藕控制方法，并应用于四旋翼飞行器姿态解藕控制中。理论及实例仿真分析表明本文方法不仅设计简单，还具有如下特点:

1)较输出反馈自适应控制性能要好;

2)利用扩张状态进行估计和补偿，提高了稳态精度;

3)控制作用大大减弱;

4)参考模型选择更加容易;

5)较动态逆方法解决多变量系统的解藕控制问题，具有简单、鲁棒性好的优点。

［1］ 庞中华，崔红.系统辨识与自适应控制MATLAB仿真［M］.北京:航空航天大学出版社，2009:5-8.

［2］ 董宁.自适应控制［M］.北京:北京理工大学出版社，2009: 98-100.

［3］ BECHLIOULISC P，ROVITHAKISG A.Robust adaptive control of feedback linearizable MIMO nonlinear systems with prescribed performanc［J］.IEEE Transactions on Automatic Control，2008，53(9):2090-2098.

［4］ YANG C G，ZHAI L F.Adaptive model reference control of a class ofMIMO discrete-time systemswith compensation of nonparametric uncertainty［C］//Proceedings of American Control Conferenc，June 11-13，2008，Seattle，USA.2008:4111-4116.

［5］ KIM N，CALISE A J.Neural network based adaptive output feedback augmentation of existing controllers［J］.Aerospace Science and Technology，2008，12(3):248-255.

［6］ HAYAKAWA T，HADDAD W M，HOVAKIMYAN N.Neural network adaptive control for a class of nonlinear uncertain dynamical sys-temswith asymptotic stability guarantees［J］.IEEE Transactions on Neural Networks，2008，19(1):80-89.

［7］ HOVAKIMYAN N，YANG B J，CALISE A J.Adaptive output feedback control methodology applicable to non-minimum phase nonlinear systems［J］.Automatic，2006，42(4):513-522.

［8］ HAGA R，MATSUURA A，SUZUKIS.Neural network based adaptive flight control using feedback error learning［C］//Proceedings of AIAA Guidance，Navigation，and Control Conference and Exhibit，August21-24，2006，Keystone，USA.2006:1-10.

［9］ YANG B J，CALISE A J.Adaptive control of a class of nonaffine systems using neural networks［J〛.IEEE Transactions on Neural Networks，2007，18(4):1149-1159.

［10］ SHIN Y，CALISE A J，MOTTER M A.Adaptive autopilot designs for an unmanned aerial vehicle［C］//AIAA Guidance，Navigation，and Control Conference and Exhibit，August 15-18，2005，San Francisco，USA.2005:1-20.

［11］ CALISE A J，LEE S，SHARMAM.Development of a reconfigurable flight control law for a tailless aircraft［J］.Journal of Guidance Control and Dynamics，2001，24(5):896-902.

［12］ HOVAKIMYAN N，YANG B J，CALISE A J.An adaptive output feedback controlmethodology for non-minimum phase systems［C］//Proceedings of the41st IEEE Conference on Decision and Control，December10-13，2002，Las Vegas，USA.2002:949 -955.

［13］ 李雪松，李颖晖，李霞，等.一种基于神经网络的任意模型参考自适应控制［J］.系统工程与电子技术，2011，33(1): 162-165. LIXuesong，LIYinghui，LIXia，et al.Arbitrary referencemodel-following adaptive control based on neural network［J］.Systems Engineering and Electronics，2011，33(1):162-165.

［14］ 段洪君，王凤文，史小平.飞行机器人递归小脑神经网络模型分解控制［J］.电机与控制学报，2011，15(1):92-97. DUAN Hongjun，WANG Fengwen，SHI Xiaoping.Recurrent CMACmodel decomposition control for flying robot［J］.Electric Machines and Control，2011，15(1):92-97.

［15］ 李雪松，李颖晖，阎晓鹏，等.基于边界值定量计算的神经网络自适应飞行控制［J］.西北工业大学学报，2011，29 (3):486-490. LIXuesong，LIYinghui，YAN Xiaopeng，et al.Design of an effective neural network(NN)adaptive flight control based on unmatched uncertain system［J］.Journal of Northwestern Polytechnical University，2011，29(3):486-490.

［16］ HAYAKAWA T，HADDAD W M，HOVAKIMYAN N.Neura lnetwork adaptive control for a class of nonlinear uncertain dynamical systems with asymptotic stability guarantees［J］.IEEE Transactions on Neural Networks，2008，9(1):80-89.

［17］ 韩京清.自抗扰控制技术——估计补偿不确定因素的控制技术［M］.北京:国防工业出版社，2008:183-242.

［18］ 蔡红明，昂海松，郑祥明.基于自适应逆的微型飞行器飞行控制系统［J］.南京航空航天大学学报，2011，43(2):137 -142. CAIHongming，ANG Haisong，ZHENG Xiangming.Flight control system of MAV based on adaptive dynamic inversion［J］. Journal of Nanjing University of Aeronautics&Astronautics，2011，43(2):137-142.

［19］ 刘芳，陈万春.应用Lyapunov方法分析自旋导弹动态逆控制器鲁棒性［J］.北京航空航天大学学报，2013，39(1):132 -137. LIU Fang，CHENWanchun.Spinningmissile dynamic inversion controller robustness analysis using Lyapunovmethods［J］.Journal of Beijing University of Aeronautics and Astronautics，2013，39(1):132-137.

［20］ 鲁可，袁锁中，刘曌，等.基于动态逆与QFT的鲁棒飞行控制器［J］.兵工自动化，2012，31(5):49-52. LU Ke，YUAN Suozhong，LIU Zhao，etal.Robust flight controller based on dynamic inversion and QFT［J］.Ordnance Industry Automation，2012，31(5):49-52.

［21］ GAO Zhiqiang.Scaling and bandwidth-parameteriz ation based controller tuning［C］//Proceedings of the 2003 American Control Conference，June 4-6，2003，Denver，USA.2003:4989 -4996.

［22］ DONGCHUL Y，STEPHENt S，YAU T.On Convergence of the linear extended state observer［C］//IEEE International Symposium on Intelligent Control，October 4-6，2006，Munich，Germany.2006:1645-1650.

［23］ YANG Xiaoxia，HUANG Yi.Capabilities of Extended State Observer for Estimating Uncertainties［C］//American Control Conference，June 10-12，2009，St.Louis，USA.2009:3700 -3705.

［24］ GUO Baozhu，ZHAO Zhiliang.On the convergence of an extended state observer for nonlinear systemswith uncertainty［J］.Systems&Control Letters，2011:420-430.

［25］ 黄溪流.一种四旋翼无人直升机飞行控制器的设计［D］.南京:南京理工大学自动化学院，2010:11-19.

(编辑:张诗阁)

Improved model reference adaptive control and its application in decoup led control

LIJie1， QIXiao-hui1， LIU Xin-hai1， TANG Zi-xin2，HAN Shuai-tao3
(1.Department of Unmanned Aerial Vehicle Engineering，Ordnance Engineering College，Shijiazhuang 050003，China; 2.General Equipment Department’s Military Representive at Fuzhou，Fuzhou 350000，China; 3.The PLA Unit 63880，Luoyang 471000，China)

An improved adaptive controlwith arbitrary referencemodewas presented based on the extended state observer(ESO)，focusing on solving the problems:(i)the system state is notmeasurable;(ii) themodel reference adaptive control(MRAC)is less effective or even make the system unstable when there exist internal or external uncertainties.After briefly describing themathematicalmodel of ESO，the improved MRAC was put forward and a strict stability analysiswas given.The simulation results show that the improved MRAC possesses quick tracking rate，high steady state accuracy and small controlmoment，including easily choosing a referencemodel.Then，a robust decoupling controlmethod based on the improved MRAC was proposed and applied to decoupling control of the attitude control for the quadrotor aircraftwith three inputs and three outputs.The simulation result shows that it has strong robustness.It is not necessary to design a neural network as usual to compensate for the uncertainties，which greatly simplified the process of controller design.

model reference adaptive control;extended state observer;decoupling control;quadrotor aircraft;attitude control

10.15938/j.emc.2015.05.016

TP 13;V 249

A

1007-449X(2015)05-0112-09

2013-12-02

总装创新工程项目;预研基金项目

李 杰(1988—)，男，博士研究生，研究方向为自抗扰控制、飞行器控制;

齐晓慧(1962—)，女，教授，博士生导师，研究方向为飞行器控制理论与应用;

刘新海(1987—)，男，讲师，研究方向为装备测试验证与评估;

汤子鑫(1987—)，男，助理工程师，研究方向为雷达工程、弹药工程;

韩帅涛(1988—)，男，助理工程师，研究方向为飞行器控制、电磁兼容。

李 杰