基于伪随机数加密的保护位置隐私近邻查询方法

张 峰，倪巍伟

（东南大学 计算机科学与工程学院，南京 211189；东南大学 计算机网络与信息集成教育部重点实验室，南京 211189）

1 引 言

空间定位与移动通信技术的发展促进了位置服务（LBS，location based service）的普及，人们能够方便地享受关于自身位置的一些近邻查询服务，诸如查找“距我最近的餐厅”，“我附近最近的几个加油站”等［1］．然而，位置服务需要查询者向服务提供方共享其位置信息，存在隐私泄露风险，包括位置服务提供商在内的潜在攻击者可以利用用户位置和查询内容鉴别查询者身份，进而获取其隐私信息．保护位置隐私需要，用户希望在不向服务提供方共享精确位置的同时获得位置服务．近年来，保护位置隐私近邻查询得到了研究者的持续关注．

目前，保护位置隐私近邻查询主要采用空间混淆［2－6］、数据变换［7－8］、假位置扰动［9－11］及隐私信息检索（PIR，Private Information Retrieval）技术［12－15］．空间混淆的原理是可信第三方接受查询者查询请求并将查询者位置隐藏为泛化区域，之后将隐藏后位置及查询请求提交LBS服务器处理，服务器将关于泛化区域的查询结果反馈可信第三方筛选出目标结果并返回查询者．该技术主要缺点是可信第三方易成为系统瓶颈、服务器端处理较复杂．假位置扰动采用发起一系列关于假位置的查询，查询者通过分析假位置、查询结果与真实位置的几何位置关系，筛选目标结果，存在保护强度不足以及假位置选择困难等问题．数据变换技术将查询者位置及POI坐标映射到另一个数据空间，实现保护位置隐私查询．该技术主要存在查询准确性较低的缺陷．

相较上述三种技术，PIR技术能够提供更高的位置隐私保护强度［13］．不同于传统位置隐私保护技术多数致力于客户端和服务器通信安全的保护，PIR还关注服务器端的安全，用户可以检索一个不可信的服务器上的任意数据项而无需暴露用户检索的数据项信息．目前所采用的PIR技术多数基于计算能力，即假设攻击者不具有计算求解某个难题的能力而保证用户对感兴趣数据的私密访问．尽管PIR技术具有隐私保护强度高、无需可信第三方以及查询结果准确的特点．但现有基于该技术的查询方法多数存在预处理时间长、查询效率较低的不足：

（1）基于PIR的查询方法通常针对所定义的攻击模式，制定查询计划，导致预处理时间增加，且服务器端POI一旦发生改变，查询计划也需修改，动态性较差．

（2）保护位置隐私查询通常生成一个包含真实查询结果的候选集．现有基于PIR的算法多数侧重减小候选集规模，而忽略候选集的生成效率．此外，在POI的存储组织上，多以单元格为基本单位，容易造成数据块中出现大量假POI，浪费储存空间．

针对上述问题，提出一种基于隐私信息检索的保护位置隐私近邻查询方法PRN＿kNN（Pseudo－random number encryption based privacy－preserving kNN query），通过引入Hilbert曲线编码，使用户可以在本地快速生成k近邻候选集；同时，引入伪随机数加密规则替代传统方法中查询计划，克服预处理时间长以及查询计划动态性差的不足，达到抵御模式攻击和增强位置保护强度的效果．

论文主要贡献包括：

（1）提出了一种基于隐私信息检索的保护位置隐私近邻查询方法PRN＿kNN，引入伪随机数加密规则替代传统方法中查询计划，克服预处理时间长及查询计划动态性差的缺点；

（2）利用Hilbert曲线加密原空间并连续组织存储POI实体，实现k近邻候选集生成的本地化和快速化；

（3）在真实数据集上对所提方法进行实验分析，验证所提方法的有效性．

论文组织结构如下：第二章对相关工作进行概述；第三章进行问题描述并介绍相关概念；第四章给出基于伪随机数加密规则的PRN＿kNN算法，并结合实例对算法进行分析；第五章对所提方法进行实验分析，验证其有效性；最后，总结全文并展望下一步工作．

2 相关工作

近年来，位置服务领域研究者针对保护位置隐私查询场景，提出了一系列位置隐私保护方法．主要包括空间混淆，数据变换，假位置扰动，隐私信息检索等．

2．1 常见位置隐私保护方法

空间混淆技术将查询用户位置提交可信第三方匿名服务器处理，生成包含用户位置的匿名区域代替查询者精确位置提交LBS服务器进行查询处理．例如文［2］提出了基于k匿名的空间混淆机制，将传统隐私保护数据发布领域的k匿名模型应用于位置服务中位置隐私保护．文［4］提出了CliqueCloak方法，支持个性化的隐私保护参数k；文［3］对在支持个性化隐私参数k基础上，提出支持用户自定义混淆区域规模的Casper方法．文［6］在匿名区域中，引入假用户协作机制．基于空间混淆的保护位置隐私查询机制往往依赖可信第三方服务器的位置匿名处理，可信第三方服务器容易成为系统性能和安全的瓶颈．

数据变换技术原理是将查询者位置及POI坐标转换到另一个数据空间，要求数据转换方法能尽可能保持原数据空间数据对象间的几何位置关系，以保证查询服务的准确性．文［7］介绍了多种不可逆数据变换方法，例如基于POI位置关系的加密方法和基于网格技术的映射；文［8］提出了基于Hilbert编码的保护位置隐私近邻查询机制，将二维位置坐标映射到一维Hilbert空间，借助Hilbert曲线参数实现位置隐私保护．其优点是不依赖可信第三方，且具有较高的位置隐藏与查询处理效率，但多数数据变换难以严格保证变换前后数据空间任意对象间几何关系的不改变，往往难以获取准确查询结果，为了提高查询结果的准确度，通常需要设计额外的处理机制，导致处理复杂度的增加．

假位置扰动采用假位置代替查询者真实位置，查询者不断向LBS服务器发起关于所选假位置的紧邻查询请求，并根据服务器反馈的查询结果与自身真实位置的约束关系，判断所返回结果是否为真实查询结果．例如文［9］提出基于假位置扰动的保护位置隐私近邻查询方法SpaceTwist；文［11］进一步提出基于中心服务器的改进方法，使得SpaceTwist满足k匿名约束．假位置扰动方法依赖于不可预知轮次的假位置迭代查询，存在隐私强度难以控制、且保护强度偏弱的缺陷，攻击者通过分析所选取假位置及查询中间结果能够将查询者位置锁定在较小的目标区域内，存在隐私泄露风险．

基于上述三种技术分别存在依赖可信第三方，准确性不足和隐私保护强度偏弱的缺点，近年来，基于隐私信息检索的技术得到研究者的持续关注，基于PIR的隐私保护方法具有强度高，不依赖可信第三方以及高准确性查询的特点［16］．

2．2 基于PIR的位置隐私保护方法

现有的PIR技术多数基于二次同余问题．二次同余问题的难度与因子分解难度相当［12］．用户向内置于服务器端的安全硬件［17］发出PIR请求，安全硬件指定查询向量，其中仅含有一个非二次同余数，利用二次同余性质，通过判断返回的数是否为二次同余，确定查询位为0或1，该方法同样适用检索POI存储块（POI块长固定）［14］．

文［12］证明了隐私信息检索能够有效保护用户隐私不泄漏．文［13］提出三种索引结构，并据此提出三种基于PIR隐私检索方法，其中两种存在区域划分和层次建立预处理时长不足，亦难以抵制模式攻击的缺陷．文［14］采用kd－tree和R－tree数据结构实现最近邻近似查询，利用Voronoi多边形完成精确最近邻查询，但存在准确性不足及多边形分割预处理代价大的缺陷，同时也只能处理最近邻查询．针对上述问题，文［15］引入查询计划机制抵御模式攻击，使得被不同频次访问的POI不易被区分，但依旧存在以下问题：（1）查询计划要求不同用户对数据库的访问次数相同，需要对访问次数进行预计算，而POI位置一旦改变，预计算结果将失效，存在动态性差的不足；（2）数据库中POI的存储以地图的单元格为基本单位，对相对稀疏的区域，需要大量假POI填充数据块，增加了无效检索的开销；（3）采用CPM算法［18］生成候选解集，该算法实现了访问最少的单元格生成候选解集，但存在确定待访问单元格的时间代价太大的问题，影响查询处理效率．

3 问题描述与相关概念

3．1 问题描述

前已述及，现有的基于PIR的保护位置隐私查询方法多数存在预处理时间长、候选解集生成效率低等不足．例如，文［13］提出方法存在区域划分与层次建立预处理时间长问题；文［15］提出的BNC＿kNN（Benchmark PIR based kNN query）方法，引入查询计划使得用户按相同次数访问数据库，导致预处理时间急剧增加．

基于PIR的保护位置隐私近邻查询方法需解决以下问题：

（1）查询预处理阶段，能够在兼顾隐私安全前提下，减少预处理时间；

（2）用户可以在本地通过PIR请求快速生成候选解集．

（3）能够防止攻击者借助不同用户访问数据库的频次特征发起的模式攻击．

3．2 相关概念

现有基于PIR隐私检索方法在预处理阶段存在时间较长不足．对给定k近邻查询，假设查询者Q1和Q2访问数据库的次数分别为cnt1、cnt2．当cnt1不等于cnt2时，攻击者根据截获查询者向服务器发出的查询请求频次，能够以一定概率确定查询者下次要查询的POI，甚至能够定位查询者，这种攻击方式称为模式攻击．针对模式攻击问题，文［15］引入查询计划，使得用户按相同次数访问数据库．BNC＿kNN算法对k近邻查询给定统一的访问数据库次数，使得攻击者不能区分查询者．但预处理阶段生成查询计划相当耗时，且不支持动态查询．文献［13］提出的两种检索技术同样存在预处理耗时大的问题．

伪随机数是随机生成的排列数序列，伪随机数加密规则能够起到模糊和加密查询的效果，同样可以重排和加密数据库．考虑引入了伪随机数规则加密数据库和相应查询，达到无法辨别查询内容、保护查询者的目的，即使查询次数不一样，由于不能确定推断查询者和查询内容，同样可以抵御模式攻击；此外，伪随机数的生成还具有参数单一，流程相对简单等特点．

定义1伪随机数加密规则．对于有n个元素的数据库DB，按规则π将DB转换成DBπ：DBπ［i］＝DB［π［i］］，规则π为1，2，…，n的一个全排列表示，又称伪随机数重排规则．

例如，对于数据库DB＝｛O1，O2，O3｝，n＝3，如果伪随机数规则π是｛2，3，1｝，则DBπ［1］＝DB［π［1］］＝DB［2］＝O2，DBπ［2］＝DB［π［2］］＝DB［3］＝O3，DBπ［3］＝DB［π［3］］＝DB［1］＝O1．因此，DBπ＝｛O2，O3，O1｝．假设符号PIR（id）表示要查询的POI实体的标志符．用户要查询O1，则id＝1，利用π规则加密id为3．因此向服务器提交PIR（3）（即采用PIR检索方法向用同样规则加密了的数据库查询标志符为3的POI）．

能否快速生成候选解集直接影响查询效率，文［13］采用闭包增长，层次查询以及希尔伯特区域查询生成候选解集，前两者效率不及CPM［18］，尽管希尔伯特区域查询可以快速确定候选集，却因需要提交整个候选解集矩阵闭包，使得定位k近邻重复了相当多的无用查询．文［15］执行算法CPM，能满足候选解集的规模最小，却以生成候选解集的时间消耗为代价，使得查询效率低下．为了解决这一问题，考虑利用Hilbert曲线保留近似邻接的性质，设置HPT以及NPT两张表，分别存储经SDK译码后POI的Hilbert值及每个单元格中POI编码信息．

定义2 Hilbert编码．二维平面下的Hilbert曲线记为HN2，其参数为SDK（X0，Y0，θ，N，ξ）．其中（X0，Y0）表示曲线的起点坐标；θ表示曲线的走势方向；N表示曲线的阶；ξ表示曲线的规模因子（0≤ξ≤22N－1）．

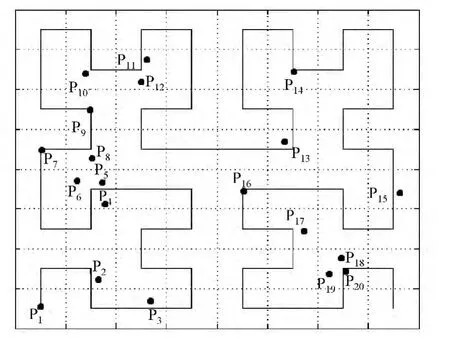
图1 Hilbert曲线加密的空间Fig．1 The encrypted space with Hilbert curve

图1描述了经Hilbert曲线编码后的某数据区域，数据区域规模为8＊8，包含20个POI．假设X0＝P1．x，Y0＝P1．y，N＝3，通过θ规定曲线顺时针走势以及ξ定义其规模为22N－1．表1、表2分别为HPT和NPT的表结构，分别存储经Hilbert曲线加密的POI以及单元格．图1中20个POI加密后值为：H（P1）＝0，H（P2）＝2，…，H（P20）＝61．

表1 HPT表结构示意Tab．1 The structure of HPT

表2 NPT表结构示意Tab．2 The structure of NPT

HPT以及NPT表以B＋树形式组织，用户Q查询k近邻时，首先计算出其当前位置的Hilbert值H（Q），根据Hilbert曲线的近似邻接性质，可以快速找到Q的k近邻候选集．查询者通过向安全硬件发起PIR请求，服务器做出对数据库中POI的访问，尽管数据库的组织对用户是透明的，但PIR查询却依赖其组织形式．文［15］中采用行列确定的单元格为基本单位储存POI，当数据块不够储存时，将多出的POI插在末尾，而当数据库块未填满时，采用假POI代替，将导致一些块包含大量假POI，增大了平均检索数据库次数．文［13］提出基于POI记录长度阈值λ的分割存储方法，解决POI实体记录不等长带来的空间浪费问题，提高了空间利用率，然而需要遍历所有POI实体并计算其长度以便进行分割存储处理，存在预处理耗时较大问题．本文所提算法考虑不以单元格为基本存储单位，对原空间中POI进行Hilbert编码加密后，按Hilbert编码值依次存入数据库DB1和DB2，前者存储查询内容的索引，后者用于存储查询内容．DB1和DB2的块大小与结构沿用文［15］所采用结构，DB1存储的POI实体结构为＜P·id，P·x，P·y，P·ptr＞，分别对应POI的标志符、平面坐标、指向DB2中存储该POI详细信息的索引；DB2中存储POI实体相关信息结构＜P·id，P·tail＞，P·tail为该POI的详细信息．例如在某次最近邻Pr（id＝r）查询中，用户通过客户端向服务器发出隐私检索请求PIR（r），安全硬件对数据库DB1进行检索，取得指向DB2中存有点Pr的详细信息（也是用户所要查询的信息）的块地址Pr·ptr，然后，安全硬件利用该地址对DB2相应块隐私检索并将包含所要查询的信息Pr·tail的POI返回给用户．不同之处在于本文所提方法将POI经伪随机数加密后，逐一放入块中，而不以地图单元格为块存储单位．

定义3强隐私保护系统．给定一个kNN查询系统，攻击者在不破解安全硬件和伪随机数规则两个条件下，推断这k个POI的概率小于等于其中n为POI的全部数目．称该系统为强隐私保护系统．

首先采用伪随机数规则对用户查询请求进行加密，并将加密后查询请求提交安全硬件，安全硬件接受用户的查询请求，并对数据库进行隐私信息检索，隐私信息检索过程本身具有高隐私保护强度，又经过伪随机规则处理，双重保护下查询机制将具有更强的隐私保护强度．

4 保护位置隐私近邻查询方法PRN＿kNN

4．1 基本思想

本文提出的PRN＿kNN方法通过引入Hilbert曲线加密原二维平面中的POI实体，使得用户可以在本地快速查询k近邻的候选解集，候选解集包含真实的k近邻的标志符．在此基础上，引入伪随机数加密规则替代传统方法中查询计划，克服了查询机制预处理时间长以及查询计划的动态性差的缺点，同时达到抵御模式攻击和增强保护强度的效果．在POI存储组织方面，改进文［15］的数据存储结构，不再以单元格为基本存储单位，按照POI标志符顺序存储，以提高存储效率和平均检索盘块次数．

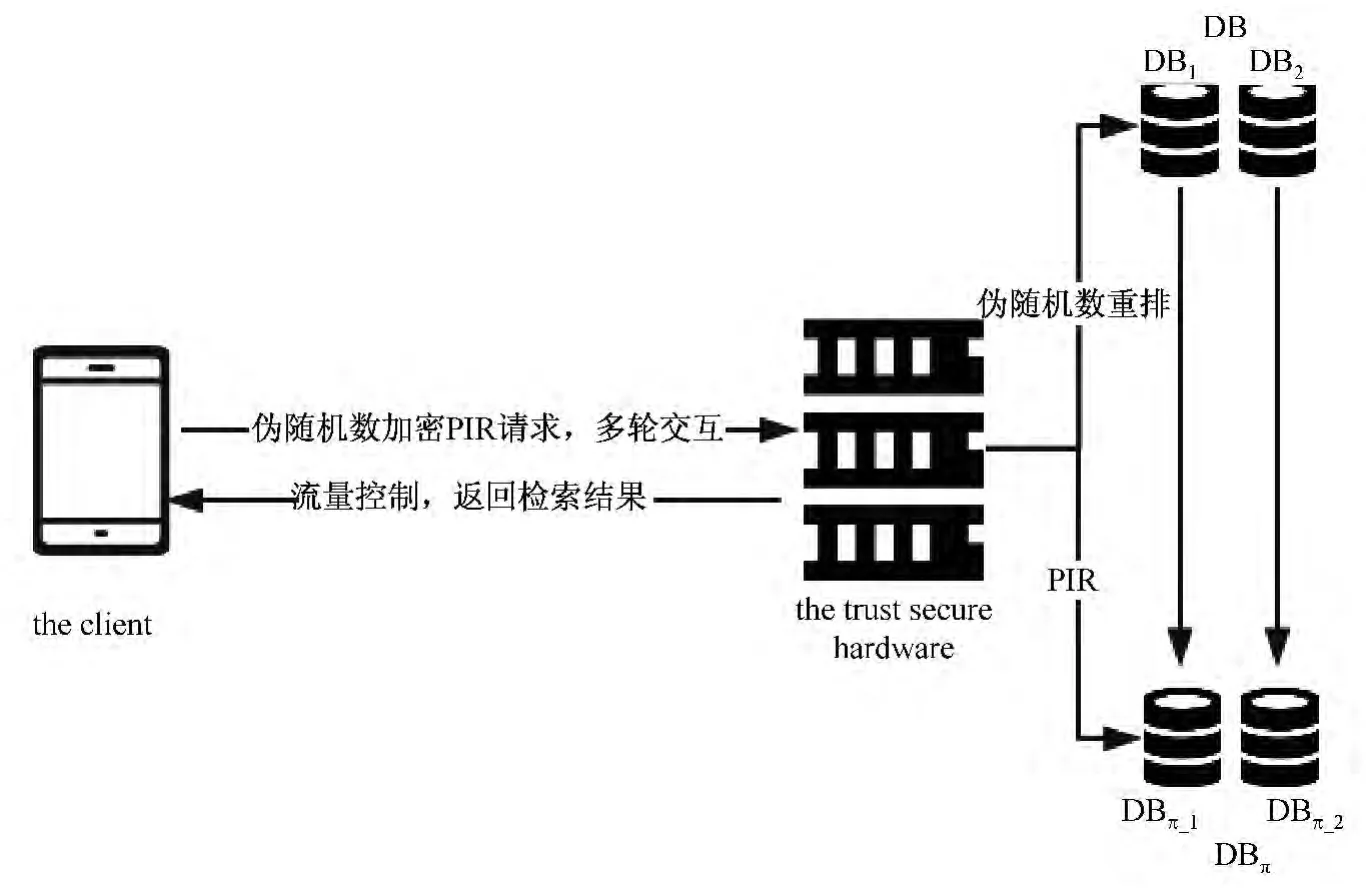
图2 系统流程Fig．2 The PRN－kNN system architecture

系统流程见图2，客户端向安全硬件发送PIR请求前，服务器先对存储POI的数据库DB利用规则π加密成DBπ．在查询阶段，安全硬件对数据库DBπ直接进行隐私检索，并将查询结果交付服务器，服务器将根据网络状况进行流量控制，返回查询客户端．

查询系统包含三部分：客户端，安全硬件，数据库．其中安全硬件机制由内置服务器端的硬件实现．整个查询过程可分为以下四步：

第1步：利用伪随机数规则加密数据库DB1，DB2；

第2步：对查询同样加密，并向安全硬件发出多轮PIR请求，获取候选解集；

第3步：根据候选解集中点距查询者的距离远近，确定查询者的k近邻；

第4步：利用kNN所在块的索引地址，向安全硬件发出多轮PIR请求，返回查询结果．

分析易知，整个查询过程，服务器端内置的安全硬件承担了主要工作．它负责执行PIR和加解密伪随机数规则．客户端并不要求高处理能力，它在了解数据库组织和伪随机数规则前提下，不断提出PIR请求，直至返回查询的内容．

4．2 模式攻击处理

模式攻击指攻击者借助所掌握不同用户访问数据库的不同频次，推断用户下一次检索目标的攻击方式．BNC＿kNN针对该问题提出了查询计划，要求用户按相同次数访问数据库，以保证攻击者不能根据访问频次差异去窥测用户隐私．PRN＿kNN克服了BNC＿kNN预处理时间长等问题，算法采用伪随机数加密规则对数据块中的实体加密重排，即便攻击者获得了各POI的访问频次，但这些POI是经过随机重排的，并不代表真实实体的频次，从而混淆查询，避免了模式攻击的发生．

伪随机数加密规则首先对数据块中的POI利用规则π随机重排，然后将其放入指定数据块中，生成了加密数据库DBπ．在用户查询阶段，客户端同样利用规则π对要查询的POI编号加密，发送给服务器，服务器端的安全硬件利用加密后的编号对数据库DBπ发出PIR请求，接收返回的数据后，直接返回给客户端．具体加密流程见算法1．

算法1伪随机数重排算法

输入：DB，原数据库记录，π加密规则

输出：DBπ加密后的数据库

1．entries＿DB＝φ；／／POI输入缓冲区

2．out＿DB＝φ；／／POI输出缓冲区

3．for each block bin DB

4．entries＿DB．push（b）；

5．if（entries＿DB！＝φ）

6．blockb1＝entries＿DB．pop（）；／／取出块

7．Integer index＝b1．blocknumber（）；／／index记录块号

8．for each POI Pin block b1

9．if（P！＝NULL）

10．entires P＝b1．pop（）；／／取出块内POI

11．DBπ［P·id］＝DB［π［P·id］］；／／加密POI

12．block temp．push（P）；

13．if（temp．isfull（））／／若块满加入输出缓冲区

14．out＿DB．push（temp）；

15．if（out＿DB！＝φ）

16．block b2＝out＿DB．pop（）；／／取输出缓冲区内块

17．DBπ．insert（index，b2）；／／加密后的块插入DBπ［index］位置

18．end if

19．end if

20．end if

21．end for

22．end if

23．end for

24．return DBπ；

以图1中数据集DB＝｛P1，P2，P3，P4，P5，…，P20｝为例，给定的排列规则π为［20，19，18，…，1］，利用DBπ［i］＝DB［π［i］］．可以得出DBπ＝｛P20，P19，P18，P17，P16，…，P1｝．按照这个规则可以加密数据库DB中所有块内的POI．然后DB按次序储存DBπ内的POI．得到B1，1＝｛P20｝，B1，4＝｛P17，P16，P15｝，B1，16＝｛P3，P2，P1｝；B2，1＝｛P20，P19，P18｝，B2，4＝｛P11，P10，P9｝，B2，7＝｛P2，P1｝．

4．3 候选解集生成

候选解集的生成直接影响查询效率，对于k近邻查询，用户通过在DB1上初步查询，生成大于等于k个近邻目标．这些POI构成候选解集，进一步的筛选距离最近的k个对象，再通过查找这些对象包含的索引信息，对DB2发出PIR请求，返回最终的查询结果．

客户端首先生成查询位置Q的Hilbert编码H（Q），然后从位置Q开始沿着加密曲线双向遍历单元格，利用NPT找出其内的POI，并向安全硬件发出PIR请求直到返回的POI数目大于等于k为止．整个生成过程如算法2所示．

算法2候选解集生成算法

输入：用户位置Q，DB1加密重排后的数据库DBπ＿1，查询目标数k

输出：S候选集

1．S＝φ；／／初始化候选集为空

2．WhileS．size＜k ／／候选集规模大小k

3．H－index h＝H（Q）；／／Q所在单元格的希尔伯特值

4．for int i＝0；；i＋＋

5．h±＝i；／／双向近邻搜索

6．if（h≤22N－1） ／／N表示地图G的粒度

7．Integer index＝NPT［h］；

8．for each POI Pin NPT［h］／／依次取出块内POI并入集合S

9．POI P＝PIR（P．π［index］）；

10．S．push（P）；／／POI入集合S

11．end for

12．end if

13．end for

14．end while

15．dist＿k＝distance fromQto its kth NN in entries＿DB1；／／利用第k近邻生成kNN候选集S

16．c＿set＝set of yet unseen cells overlapping with circleC（Q，dist＿k）；／／剩余未扫描的单元格

17．for each cell cin c＿set

18．对c内每一个POI P·id隐私检索PIR（id）并入S；

19．end for

20．return S；

仍以图1为例，假设用户所在位置Q和P7同一单元格，k＝3，已知H（Q）＝16，查找NPT，发现该单元格内仅有P7，将P7加进集合S．继续沿着曲线遍历编码值为17、15的单元格，对单元格内的POI进行PIR检索，将得到的P8添加进集合S．当遍历到编码值为18和14的单元格时，得到的P9也加入集合S．此外，S中正好包含3个POI，接着以Q为圆心，Q到P9的距离为半径作圆，交点有12，15，16，17，18，19，其中15，16，17，18已经访问过，只需搜索单元格12，19即可，将P4，P5，P6入S．算法返回S作为候选集，供进一步查询使用．

性质1候选集S中一定包含真实的kNN．

证 明 利用反证法，假设P∈kNN，同时满足P∉S，也就是真正kNN内一点P，不包含于集合S，P’是S内距离用户Q最远的POI，半径为R．因为P∉S，所以dist（Q，P）＞R，又因为P∈kNN，所以dist（Q，P）≤R，矛盾，所以，P不存在．原命题得证．

4．4 算法描述

算法PRN＿kNN需要由用户指定查询值k以及给定一个伪随机数规则π．算法分三步，第一步，调用算法1，对数据库中POI加密．第二步，调用候选集生成算法，产生候选集返回给客户端．第三步，客户端对候选集中的POI，根据到用户位置Q的距离，一般是欧几里得距离排序，保留前k个POI，这k个POI索引包含了DB2中含有这些POI的块．第四步，通过这k个POI中的P·ptr，确定DB2中相应块，再次PIR检索并将最终查询结果返回给客户端．

算法3 PRN（Q，k，π）

输入：查询者位置Q，近邻查询数目k，伪随机数规则π

输出：kNN查询信息

1．令entries＿DBπ＿1＝φ，entries＿DBπ＿2＝φ，kNN＝φ；／／分别表示DBπ＿1、DBπ＿2的缓冲容器

2．调用伪随机数重排算法加密DB1和DB2；／／生成加密重排后的数据库

3．调用候选集生成算法产生候选集entries＿DBπ＿1；

4．kNN＿DBπ＿1＝set of kNN result entries in entries＿DBπ＿1；／／取候选集前k个POI

5．for each POI Pin kNN＿DBπ＿1

6．if（P！＝NULL）

7．PIR（P·ptr）检索对应的DBπ＿2＿block并将块内实体入entries＿DBπ＿2；

8．end for

9．for each POI P1in kNN＿DBπ＿1

10．for each POI P2in entries＿DBπ＿2

11．if（P1·id＝P2·id）

12．Insert P2into kNN；／／将包含查询信息（tail）的P2入集合kNN

13．end if

14．end for

15．end for

16．return kNN；／／返回查询结果

PRN＿kNN算法中，第1—2行为第一阶段，第3行为第二阶段，第4行为第三阶段，第5—16行为第四阶段．下面结合图3给出示例，假设查询者发起2NN查询．

客户端沿着Hilbert曲线依次遍历Hilbert编码为H（Q），H（Q）±1，H（Q）±2，…的单元格，结合NPT以及HPT经PIR检索获得P8、P9两个近似的邻近POI．利用4．2给出的伪随机数加密规则确定它们在重排后的数据库中位置为P13、P12．再次利用NPT以及HPT，确定它们分别位于重排后的B1，10，B1，9，多轮PIR检索下面重排后DBπ＿1矩阵B1，10和B1，9．安全硬件利用π规则加密两块中的POI对象P13、P12，并反馈给客户端．如下图矩阵所示，左侧表示加密后的DB1，右侧表示加密后的DB2，安全硬件对加密后的数据库实现PIR访问，图中NaN表示数据库矩阵未满时，插入的空闲块．

图3 2NN查询Fig．3 The example of 2 nearest neighbers

客户端收到加密后的POI为P13、P12，解密获取原空间中的P8、P9．以Q为圆心，Q到P9的距离dist（Q，P9）为半径作圆，圆与地图区域所包含单元格的交点的Hilbert值为12、13、16、17、18、19、20、31．利用NPT以及HPT访问还未检索过的POI对象P4、P5、P6、P7，第一阶段对这四个点进行PIR访问，客户端在获取P4、P5、P6、P7、P8、P9六个点后，利用欧氏距离排序，得出实际的2NN为P8、P6．第三阶段，客户端向安全硬件发送加密后的P13、P15查询请求，安全硬件直接利用P·ptr确定上面给出的重排后的DBπ＿2矩阵中的块B2，5．PIR检索该块并返回，客户端收到解密信息，通过P8、P6的P·id连接B2，5中的POI对象P6、P7、P8，取得最终要求的P·tail．

4．5 算法分析

本节对PRN＿kNN算法的隐私保护强度以及算法时间复杂度进行分析．

在位置隐私保护方面，算法主要从三方面提供保证，安全硬件、Hilbert编码以及伪随机数加密．安全硬件提供对外PIR请求接口，对内的隐私检索数据库，安全强度高，Hilbert编码和伪随机数加密起到加密空间和重排POI效果，实现了多重隐私保护．

性质2基于PRN＿kNN方法的查询系统为强隐私保护系统．

证 明 由于k＜＜n，攻击者在客户端与服务器通信过程中截获查询请求，即使连续记录伪随机数加密后的POI编号，仍不能推断伪随机数加密规则，同时在安全硬件对数据库I／O过程中，满足基于计算的隐私信息检索原理．此外，数据块中的POI实体也经过加密处理，攻击者短时间内不能破解PIR请求．因此，对kNN查询，满足“独立同分布”查询性质，推断kNN查询概率小于等于

与传统的BNC＿kNN算法一样，PRN＿kNN除本地生成候选解集，筛选真实POI以及POI详细信息查询三阶段外，还需对加密数据库进行预处理．因为涉及所有POI的重排，所以时间复杂度为O（n），相较文［13］查询计划复杂度为O（n2）代价更低．PRN＿kNN满足轻客户端重服务器思想，本地客户端计算代价小，只需执行kNN算法以及利用伪随机数规则加解密发送和接受的POI，检索工作完全由内置于服务器端的安全硬件承担．文［8］给出采用希尔伯特曲线加密查询kNN时间复杂度为其中N表示曲线的阶数，n表示POI数量．PRN＿kNN预处理后的查询时间复杂度主要由三部分构成：生成候选集、排序候选集求出真实查询的POI以及检索数据库块．总的时间复杂度为空间复杂度在于常驻内存的NPT以及HPT两张表，规模为O（n）．

5 实验分析

5．1 实验环境

算法采用C＋＋11实现，计算机硬件配置如下：AMDPhenomIIN6603．0GHZ处理器、4GB内存，操作系统为Win7．实验数据来源于美国东北部邮局地点，数据集包含123K个POI．区域面积为106×106（数据经过规格化，不含单位），规格化后POI分布压缩如图4所示．

图4 真实数据集分布Fig．4 Real data set distribution

假设每个POI中tail属性占用1 KB，导致数据库大小为128 M．同时假设每个数据块大小为4 KB．我们采用模拟的安全硬件，利用二次同余以及伪随机数规则检索数据．实验模拟一个双工的网络通信信道，客户端带宽为1 Mbps，与LBS一次来回通信（round－trip－time）为10 ms．

5．2 实验结果分析

本节对PRN＿kNN以及基于PIR的经典保护位置隐私查询算法BNC＿kNN进行查询效率的对比分析（安全性方面两者采用相同的安全硬件机制，不同在于PRN＿kNN引入伪随机数规则替代BNC＿kNN所采用的查询计划，两算法均可避免模式攻击）．分别从地图G的粒度（granularity）选择、第一阶段候选集规模大小、访问DB1时长（候选解集生成时间）以及总的查询时长四个方面对比算法性能．

如图5所示，不同粒度会影响查询效率，因为粒度的不同，导致单元格内POI数量发生变化，同时导致数据库组织发生变化．图5（a）和（b）分别表示k＝1和k＝5时，不同粒度下查询总时长．粒度太小导致单元格数量急剧增加，数据库块数量跟着增加，I／O增加，时耗变长；粒度过大时，尽管单元格数量较少，但会使数据块中存储大量假POI实体，浪费空间，检索次数也增加．可以得出BNC＿kNN对粒度更加敏感，而PRN＿kNN则更为稳定．

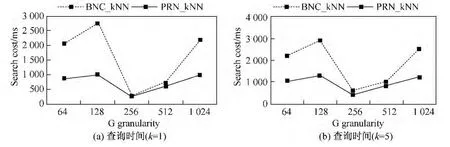
图5 粒度对查询效率影响Fig．5 Performance vs G granularity

实验发现，当粒度在256附近时，两算法查询效率均较高．公平起见，后续实验的粒度均取256．

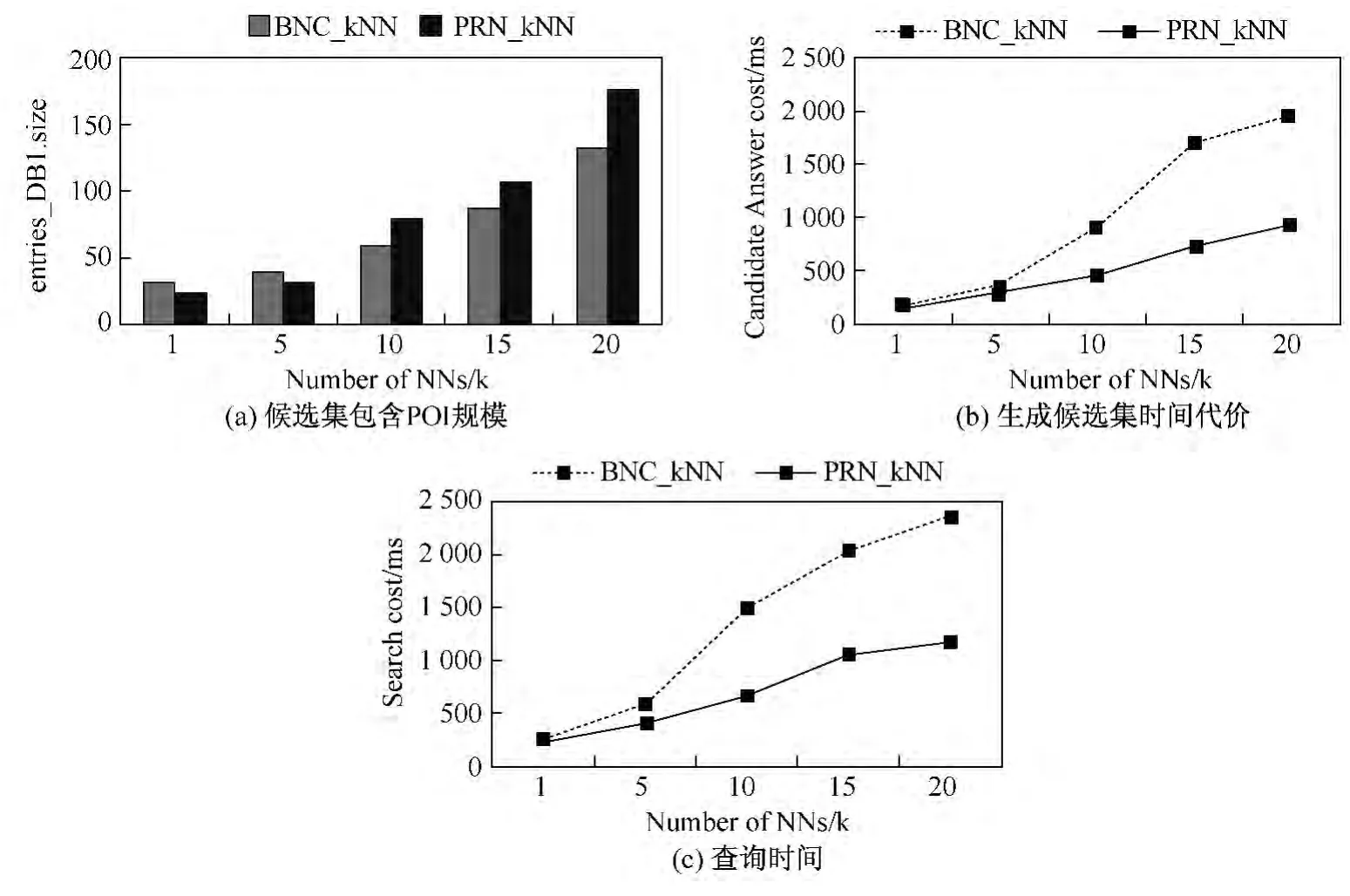
图6 候选集大小以及查询时长（granularity＝256）Fig．6 Candidate size and search cost

图6（a）表明随着k＝1到k＝20变化，PRN＿kNN得到候选解集规模始终比BNC＿kNN稍大，这是因为文［18］在理论证明CPM算法所需访问遍历的单元格最少．但是对DB1数据块的访问时长，PRN＿kNN更短，特别当k＞10时，差距更趋明显．因为CPM算法采用R树型结构存储块执行，需要采用回溯寻找最佳单元格，而PRN＿kNN算法中，沿着已经编码NPT索引实现检索，结构更加简单，速度更快．图6（b）表明PRN＿kNN算法尽管候选集规模比BNC＿kNN算法偏大，但其对数据库的检索效率明显更优．如图6（c）所示，随着k值增加，PRN＿kNN算法查询代价及代价增长幅度上均优于BNC＿kNN算法．

6 总结与展望

针对已有基于PIR的保护位置隐私近邻查询方法存在的查询效率等方面不足，提出了基于伪随机数的保护位置隐私k近邻查询方法PRN＿kNN，采用伪随机数重排数据库和查询请求，使得攻击者即便掌握数据库访问频次仍无法根据查询次数与受欢迎程度推断出目标POI，避免模式攻击，在此基础上，引入Hilbert曲线编码，使客户端快速实现候选解集的本地化生成．理论分析和实验结果验证了算法的有效性．PRN＿kNN算法尚未考虑网络通信现实情形，下一步将考虑基于PIR的保护位置隐私查询中流量控制及通信效率等问题．

［1］ROUSSOPOULOS N，KELLEY S，VINCENT F．Nearest neighbor queries［C］／／Proceedings of the ACM Special Interest Group on Management of Data（SIGMOD’95）．California，USA，1995：71－79．

［2］GRUTESER M，GRUNWAL D．Anonymous usage of location based services through spatial and temporal cloaking［C］／／Proceedings of the International Conference on Mobile Systems，Applications，and Services（MobiSys’03）．California，USA，2003：31－42．

［3］MOKBEL M F，CHOW C Y，AREF W G．The new casper：Query processing for location services without compromising privacy［C］／／Proceedings of the International Conference on Very Large Data Bases（VLDB’06）．Seoul，Korea，2006：763－774．

［4］GEDIK B，LIU L．Location privacy in mobile systems：A personalized anonymization model［C］／／Proceedings of the IEEE International Conference on Distributed Computing Systems（ICDCS’05）．Ohio，USA，2005：620－629．

［5］朱怀杰，王佳英，王斌，等．障碍空间中保持位置隐私的最近邻查询方法［J］．计算机研究与发展．2014，51（1）：115－125．

［6］FIROOZJAEI M D，YU J，KIM H．Privacy preserving nearest neighbor search based on topologies in cellular networks［C］／／Proceedings of the IEEE International Conference on Advanced Information Networking and Applications Workshops．Suwon，Korea，2015：146－149．

［7］INDYK P，WOODRUFF D，Polylogarithmic private approximations and efficient matching［C］／／Proceedings of the Third Theory of Cryptography Conference（TCC’06），New York，USA，2006：245－264．

［8］KHOSHGOZARAN A，SHAHABI C．Blind evaluation of nearest neighbor queries using space transformation to preserve location privacy［C］／／Proceedings of the International Symposium on Spatial and Temporal Databases（SSTD’07），Massachusetts，USA，2007：239－257．

［9］YIU M L，JENSEN C S，HUANG X，et al．Spacetwist：Managing the trade－offs among location privacy，query performance，and query accuracy in mobile services［C］／／Proceedings of the IEEE International Conference on Data Engineering（ICDE’08）．Cancun，Mexico，2008：366－375．

［10］NI W W，ZHENG J W，CHONG Z H．HilAnchor：Location privacy protection in the presence of users’preferences［J］．Journal of Computer Science and Technology，2012，27（2）：413－427．

［11］GONG Z，SUN G，XIE X．Protecting privacy in location－based servicesusing k－anonymity without cloaked region［C］／／Proceedings of the International Conference on Mobile Data Management（MDM’10）．Missouri，USA，2010：366－371．

［12］CHOR B，GOLDREICH O，KUSHILEVITZ E，et al．Private information retrieval［C］／／Proceedings of the Thirty－sixth Annual Symposium on Foundations of Computer Science（FOCS’95）．Wisconsin，USA，1995：41－50．

［13］KHOSHGOZARAN A，SHAHABI C，SHIRANI－MEHR H．Location privacy：Moving beyond k－anonymity，cloaking and anonymizers［J］．Knowledge and Information Systems，2011，26（3）：435－465．

［14］GHINITA G，KAINIS P，KHOSHGOZARAN A，et al．Private queries in location based services：Anonymizersare not necessary［C］／／Proceedings of the ACM Special Interest Group on Management of Data（SIGMOD’08）．British Columbia，Canada，2008：121－132．

［15］PAPADOPOULOS S，BAKIRAS S，PAPADIAS D．Nearest neighbor search with strong location Privacy［C］／／Proceedings of the International Conference on Very Large Data Bases Endowment（VLDB’10）．Singapore，2010，3（1）：619－629．

［16］王璐，孟小峰．位置大数据隐私保护研究综述［J］．软件学报，2014，25（4）：693－712．

［17］WILLIAMS P，SION R．Usable PIR［C］／／Proceedings of the Network and Distributed System Security Symposium（NDSS’08）．California，USA，2008：1－11．

［18］MOURATIDIS K，HADJIELEFTHERIOU M，PAPADIAS D．Conceptual partitioning：An efficient method for continuous nearest neighbor monitoring［C］／／Proceedings of the ACM Special Interest Group on Management of Data（SIGMOD’05）．Maryland，USA，2005：634－645．