一种高效的保护隐私的轨迹相似度计算框架

刘曙曙，刘 安，刘冠峰，李直旭，赵 雷，郑 凯

（1．苏州大学 计算机科学与技术学院，江苏 苏州 215006；2．江苏省软件新技术与产业化协同创新中心，南京 210008）

0 引 言

随着移动通信和定位技术的发展，近年来涌现出各种各样的移动定位设备，催生了一批基于轨迹数据的应用，然而这也大大提高了个人私密信息被暴露的可能性．通过对个人运动轨迹的攻击性分析，某些时候可以准确预测个人的兴趣爱好，行为模式，生活习惯等个人隐私．比如，通过对某一用户的日常轨迹进行分析，攻击者能够迅速辨别出用户的家庭住址和工作地址，从而为不法之徒提供了可乘之机．因此，轨迹隐私保护已经成为普通用户、工业界和学术界迫切关注的问题［1－2］．

在基于轨迹数据的应用中，轨迹之间的相似度是一个重要的度量指标，大量的与轨迹相关的分析和挖掘工作都需要进行轨迹相似度的计算．本文主要研究如何安全、准确、高效的计算轨迹相似度．具体来说，既要保证轨迹数据本身不被泄露，又要保证计算所得的轨迹相似度的准确性．

1 轨迹隐私保护技术

近年来，轨迹数据的隐私保护问题得到了广泛的重视［3］．在早期的研究工作中，主要通过对原始轨迹数据进行一定程度的处理，在尽量保证轨迹数据可用的前提下，实现轨迹的隐私保护．主要可以分为假轨迹法、抑制法和泛化法三类［1］．泛化法是目前主流的轨迹隐私保护技术，轨迹k－匿名［4］是泛化法的代表．在位置k－匿名［5］技术中，它通过对移动对象在某一时刻的位置进行泛化，从而保证这一时刻，该位置无法与其他k－1个用户位置相区别．这一思想应用于轨迹隐私保护技术中，产生了轨迹k－匿名，一般来说，k值越大则隐私保护效果越好，然而丢失的信息也越多．其不足之处在于，由于只适用于特定背景知识下的攻击从而存在着严重的局限性［6］．

差分隐私［7－9］完美的解决了这一问题．与传统隐私保护方法不同之处在于，差分隐私定义了一个极为严格的攻击模型，并对隐私泄露风险给出了严谨、定量化的表示和证明［10］，因此能够防止攻击者拥有任意背景知识下的攻击并提供有力的保护．差分隐私保护方法的最大优点是，虽然基于数据失真技术，但所加入的噪声量与数据集大小无关，因此对于大型数据集，仅通过添加极少量的噪声就能达到高级别的保护［10］．

尽管k－匿名和差分隐私技术能够保证在不纰漏任何用户轨迹隐私的情况下实现具有代表性的信息的发布，但是在本文中，我们需要计算的是两用户持有的轨迹数据之间的相似度，要求在计算中保证两用户的私有轨迹信息的隐私安全，故以上两种技术并不适用．

2 问题定义

在本文中，我们假设存在两个用户Alice和Bob，他们分别持有一条轨迹数据．现Alice和Bob均希望得到彼此轨迹的相似度，同时又不希望将各自的轨迹数据暴露给对方．一种最直接的解决方法就是两方将各自的轨迹数据都发送给一个可信的第三方，由第三方完成轨迹相似度的计算，并将结果反馈给他们．但是在实际生活中，完全可信赖的第三方是并不存在的．因此，如何在不泄露两参与方轨迹数据的前提下，实现两方轨迹相似度的计算是本文的关注点．

安全的轨迹相似度计算定义：Alice持有轨迹P＝［p1，p2，p3，…，p｜p｜］，Bob持有轨迹Q＝［q1，q2，q3，…，q｜q｜］，在不向对方泄露轨迹也不借助第三方的情况下，计算出两方轨迹的相似度，并且双方同时知道比较的结果．

攻击模型：我们假设Alice和Bob都是半诚实的，两方将严格的执行协议，但是计算过程中两方也会尽可能的根据中间信息推测出更多的额外信息．针对恶意攻击模型的安全协议虽然存在，但是计算代价过大，在实际中并不实用．而针对半诚实模型的安全协议不但能够实现高效的计算，而且对恶意攻击模型下的安全协议研究具有重要参考价值．

轨迹相似度［11］一般是轨迹点距离的聚合函数．目前比较常见的度量标准有Closest－Pair Distance（CPD），Sum－of－Pairs Distance（SPD），Dynamic Time Warping（DTW），Longest Common Subsequence（LCSS），Edit Distance with Real Penalty（ERP）和Edit Distance on Real Sequence（EDR）等．篇幅所限，本文仅仅使用DTW作为轨迹相似度的度量标准，但是本文提出的计算框架也很容易扩展到其他轨迹相似度的度量标准．

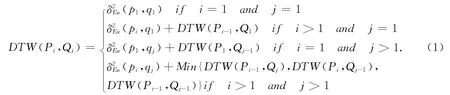
在轨迹相似度实际使用中，我们将DTW算法分为两个独立步骤完成．在步骤一中，我们需要计算出两条所有点对之间的欧氏距离的平方值（pi，qj）；在步骤二中，使用公式1中算法依次填充｜P｜×｜Q｜的矩阵M｜P｜｜Q｜．具体计算过程如下图1所示．

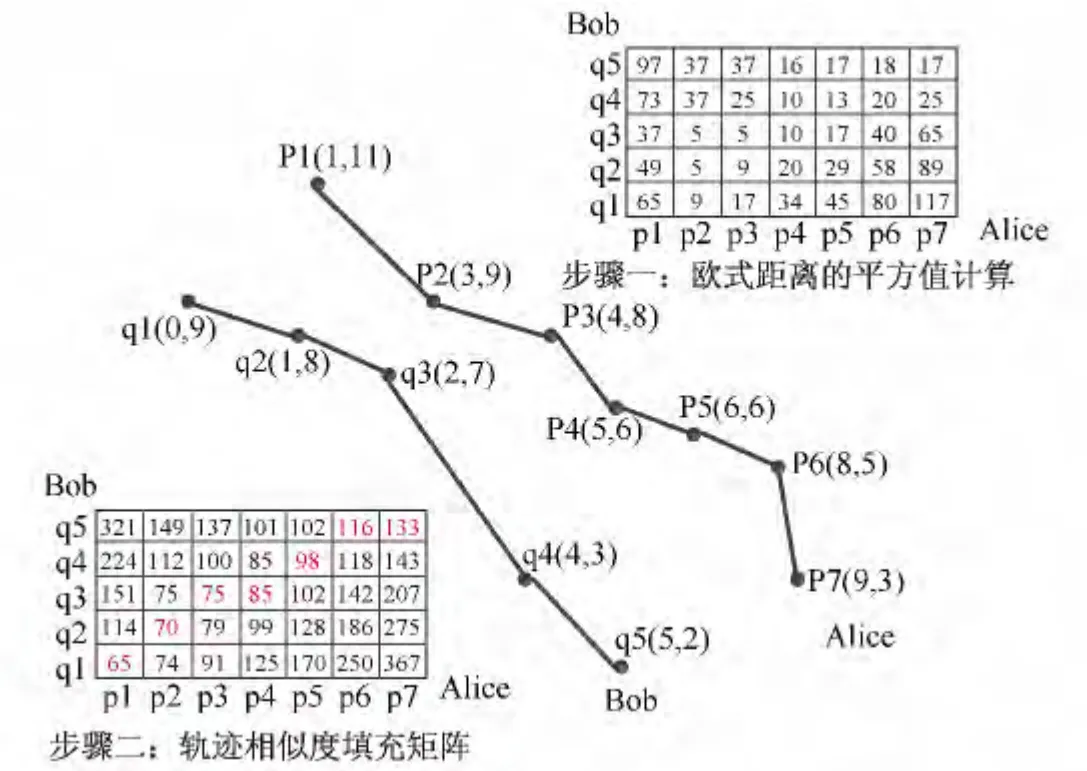
图1 基于DTW算法的轨迹相似度计算Fig．1 Computation of trajectory similarity based on DTWalgorithm

如图1所示，Alice持有轨迹P＝［p1，p2，p3，…，p7］，Bob持有轨迹Q＝［q1，q2，q3，…，q5］，为了计算Alice和Bob的轨迹相似度，在步骤一中，我们需要计算出两条轨迹所有点对之间的欧氏距离的平方值；在步骤二中，根据DTW算法用元素mi，j＝DTW（Pi，Qj）依次填充｜P｜×｜Q｜的轨迹相似度矩阵M｜P｜｜Q｜．矩阵顶角元素m｜P｜，｜Q｜＝133即为轨迹P和Q的相似度．由上可知，DTW算法的时间复杂度为O（｜P｜｜Q｜）．

3 保护隐私的轨迹相似度计算方法

3．1 基于同态加密的方法

Paillier加密系统［12］是Paillier于1999年发明的用于公钥加密的概率非对称算法．该加密系统具有加法同态性质，即两个密文乘积的解密值，与两密文对应明文的和相等，同时密文的k次幂解密值，与k和对应明文的乘积相等．Paillier加密系统的语义安全特性保证了攻击者无法由给定密文导出任何相关明文信息．

基于Paillier同态加密技术，Zhu等人提出了一个高效的保护隐私的时序数据相似度计算方法［13］．在步骤一中，利用Paillier加密系统的加法同态性质，数据持有双方可以方便基于密文计算出欧式距离的平方值［14－15］，其值以密文形式由一方持有．同时，Paillier加密系统的语义安全特性使得其能够保证攻击者无法由给定密文导出任何相关明文信息．在步骤二中，问题的关键是如何从三个值中安全有效的选出最小值．利用数据的保序特性，Zhu等人提出了一个安全的两方协议进行最小值计算，基于这个最小值计算协议和Paillier加密系统的同态性质，我们可以顺利完成轨迹相似度矩阵的填充，并保证数据信息安全无泄漏．

假设Alice的轨迹中｜P｜＝m，Bob的轨迹中｜Q｜＝n，k是最小值协议中为了达到干扰效果而添加的随机数个数．那么在这一方案中，Bob端共需4mn次加密操作，4mn次解密操作，Alice端需要mn（k＋1）次加密操作．

尽管该方法能够保证轨迹相似度计算过程中两参与方数据的隐私安全，但是为了达到足够的隐私安全，在最小值协议中为了达到干扰效果而添加的随机数个数k必须足够大，为此两端都必须对额外的k个随机数进行额外的加解密操作，由此将产生大量额外的计算和通信开销．

3．2 基于Yao协议的方法

Yao协议［16－17］允许两个半诚实参与方分别输入x和y作为一个任意函数f（x，y）的输入，能够准确计算函数值并且保证除了最终结果外，没有任何关于输入或者中间值的相关信息泄露．为了实现轨迹相似度的计算，本文需要使用到2－MUL，2－ADD，2－SUB和2－MIN四个基本电路模块［16，18］．他们都是利用Yao协议实现的Garbled Circuit基本模块，其中，2－MUL可以实现任意L位整数之间的乘法，2－ADD可以实现任意两个L位整数之间的加法，2－SUB与2－AND类似，2－MIN可以实现任意两个L位整数之间的比较，输出结果为较小值．

为了计算轨迹相似度，首先需要实现欧氏距离平方值计算单元和最小值选择单元．利用欧式距离平方值计算电路单元，我们可以实现步骤一中两轨迹所有点对之间欧式距离的平方值计算，其计算结果将以电路密文形式由Alice和Bob两参与方共享．在步骤二中，利用最小值选择单元和步骤一得到的欧氏距离平方值，可以顺利完成相似度矩阵M｜P｜｜Q｜的填充，最终，只需对矩阵顶角元素m｜P｜，｜Q｜＝DTW（P，Q）解密，即可得到轨迹P和Q的相似度明文结果．

电路基本单元模块设计如图2所示，其中左边为欧式距离平方值计算模块，中间对应相似度矩阵更新过程中边界值更新，右边对应除边界值外的其他单元格更新方法．基于这三个电路模块，即可顺利实现安全的轨迹相似度计算．

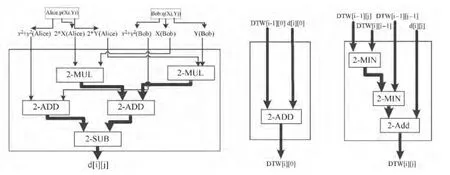
图2 基于Yao协议的轨迹相似度计算的电路模块设计Fig．2 Circuit module design of trajectory similary computation based on Yao’s protocol

在上面的电路模块中，箭头代表数据的流向，细线表示数据输入为明文，粗线表示数据输入为电路密文，电路密文使用两参与方密钥双重加密而成，从而保证在两参与方不勾结的情况下，任一方都无法获取相关信息．在整个计算过程中，仅对最终结果m｜P｜，｜Q｜＝DTW（P，Q）解密，从而保证了计算过程中所有中间数据的安全性．

因为异或操作在电路实现中是免费的［19］，所以在电路复杂度计算中，仅需讨论除异或操作外的其他操作．Kolesnikov［18］指出，一个L－bit的加法单元可以通过L个1位的全加器实现，而实现1个1位的全加器需要借助1次与操作，故一个L－bit的加法器共需L次与操作．同理，可以统计得到一个L－bit的乘法单元共需与操作2L2－2L次；一个L－bit的最小值选择单元共需与操作L次；一个L－bit的减法单元共需与操作L次．

当Alice的轨迹中｜P｜＝m，Bob的轨迹中｜Q｜＝n，轨迹中经纬度分别用L－bit的整数表示，分析可知，在DTW迭代计算过程中，共需调用欧式距离平方值计算模块m＊n次，调用边界更新模块m＋n－2次，调用内部更新电路模块（m－1）（n－1）次．因此，轨迹相似度计算电路共需实现与操作16L2（2mn－m－n＋1）＋2L（mn＋2m＋2n－3）次．

3．3 结合同态加密和Yao协议的方法

通过观察可以发现，在欧式距离平方值计算过程中，利用Yao协议实现的电路版本因为大量乘法和加法电路的使用使得其计算复杂度相对较高，由此带来了大量的计算开销和内存消耗，相比之下，Paillier同态加密方法显得更为实用．同样，在矩阵相似度更新操作中，利用Paillier同态加密方法实现的最小选择协议需要对大量随机数进行加解密操作，因而在性能上远不如Yao协议．于是提出了第三种方法，针对轨迹相似度计算过程中的不同步骤具有不同的计算特点，交替使用同态加密系统和Yao协议，从而高效地完成轨迹相似度计算．在这个方法中，两轨迹所有点对之间的欧氏距离平方值运算通过Paiiler同态加密方案实现，出于对中间数据的安全考虑和下一步中对Yao协议的输入要求，我们要求最终结果必须以和的形式由两参与方共享，现对算法进行如下修改．

Alice：

（2）产生一系列随机值R＝｛r1，r2，r3，…，r｜P｜＊｜Q｜｝，

Bob：

在步骤二中，我们对电路模块做出如下调整，如图3所示，左边模块用于相似度矩阵中的边界值更新，右边用于除边界值外的其他单元格．

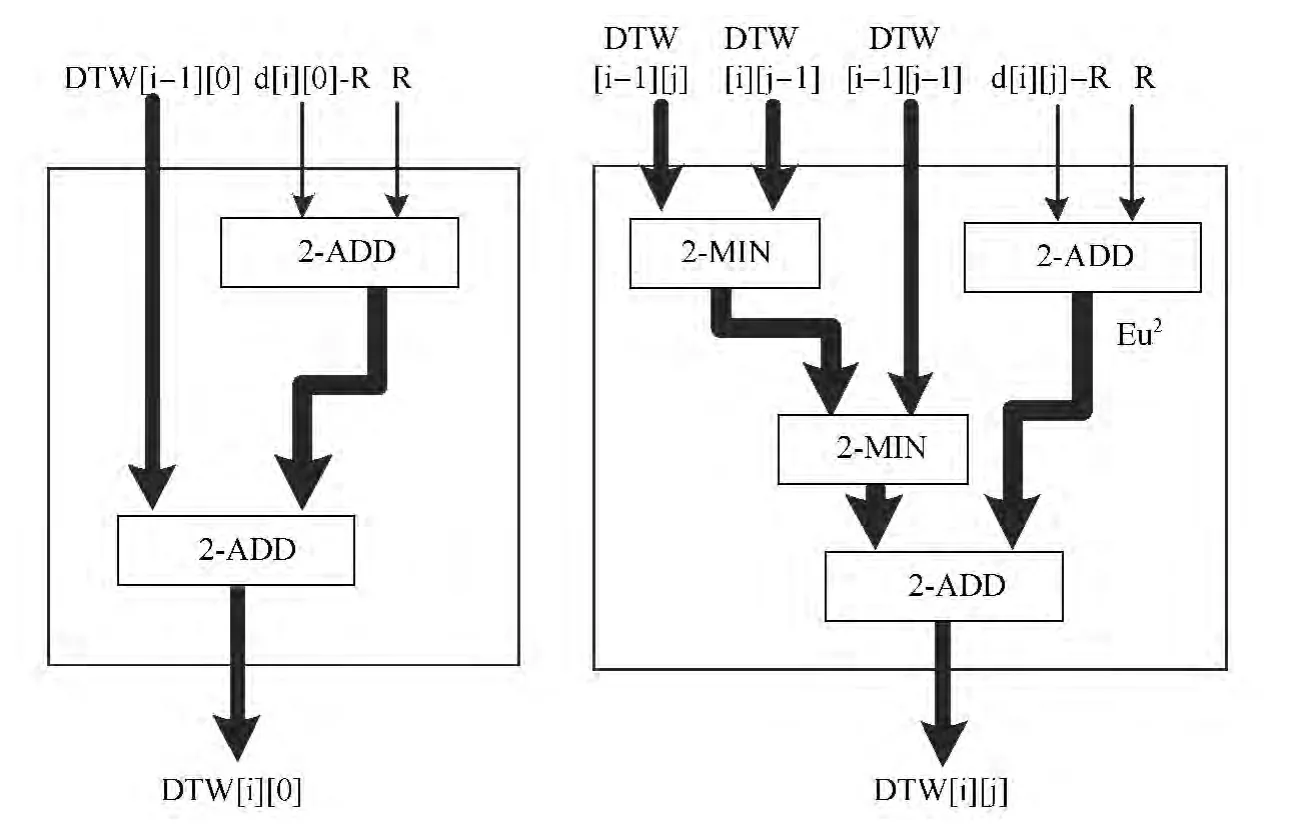
图3 相似度矩阵更新模块Fig．3 Updating module of similarity matrix

因为欧式距离平方值计算和相似度矩阵更新是两个独立的部分，所以在复杂度分析时两个部分单独考虑．在欧式距离平方值计算部分，Alice需要3m＋mn次加密操作，Bob需要m次加密和mn次解密操作．在电路部分，共需实现与操作2L（4mn－2m－2n＋1）次．

4 实验结果及分析

对于以上提出的三种算法（为了方便讨论，三种算法依次命名为DTW－Paillier，DTWYao和DTW－Hybrid），我们通过实验进行了性能比较．实验用服务器的具体配置是：2．53 GHz CPU，256GB RAM，centos 7和JDK7．实验中，Alice和Bob之间的通信通过Socket实现，实验中不存在任何共享信息或可信第三方．

实验中，轨迹点的数据位数L一般设置为15位．为了保证加密数据的安全性，实验中统一使用1024位的Paillier加密系统进行加解密操作，其安全性相当于80位对称密钥，使用此加密方法加密后的数据披露风险为1／280，在现实应用中完全可以忽略不计．

为了测试轨迹长度对算法性能的影响，轨迹长度以步长为10从10增长到100．为了作图方便，我们假设Alice和Bob持有的轨迹的具有相同的长度．

图4比较了三种算法的运行总时间．左图为各算法在Alice端的运行时间统计，右图为各算法在Bob端的运行时间统计．从图中可以看到DTW－Paillier耗时最长，DTW－Yao其次，而本文提出的DTW－Hybrid效率最高．从第三节的复杂度分析中可以看出，尽管算法的运行时间都与轨迹长度的平方成正比，但是得益于时间基数及比例系数优势，随着轨迹长度不断的增加，DTW－Hybrid算法的优势越来越突出，在轨迹长度为100时，效率提高近200倍．

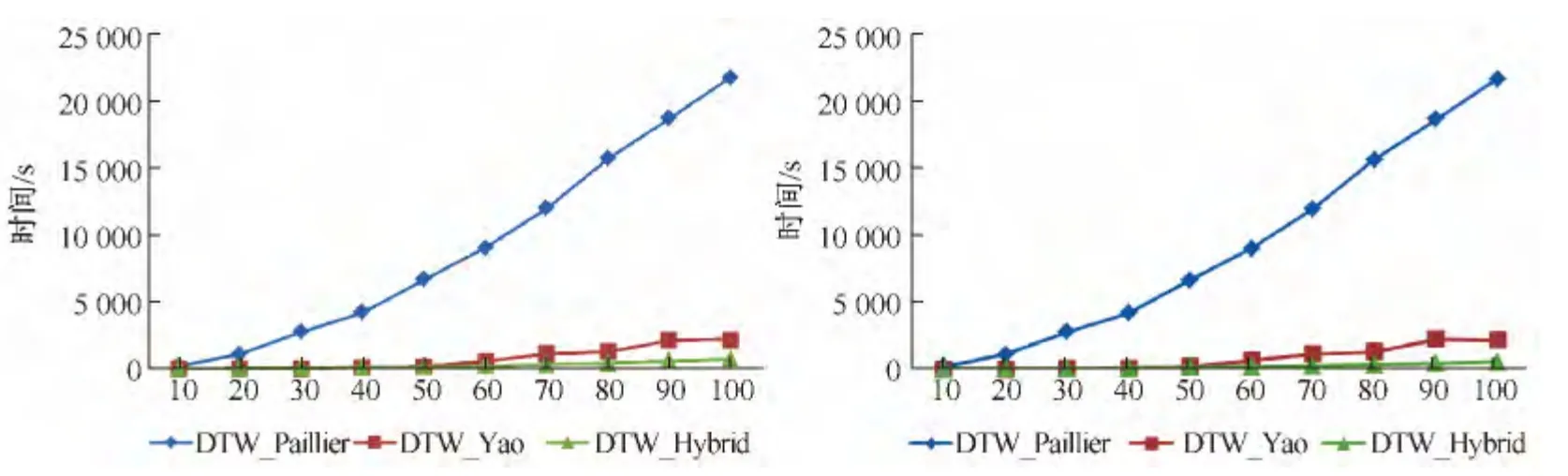
图4 DTW＿Paillier，DTW＿Yao和DTW＿Hybrid的性能比较Fig．4 Performance comparison about DTW＿Paillier，DTW＿Yao，and DTW＿Hybrid

如前所述，DTW＿Hybrid包含两个阶段：基于Paillier同态加密系统的欧氏距离平方值计算和基于Yao协议的相似度矩阵更新．我们分别对这两个阶段的时间进行了统计．左图为Alice端时间统计，右图为Bob端时间统计，从图5可以看到，两个阶段的时间与之前给出的计算复杂度理论分析基本一致．

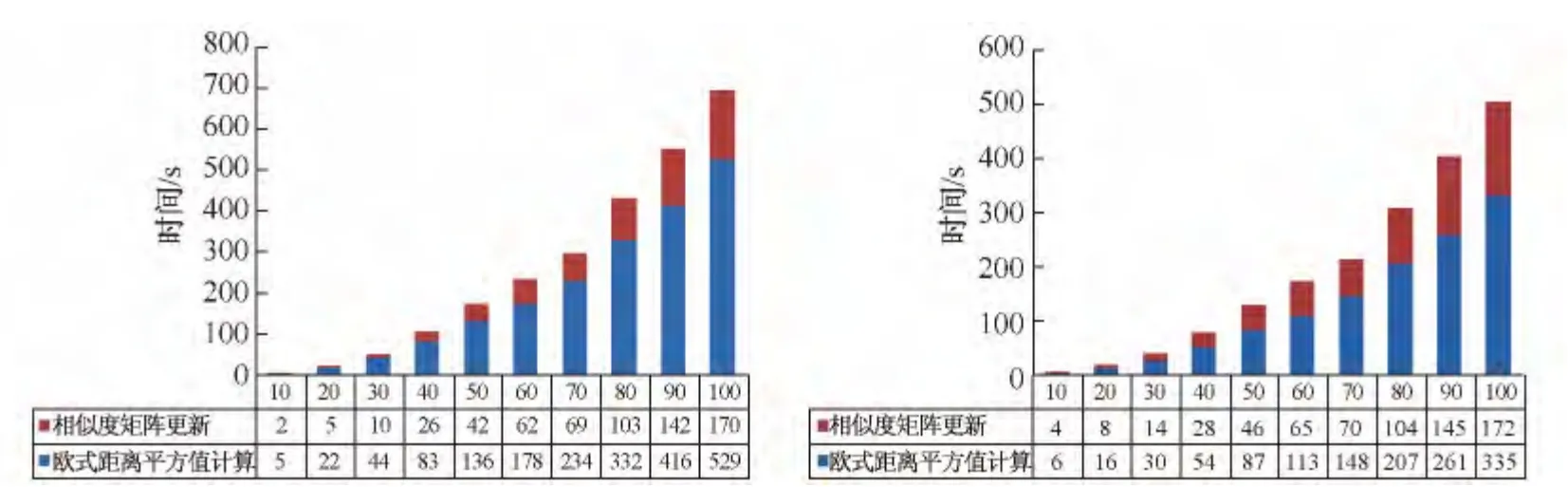
图5 欧式距离平方值计算和相似度矩阵更新的性能比较Fig．5 Performance comparison about computation of Euclidean distance squared and updating of similarity matrix

从图5可以发现，在DTW＿Hybrid中，欧式距离平方值计算耗时相对较长，在整个方法中占据了75%左右．因此，对欧式距离平方值计算进行进一步优化将有助于大幅度缩短算法的整体运行时间．在实验中，利用并行技术对欧式距离平方值的计算进行了进一步优化，优化后的DTW＿Hybrid的性能如图6所示．同样，左图为Alice端时间统计，右图为Bob端时间统计．可以看到，在使用6个线程时，Alice的计算时间大约减少到原来的19%，而Bob的计算时间大约减少到原来的24%．

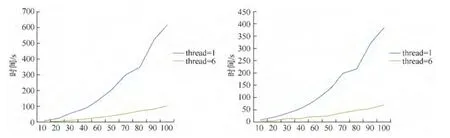
图6 单线程和多线程的性能比较Fig．6 Performance comparison about single thread and muti thread

5 结论与展望

本文提出了一个保护隐私的轨迹相似度计算框架．该框架能够确保持有轨迹的两方不能得到除了轨迹相似度以外的其他任何信息，从而同时保护了两方的轨迹数据隐私．该框架针对轨迹相似度的计算特点，通过结合同态加密和Yao协议，显著提高了计算性能．实验结果表明本框架明显优于已有的保护隐私的轨迹相似度计算方法．通过分析目前常见的轨迹相似度度量标准，可知轨迹相似度计算主要涉及到欧式距离计算，最小值选择或者最大值选择等操作，这在本文提出的计算框架中均可得到高效地实现．下一步将在真实的轨迹数据上进一步优化本文提出的计算框架．

［1］霍峥，孟小峰．轨迹隐私保护技术研究［J］．计算机学报，2011，34（10）：1820－1830．

［2］霍峥，孟小峰，黄毅．PrivateCheckIn：一种移动社交网络中的轨迹隐私保护方法［J］．计算机学报，2013，36（4）：716－726．

［3］CHEN L，ÖZSU M T，ORIA V．Robust and fast similarity search for moving object trajectories［C］／／Proceedings of the 2005 ACM SIGMOD international conference on Management of data．ACM，2005：491－502．

［4］ABUL O，BONCHI F，NANNI M．Never walk alone：Uncertainty for anonymity in moving objects databases［C］／／Data Engineering，2008．ICDE2008．IEEE24th International Conference on．Ieee，2008：376－385．

［5］GRUTESER M，GRUNWALD D．Anonymous usage of location－based services through spatial and temporal cloaking［C］／／Proceedings of the 1st international conference on Mobile systems，applications and services．ACM，2003：31－42．

［6］LI N，LI T，VENKATASUBRAMANIAN S．t－closeness：Privacy beyond k－anonymity and l－diversity［C］／／Data Engineering，2007．ICDE2007．IEEE23rd International Conference on．IEEE，2007：106－115．

［7］DWORK C．Differential privacy［M］／／Encyclopedia of Cryptography and Security．US：Springer，2011：338－340．

［8］DWORK C．Differential privacy：A survey of results［M］／／Theory and Applications of Models of Computation．Berlin Heidelberg：Springer，2008：1－19．

［9］DWORK C，LEI J．Differential privacy and robust statistics［C］／／Proceedings of the forty－first annual ACM symposium on Theory of computing．ACM，2009：371－380．

［10］张啸剑，孟小峰．面向数据发布和分析的差分隐私保护［J］．计算机学报，2014（4）：018．

［11］DENG K，XIE K，ZHENG K，et al．Trajectory indexing and retrieval［M］／／Computing with spatial trajectories．New York：Springer，2011：35－60．

［12］PAILLIER P．PUBLIC－key cryptosystems based on composite degree residuosity classes［C］／／Advances in cryptology－EUROCRYPT＇99．Berlin Heidelberg：Springer，1999：223－238．

［13］ZHU H，MENG X，KOLLIOS G．Privacy Preserving Similarity Evaluation of Time Series Data［C］／／EDBT，2014：499－510．

［14］INAN A，KANTARCIOGLU M，BERTINO E，et al．A hybrid approach to private record linkage［C］／／Data Engineering，2008．ICDE2008．IEEE24th International Conference on．IEEE，2008：496－505．

［15］HU H，XU J，REN C，et al．Processing private queries over untrusted data cloud through privacy homomorphism［C］／／Data Engineering（ICDE），2011 IEEE27th International Conference on．IEEE，2011：601－612．

［16］YAO A C C．How to generate and exchange secrets［C］／／Foundations of Computer Science，1986．27th Annual Symposium on．IEEE，1986：162－167．

［17］LINDELL Y，PINKAS B．A proof of security of Yao＇s protocol for two－party computation［J］．Journal of Cryptology，2009，22（2）：161－188．

［18］KOLESNIKOV V，SADEGHI A R，SCHNEIDER T．Improved garbled circuit building blocks and applications to auctions and computing minima［M］／／Cryptology and Network Security．Springer Berlin Heidelberg，2009：1－20．

［19］KOLESNIKOV V，SCHNEIDER T．Improved garbled circuit：Free XOR gates and applications［M］／／Automata，Languages and Programming．Berlin Heidelberg：Springer，2008：486－498．