轨迹数据压缩综述

江俊文，王晓玲

（1．上海市高可信计算重点实验室，上海 200062；2．华东师范大学 数据科学与工程研究院，上海 200062）

0 引 言

近年来，随着移动设备的普及和定位服务的发展，在这些应用中产生了大量的轨迹数据．例如，车载GPS设备记录车辆每时每刻的位置；在微博、街旁、Fousquare等移动社交网络上，用户的签到序列可以看作是该用户的旅游轨迹；公交卡、地铁卡的刷卡记录显示了人们何时何地上车或下车，组成了人们的出行轨迹．

基于位置服务需要处理大量的轨迹数据，比如路线规划、时间预测等．但是海量轨迹数据为基于位置服务带来了许多新的挑战，如：①数据规模快速增长，导致数据存储面临巨大压力；②基于海量轨迹数据的查询和数据分析性能降低；③数据的收集和传输会带来误差和冗余，从而影响服务器的响应速度．

为了解决以上问题，人们提出了许多轨迹压缩方法．输入一条轨迹，轨迹压缩方法可以输出一条占用更少空间的压缩轨迹，而压缩轨迹与原始轨迹之间的误差必须是在可接受的范围内．本文的工作有3方面：

（1）对已有轨迹压缩技术进行综述，并比较各类技术的优势和不足．

（2）介绍轨迹查询种类，并比较各类压缩后的轨迹对查询的支持情况．

（3）回顾最近几年的压缩轨迹管理系统．

轨迹数据压缩从几十年前开始就有研究．最初的轨迹压缩方法［1］只是考虑到点的空间位置，通过删除点来减小数据量．考虑到轨迹具有时间属性，文献［2－3］同时考虑时间和空间信息，在压缩轨迹的同时，满足轨迹的精度要求．随着城市路网的成熟，文献［4－10］借助路网结构，把轨迹从点的序列转化为路段的序列，许多个轨迹点只需用一条边来表示，从而达到压缩目的．为了方便人们理解轨迹的状态，使用兴趣点（Point of Interest，POI）来记录轨迹经过的重要位置是一种很好的方法［11－12］，对于城市中熟悉的POI，人们能比较容易看懂轨迹的运行踪迹．

空间对象可分为点、区域和轨迹3类．针对点、区域和轨迹之间的空间位置关系，轨迹查询处理返回满足条件的对象．为了加快筛选的速度，通常需要设计索引结构．另外，轨迹查询可以结合文本数据．把点、区域和轨迹加入文本描述，转变为关键字查询．关键字查询的种类很多，本文在第2节中将主要介绍最常见的3种关键字查询类型．

轨迹管理系统的功能包括组织数据、建立索引、提供应用接口．为了更好地管理数据，系统会对数据进行压缩，而对压缩数据建立合适的索引可以加快上层查询的速度．因此轨迹管理系统是结合轨迹压缩和轨迹查询的综合性系统．

本文以下的部分组织如下：第1节回顾3类轨迹压缩技术和各类中已有重要的轨迹压缩方法算法；第2节介绍基于压缩轨迹的查询处理；第3节介绍已有的轨迹管理系统，包括集中式的轨迹数据库和分布式轨迹数据库；第4节对已有工作进行总结和比较，并展望未来的工作方向．

1 轨迹压缩方法

轨迹压缩方法从技术上主要分为3类，如图1所示．第一类是不基于路网结构的数据压缩，也叫线段简化压缩（Line Simplification）方法，目标是在误差允许范围内减少轨迹点的数目，其又可分为线下压缩（又称为离线压缩）（Batched Model Based Compression，简称Batched Compression）和在线压缩（Online Compression）．第二类是基于路网结构的压缩（Map－Matching Based Compression），它需要把轨迹点映射到路段上，结合路网结构来表示原始轨迹，从而减小数据量．第三类是语义压缩（Semantic Compression），即是把原始轨迹转换为POI序列来表示，这样有利于人们理解轨迹的含义．

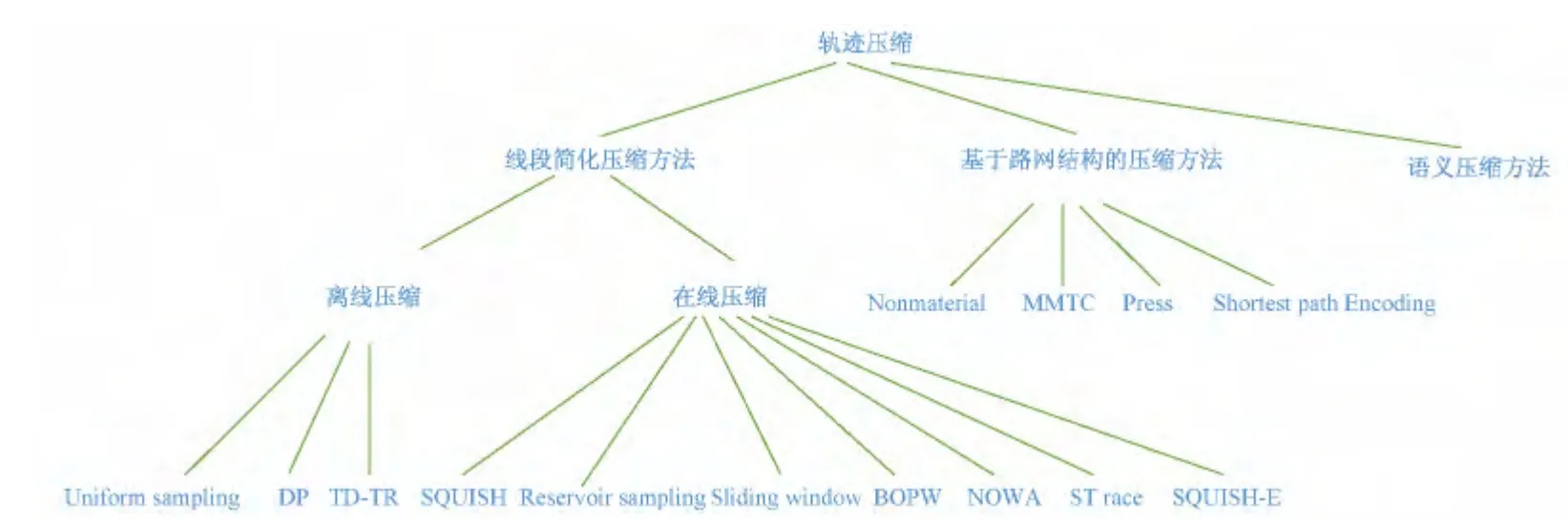
图1 轨迹压缩方法分类Fig．1 Trajectory compression methods category

1．1 线段简化压缩方法

轨迹是指移动物体在空间中的位置随着时间变化的函数．物体的移动踪迹是连续的，而我们通过GPS设备能采样到是一些离散的点，每个点由三元组〈x，y，t〉表示，x和y是点的经纬度，t表示时间戳．因此一条轨迹T可以近似用一些点的序列表示：T＝｛〈x1，y1，t1〉，〈x2，y2，t2〉，〈x3，y3，t3〉，…，〈xn，yn，tn〉｝．

GPS设备的采样频率对轨迹的影响很大：若采样频率很高，轨迹就比较精确；若采样频率很低，轨迹由很少的点构成，此时轨迹与物体真实移动的路径相差很大．但是如果采样频率很高，产生更多的轨迹点，会给数据存储带来巨大的挑战．因此，我们需要在轨迹的准确率和存储空间上做权衡．线段简化压缩技术就是通过删除误差较小的点，从而优化存储，并保障轨迹的准确率从而满足需求．线段简化压缩技术［1］在1970年代就出现了，并且在图像处理、制图学上应用广泛，其主要思想是，输入一条由点组成的曲线，可以使用另外一条包含更少的点的曲线来近似原始曲线，并保证与原始曲线之间的差距较小．

把线段简化的思想运用在轨迹数据中，即是找到含有更少的点的近似轨迹来代替原始轨迹，从而达到压缩轨迹的目的．与单纯的曲线不同的是，轨迹数据不仅仅只有位置信息，还有时间、速度、方向信息．如何改进线段简化方法，使之更适合轨迹，也是一直以来研究的方向．线段简化压缩技术可分为两类：第一类是叫做离线压缩技术（Batched Compression Technique），它先收集完一整条轨迹采样点，然后删除数据中冗余的点．由于这种方法是考虑了整条完整的轨迹，因此比其他方法更容易做到全局更优，但是需要消耗更多的时间，适合线下处理、分析数据的场景．第二类是在线压缩技术（Online Compression Technique），适合需要及时更新移动物体的位置或者实时交通状况的场景．

1．1．1 离线压缩技术

离线压缩方法中最简单的一种就是均匀采样（Uniform Sampling）算法．算法的主要思想是每隔K个点保留1个点，比如第1，5，9个点，中间的点都删除．产生的新的轨迹大致上是原始轨迹的骨架．均匀采样算法的效率极高，计算代价很小，缺点是不能保留轨迹的细节．比如一些转弯的点会被跳过，从而导致近似轨迹和原始轨迹之间的误差很大．

轨迹压缩算法应该保留更合适的轨迹点，而不是随机地保留轨迹点．Douglas－Peucker算法（DP）［1，13］是一种可以保留重要点的压缩算法，主要思想是用若干个线段来代替原始轨迹．首先，把轨迹上第一个点和最后一个点之间的直线线段作为近似轨迹，对中间的点计算点到线段的垂直欧氏距离（Perpendicular Euclidean Distance），选出具有最大的距离的点，如果最大距离超过预先设定的距离阈值，那么把这个点作为分裂点加入到近似轨迹中，并把整条轨迹分为两段子轨迹．对两段子轨迹分别重复上述步骤，直到子轨迹里面的最大垂直欧氏距离小于距离阈值或者轨迹内只有2个点（起点和终点）．DP算法以从上到下的方式分解轨迹，得到近似轨迹．误差的衡量是用垂直欧氏距离度量．通过下面的例1来具体阐述算法的步骤．

例1 有1条轨迹T，如图2（a）所示．T中包含｛p0，p1，p2，p3，p4，p5，p6，p7，p8｝9个轨迹点．根据DP算法，第一步，轨迹的起点和终点的连线线段作为近似轨迹，计算其余各点到的垂直欧氏距离．其中一些垂直欧氏距离或许会大于预先设定的阈值，那我们找到最大的垂直欧氏距离，比如图2（a）中是p2点，则p2点被选为分裂点．因此在算法的第二步，p0，p2，p8组成了近似轨迹，如图2（b）所示.和两条线段作为近似轨迹，此时计算其他轨迹点到对应线段的垂直欧氏距离．在部分，没有轨迹点的垂直欧氏距离大于阈值，因此可以作为近似轨迹的一部分．在部分，由于轨迹点p5的垂直欧氏距离大于阈值，且最大，那么p5作为分裂点，继续进行分裂，直到所有的轨迹点到对应近似线段的垂直欧氏距离不再大于阈值．

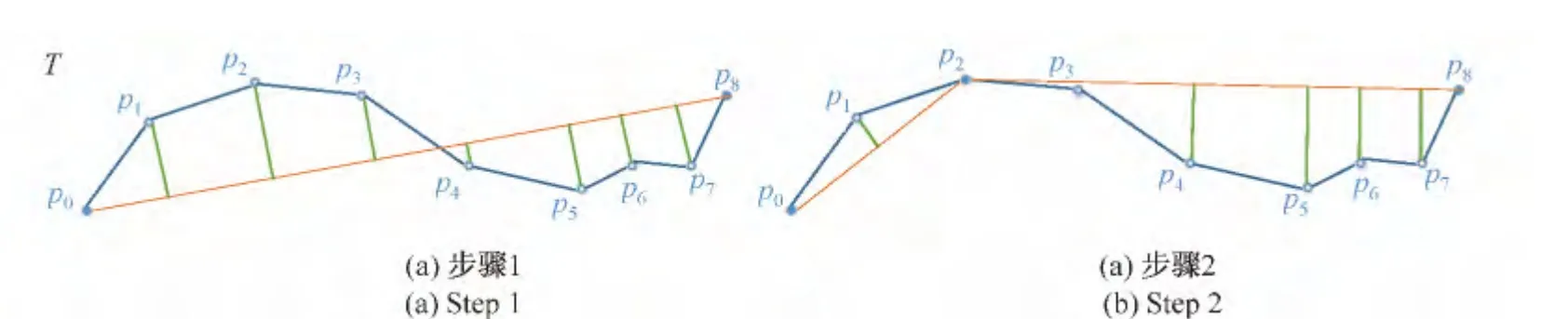
图2 DP算法Fig．2 DP algorithm

DP算法的思想简单且性能较好，在各个领域都有广泛的应用．文献［8］对比了DP算法与其他算法的性能，最终在多个数据集上，DP算法在时间效率、压缩率和精度上都具有较优性能．但是DP算法的缺陷是时间复杂度较高，达到O（N2），N是轨迹点的数目．文献［13］对DP算法进行了改进，借助外部存储结构，把平均的时间复杂度提高到O（N×log N）．另外DP算法的误差是用垂直欧氏距离来度量，垂直欧氏距离只考虑了位置信息，对时间信息没有考虑．而轨迹数据中的时间信息是非常重要的，因为每个轨迹点〈x，y，t〉表示的是移动物体在t时刻落在〈x，y〉位置，因此距离函数应该考虑时间信息．鉴于此，文献［14］提出了新的距离函数：时间比例的空间距离（Time－Distance Ratio Metric），根据时间比例找到近似线段上与原始轨迹点对应的位置，然后计算轨迹点和近似点之间的欧氏距离（包括垂直欧氏距离和时间同步欧氏距离等等）．文章提出了Top－Down Time－Ratio（TD－TR）算法，与DP算法的思想类似，但是使用了时间比例的空间距离作为距离函数，从而获取到更精确的近似轨迹．因为新的误差度量不仅更精确，而且还考虑了空间和时间维度．文献［15］在利用DP算法压缩时，利用凸包等数据结构，优化算法的时间复杂度和空间复杂度，最终在时间复杂度为O（n）和空间复杂度为O（1）的条件下，找到最优的压缩轨迹．

1．1．2 在线压缩技术

离线压缩方法是需要收集到完整的轨迹之后进行压缩，所以能获得全局较优的近似轨迹．然而，这种离线压缩方法并不能适用于所有场景．如果应用需要实时的数据，那就需要在线压缩技术．

蓄水池算法（Reservoir Sampling）能实时等概率地选择轨迹点，其基本思想是维护一个大小为R的蓄水池，原始轨迹T的轨迹点一个一个过来时，若蓄水池没有满，那么把轨迹点放入蓄水池．若蓄水池满了，则先判断新来的轨迹点是否要放入蓄水池：若判断为负，则该轨迹点舍弃掉；若判断为正，则从蓄水池中的轨迹点中随机选择一个并舍弃，然后把新的轨迹点放入．每个轨迹点最终留在蓄水池内的概率是相等的，概率值为R／N，N是原始轨迹长度．蓄水池算法的时间复杂度为O（R×（1＋log N／R））．

蓄水池算法的效率很大，但没有考虑轨迹点的时间顺序、空间顺序和重要性．因此蓄水池算法会产生很大的误差．鉴于此，文献［2］提出了Sliding Window和Open Window两种算法，能更好地选取轨迹点．

Sliding Window的主要思想是从轨迹起点开始，初始化一个大小为1的滑动窗口，并逐步增大窗口的大小，从而逐步加入后续的轨迹点．把窗口内的第一个轨迹点和最后一个轨迹点进行连接，得到的线段作为近似线段．然后计算近似线段与原始轨迹的垂直欧氏距离，若距离小于预先设定的距离阈值，则继续增大滑动窗口的大小，直到窗口内的误差小于设定的距离阈值．

例2 如图3（a）所示，表示了Sliding Window算法的基本思想．以p0为起点，初始化滑动窗口为｛p0，p1｝．当新的p2轨迹点加入滑动窗口内，以线段作为p0，p1，p2部分的近似轨迹，计算p1点和线段之间的垂直欧氏距离．若距离小于阈值，那么继续扩大窗口大小，加入新的轨迹点p3，滑动窗口包含｛p0，p1，p2，p3｝，以线段为近似轨迹，计算窗口内其他点的垂直欧氏距离．由于距离已经超过设定的距离阈值，所以之前的窗口状态｛p0，p1，p2｝被选作近似轨迹的一段．接着以p2为新的滑动窗口的起点，加入p3，p4，重复之前的步骤，直到轨迹的终点．图3（a）中原始轨迹最终被简化为｛p0，p2，p5，p8｝．

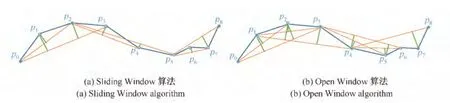
图3 算法Fig．3 Algorithm

Open Window与Sliding Window类似，设定一个窗口，在窗口内进行数据压缩．与Sliding Window不同的是，Open Window计算窗口内每个点的垂直欧氏距离和时间同步欧氏距离，可以选取窗口内误差总和大于阈值时，窗口内的倒数第二个轨迹点作为该窗口的近似线段的终点（Before Open Window，BOPW），也可以选取窗口内贡献最大距离的轨迹点作为该窗口的近似线段的终点（Normal Open Window，NOPW）．以图3（b）为例，如果使用NOPW进行压缩，得到的压缩后的轨迹为｛p0，p1，p3，p4，p7，p8｝．

值得一提的是，窗口算法的每一次迭代的终止条件有很多种，比如窗口内点的数目、窗口内误差总和、窗口内误差的最大值．只要不满足任何一个条件的阈值，就可以终止当前迭代，并进入下一次迭代．

Sliding Window和Open Window只考虑当前窗口内的轨迹点的位置，因此在每个局部能做到最优，但不能兼顾全局的走势．

根据之前的运动状态可以预测下一个轨迹点的位置，如果预测准确，则下一个轨迹点可以删除；如果预测不准确，则下一个轨迹点应该保留．依据这个思想，文献［3］借助速度和方向来构造安全区域，进行筛选轨迹点，从而提出了Threshold－Guided Sampling算法，即预先设定速度和方向改变的阈值，通过最近的2个轨迹点的速度和方向，结合阈值来构造安全区域（如图4所示的扇形区域），以此来判断新到的点是否应该保存．如果新到的一个轨迹点落在安全区域内部，则该轨迹点被认为是冗余的，可以删去；如果新到的点落在安全区域外面，说明移动物体的状态发生了改变，那么这个轨迹点应该被保留下来．

例3 如图4所示，构建安全区域的例子．原始轨迹T包含｛p0，p1，p2，p3，p4，p5，p6，p7，p8｝9个轨迹点．假设p0，p1属于近似轨迹．以p1的瞬时速度和方向，结合速度和方向的误差阈值，以及p1，p2之间的时间间隔，得到安全区域（黄色区域）．由于p2落在安全区域外面，p2则保存在近似轨迹中．同理在p2处画出对应的安全区域，检测到p3落在安全区域内，那么p3被省略．重复这样的过程，直到轨迹结束．最终近似轨迹为｛p0，p1，p2，p4，p5，p8｝．

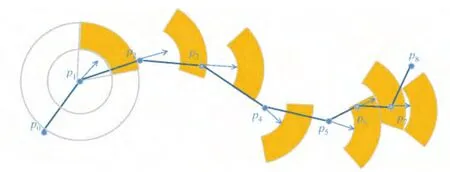
图4 Threshold－Guided Sampling算法Fig．4 Threshold－Guided Sampling algorithm

用前一个轨迹点的速度和方向构建安全区域的缺点是有误差累积效应，若一个轨迹以一个弧度慢慢变化，那么每个点都落在前一个轨迹点构造的安全区域内，结果每个点都被省略，与事实不符．因此文献［3］提出了第二种构建安全区域方法：用近似轨迹中最近的2个采样点的速度和方向作为基准，结合阈值构建安全区域．这种方法可以降低误差累计效应，但也导致了另外一个问题，那就是重要的转折点不能被发现了．因此，文献［3］最终用两种安全区域的交集作为最终的安全区域，新到的点落在这个安全区域内才被删除．此外，文献［3］还提出了STTrace算法，保证在有限的内存消耗前提下，完成对很长轨迹的压缩．其主要思想是在用来存放近似轨迹的内存溢出时，选择一个近似轨迹中的点抛弃，腾出空间给新到的近似轨迹点，但是要保证新到的轨迹点相比被抛弃的轨迹点有更好的近似效果．

文献［16］提出了SQUISH（Spatial QualIty Simplification Heuristic）在线压缩算法．与Sliding Window算法类似，SQUISH初始化了一个大小为k的优先级队列，把轨迹点加入到队列中，当队列满时，删除引起最小误差的点，并重新计算每个点的优先级．SQUISH算法的时间复杂度很低，并且压缩率较高，轨迹误差较小．但是压缩轨迹的误差并没有上界，因此，在文献［17］中提出的SQUISH－E算法是对SQUSIH的优化，它能在给定的误差阈值内达到最优的压缩率．SUQISH－E算法的最差时间复杂度为其中α是期望达到的压缩率，N是指轨迹中点的数目．

离线压缩技术和在线压缩技术的对比如下．

共同点：都是使用线段来近似原始轨迹，从而减少中间点的数目；都是在欧氏空间内进行压缩，误差使用欧氏距离测量．

不同点：离线压缩技术考虑了整条轨迹，获得全局较优的压缩轨迹；而在线压缩只考虑局部轨迹，因此相对来讲误差更大．离线压缩技术的平均时间复杂度一般比在线压缩技术的平均时间复杂度要高．

1．2 基于路网结构的压缩方法

线段简化压缩方法是基于欧氏空间的，而车辆的运动要受到路网结构的约束，因此线段简化压缩方法在车辆轨迹压缩上有很大的局限性．例如，计算出租车轨迹的行驶长度，在欧氏空间里，只需要对每段线段的长度进行求和．但是出租车在实际行驶时，并不会沿着两点之间的线段直线行驶，因为线段可能穿过湖泊或者草地．因此，不能简单地用两点之间的线段距离来当作实际的行驶距离．最近几年，城市的路网结构数据逐渐成熟，结合路网结构的轨迹压缩变得越来越流行．

为了降低轨迹数据的误差率，我们首先对原始轨迹进行Map－Matching预处理［18－19］．在原始轨迹数据中加入路网结构的好处是：首先，结合路网结构，能保证轨迹落在路段上，这更具有现实意义．其次，路网结构是稳定的，更改的频率很低，而轨迹数据却是每时每刻都在产生的．因此，路网结构的稳定性和有限性使得我们可以使用路网数据来表示轨迹数据．结合路网结构的压缩方法，通常会将轨迹点的序列转化成所经过的路段的序列，而一个城市的路段是有限的，因此我们可以把无限的轨迹点转化为有限的路段来进行表示．

文献［20］提出了Nonmaterialized算法来构造最优的压缩轨迹．首先把GPS采样点映射到路网上，得到的轨迹称为Road－Snapped Trajectory；然后通过Nonmaterialized算法把Road－Snapped Trajectory转化为路口的序列，从而压缩轨迹．

文献［4］假设司机会选择两条边之间的最短路径（Shortest Path）或者是选择转角小的边行驶，提出了最短路径算法和链接算法．最短路径算法的思想是，如果司机在两条路段之间行驶的轨迹与这两条路段之间的最短路径一致，那么直接用头尾两条路段来表示整段轨迹．链接算法的思想是，如果司机在两条路段之间行驶的轨迹每次都是沿着最小转角的路段行驶，那么只用头尾两条路段来代替整段轨迹．在执行算法之前，必须要将城市的路网结构抽象成有向图，图中的每条边即是实际路段，实际的轨迹用边的序列表示．两条路段之间的最短路径可以在图中用Dijkstra算法或者A－star算法计算得到，可以加速算法的运行．可以看出，文献［4］中的算法不再是针对每个轨迹点进行压缩，而是针对路段进行压缩．

例4 最短路径算法．原始轨迹如图5（a）所示，由L1到L99条路段构成，红色箭头表示实际行驶的路径．我们把原始轨迹分解成几段子轨迹，并保证每条子轨迹都尽可能长．从L1开始，到L2边是最短路径，则继续考虑L3，从L1到L3走的是最短路径，那么L2可以省略．继续考虑L4，L5，L6，直到L7，发现从L1到L7不是最短路径，第一条子路径寻找结束．第一条子路径为｛L1，L6｝，可以表示从L1到L6这部分轨迹．从L6开始考虑剩余的边，用｛L6，L9｝表示后半段的轨迹．因此，最终的压缩轨迹如图5（b）所示，为｛L1，L6，L9｝．

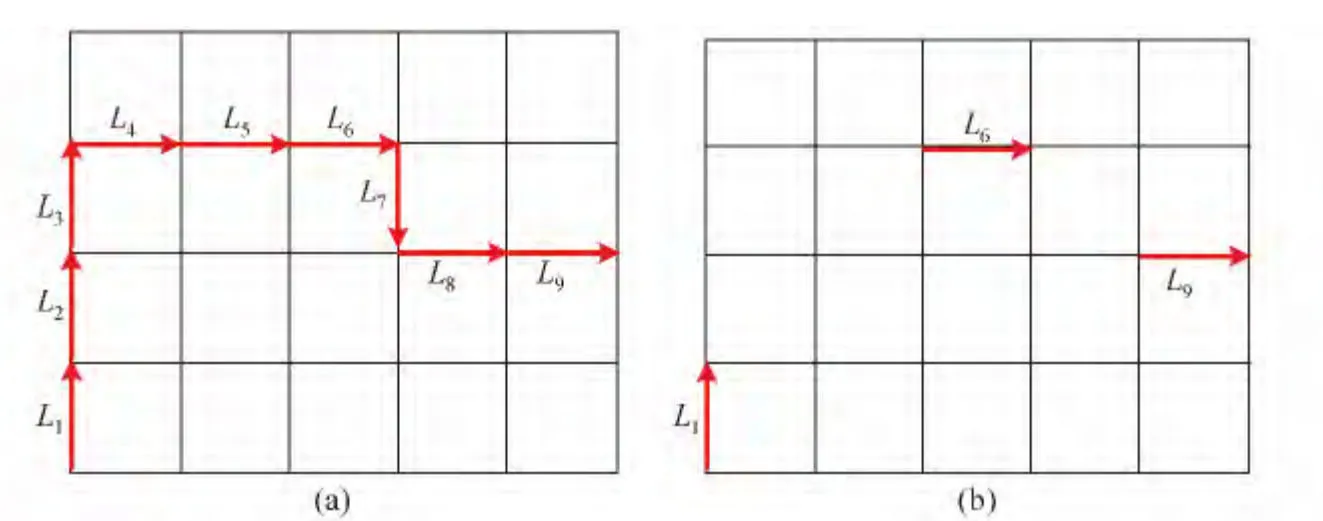
图5 最短路径算法Fig．5 Shortest path algorithm

文献［4］中的方法是用边的序列来表示轨迹，并通过最短路径和最小转角算法来减少边的数目，从而压缩数据．但是用边来代替轨迹点的一个缺点是，丢失了时间、速度的信息和详细经纬度的值．我们只能知道在某段时间内移动物体在某个路段上，而在这条路段上是如何运动的、在时间点物体处于路段的哪个位置，我们却无从知晓．

文献［5－6］把轨迹压缩问题转变为函数最优化的问题，目标是寻找一条最合适的轨迹，保证压缩率尽可能高，并且近似轨迹与原始轨迹相似度尽可能高．文章借用最小描述长度模型（Minimal Description Length，MDL），来最优化压缩率和相似度组成的目标函数．MDL模型是信息论中的常用模型，有两个部分组成，分别是L（H）和L（D｜H）·L（H）表示假设条件；L（D｜H）表示在此假设条件下，数据的描述情况．在数据压缩中，L（H）表示压缩后的轨迹；L（D｜H）表示近似轨迹与原始轨迹之间的误差．根据MDL原则，要找到一条路径，使得L（H）＋L（D｜H）最小，那么这条路径就是满足目标的路径．相关公式是

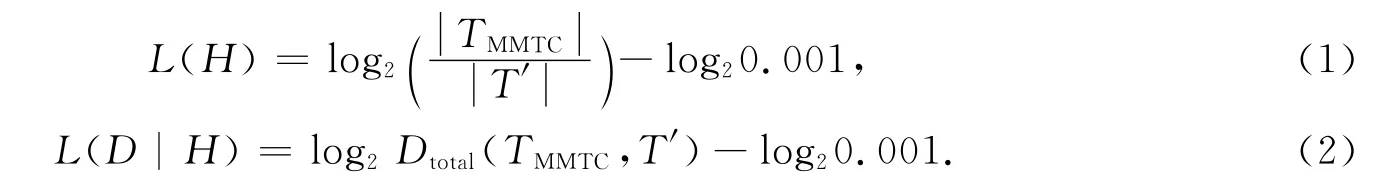
根据公式（1）、（2）计算L（H）和L（D｜H）的值，MDL＝L（H）＋L（D｜H）·其中，是压缩后的轨迹的长度，T′是Map－Matched后的轨迹，Dtotal（TMMTC，T′）是指TMMTC和T′之间的距离．压缩算法如下描述：从T′的起点p1开始，把后面的点都遍历一遍，找到p1与pi之间的最短路径SP1i，计算T′1i和SP1i之间的MDL1i，找出使MDL1i最小的i值．用SP1i来近似替代T′1i．然后从pi开始，重复上述步骤，直到轨迹的终点．把找到的所有SPij合在一起便是最终的TMMTC．可以看出，找到p1与pi之间的最短路径是要在路网上进行的，我们可以在预处理阶段计算出两两点之间的最短路径，保存在内存中，可以节省轨迹压缩的时间．该算法支持高频率的采样数据集和稀疏的路网结构，若是轨迹数据的采样率较低或者是路网结构密集的情况，该算法的效果不佳．另外，对于有环路的轨迹，该算法会直接忽略环，造成很大的误差．

城市的每个路段上的车流量是不一样的，一些交通要道使用的频率明显更高，而一些郊区小路的使用频率会低很多．文献［7］利用道路上的轨迹分布不均匀的信息，把轨迹分解为几段子轨迹，频率越高的子轨迹，就用越短的编码来表示．这也是哈夫曼编码的基本思想．文章把空间数据和时间数据分开，因为相同类型的数据分别压缩，可以做到更好的压缩率．对于空间数据，把GPS点映射到路段上，用最短路径压缩（Shortest Path Compression）的思想，省略中间的边，达到压缩的目的；用一部分数据集进行训练，找到频繁的子轨迹；然后把刚刚压缩过一次的轨迹，根据之前训练得到的频繁子轨迹进行分解；最后使用哈夫曼编码进行编码，原始轨迹最后转化为0和1的字符串表达．空间数据压缩是无损的，因为压缩后的轨迹与原始轨迹经过的是同一条路径．对于时间数据的压缩，文章使用了有损压缩，提出了TSND（Time Synchronized Network Distance）和NSTD（Network Synchronized Time Difference）两个误差度量，把时间压缩的误差控制在设定的TSND阈值和NSTD阈值以下．对于查询的支持，文章通过空间数据和时间数据的解压缩，然后合并来完成．

基于路网结构的压缩技术利用静态的路网结构来描述动态的数据，能显著减小存储空间．但是缺陷也是由于静态的路网结构不容易更新，从而灵活性不够．其次，与经纬度类似地，人们不能直接理解路段数据．另外，基于路段的轨迹不能直接使用，需要解压缩后才能支持查询，从而查询性能变低．

综上，对轨迹压缩算法进行总结，结果如表1所示．

表1 轨迹压缩算法总结Tab．1 Summary of trajectory algorithm

1．3 语义压缩方法

原始轨迹和路网轨迹尽管能很好地记录移动物体的运动踪迹，但是对于人们理解轨迹的含义却帮助不大．人们阅读轨迹时，无法明白一组经纬度坐标代表的意义．因此文献［11－12］介绍了语义轨迹，用POI、标志物、路口和路段来表示车辆的行驶过程，人们阅读语义轨迹时，能明确知道轨迹的起点、终点以及行驶经过的路段．

文献［9－10］认为只要保存有意义的状态和事件就能大致表达出轨迹的运动状态，因此提出了语义轨迹压缩（Semantic Trajectory Compression，STC）．文章把一条轨迹拆分为各个事件，包括行驶的路段，如从边A直走到达边B，以及方向的改变，在B路口左转到达边C．这种描述方法，可以用一条边来表示若干个点，从而达到压缩的目的．显然这种方法的压缩和解压缩时间会比较长，并且原始的经纬度信息完全丢失，保留的只是物体的一部分运行状态，因此支持的LBS应用也是有限的．优点是压缩后的语义轨迹便于阅读，比原始的轨迹更容易理解．

在文献［21］中，作者提出了一种获取轨迹摘要的Partition－Summarization两步框架，认为已有的语义轨迹只包含位置的信息，而忽视了速度、方向这些信息．因此在文章中，作者提取了6个特征，包括道路等级、道路宽度、道路方向、速度、停车次数和U形转弯次数，来表示轨迹每一个阶段的特征．在Partition阶段，根据之前提取的6个特征，把轨迹切分为几段子轨迹，每段子轨迹内部具有相似的特征，而子轨迹与子轨迹之间的特征差异较大．在每段内，选取最具代表性的特征来描述这段的行驶过程．例如，轨迹从A点行驶到B点，速度超过平时速度的50%．在Summarization阶段，把每段以及每段内的特征合在一起，描述轨迹的行驶过程．文章提出的这种方法，提取了轨迹的概要，不仅压缩了数据量，而且也便于人们理解轨迹的行为．文献［22］描述了文献［21］对应的展示系统，要求输入一条原始轨迹序列，并输出一段描述性文字，大体描述了轨迹的行驶特征以及经过的重要位置．

语义压缩后得到的轨迹，便于人们阅读理解，并且显著地减少了空间开销．但缺点是丢失了具体的经纬度信息，从而不能支持具体的点查询．语义轨迹在支持的查询上的缺陷在第2节中有具体介绍．

2 压缩轨迹查询

历史轨迹在很多应用中有重要的作用，比如分析城市交通状况、预测人们的移动轨迹．而轨迹查询是必不可少的一个步骤．在本文中，我们把轨迹查询分为时空查询和空间关键字查询两类，并讨论压缩后的轨迹对这两类查询的支持情况．

在空间范围中，主要有3种形态的空间对象：点、区域和轨迹．轨迹查询就是通过评估空间对象之间的关系，并返回满足条件的空间对象，比如查询经过一个点的所有轨迹．然而，我们不仅要关注空间关系，还要关注时间约束．因此，轨迹查询是更多表示满足时空关系的查询．另外，随着语义信息也逐渐被应用在轨迹数据中，满足时空关系并且满足语义约束，是一种新型的查询．

2．1 时空查询

轨迹的时空查询关注的是空间对象的时空关系．根据空间对象的类别，文献［23］把轨迹时空查询分为P－查询（Points－Query）、R－查询（Regions－Query）和T－查询（Trajectories－Query）3类．

·P－查询：是指查询轨迹和点的时空关系，可以分为：①查询与一段轨迹满足一定时空关系的POI［24－26］，例如top－k最近邻查询；②查询与一个POI或一组POI满足一定时空关系的轨迹［27－29］，例如，给定一组POI，查询经过这些POI最近的所有轨迹．

·R－查询：是指查询轨迹和区域的时空关系，可以分为：①查询在指定时间段内经过某个区域的所有轨迹，这类查询可以分析城市的交通状况；②查询在指定时间段内轨迹经过的热点区域［30－31］．

·T－查询：是指查询轨迹与轨迹之间的时空关系，可以分为：①查询出轨迹数据库中的相似轨迹［30，32］，例如分析轨迹间是否具有相似子轨迹；②查询满足预先设定的距离阈值的轨迹，如何计算轨迹间的距离也是研究点之一．

2．2 空间关键字查询

随着POI的文本描述越来越普遍，实际应用也要求同时考虑文本描述和时空约束，例如查询经过加油站和火车站最近的一条轨迹．空间关键字查询是指，输入文本信息和时空约束条件，返回满足条件的空间对象．根据空间对象的不同，结合文献［33－34］，我们把轨迹关键字查询分为空间点关键字查询和轨迹关键字查询两类．

·空间点关键字查询：是指输入查询条件，返回满足条件的POI．

·轨迹关键字查询：是指输入查询条件，返回满足条件的空间轨迹．

百度地图、高德地图都支持空间关键字查询，例如查询当前位置周围的餐厅．在空间关键字查询中，有3类查询是主流查询，很多研究工作针对这些查询提出了各种索引结构［35－40］和查询算法．这3类查询分别是Boolean kNN Query（BkQ）［35］、Top－k kNN Query（TkQ）［36，38，41］和Boolean Range Query（BRQ）［42］．

·Boolean kNN Query：输入一组关键字q、一个（组）查询点p和整数k，查询返回k条轨迹包含所有的关键字，并且按照空间距离排序．

·Top－k kNN Query：输入一组关键字q、一个（组）空间点p和整数k，查询返回k条轨迹，按照空间距离以及关键字相关度的综合排序．

·Boolean Range Query：输入一组关键字q和一个（组）空间点p，查询返回所有的轨迹，这些轨迹经过所有的p，并且含有所有关键词q．

我们根据压缩后的轨迹能否支持上述查询，对压缩方法进行了比较，结果如表2所示．其中符号“√”表示压缩轨迹完全支持该类查询，符号“△”表示需要在数据上建立索引或结合其他数据集才能支持该类查询．

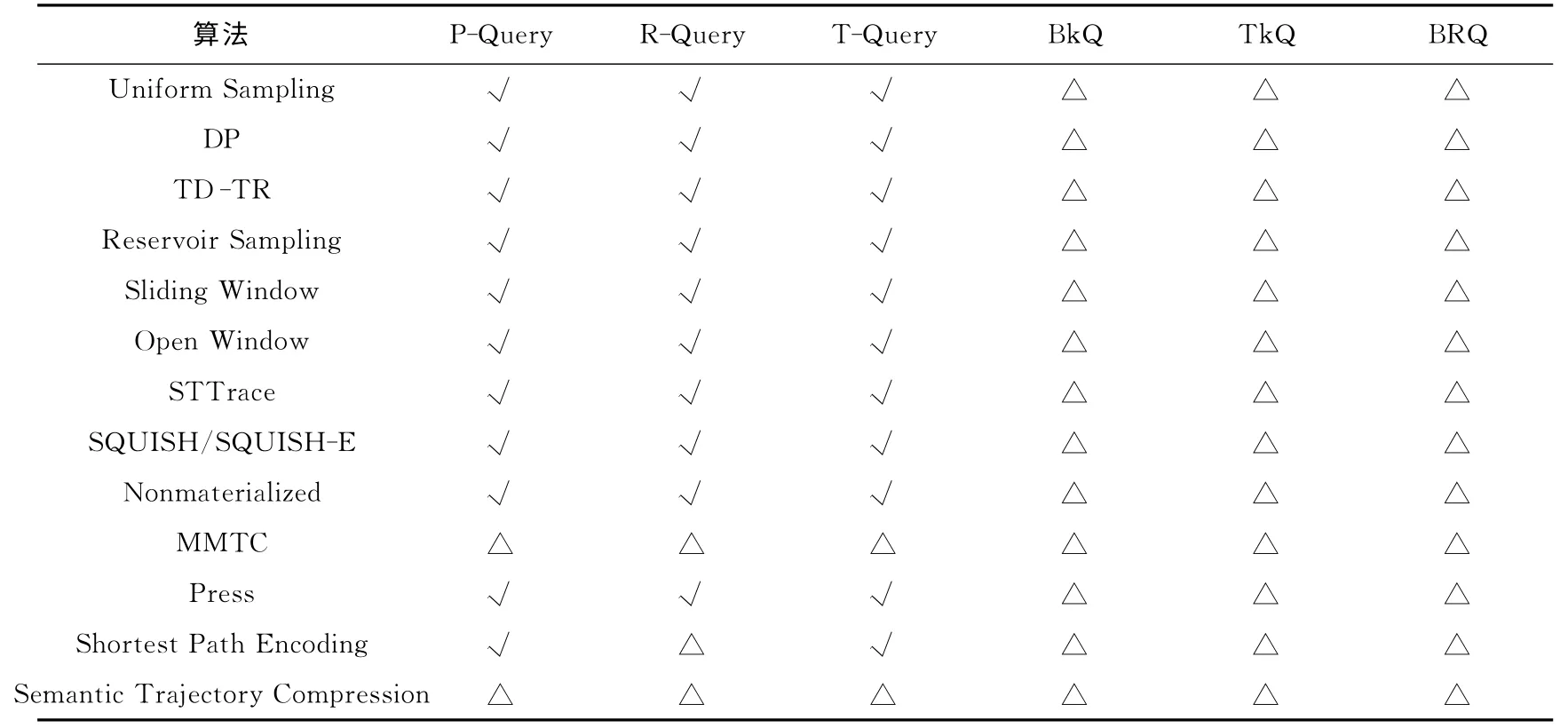
表2 压缩方法对查询的支持比较Tab．2 Comparison of existing compression methods

3 轨迹管理系统

轨迹管理系统需要对压缩轨迹进行管理，并建立索引来支持各种轨迹查询．本节主要介绍已有的轨迹管理系统．

文献［43－44］提出了TraStore系统，对数据的存储进行了优化．TraStore使用了动态的索引，把空间划分为网格，同一个网格内的轨迹存储在磁盘的一页上，这样可以有效减少读磁盘的次数．对于每个网格内的轨迹，TraStore进行了压缩，主要有两种压缩方法：一是无损的差分编码；二是有损的基于聚类的压缩方法．差分编码是指保留轨迹的第一个点，而从第二个点开始，把具体的经纬度值和时间都编码成相对于前一个点的差值，由于差值一般比较小，因此可以用更短的位数来保存，从而达到压缩的目的．基于聚类的压缩方法是指，把格子内的子轨迹段进行聚类，在每个类中，选取最具代表性的轨迹，进行保存．因此这种方法只保存了每个类中的代表轨迹，其余轨迹只保留了时间戳信息，删除了空间位置信息，因此是有损的压缩方法．

文献［45］提出的一种基于内存的列存储轨迹数据库SharkDB，大大提高了查询的速度．SharkDB把24个小时切分成以分钟为单位的列，并把轨迹的每个点根据时间戳归到每一列中．如果一条轨迹有超过一个点落在同一列中，则选取SED［14］最大的点保留，其余点则删除；如果一条轨迹没有点落在一列中，那么则使用直线模拟生成一个点，插入该列中．文章借助列存储的结构，对于列之间的数据，采用了差分编码，除了第一列外，后面的列只保存相对于前一列的差值，这样减小了数据量．

文献［21］提出了STMaker系统，即输入一条原始轨迹，输出一条语义压缩轨迹，保留了原始轨迹的重要位置点和行驶特征．STMaker先把原始轨迹转换为一条POI序列，然后把序列切分成不重叠的子轨迹段，使得每个子轨迹段内的特征相似．最终，用切分好的子轨迹段和行驶特征来描述轨迹．

文献［7］提出了轨迹压缩系统Press，认为由于轨迹分布的不均匀性，使用哈夫曼编码，把频率高的路段用较短的编码表示，而频率低的路段用较长的编码表示，最终把一条轨迹转换为编码的表现形式，从而达到较优的压缩率．应用时，轨迹需要先进行解码，消耗少量的时间．

集中式轨迹数据库在面对海量爆炸增长的轨迹时，尤其是更新频率很高并且实时查询要求很高时，其性能并不好．因此，分布式轨迹数据库成了一大研究热点．文献［46－49］分别提出的分布式存储框架、存储时空数据能高效地支持轨迹查询．文献［46］提出了分布式存储和查询的框架MD－HBase，对经度、维度和时间三维空间结构进行格子划分，然后使用Z－Order进行编码，以编码值作为HBase中的key，存储在HBase的region中．系统使用KD－Tree和Quad Tree为索引，加速查询．MD－HBase只支持Z－Order编码，而KD－Tree和Quad Tree索引对于高维数据的查询性能不高，因此在文献［47］中，作者提出了R－HBase的分布式存储和查询框架，建立R－Tree索引，能高效地支持高维数据；使用Hilbert曲线对空间进行编码，Hilbert曲线比Z－Order的优势在于能更好地支持查询本地性．MD－HBase和R－HBase都可以用于存储时空序列，通过切分格子和编码，使得查询尽可能本地化．文献［48－49］提出的SpatialHadoop是一种空间数据库，用于存储空间数据．SpatialHadoop增加了新的空间索引，并且索引适合MapReduce的运行环境．索引由全局索引和局部索引两部分组成．全局索引保存在主节点中，保存着数据在节点上的划分，可以支持网格文件、R－Tree和R＋－Tree等3种类型；而局部索引用于节点内部数据组织，在处理Map任务时，会根据局部索引，拆分文件，读入到内存中．SpatialHadoop能高效地支持范围查询、kNN和空间连接等3类空间操作．在查询阶段，MapReduce层利用全局索引修建文件块，得到文件块，再根据局部索引去获取分块中允许的记录，而不是循环遍历所有记录．

表3所示为以上几个轨迹数据管理系统的技术特点．

表3 轨迹管理系统Tab．3 Trajectory management system

4 总 结

对于爆炸式增长的轨迹数据，进行压缩是非常有必要的．数据压缩的目标有两个：一是降低数据量；二是降低轨迹之间的误差．第一个目标要求我们尽可能提高压缩率，第二个目标要求压缩后的数据与压缩前的数据尽可能相似．而这两个目标是相互矛盾的：压缩率越高，误差越大．因此，轨迹数据压缩需要平衡这两个目标．

已有的方法大致分为3类：线段简化压缩方法、基于路网结构的压缩方法和语义压缩方法．由于路网数据的成熟，基于路网的方法在近几年变得流行．把轨迹点序列用路段序列的形式表示，同时试图省略中间冗余的路段，是一般的解决思路．加入编码可以有效地提高压缩率．线段简化压缩方法的好处是由于保留了轨迹点的形式，因此压缩效率高，并且支持LBS应用时无需解压过程．线段简化方法的缺点是在欧氏空间内进行压缩，与移动物体的行驶轨迹不完全重合，因此固有的压缩方法本身就带有误差．语义压缩方法是结合路网数据或者POI数据集，转换得到POI的序列．语义轨迹的易读性使得它在一些应用中占据独到的优势．

未来的轨迹压缩研究重点主要有以下几个方面．

（1）语义轨迹压缩对于人们更易理解，如何查询语义轨迹是值得研究的方向．

（2）空间关键字查询中，已有工作并未考虑到时间约束，同时考虑时间约束和空间约束的轨迹关键字查询是未来的研究方向．

（3）管理语义轨迹的数据管理系统与普通的轨迹管理系统不同，设计高效的语义轨迹管理系统以及高效的索引结构值得探索．

（4）特殊的轨迹查询，例如在给定时间段内的最大速度，这一类查询不仅需要轨迹的时空信息，并且需要速度、方向的信息，所以在压缩轨迹时，应保留尽可能多的行驶特征．

（5）分布式轨迹管理系统以及内存轨迹数据库可以提高管理效率和查询性能，值得我们更多、更深入地研究．

［1］DOUGLAS D H，PEUCKER T K．Algorithms for the reduction of the number of points required to represent a digitized line or its caricature［J］．Cartographica：The International Journal for Geographic Information and Geovisualization，1973，10（2）：112－122．

［2］KEOGH E，CHU S，HART D，et al．An online algorithm for segmenting time series［C］／／Proceedings of the IEEE International Conference on Data Mining．IEEE，2001：289－296．

［3］POTAMIAS M，PATROUMPAS K，SELLIS T．Sampling trajectory streams with spatiotemporal criteria［C］／／Proceedings of the 18th IEEE International Conference on Scientific and Statistical Database Management．IEEE，2006：275－284．

［4］LERIN P M，YAMAMOTO D，Takahashi N．Encoding travel traces by using road networks and routing algorithms［M］／／Intelligent Interactive Multimedia：Systems and Services．Berlin：Springer，2012：233－243．

［5］KELLARIS G，PELEKIS N，THEODORIDIS Y．Trajectory compression under network constraints［M］／／Advances in Spatial and Temporal Databases．Berlin：Springer，2009：392－398．

［6］KELLARIS G，PELEKIS N，THEODORIDIS Y．Map－matched trajectory compression［J］．Journal of Systems and Software，2013，86（6）：1566－1579．

［7］SONG R，SUN W，ZHENG B，et al．PRESS：A novel framework of trajectory compression in road networks［C］／／Proceedings of the 40th International Conference on Very Large Data Bases．ACM，2014：1402－1546．

［8］MUCKELL J，HWANG J H，LAWSON C T，et al．Algorithms for compressing GPS trajectory data：An empirical evaluation［C］／／Proceedings of the 18th SIGSPATIAL International Conference on Advances in Geographic Information Systems．ACM，2010：402－405．

［9］SCHMID F，RICHTER K F，LAUBE P．Semantic trajectory compression［M］／／Advances in Spatial and Temporal Databases．Berlin：Springer，2009：411－416．

［10］RICHTER K F，SCHMID F，LAUBE P．Semantic trajectory compression：Representing urban movement in a nutshell［J］．Journal of Spatial Information Science，2014（4）：3－30．

［11］YAN Z，SPACCAPIETRA S．Towards semantic trajectory data analysis：A conceptual and computational approach［C］／／Proceedings of the International Conference on Very Large Data Bases PhD Workshop．2009：1－6．

［12］DAMIANI M L，SPACCAPIETRA S，PARENT C，et al．A conceptual view on trajectories［J］．Data and Knowledge Engineering，2008，65（1）：126－146．

［13］HERSHBERGER J E，SNOEYINK J．Speeding up the douglas－peucker line－simplification algorithm［M］／／International Symposium on Spatial Data Handling．Berlin：Springer，1992：134－143．

［14］MERATNIA N，ROLF A．Spatiotemporal compression techniques for moving point objects［M］／／Advances in Database Technology．Berlin：Springer，2004：765－782．

［15］LIU J，ZHAO K，SOMMER P，et al．Bounded quadrant system：Error－bounded trajectory compression on the go［C］／／Proceedings of the 31st IEEE International Conference on Data Engineering．IEEE，2015：987－998．

［16］MUCKELL J，HWANG J H，PATIL V，et al．SQUISH：An online approach for GPS trajectory compression［C］／／Proceedings of the 2nd International Conference on Computing for Geospatial Research and Applications．ACM，2011：1－8．

［17］MUCKELL J，OLSEN P W，HWANG J H，et al．Compression of trajectory data：A comprehensive evaluation and new approach［J］．Geoinformatica，2014，18（3）：435－460．

［18］BRAKATSOULAS S，PFOSER D，SALAS R，et al．On map－matching vehicle tracking data［C］／／Proceedings of the 31st International Conference on Very Large Data Bases．ACM，2005：853－864．

［19］HU C，WOLFSON O．Nonmaterialized motion information in transport networks［C］／／Proceedings of the 10th International Conference on Database Theory．2005：173－188．

［20］YIN H，WOLFSON O．A weight－based map matching method in moving objects databases［C］／／Proceedings of the IEEE International Conference on Scientific and Statistical Database Management．IEEE，2004：437－438．

［21］SU H，ZHENG K，ZENG K，et al．STMaker—A system to make sense of trajectory data［C］／／Proceedings of the 40th International Conference on Very Large Data Bases．ACM，2014：1701－1704．

［22］SU H，ZHENG K，ZENG K，et al．Making sense of trajectory data：A partition－and－summarization approach［C］／／Proceedings of the 31st IEEE International Conference on Data Engineering．IEEE，2015：963－974．

［23］ZHENG Y，ZHOU X．Computing with Spatial Trajectories［M］．Berlin：Springer，2011．

［24］CHEN L，ÖZSU M T，ORIA V．Robust and fast similarity search for moving object trajectories［C］／／Proceedings of the 2005 ACM SIGMOD International Conference on Management of Data．ACM，2005：491－502．

［25］CHEN Z，SHEN H T，ZHOU X，et al．Monitoring path nearest neighbor in road networks［C］／／Proceedings of the 35th SIGMOD International Conference on Management of Data．2009：591－602．

［26］SHANG S，DENG K，XIE K．Best point detour query in road networks［C］／／Proceedings of the 18th SIGSPATIAL International Conference on Advances in Geographic Information Systems．ACM，2010：71－80．

［27］PFOSER D，JENSEN C S，THEODORIDIS Y．Novel approaches in query processing for moving object trajectories［C］／／Proceedings of the 26th International Conference on Very Large Data Bases．ACM，2000：395－406．

［28］FRENTZOS E，GRATSIAS K，PELEKIS N，et al．Algorithms for nearest neighbor search on moving object trajectories［J］．Geoinformatica，2007，11（2）：159－193．

［29］CHEN Z，SHEN H T，ZHOU X，et al．Searching trajectories by locations：An efficiency study［C］／／Proceedings of the 2010 ACM SIGMOD International Conference on Management of data．ACM，2010：255－266．

［30］LEE J G，HAN J，WHANG K Y．Trajectory clustering：A partition－and－group framework［C］／／Proceedings of the 2007 ACM SIGMOD International Conference on Management of Data．ACM，2007：593－604．

［31］JEUNG H，YIU M L，ZHOU X F，et al．Discovery of convoys in trajectory databases［C］／／Proceedings of the 34th International Conference on Very Large Data Bases．ACM，2008：1068－1080．

［32］LEE J，HAN J，LI X，et al．TraClass：Trajectory classification using hierarchical region－based and trajecorybased clustering［C］／／Proceedings of the 34th International Conference on Very Large Data Bases．2008：1081－1094．

［33］CONG G，LU H，OOI B C，et al．Efficient spatial keyword search in trajectory databases［R／OL］．arXiv：1205．2880v1．

［34］CHEN L，CONG G，JENSEN C S，et al．Spatial keyword query processing：An experimental evaluation［C］／／Proceedings of the 39th International Conference on Very Large Data Bases．ACM，2013：217－228．

［35］CARY A，WOLFSON O，RISHE N．Efficient and scalable method for processing top－k spatial boolean queries［M］／／Scientific and Statistical Database Management．Heidelberg：Springer，2010：87－95．

［36］CONG G，JENSEN C S，WU D．Efficient retrieval of the top－k most relevant spatial web objects［C］／／Proceedings of the 35th International Conference on Very Large Data Bases．ACM，2009：337－348．

［37］LI Z，LEE K C K，ZHENG B，et al．An efficient index for geographic document search［J］．IEEE Transactions on Knowledge and Data Engineering，2011，23（4）：585－599．

［38］WU D，MAN L Y，CONG G，et al．Joint top－k spatial keyword query processing［J］．IEEE Transactions on Knowledge and Data Engineering，2012，24（10）：1989－1903．

［39］KHODAEI A，SHAHABI C，LI C．Hybrid indexing and seamless ranking of spatial and textual features of web documents［J］．Lecture Notes in Computer Science，2010：450－466．

［40］VAID S，JONES C B，JOHO H，et al．Spatio－textual indexing for geographical search on the web［C］／／Proceedings of the 9th Symposium on Spatial and Temporal Databases．2005：218－235．

［41］WU D，YIU M L，JENSEN C S，et al．Efficient continuously moving top－k spatial keyword query processing［C］／／Proceedings of the 27th International Conference on Data Engineering．2011：541－552．

［42］ZHOU Y，XIE X，WANG C，et al．Hybrid index structures for location－based web search［C］／／Proceedings of the 14th ACM international conference on Information and Knowledge Management．ACM，2005：155－162．

［43］CUDRE－MAUROUX P，WU E，MADDEN S．TrajStore：An adaptive storage system for very large trajectory data sets［C］／／Proceedings of the 26th IEEE International Conference on Data Engineering．IEEE，2010：109－120．

［44］WU E，CUDRE－MAUROUX P，MADDEN S．Demonstration of the trajStore system［C］／／Proceedings of the 35th International Conference on Very Large Data Bases．ACM，2009：1554－1557．

［45］WANG H，ZHENG K，XU J，et al．Sharkdb：An in－memory column－oriented trajectory storage［C］／／Proceedings of the 23rd ACM International Conference on Conference on Information and Knowledge Management．ACM，2014：1409－1418．

［46］NISHIMURA S，DAS S，AGRAWAL D，et al．MD－HBase：A scalable multi－dimensional data infrastructure for location aware services［C］／／Proceedings of the 12th IEEE International Conference on Mobile Data Management．IEEE，2011：7－16．

［47］HUANG S，WANG B，ZHU J Y，et al．R－HBase：A multi－dimensional indexing framework for cloud computing environment［C］／／Proceedings of the 14th IEEE International Conference on Data Mining Workshops．IEEE，2014：569－574．

［48］ELDAWY A，MOKBEL M F．A demonstration of SpatialHadoop：An efficient mapReduce framework for spatial data［J］．Proceedings of the 39th International Conference on Very Large Data Bases．ACM，2013：1230－1233．

［49］ELDAWY A．SpatialHadoop：Towards flexible and scalable spatial processing using mapreduce［C］／／Proceedings of the SIGMOD PhD Symposium．ACM，2014：46－50．