基于7方向Box样条的等值面可视化
(杭州电子科技大学计算机学院,浙江 杭州310018)
0 引 言
目前三维体数据场的可视化方法主要包括完整的数据场可视化和等值面可视化,后者又分为以移动立方体方法为代表的基于曲面表示的面绘制和基于光线投射算法的等值面绘制,基于表示的面绘制主要是为了建立离散体数据的分片线性模型方便体数据分析。大多数已有方法都是基于三线性插值,追求绘制效率但损失了质量,且体数据网格点梯度需要预计算并存储,资源消耗较大,梯度计算采用中心差分法,连续性差,导致绘制质量不高。为了解决这一问题,可采用体数据的高阶插值模型用于求交和梯度计算,如三三次B样条[1],一定程度上提高了绘制质量,但由于多项式次数高达9次,计算量太大。本文针对传统的基于光线投射算法的等值面绘制的缺陷,提出基于7方向Box样条的等值面可视化改进方法。采用文献[2]提出的4次C2连续的7方向Box样条为重建核进行拟插值,使重建后的模型具有三三次B样条(9次)相同的连续阶,不仅次数较低,且具有更好的各向同性性质,因而在对角平面的重建精度更高,减少沿轴向的瑕疵,另外求值速度也比三三次B样条高20%以上。
1 基于Box样条的重建
本文采用光线投射算法来实现可视化,并采用基于7方向Box样条拟插值模型进行求值和属性计算,下面详细介绍这种拟插值方法,并给出光线投射算法中需要用到的微分运算公式,另外为了提高求值计算的稳定性和效率,论文采用了7方向Box样条的BB形式,为了提高拟插值精度,本文增加了对体数据的预处理算子。
1.1 Box样条定义
Box样条是由s维空间Rs中的n个向量确定的,其中n ≥s,一般定义为一个s维n列的矩阵Ξ =[ξ1,ξ2,…,ξn],Ξ ∈Rs。该矩阵Ξ所表示的Box样条定义如下:
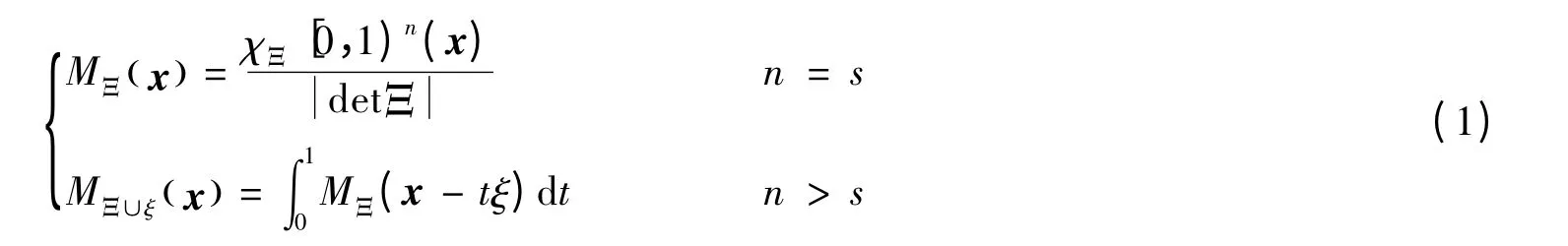
式中,Ξ[0,1)n是Rs中由Ξ的列向量所生成的多面体,χΞ[0,1)n(x)是定义在该多面体上的特征函数。7方向Box样条的详细理论参见文献[2-3],其对应的方向向量矩阵Ξ为:
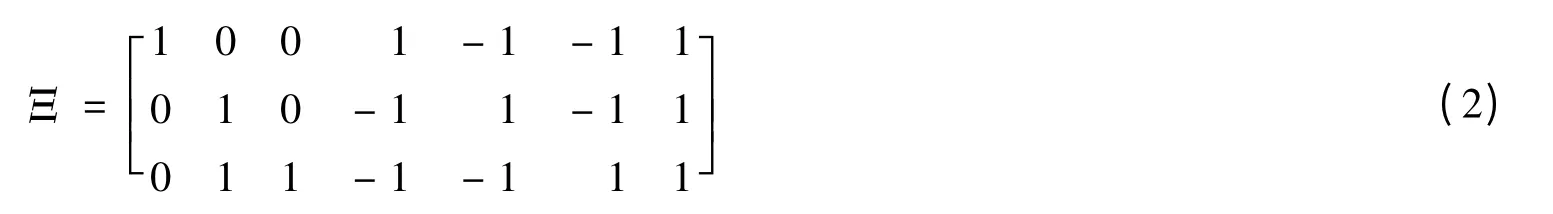
1.2 体数据重建
通常情况下,基于Box样条的拟插值函数如下式表示[4]:

一般情况下,μ可取为Dirac 泛函δ:f(s)af(0),可得出如下所示的拟插值结果:

根据文献[5]的结果,将μ 假定为一个微分算子多项式来提高精度,I是恒等算子,Δ是Laplace算子。是离散化Laplace算子,得到:

7方向Box样条基函数的支集是被截断了的十二面体形式,为了数据结构的方便性和高效性,可以把它的支撑加以扩展放到一个立方体[-5/2,5/2]3内部,接着就把这个立方体陪分成5×5×5×24个四面体,MΞ(x)在任意一个四面体内部都能够表示成4次多项式的形式,即:

其中,s=[x+0.5]决定了x所位于的单位立方体,而由=x-s 确定的x所位于的四面体的由r(1 ≤r ≤24)表示是s,r中的控制顶点表示伯恩斯坦多项式,其中a、b、c与d的和是4,w 则代表~x 在四面体r中的重心坐标。这样可以转化为BB形式,将式(5)记为:

式中,i =[x+0.5]确定x所在的立方体,(-2,-2,-2)≤s ≤(2,2,2)遍历局部的那些5×5×5 =125个立方体。重心坐标w与单位立方体s是互不相关的,它仅跟r 相关,参照式(6),整理得到F(x)在任意一个四面体内部具有的BB形式为:

1.3 体数据连续模型上的微分运算
在基于光线投射算法的等值面绘制过程中,采用体数据属性值和梯度幅值相结合的办法来设置传输函数,其中涉及到体数据模型上的微分运算,如梯度、曲率等,而对已建立的7方向Box样条拟插值模型来说,这些计算颇具优势,计算是精确的,又由于该模型已具备了BB形式,微分运算效率也较高。根据式(7),F(x)沿着x方向的导数如下:

根据文献[5]的结果,将两个6方向Box样条相减得出的差即为F(x)沿x方向的导数,通过化简得:
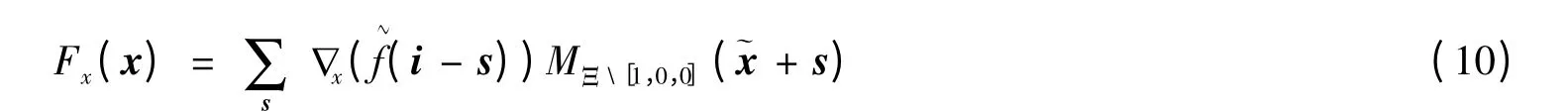
其中,(-2,-2,-2)≤s ≤(1,2,2),∇x是沿着x方向的差分算子。式(10)表示先通过差分把原数据变成差分场,然后再采用一个6方向的Box样条重建就可求得F(x)的导数,因此该运算可采取求值计算的同一流程,只需要调用不同的系数矩阵即可。曲率计算涉及的二阶偏导也类似,这样等值面上任意位置的第一和第二基本型的系数(E,F,G,e,f,g)很容易计算,由此可根据各种形式曲率的计算公式直接计算,比如Gauss 曲率为:

2 改进的基于光线投射算法的等值面可视化
Levoy 在1988年提出光线投射(Ray casting)算法,其根本任务是将离散分布的三维体数据映射为二维屏幕图像,由于绘制效果较好,它被广泛应用于医学、气象学、地质学等诸多领域,详细介绍可参考文献[6],其中重采样、设计传输函数和图像融合是3个关键步骤,本文研究等值面绘制,在数据融合阶段直接采用重采样的等值面交点颜色值为最终二维屏幕图像像素值,本文对传统算法的改进体现在前两个步骤,一是重采样阶段运用7方向Box样条拟插值模型的标量值计算来提高采样点精度,二是传输函数设计采用体数据属性值结合梯度幅值的方式,改进颜色映射效果,且属性值和梯度幅值仍然在7方向Box样条拟插值模型上进行精确计算,进一步提高图像质量。重采样和设计传输函数的详细描述如下:
1)给定一个等值面的阈值,沿着视口的方向上任意一个像素点投射的光线穿越待重建物体,,然后取固定的步长值对体数据进行重采样,利用式(8)计算出相邻的两个重采样点的标量值,并分别减去阈值,若得到的结果符号相反便说明必然有一个光线跟当前等值面相交,继续利用式(8)在两采样点间迭代计算直至满足精度要求,确定交点坐标,由视口上求得的全部的交点构成了该重建物体处于给定阈值所对应的离散等值面。与传统方法采用的三线性插值比较,重采样点的标量值计算精度高,从而提高了光线与等值面交点的准确度。
2)抽取出等值面之后就可对等值面着色。本文的着色通过传输函数实现,通常着色是对一定的属性值设置一定的颜色区域,然后根据RGB 颜色索引表建立1 维传输函数,最后将属性值映射为颜色。得到的颜色一般均是伪彩色,可依据不同需求设置不同颜色值,本文使用这种传输函数可视化等值面误差,如图1所示。为得到更好的等值面曲率可视化效果,本文又提出了属性值结合梯度幅值的颜色映射。以高斯曲率为例,首先根据计算梯度幅值,其中一阶导利用式(10)进行计算,再根据式(11)计算高斯曲率,本文设计的传输函数分两步完成,首先将属性值和梯度幅值规范化后分别映射为色相和亮度值,饱和度设置为用户参数,默认值取较好的经验值0.7,然后将HSV模型转换为RGB模型,从而得到最终图像的颜色值。与传统的采用中心差分法比较,梯度幅值精度高得多,在三线性插值方法基础上估计曲率则难以得到可靠的结果,曲率计算也是精确的,从而为等值面上的曲率可视化提供了可能。
3 实验结果
由于7方向Box样条具有C2连续性,基于光线投射算法的等值面绘制过程中体数据标量值、梯度和曲率的计算在拟插值模型的基础上精确的,为了验证本文方法重建等值面的精度优势,本文选用根据Marschner-Lobb 函数采样得到的体数据进行测试,采样规模为41×41×41,取等值面阈值为100,得到的可视化结果见图1,其中误差的颜色映射为1 维的传输函数,从误差大于等于0.075 到误差等于0的等距划分。图1(a)为三线性插值得到的等值面可视化结果,图1(b)给出了根据参数方程密集采样得到的数据集等值面绘制结果,可视为精确结果,图1(c)为本文方法等值面可视化结果,颜色映射为重建误差,通过比较可以看出,本文的方法误差明显优于三线性插值方法,并与图1(b)较为接近。

图1 不同方法等值面重建误差可视化结果
图2给出了本文的方法重建等值面高斯曲率的可视化绘制结果,传输函数采用曲率结合梯度幅值分两步设计的方法,得到了很好的等值面曲率图像。图2(a)中Bucky数据集分辨率是32×32×32,等值面阈值是30;图2(b)中Fuel数据集分辨率是64×64×64,等值面阈值是20;图2(c)中Hydrogen数据集分辨率是128×128×128,等值面阈值是30。

图2 本文算法的等值面高斯曲率可视化结果
各类算法绘制耗时对比如表1所示。由表1可知本文算法耗时比三三次插值短,比三线性插值算法长,这是因为本文是基于连续模型的而三线性插值算法是基于离散模型的。为了更好地绘制,需要找到耗时与精确度的平衡点,耗时可通过软、硬件提高,故本文算法还是比较好的。
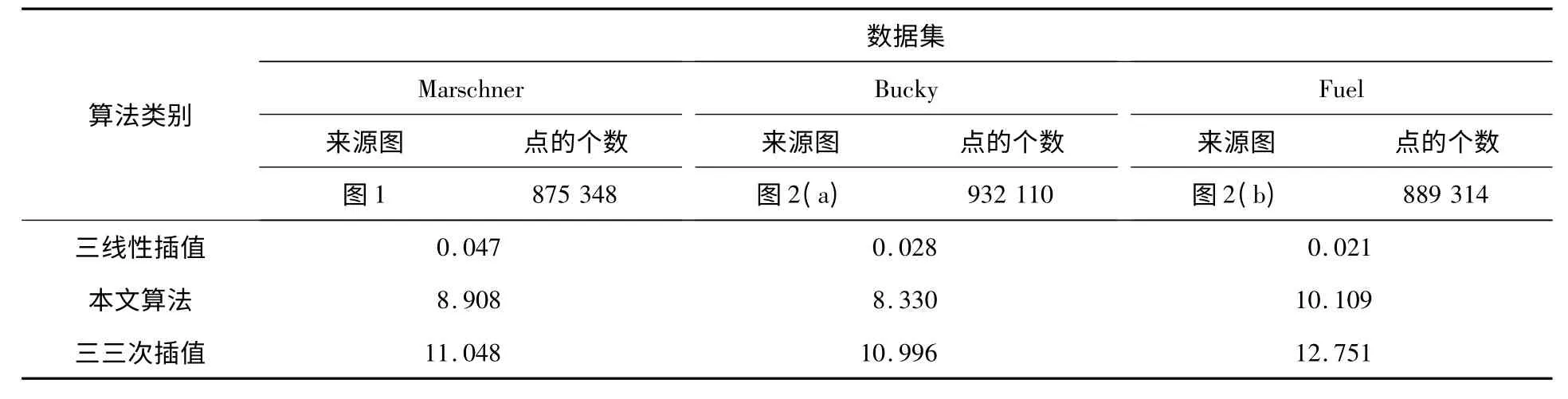
表1 算法耗时对比表s
4 结束语
本文利用7方向Box样条拟插值用于求交和属性计算,因其为分片四次多项式基函数,因此标量值计算比传统的三线性插值精度高得多,它的全局C2连续性使梯度、曲率的计算都很精确,因此大大地提高了绘制质量。采用连续模型的不足在于计算效率不高,尽管已采取办法使得本文比三三次B样条计算速度快,但总体速度仍有待提高,因此今后将进一步研究适合GPU 加速的7方向Box样条求值算法,并结合到基于GPU的光线投射算法中去。
[1]Xu Y,Yu G,Guan L.Tri-cubic polynomial natural spline interpolation for scattered data[J].Calcolo,2012,49(2):127-148.
[2]Entezari A,Möller T.Extensions of the Zwart-Powell box spline for volumetric data reconstruction on the Cartesian lattice[J].Visualization and Computer Graphics,IEEE Transactions on,2006,12(5):1337-1344.
[3]Peters J,Reif U.Subdivision surfaces[M].Berlin:Springer Berlin Heidelberg,2008:57-81.
[4]Fang M E,Lu J,Peng Q S.Volumetric Data Modeling and Analysis Based on Seven-directional Box Spline[J].Science China Information Sciences,2012,57(6):1-14.
[5]De Boor C,Höllig K.B-splines from parallelepipeds[J].Journal d'Analyse Mathématique,1982,42(1):99-115.
[6]Gamito M N,Maddock S C.Ray casting implicit fractal surfaces with reduced affine arithmetic[J].The Visual Computer,2007,23(3):155-165.

