二次NURBS曲线的退化曲线

尹乐平， 张 跃， 朱春钢

(大连理工大学数学科学学院，辽宁 大连 116024)

二次NURBS曲线的退化曲线

尹乐平， 张 跃， 朱春钢

(大连理工大学数学科学学院，辽宁 大连 116024)

NURBS曲线是几何造型中广泛使用的曲线拟合工具。当某一权因子趋向于无穷时，NURBS曲线趋于相应的控制顶点，当所有权因子趋向于无穷时，其极限曲线的几何性质目前还没有结论。利用NURBS曲线的节点插入算法，将NURBS曲线转化为分段有理Bézier曲线，结合有理 Bézier曲线的退化理论，得到当所有权因子趋向于无穷时其退化曲线的几何结构。

NURBS曲线；有理Bézier曲线；toric退化

非均匀有理 B 样条(non-uniform rational B-spline，NURBS)方法是Bézier方法、B样条方法和有理Bézier方法的推广，它将这些造型技术表示的曲线曲面转化为统一的表示形式。同时，NURBS曲线拥有局部调整性、强凸包性、权因子交比性、节点插入算法、de Boor算法等具有深刻几何意义的性质及算法[1-2]。NURBS曲线还可以精确地表示初等解析曲面，便于将参数曲面与解析曲面转化为统一的模型进行处理。因此，NURBS方法广泛应用于工业几何设计，从而成为曲线曲面造型中最为流行的技术。

在曲线曲面造型设计中，NURBS曲线曲面的形状由其控制顶点与权因子所决定。文献[2]中给出了NURBS曲线权因子的几何意义和交比性质，以及某权因子发生改变时 NURBS曲线的几何性质。因此可以研究当所有权趋向于无穷时，NURBS曲线曲面的极限曲线曲面与控制顶点之间的关系。

2002年，Krasauskas[3]提出了参数域为凸多边形的一种多边形曲面——toric曲面，而有理Bézier曲线曲面是其特殊形式，其理论来源于toric簇与toric理想。Sturmfels[4]详细介绍了toric簇、toric理想与正则三角剖分的理论。Zhu[5]也给出了 toric簇、toric理想在正则分解上的退化形式。Garcia-Puente等[6]利用toric簇、toric理想以及 toric退化理论给出当所有权趋向于无穷时，toric曲面的退化曲面的几何意义。

对二次准均匀NURBS曲线，通过节点插入算法，当所有内部节点重数与 NURBS曲线次数相同时，曲线等价于分段有理Bézier曲线。在各段上应用有理Bézier曲线的退化理论[6]，得到当权趋于无穷时，NURBS曲线的退化曲线为每段有理 Bézier曲线退化的曲线之并，最后给出具体实例。

1 有理Bézier曲线及其退化曲线

首先给出传统意义下由 Bernstein基函数定义的有理Bézier曲线。

定义 1[1]. 给定 n+1个空间向量i=0,… ,n，称参数曲线段。

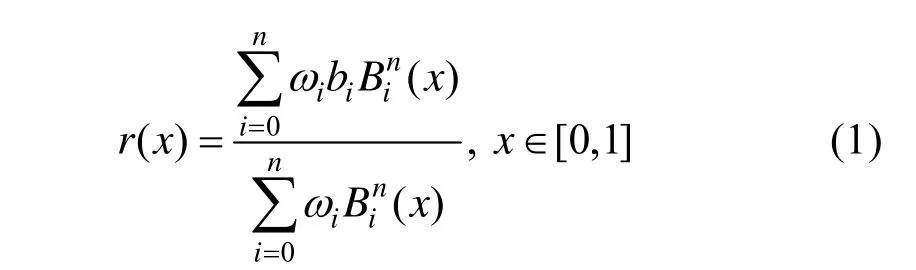
为一条n次有理Bézier曲线。其中：

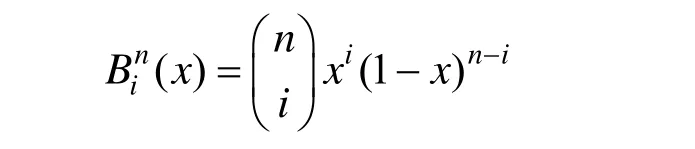
是n次Bernstein基函数， bi为控制顶点，ωi为权因子或权。用直线段依次连接相邻两个 bi所得的n边折线多边形称为控制多边形。

Krasauskas[3]定义的 toric曲面是有理 Bézier曲线在高维空间中的一种自然推广，在此对其定义进行简单介绍。

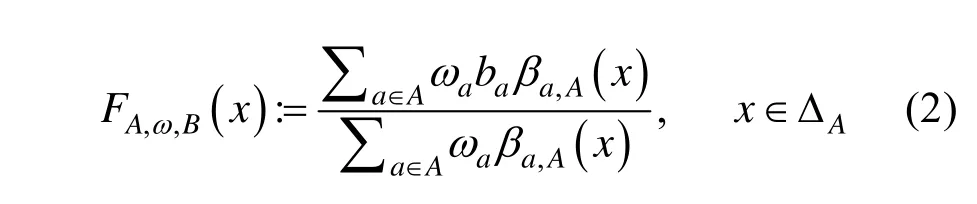
称为toricBézier曲面，其中toric基函数βa,A(x)为为常数。

当 toric曲面参数域取一维空间整数格点集时，控制顶点集 B ⊂ R3时，得到的参数曲线为参数变换下的有理Bézier曲线[3,6]。

l2(x)=n - x。对i∈ A，其toric基函数定义为：

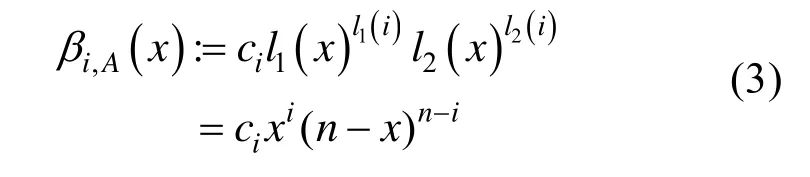
令控制顶点集B⊂R3，将 toric基函数式(3)代入表示toric Bézier曲面的式(2)中，得到：在式(3)中取x=ny， ci取为，toric基函数即为n次Bernstein基函数。

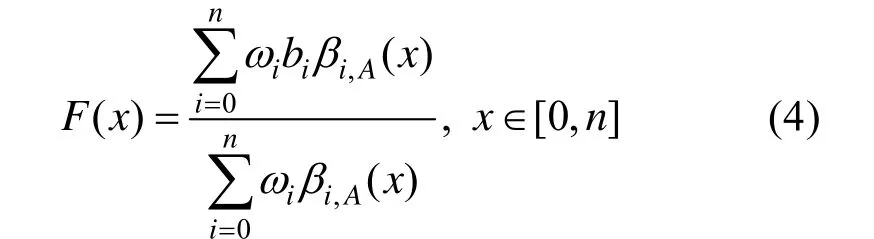
由此有理 Bézier曲线是式(4)中 toric Bézier曲线在简单参数变换下的特殊情况。因为参数变换并不影响曲线形状，为了方便讨论，本文后述所提到的有理Bézier曲线都是此表示形式。

为了给出有理Bézier曲线的退化形式，利用提升函数λ和给定的权定义带参数t的有理Bézier曲线：

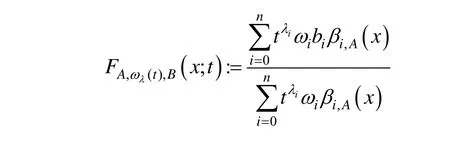
由如上定义，正则分解Sλ中的每一子集Sj中的格点集与相应的控制顶点与权，可定义一段有理Bézier曲线，记为Sλ中所有子集对应的有理 Bézier曲线之并称为由正则分解Sλ所诱导的正则控制曲线[6]，记为

定理1[6].

定理 1说明当所有权趋向于无穷时，有理Bézier曲线的退化曲线恰是其正则控制曲线。

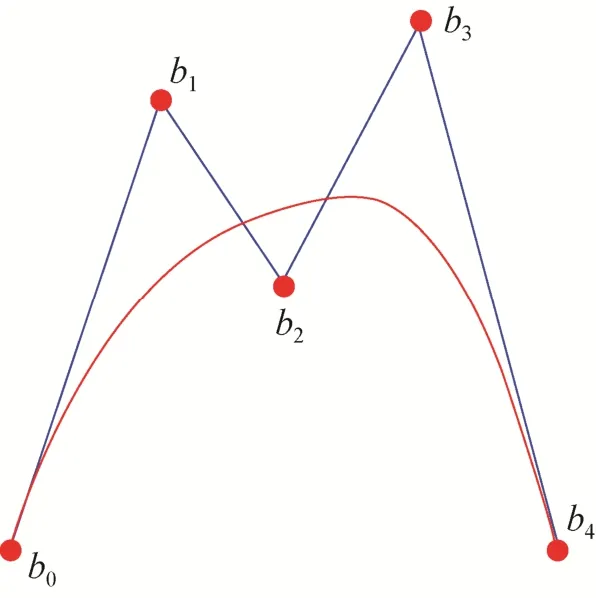
图1 四次有理Bézier曲线及控制多边形

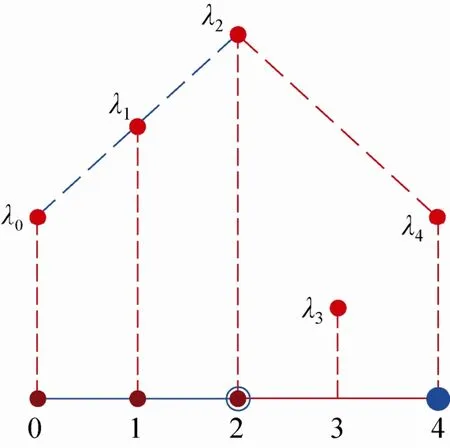
图2 提升函数λ对应的正则分解

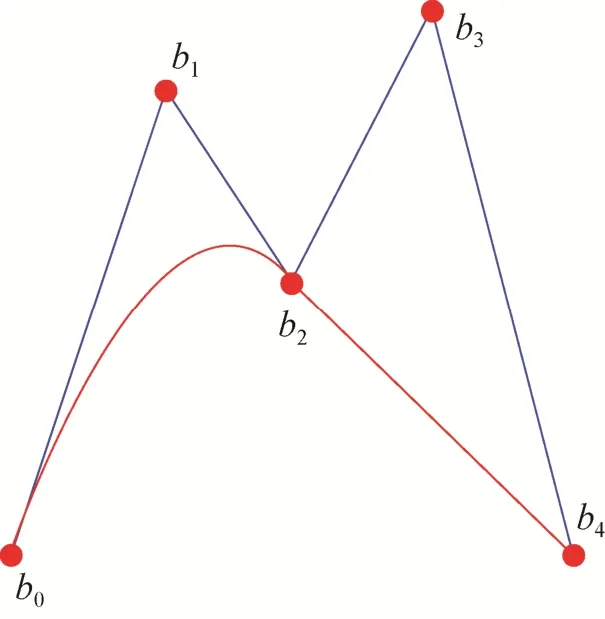
图3 提升函数λ诱导的正则控制曲线

2 NURBS曲线及其二次曲线的退化

2.1 NURBS曲线的定义及其节点插入算法

定义 2[2]. 参数曲线：

为了研究NURBS曲线的退化曲线，首先要建立NURBS曲线与有理Bézier曲线的联系，需应用NURBS曲线的节点插入算法，这一算法在NURBS曲线研究中具有重要意义。NURBS曲线节点插入算法所新生成的控制顶点和权不改变曲线形状，其算法思想如下[1-2]。Ni,p为定义在节点向量

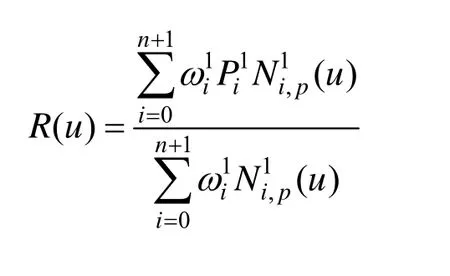
其中：

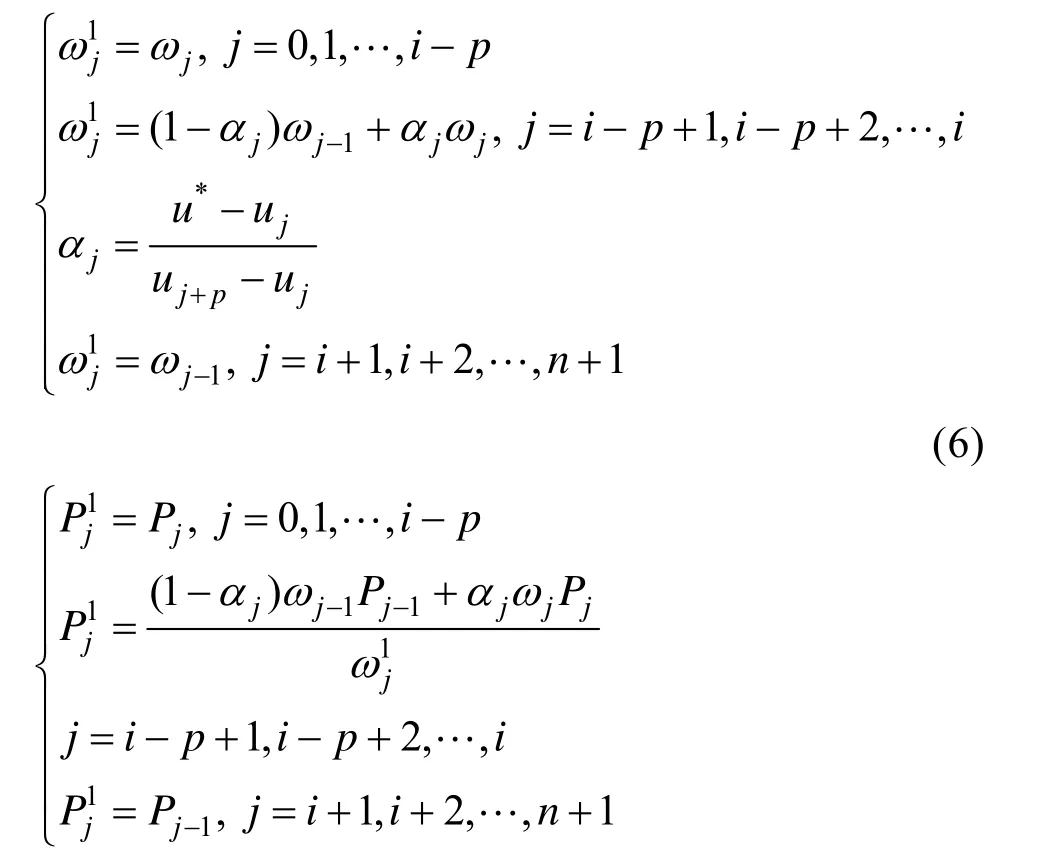
u0=u1=…=up，un+1=un+2=…=un+p+1，其节点满足ui=u0+(i- p)h(i= p+1,… ,n +1)，这时对应的p次NURBS曲线称为准均匀NURBS曲线。对p次准均匀NURBS曲线使用节点插入算法，使其内部节点 ui(i=p+1,…,n)的重数达到p重，则NURBS曲线在区间上为有理多项式曲线，经参数变换：

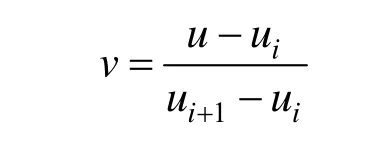
后为p次有理Bézier曲线。这样将NURBS曲线分割为 n - p+1段有理Bézier曲线。

2.2 二次NURBS曲线的退化

设二次准均匀 NURBS曲线的节点向量为U={0,0,0,1,2,… ,n -1,n,n,n}。由节点数与曲线次数的关系，曲线控制顶点个数为 n+ 2。设控制顶点集给定权为

对二次准均匀NURBS曲线，定义其控制顶点集P的提升函数μ：

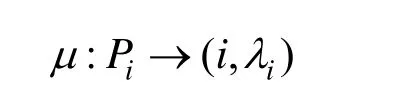
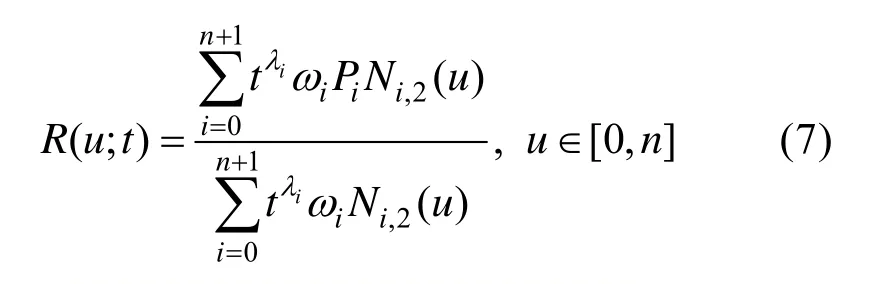
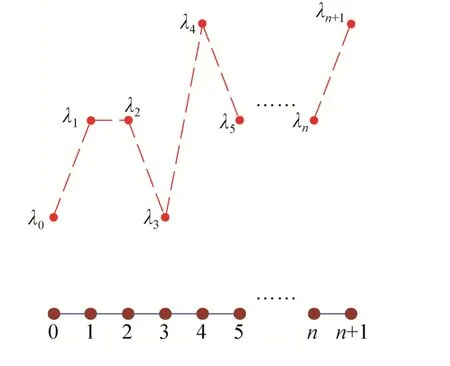
图4 提升函数μ

因为NURBS曲线插入节点的先后顺序与结果无关，不妨设每次插入的节点为 ui= i(i=1,2,… ,n -1)。每次插入节点后增加一个控制顶点与带参权，这样 n-1次插入节点后控制顶点集为原来的NURBS曲线可以表示为n段有理Bézier曲线之并，每段曲线的控制顶点集记为

入算法式(6)，则各组带参权之间满足关系：

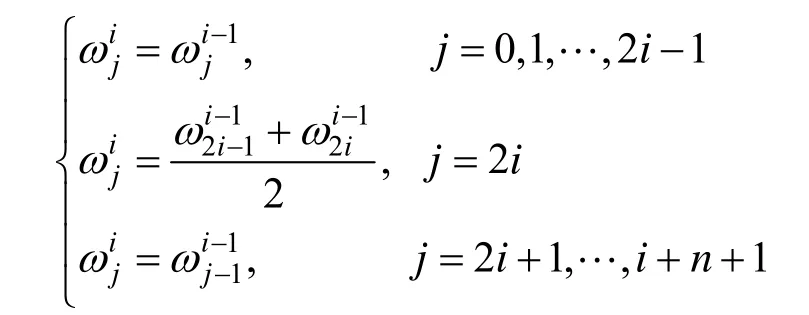
由上式可得节点插入后新生成的带参权为原来相邻两权的线性组合，且与原来带参权的关系为：

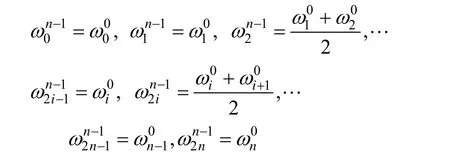
其中i=1,2,…,n-1。各组控制顶点满足关系：

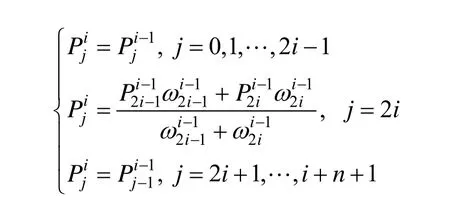
可得与原来控制顶点满足关系：

其中，i=1,2,… ,n -1。

这样将原来的 NURBS曲线分成n段二次有理Bézier曲线，第i段(i=2,… ,n -1)对应的带参权及控制顶点为：

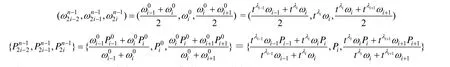
第i段(i=2,… ,n -1)二次有理Bézier曲线形 式为：

当t→∞时，二次有理 Bézier曲线Ri(v;t)的退化曲线为由正则分解 Svi所定义的正则控制曲线，设为

定理2. 当t→∞时，准均匀二次NURBS曲线 R(u;t)的退化曲线为其正则控制曲线：

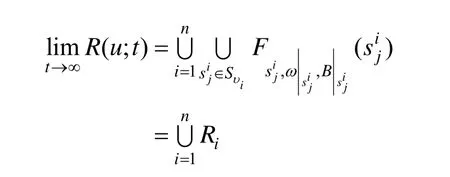
证明.利用 NURBS曲线节点插入算法式(6)将NURBS曲线式(7)分成n段二次有理Bézier曲线当t→∞时，给定提升函数μ，对节点插入算法中新生成的控制顶点的几何位置与带参权进行如下讨论：

(1)λi+1＞λi时，由则新生成控制顶点对应带参权为

(2)λi+1＜λi时，此时新生成控制顶点对应带参权为

(3)λi+1=λi时，新生成控制顶点对应带参权为

采用同样的方法，通过讨论λi-1，λi的大小关系，可以得到Ri(v;t)的另一端控制顶点当 t→∞时的位置与所对应的权。由此，当t→∞时，定义在[i - 1,i]上的二次有理Bézier曲线Ri(v;t)的控制顶点位置及权因子可以确定，其对应的提升为，设其诱导的正则分解为Svi，Svi的子集为。由定理1[6]，得到当t→∞时，ri(v;t)的退化曲线为其正则控制曲线而NURBS曲线 R(u;t)的退化曲线为每一段退化曲线的并集，定理得证。

3 实 例

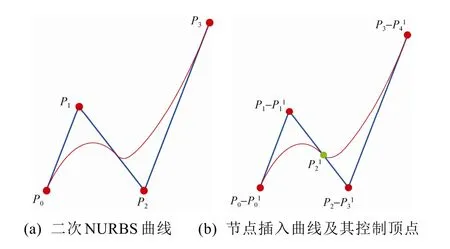
图5 NURBS曲线节点插入

对控制顶点定义提升函数 μ1，满足。则退化后的曲线为两段二次有理Bézier曲线退化曲线的并。由于λ1＞λ2，则前一段有理Bézier曲线退化为直线段，后一段有理Bézier曲线在提升下退化为控制顶点权为(0.75,2,5)的二次有理 Bézier曲线。因此当t→∞时，该NURBS曲线的退化曲线为如图 6(a)所示的正则控制曲线，曲线退化过程如图 6(b)～(d)所示，分别对应参数t取2，5，10。

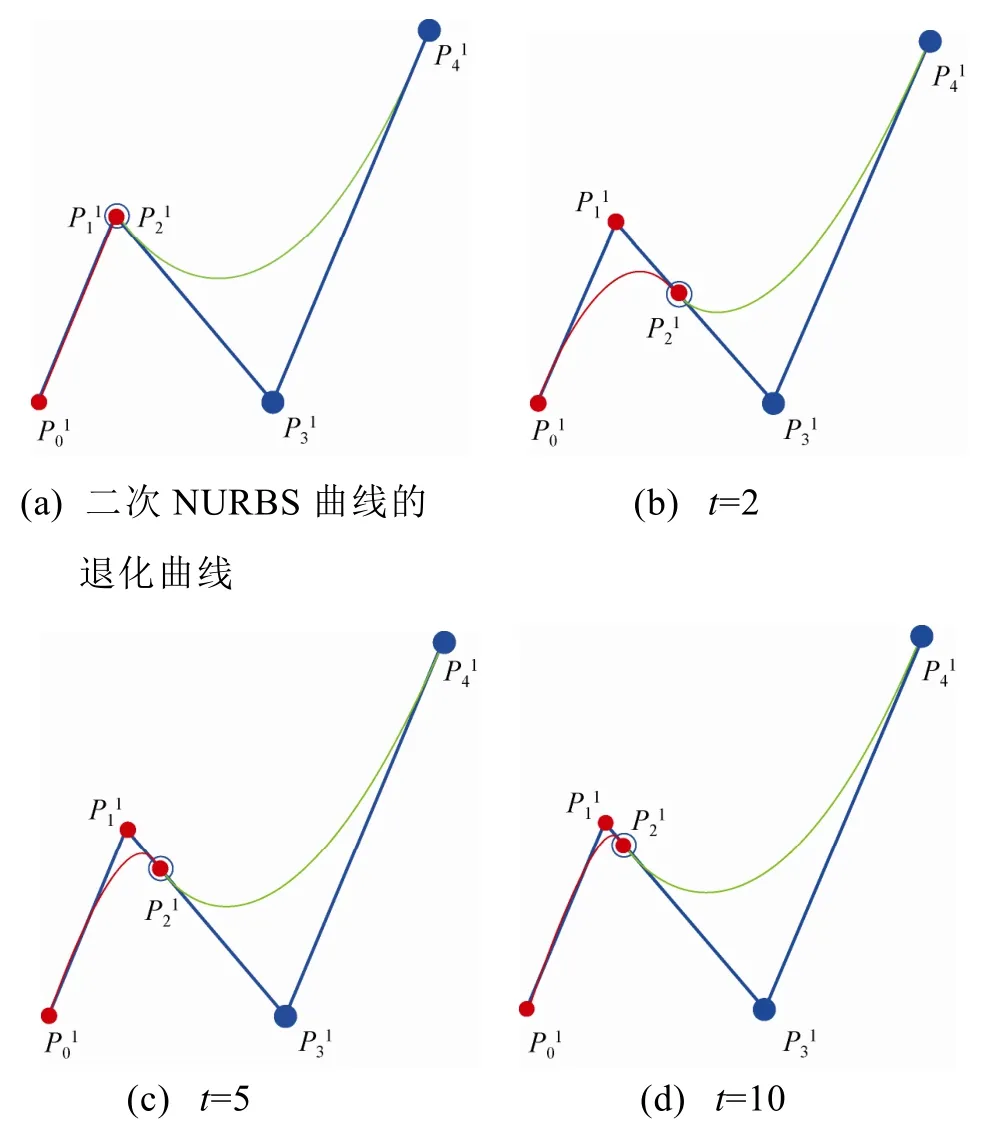
图6 二次NURBS曲线的退化过程

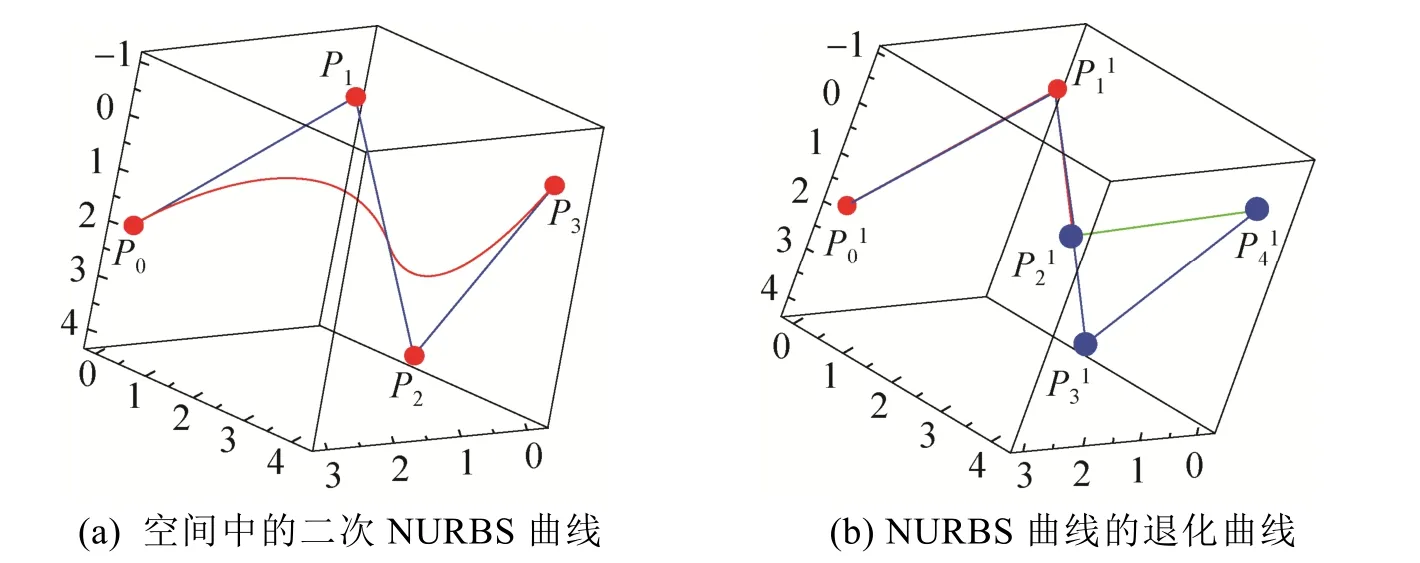
图7 二次NURBS曲线与其退化曲线

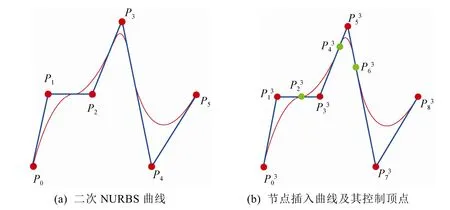
图8 NURBS曲线节点插入

图9 二次NURBS曲线的退化过程

4 总结与展望

本文中给出了二次准均匀NURBS曲线当权趋于无穷时的退化曲线。用同样的方法容易推出二次非均匀NURBS曲线与三次NURBS曲线的退化曲线。在以后的工作中，将研究高次NURBS曲线及NURBS曲面的退化形式。

[1] 王仁宏, 李崇君, 朱春钢. 计算几何教程[M]. 北京： 科学出版社, 2008： 242-249.

[2] Piegl L, Tiller W. The NURBS book [M]. 2nd ed. New York：Springer, 1997： 81-116.

[3] Krasauskas R. ToricSurface patches [J]. Advances in ComputationalMathematics, 2002, 17(1-2)： 89-113.

[4]Sturmfels B. Gröbner bases and convex polytopes [M]. Providence： AmericanMathematicalSociety, 1996： 63-73. [5] Zhu Chungang. Degenerations of toric ideals andtoric varieties [J]. Journal ofMathematical Analysis and Applications, 2012, 386(2)： 613-618.

[6] Garcia-Puente L D,Sottile F, Zhu Chungang. Toric degenerations of Bezier patches [J]. ACM Transactions on Graphics, 2011, 30(5)： 110.

Degenerations of Quadratic NURBS Curves

Yin Leping, Zhang Yue, Zhu Chungang
(School ofMathematicalSciences, Dalian University of Technology, Dalian Liaoning 116024, China)

NURBS curve, as a curve fitting tool, is widely used in geometricModeling. When a weight approaches to infinity, the limit of NURBS curve tends to corresponding control point. However, while all the weights tend to infinity, the degeneration of NURBS curve isStill unknown. In this paper, we converts the NURBS curve to piecewise rational Bézier curves by knot insertion algorithm and obtain the degeneration of NURBS curve while all the weights approach to infinity by using the degenerations of rational Bézier curves.

NURBS curve; rational Bézier curve; toric degeneration

TP 391

A

2095-302X(2015)02-0186-07

2014-10-08；定稿日期：2014-10-24

国家自然科学基金资助项目(11290143，11271060)；民用飞机专项资助项目(MJ-F-2012-04)；中央高校基本科研业务专项基金资助项目(DUT14YQ111)；辽宁省高等学校优秀人才支持计划资助项目(LJQ2014010)

尹乐平(1990–)，女，河北承德人，硕士研究生。主要研究方向为计算几何。E-mail：m13644089164@163.com

朱春钢(1977–)，男，北京人，教授，博士生导师。主要研究方向为计算几何。E-mail：cgzhu@dlut.edu.cn