热带气旋对海上风电支撑结构的影响研究*

庞 亮，徐 峰，龚 昕，战元福

（1.中国海洋大学，山东 青岛 266100；2.海洋石油工程股份有限公司设计公司，天津 300451）

随着现代社会的发展，能源与环境问题日益凸显。开发绿色新能源，成为科技界、工业界努力的重要方向。近几年来，人们对风能的利用逐渐增多。海上风电机组发电功率大又可减少噪音污染与景观破坏，是目前风能技术发展的趋势。

风力发电于20世纪中期得到发展。1956年Johannes Juul建造了里程碑式的Gedser风力机，成功与交流异步发电机连接［1］。1973年风力发电技术进一步发展，风电机的叶片数量、材料、形式不断改进，叶轮加大，塔架增高，直驱同步发电机开始应用。但是随之而来的风电机组噪声污染又成为需要解决的问题。目前风力发电又有从陆地转向近岸甚至深海发展的趋势。现在投入生产的海上风电机组是以固定式支撑结构为主。海上风电机组的支撑结构承受上部风轮结构重力以及风轮在海洋环境条件下产生的各种作用力，并且是承受风、浪、流、冰等环境荷载，保证风电机组结构安全的重要部分。值得指出的是，热带气旋或寒潮大风影响的海域，狂风、巨浪、暴潮等极端海洋气象因素的联合作用往往会导致结构的失效破坏，造成重大损失。

环境因素对结构作用的研究，大致可以分为环境荷载下结构动力响应机制研究［2－9］、结构模态参数识别技术及结构损伤诊断方法研究［10－11］、基于离散方法的结构动力分析模型和软件的开发研究［12－15］、基于动、静力分析的结构可靠性评估方法及结构优化设计研究等［16－17］。目前工程领域针对极端海况对海上风电机组影响方面的研究，大多借鉴海洋平台等结构设计规范的规定，基于年极值取样法选取工况组合对结构进行分析。海洋环境的简单选取往往造成工程设计标准偏低导致结构在极端海况作用下失效破坏或者过于保守导致不必要的资源浪费［6－7］。也有学者对于热带气旋对海岸工程以及风力发电工程的影响进行了区划式的分析［7，18－19］，但并未对极端天气过程对结构的作用机制作深入的研究。

本研究基于结构可靠度分析原理，建立结构响应模型、多维复合极值分布模型、灰色马尔科夫链模型嵌套的分析体系，进行热带气旋诱发海况对海上风力机组支撑结构作用的研究，以及风电支撑结构整体可靠度的初步分析。

1 双层概率分析模式

在热带气旋诱发的极端海况条件下对海上风电支撑结构进行可靠度分析时有两个问题需要解决：（1）样本缺乏。并非所有工程海域都有充分的热带气旋影响下的海况实测资料，同时结构在极端海况下的实测响应资料也难以得到。使得结构可靠性分析不易实现。（2）现有的结构可靠性分析方法不能充分考虑到全球气候变化、海平面升高带来的影响。

为解决上述问题，本研究采用数值模拟、概率分析、灰色预测方法交叉结合的研究手段，建立一个双层概率分析模式（Double-layer Probability Analysis Model-DPAM），第一层由灰色马尔科夫链预测模型和结构分析模型构成，第二层由结构分析模型与多维复合极值分布模型组成（见图1）。

1.1 灰色马尔可夫链预测模型

灰色模型（Grey Model-GM）是处理随机性强、信息量少的随机序列的有效方法［20－21］。最常用的灰色预测模型是一阶灰色模型GM（1，1），该模型由一元变量X的原始序列和生成序列构成。X（0）代表研究对象的实测值构成的序列（原始序列）：

图1 双层概率分析模式Fig.1 Double-layer probability analysis model

原始序列经一次累加处理（Accumulation Generating Operations-AGO），得到一阶生成序列X（1）：

由X（1）构造如下一阶微分函数：

其中a，u分别为发展参数和灰色参数。方程（1）的解为累加变量X（1）随时间变化的预测值：

则X（0）预测值为：

考虑到极端海况条件强烈的波动性、不规则性，需对GM（1，1）模型进行模型修正。本研究将灰色模型同灰色马尔科夫链模型（Grey Markov Chain Model-GMCM）相结合，提高模式的精确性。

在灰色马尔科夫链模型中，预测值与实测值间的残差（方程3）被分为不同状态，k步计算后，由状态i转为状态j的概率可由方程4计算：

式中：Mij（k）为状态i转为状态j所需步数，Mi是处于状态i的残差个数。最终建立状态转移概率矩阵（方程5）。修正后的预测值由方程6计算。

其中＝（δ1＋δ2）/2，δ2，δ1为不同状态的上下边界值。

1.2 多维复合极值分布模型

复合极值分布［22－25］是一种新型的联合概率分布模式，最早由刘德辅等提出。该分布由泊松分布与多维极值分布复合构成：

式中：F（λ；x1，x2，…，xn）代表多维复合极值分布函数；f代表每年台风发生的频次（泊松分布参数）；x1，x2，…，xn代表n维随机变量；F（x1）表示随机变量x1对应的边缘分布函数；f（x1，x2，…，xn）为多维极值分布的密度函数；Ω表示联合概率函数的定义域。

多维复合极值分布能够合理的反应由台风过程引发的极端海－气现象的概率特征。以该模式为基础对随机模拟法［23，26］进行的改进是针对受台风等天气过程影响海域的极端环境荷载分析的有效手段。

1.3 环境载荷模型

作用于海工结构的风载荷按下式计算：

式中：K为风荷载形状系数；Kz为海上风压高度变化系数；λ为基本风压；A为受压面积。基本风压P0按下式计算：

式中：α为风压系数，Vi为时距为t分钟的设计风速。

对小尺度圆形构件，垂直于其轴线方向单位长度上的波浪力f，当D/L≤0.2（D为圆形构件直径，m；L为设计波长，m）时，可按Morison公式计算：

式中：ρ为海水密度，CD为垂直于构件轴线的阻力系数，CM为惯性力系数，u为水质点相对于构件的垂直于构件轴线的速度分量，为水质点相对于构件的垂直于构件轴线的加速度分量。当只考虑海流作用时，圆形构件单位长度上的海流载荷fD按下式计算：

式中：CD为阻力系数，ρ为海水密度，UC为设计海流速度，A为单位长度构件垂直于海流方向的投影面积，设计海流速度采用平台使用期间可能出现的最大流速。

2 算例

本文以一座工作于中国南海大鹏湾的3MW三腿架式离岸风电系统为例，来分析台风对结构物的影响。工作环境水深约为24m。表1中列出基线风机总体性质，图2表示三脚架支撑结构的设计尺寸参数。

表1 风机参数Table 1 Wind turbine parameters

图2 三脚架风机支撑结构Fig.2 Tripod supporting structure of offshore wind turbine

2.1 运用GMCM方法预测极端海况

采用1954—1979年期间由台风过程的极值风速、波高及波浪周期的测量数据作为原始数列，建立AGO模型。运用GMCM计算1980—1999年期间预测值，并与同期测量数据比对。表2列出了在使用灰色模型预测台风引起的风速、波高及波浪周期时所需要的发展系数a及灰色输入系数u。之后运用马尔科夫链模型进行残差修正。修正后的预测数据与测量数据的比较如图3～5所示。不同变量的后验方差比C与小误差概率p也在表2中给出。计算结果表明，对于台风引发的极端海况因素的长期预测，GMCM是一种有效合理的模型。

表2 GMCM参数Table 2 Parameters of GMCM

图3 运用GMCM的风速预测Fig.3 Prediction of wind speed by GMCG

图4 运用GMCM的波高预测Fig.4 Prediction of wave height by GMCG

2.2 台风影响下三脚架式支持结构的响应

依据台风风速与GMCM预测波浪的结合进行结构物的静力分析和动力分析。由于缺少海流数据，使用原设计资料中提供的流速值代替台风过程相应海流值进行极端工况条件的计算。

图5 运用GMCM的波浪周期预测Fig.5 Prediction of wave period by GMCM

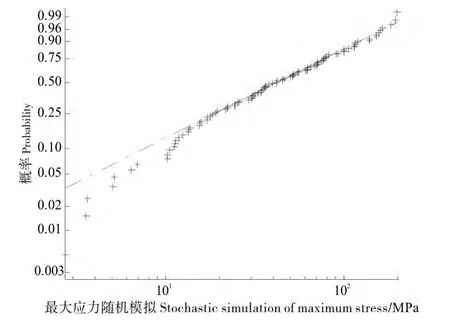
图6 台风导致的结构最大应力拟合Fig.6 Curve fitting of maximum stress values induced by typhoon

3 结语

图7 支撑结构的整体应力分布Fig.7 Integral stress distribution of the support structure

图8 支撑结构的局部应力分布Fig.8 Stress distribution of the local structure

海上风电设施工作环境较为恶劣，热带气旋对结构的影响不容忽视。灰色马尔科夫链模型适用于台风影响海域极端海洋环境条件预测，多维复合极值分布适用于进行极端海况以及结构响应的概率分析。本研究基于灰色马尔科夫链模型、多维复合极值分布模型和结构有限元模型构建了双层概率分析模式，是进行热带气旋对海上风电支撑结构影响分析的有效方法。

［1］Martin O L.Hansen.Aerodynamics of Wind Turbines ［M］.USA：Earthscan in the UK and USA，2008.

［3］Li H J，Wang S Q，Yang Y C，et al.Vibration characteristics of an offshore platform and its vibration control［J］.China Ocean Engineering，2002，16（4）：469-482.

［4］Li Huajun，Hu S L J，Jakubiak C.H-2active vibration control for offshore platform subjected to wave loading［J］.Journal of Sound and Vibration，2003，243（4）：709-724.

［5］Jonkman J M，Buhl M L.Loads Analysis of a Floating Offshore Wind Turbine Using Fully Coupled Simulation［C］.Los Angeles：Proc of Wind Power 2007Conference California，2007.

［6］Nielsen F G，Hanson T D，Skaare B.Integrated Dynamic Analysis of Floating Offshore Wind Turbines ［C］.Athens：Proc.Of EWEC 2006，2006.

［7］Andrew R.Henderson，Michiel B Zaaijer，Tim R Camp.Hydro-dynamic Loading on Offshore Wind Turbines ［C］.Naples：OWEMES Conference 2003，2003.

［8］Agarwal A K，Jain A K.Dynamic Behavior of offshore Spar platforms under regular sea waves［J］.Ocean Engineering，2003，30：487-516.

［9］Bhattacharyya S K，Sreekumar S，Idichandy V G.Coupled dynamics of SeaStar mini tension leg platform ［J］.Ocean Engineering，2003，30：709-737.

［10］Li Huajun，Wang Junrong，Sau-Lon James Hu.Using incomplete modal data for damage detection in offshore structures［J］.Ocean Engineering，2008，35：793-1799.

［11］Wang S Q，Li H J，Takayama T.Modal identification of offshore platforms using statistical method based on ERA ［J］.China O-cean Engineering，2005，19（2）：175-184.

［12］Φye S.FLEX4Simulation of Wind Turbine Dynamics［C］.USA：Proc of 28th IEA meeting，1996.

［13］Hansen A C.Users guide to the wind turbine dynamics computer programs YawDyn and AeroDyn for Adams Version11.0［R］.USA：University of Utah，1998.

［14］Jonkman J M.Dynamics Modeling and Loads Analysis of an Offshore Floating Wind Turbine［R］.Technical Report NREL/TP-500-41958，2007.

［15］Wayman E N，Sclavounos P D，Butterfield S，et al.Coupled Dynamic Modeling of Floating Wind Turbine Systems［C］.Houston：Offshore Technology Conference，2006.

［16］俞剑勇，张艳芳，王铭飞.海上风力发电工程钢结构疲劳分析［J］.钢结构，2008，23（110）：49-51.

［17］Sclavounos P D，Tracy C，Lee S.Floating Offshore Wind Turbines：Responses in a Sea state，Pareto Optimal Designs and Economic Assessment［C］.Lisbon：OMAE2008Conference，2008.

［18］欧进萍，段忠东，常亮.中国东南沿海重点城市台风危险性分析［J］.自然灾害学报，2002，11（4）：9-17.

［19］宋丽莉，毛慧琴，钱光明，刘爱君.热带气旋对风力发电的影响分析 ［J］.太阳能学报，2006，27（9）：961-965.

［20］Deng J L.Control Problems of Grey System ［J］.System and Control Letters，1982，5：288-294.

［21］Liu Defu，Jiang Hao，Pang Liang，et al.The Prediction Method of Typhoon Induced Extreme Sea Level in Southeast Coast of China［C］.Proc.of the ASME 28th International Conference on O-cean，USA：Offshore and Arctic Engineering，2009.

［22］Liu Defu.Long Term Distribution of Hurricane Characteristics［C］.Houston：Proc Offsh Tech Conf，OTC 4325，1982：305-313.

［23］Liu Defu，Song Yan，Shi Hongda，et al.Poisson-Logistic Compound Bivariate Extreme Distribution and Its Application for Designing of Platform Deck Clearance［C］.Cancun：Proc Offsh Mech Arc Eng，2003.

［24］Liu Defu，Pang Liang，Fu Gang，et al.Joint Probability Analysis of Hurricane Katrina 2005 ［C］.San Francisco：Proc Int Offsh Pol Eng Conf，2006，3：74-80.

［25］Pang Liang，Liu Defu，Yu Yifa，et al.Improved Stochastic Simulation Technique and Its Application to the Multivariate Probability Analysis of Typhoon Disaster［C］.Lisbon：Proc of 17th Intern Offshore ＆Polar Eng，2007，3：1800-1805.