涡激振动潮流能转换装置获能实验研究*

袁 鹏，陈东旺，王树杰，孙 飞

（中国海洋大学工程学院，山东省重点实验室，山东 青岛 266100）

相对于其它各种海洋能形式，潮流能作为一种相对容易开发的能源形式，近年来得到了较大的发展，主要利用能量转换装置把潮汐引起的海水往复运动产生的动能转化为装置运动部件的机械能，带动发电机发电。目前，潮流能发电形式主要是水轮机。考虑到中国的具体海洋环境，中国虽有长达5 000多公里的海岸线及较丰富的潮流能储藏量，根据统计，我国沿海地区130个可利用水道中的潮流能蕴藏量有13 948.5MW，大部分分布在浙江省、福建省沿海，如舟山地区某些水道，潮流的流速可以达到3m/s以上，但与世界上潮流能资源最好英国、挪威等国家相比，中国沿海的潮流总体上流速偏小，水深较浅。尤其是在中国的北方沿海地区，有相当多潮流流速在1.0m/s左右的海域。由于潮流能的能量密度与流速的立方成正比，因此在潮流流速较低的海域利用水轮机开发海流能，势必需要增大潮流能装置的尺度，对水深也提出了更高的要求，同时由于水轮机需要一定的起转流速，在流速较低时很难实现有效的能量转换，因此水轮机要在潮流流速大于1.5m/s时才能有较好的效益。这样一方面造成许多潮流能资源的浪费，也阻碍了潮流能利用技术在更大范围内推广。因此开发一种能够适合低流速下潮流能有效转换的装置，对于中国尤其是北方潮流流速偏低海域的潮流能开发具有重要意义。基于涡激振动原理的潮流能转换装置是一种新型的开发潮流能方式，在较低的流速情况下，可以将流体的动能高效地转化成潮流能转换装置的动能，继而转化成电能。出于以上考虑，有必要对利用涡激振动原理的潮流能转换装置进行研究［1－3］。

数十年来，学者和工程师们一直认为涡激振动是一种有害现象，当流体流过结构物在其后形成流场的泄涡频率与结构物的固有频率相近时引起共振，当振幅大到一定程度时则会引起结构物的损坏，因此对涡激振动研究的重点和目的在于如何减小涡激振动对于海洋立管、桥梁等结构物的负面影响，避免由此引起的疲劳破坏。然而，研究发现，在流速不高的情况下，可以产生很大的振幅，流体的动能大部分被振动体吸收，形成稳定的周期性振荡运动。将这一现象应用到潮流能转换装置中，通过有意识地引起和增强涡激振动，使潮流的动能转换为振动体振动的动能，从而实现潮流能的高效转换。美国密歇根大学最先提出了一种Vortex Induced Vibrations Aquatic Clean Energy（VIVACE）装置。它是一种基于涡激振动原理的潮流能转换装置，能将潮流水平流动的动能转化为其运动部件的横向振动，然后通过机械传动带动发电机发电。根据实验结果，该装置甚至可以在低于2knot的流速下发出电能，这意味着在全世界大多数有潮流的水道中都可以工作。这种装置如能得到广泛应用，将大大扩展可利用的潮流能资源范围，缓解能源紧缺问题。涡激振动原理的获能装置亦可以优化中国能源结构、促进清洁能源开发、应对气候变化、发展低碳经济等具有战略意义［4］。

本文从涡激振动潮流能转换装置发电原理研究出发，通过经验理论方法和实验的方法，研究涡激振动发电模型机在潮流中的水动力特性。

1 涡激振动原理

在均匀来流中，任何非流线型的物体浸没其中，会在物体的背流面形成交替泄放的漩涡，由于漩涡的泄放在物体表面产生不均匀的压强，进而物体受到流向和横向的脉动压力。此时如果物体的移动自由度大于零，则会在脉动压力的作用下诱发物体的周期性振荡。与此同时，物体的振荡运动又会改变边界剪切层分离点的位置，泄放的漩涡发生改变。漩涡作用在物体表面的压强产生变化，改变物体的振荡运动，将物体和流体间的相互耦合作用称为涡激振动［5］。

黏性流体遇到圆柱体时，阻滞效应导致流体与固体的边界层压力增大，沿着圆柱体迎流面向背面不断扩展。当流体惯性力占主导时，边界层会在截面径向位置最大处脱离圆柱体表面，此时在圆柱体表面分离点的剪切层速度为零，此后剪切层中靠近圆柱体的内层速度变的与来流方向相反。边界层在分离点脱离物体表面形成漩涡，继而向后伸展形成剪切层，剪切层间为尾流区，漩涡不断地在其中交替产生及泄放，漩涡泄放机理见图1。

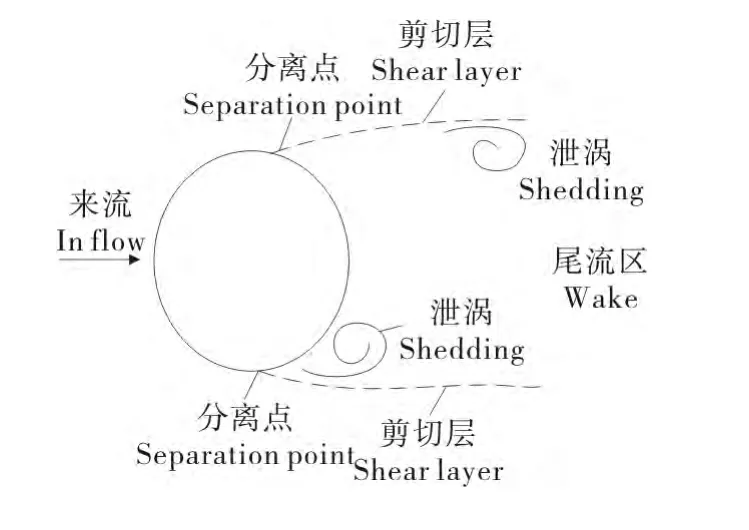
图1 漩涡泄放机理Fig.1 The principle of vortex shedding

由于剪切层内层速度小于剪切层的外层，因此便会诱导产生漩涡并且在两侧交替泄放，泄放的漩涡过程见图2。

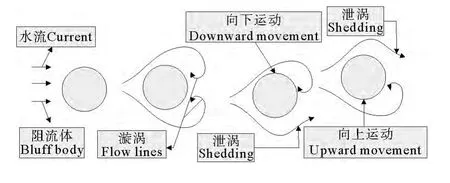
图2 漩涡泄放的过程Fig.2 The process of vortex shedding

2 涡激振动方程的建立

简化涡激振动原理潮流能发电实验模型结构，设圆柱的半径为D，长度为L，采用的弹承是弹性系数K为的拉伸弹簧，在水流速度为U的作用下在垂直于U的竖直平面上运动，结构简图见图3。

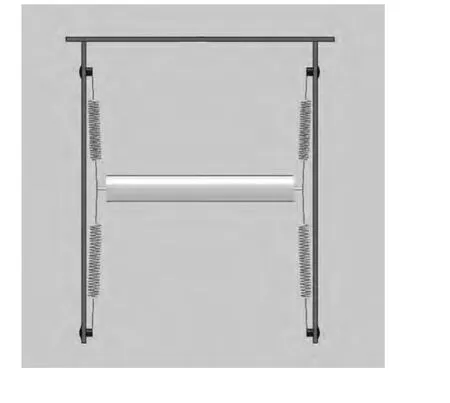
图3 涡激振动实验原理简图Fig.3 The model of VIV

振动微分方程可以表示为：

其中：Ms为质量；Cs为阻尼；Ks为弹性系数；FL（X）为流体升力；FD（X）为流体阻力；X为振动位移。

作用在圆柱体上总流体力的表达式也可以表示为：

其中：Cml是流体力系数惯性力分量；Cdl是其黏滞力分量；ω为振动响应圆周频率。

根据涡激振动理论，结构质量为振荡质量和附加质量的和。因此，可得到：

其中：m为振荡质量，包含圆柱体、振动部件、弹簧质量的1/3；ma为附加质量，可等效为排开流体的质量，从而可得结构的固有频率：

假设升力、阻力系数分别为CL，CD，因此得到升力FL与曳力FD如下：

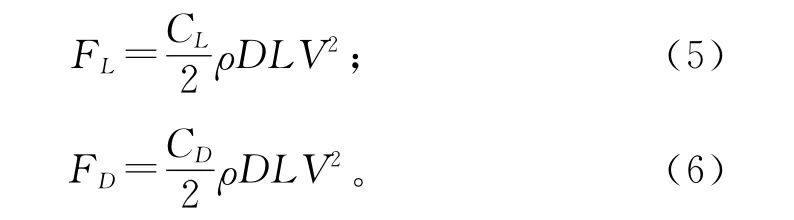
代入振动微分方程（1）可得：

代入微分方程（2）得：

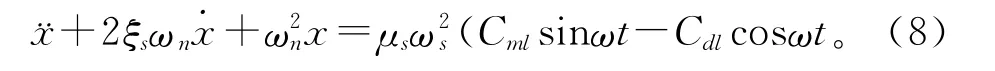
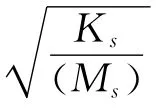
3 涡激振动方程的求解

在振动微分方程的求解过程中，升阻力系数的变化频率和结构振动频率是相同的，都是响应频率ω，由于存在升力与位移、反力与加速度之间的滞后，不同造成升阻力之间初始相位角的不同，设升力与圆柱体位移的相位角φ，反力与加速度之间的相位角φ1，则其升、阻力系数可表达为：

为了简化求解，假设其位移变化是简谐曲线，即：

将其代入微分方程（7）可得：

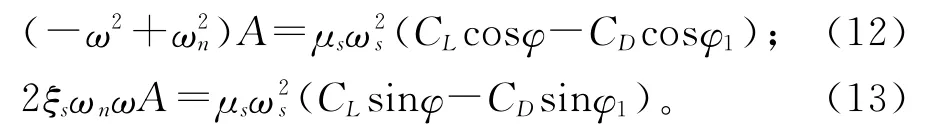
对于振动微分方程（8），同样为了简化求解，设结构的稳态响应位移为：

其中，力与圆柱体位移为－ε位移的初始相位。代入振动微分方程（6）中可得：

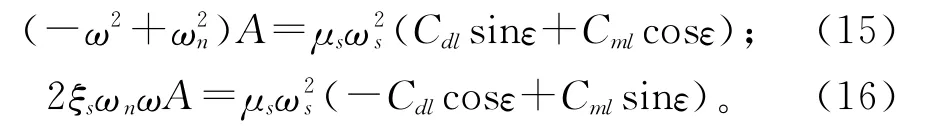
由上述（12）、（13）和（15）、（16）两个方程组得到φ、φ1、ε之间的数学关系，得到无量纲方程组：

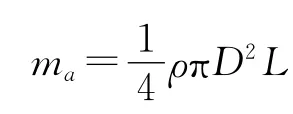
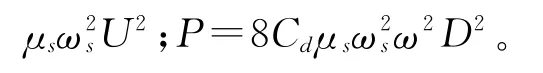
需要说明的是，本文侧重于Logistic回归模型的预测，因此将选取2010年前的地震数据共196组作为训练集，而将2010后的三次地震(2010年新西兰Darfield地震、2011年新西兰Christchurch地震以及2011年日本Tohoku地震)数据共57组作为测试集。根据前述Logistic回归方法利用训练集训练Logistic模型，然后将此模型应用于测试集，评估其预测效果。

4 预测模型的验证

实验1的振子直径D＝60mm，振子质量m＝0.337kg，弹簧刚度K＝23.8N/m，振子长度L＝0.22m，静水中振动系统固有频率fn，w＝0.688Hz。实验2的振子直径D＝60mm，振子质量m＝0.405 kg，弹簧刚度K＝23.8N/m，振子长度L＝0.22m，静水中振动系统固有频率fn，w＝0.672Hz。

根据上述数据，做出2组对比试验和预测模型的振幅比和频率比的对比图4～7如下：

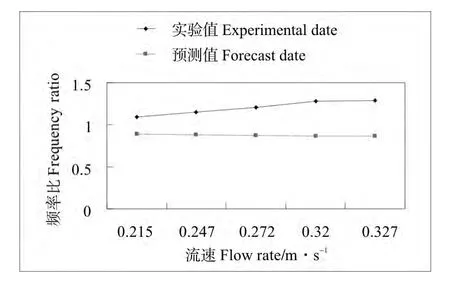
图4 实验数据1与预测数据1的频率比对比图Fig.4 The comparison chart of the experimental date and the forecast date on frequency ratio of the first test

图5 实验数据2与预测数据2的频率比对比图Fig.5 The comparison chart of the experimental date and the forecast date on frequency ratio of the second test

图6 实验数据1与预测数据1的振幅比对比Fig.6 The comparison chart of the experimental date and the forecast date on amplitude ratio of the first test

图7 实验数据2与预测数据2的振幅比对比图Fig.7 The comparison chart of the experimental date and the forecast date on amplitude ratio of the second test

由于涡激振动是1个非线性问题，频率比在±30%的误差范围内便会发生，因此，涡激振动预测模型具有一定的合理性，根据涡激振动预测模型对实验样机的部分数据进行指导和优化，设计制造了涡激振动模型样机，经过实验的验证，频率比在理论值误差的30%之内并且可以起振，预测模型具有可行性。

5 涡激振动数学耦合模型的建立

5.1 设计路线

根据实验室试验条件实际情况：水的流速最大可达到Umax＝0.75m/s，设计其共振的流速在V＝0.6 m/s左右，便于观察“锁定现象”周围流速的变化对振动的影响。关于振动有关参数的确定：在涡激振动的形成条件下，从雷诺数角度出发，根据生阻力系数图7所示，雷诺数范围内大约在TrSL2、TrSL3［6］区域左右出现升力系数的极值，其基本设计路线见图8。

图8 基本设计路线Fig.8 The basic design course

5.2 振子和弹簧的选择

目前选择5种不同直径的尼龙棒作为振子，侧板与振子打孔攻丝，两者采用螺杆连接，同时侧板与直线导轨机构的滑块采用螺钉连接。振子直径分别为40、55、70、85、100mm。

弹簧类型有5种，刚度参数分为5组：100、150、175、200、250N/m，通过弹簧的并联选择合适的有效刚度。

5.3 弹簧刚度选择依据

（1）计算雷诺数Re。雷诺数公式：Re＝U×D/ν。 （20）

在20℃时水的运动黏性系数为ν≈1×10－6m2/s。

（4）计算锁定现象振动频率f。在锁定区域，泄涡频率fs不再符合与斯特拉哈尔数S的线性关系，并且在折算速度Vr某一范围内，泄涡频率fs与振动系统的振动频率f保持一致，即f＝fs。

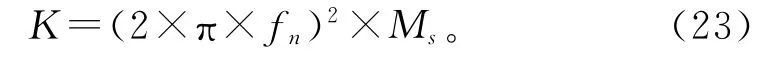
根据以上依据计算出各振子的最佳配合弹簧刚度：对于振子直径D＝40mm时，得到K＝591.61N/m，实验对应刚度值为：K＝500、550和600N/m；D＝55mm时，得到520.59N/m，实验对应刚度值为500、550、600 N/m；D＝70mm时，得到K＝390.44N/m，实验对应刚度值为：K＝350、400和450N/m；D＝85mm时，得到K＝335.07N/m，实验对应刚度值为：K＝250、300和350N/m；D＝100mm时，得到K＝373.221N/m，实验对应刚度值为：K＝300、350、400N/m。

由于流固耦合现象，频率比会在偏离1的情况下仍能具有较大的振动，同时实验条件参数等不确定性，选取了K＝250、275、300、350、400、450、500、550、600 N/m共9组弹簧。

6 涡激振动实验研究

涡激振动理论分析是在理想和简化运动的情况下对于涡激振动响应进行预测，为了验证涡激振动预测模型和涡激振动潮流能转化装置获能原理的耦合算法进行实验研究。

6.1 实验设备

采用上面所述的直径分别为40、55、70、85、100mm，长度均为375mm的5种振子和刚度分别为100、150、150、175、200、250N/m 的弹簧。通过弹簧间的并联选择合适的有效刚度，采用上面所述的9种弹簧刚度配合，弹簧刚度值在误差范围内取值。实验水池流速范围在0.4～0.75m/s间，实验地点为海工动力学实验室风浪流水槽，水槽参数为30m×1m×0.6 m。实验测量器材工具：测力计、游标卡尺、米尺、秒表、水流计。实验装置见图9。

6.2 实验数据

6.2.1 静水实验 在不同的振子和弹簧刚度组合下，得到振动系统在水中的自然频率fn，w，记录数据见表1。

6.2.2 流水实验 在不同振子和弹簧刚度组合下，得到各振子的起振流速和和达到最大振幅时的流速（见表2、3）。

图9 实验装置Fig.9 Experimental device

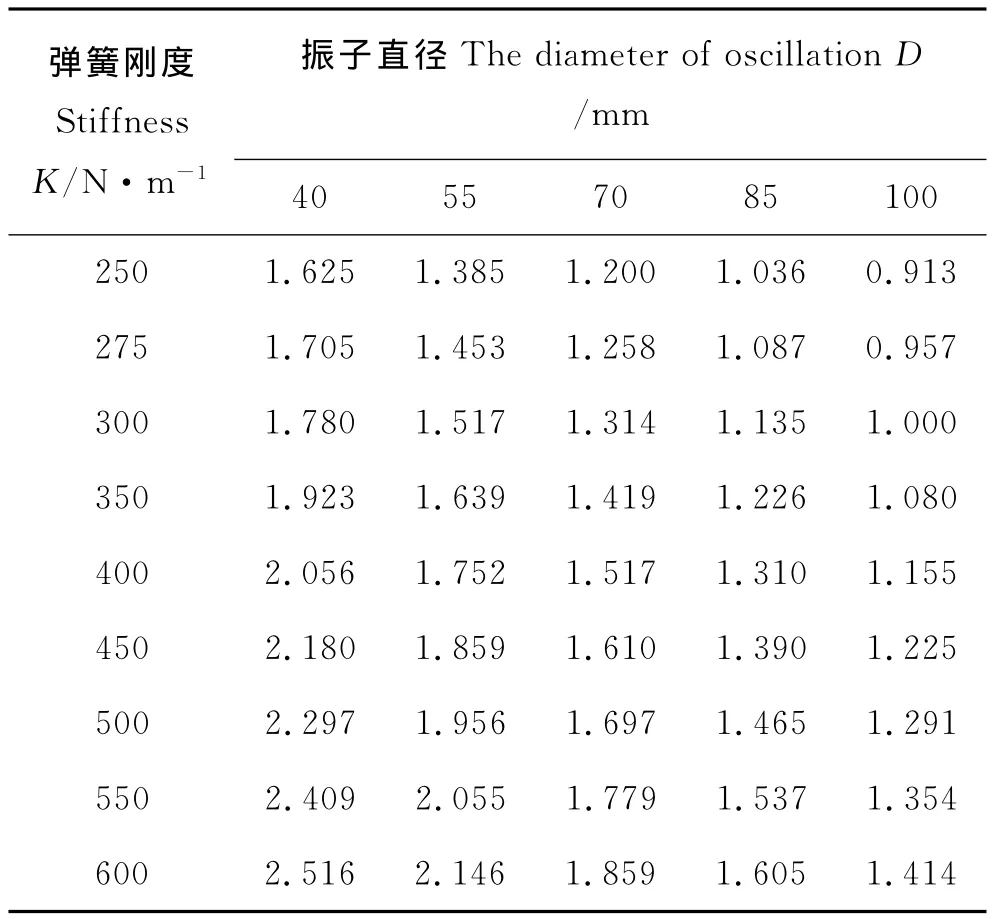
表1 不同的振子和弹簧刚度组合下振动系统水中自然频率（Hz）Table 1 The system of vibration′s natural frequency（Hz）under the combinationsof the different oscillation and different stiffness spring

表2 不同刚度下的起振流速Table 2 The start vibration′s flow rate under the combinationsof the different oscillation and different stiffness spring

表3 不同刚度下达到最大振幅的流速Table 3 The maximum amplitude′s flow rate under the combinations of the different oscillation and different stiffness spring

实验数据分析：

（1）对于振子直径D＝40mm时，并未出现振动现象，可能的原因为机械系统运动阻力比较大，而振子的长径比较小，振子获取旋涡脱落产生的涡激力比较小，未能克服阻力。

（2）同种情况下，仅增大振动系统的弹簧刚度，涡激振动的起振流速增大；

（3）同种情况下，仅增大振动系统的弹簧刚度，涡激振动锁定区间的流速区间数值随之增大。这是因为fn，w正比于弹簧刚度的平方根而锁定区间的折算速度在相对稳定的区间。

6.3 涡激振动耦合模型设计的验证

通过统计实验数据中5种弹簧刚度下不同振子的最大振幅，得到表4，根据表4绘制图10。其中在直径D＝40mm的振子在实验过程中没有出现涡激振动。

实验的流速变化范围：0.4～0.75m/s，涡激振动耦合模型实验设计与振子配合弹簧的刚度值如下：

D＝55mm的振子，弹簧刚度值K＝500、550和600N/m；

D＝70mm的振子，弹簧刚度值K＝350、400和450N/m；

D＝85mm的振子，弹簧刚度值K＝250、300和350N/m；

D＝100mm的振子，弹簧刚度值K＝300、350和400N/m；

通过图9可以看出在选择的弹簧刚度值K范围内，振子的振幅比较大，并且出现振幅的峰值，验证了涡激振动耦合模型设计的合理性。

表4 不同弹簧刚度下达到的最大振幅Table 4 The maximum amplitude under the combinationsof the different oscillation and different stiffness spring

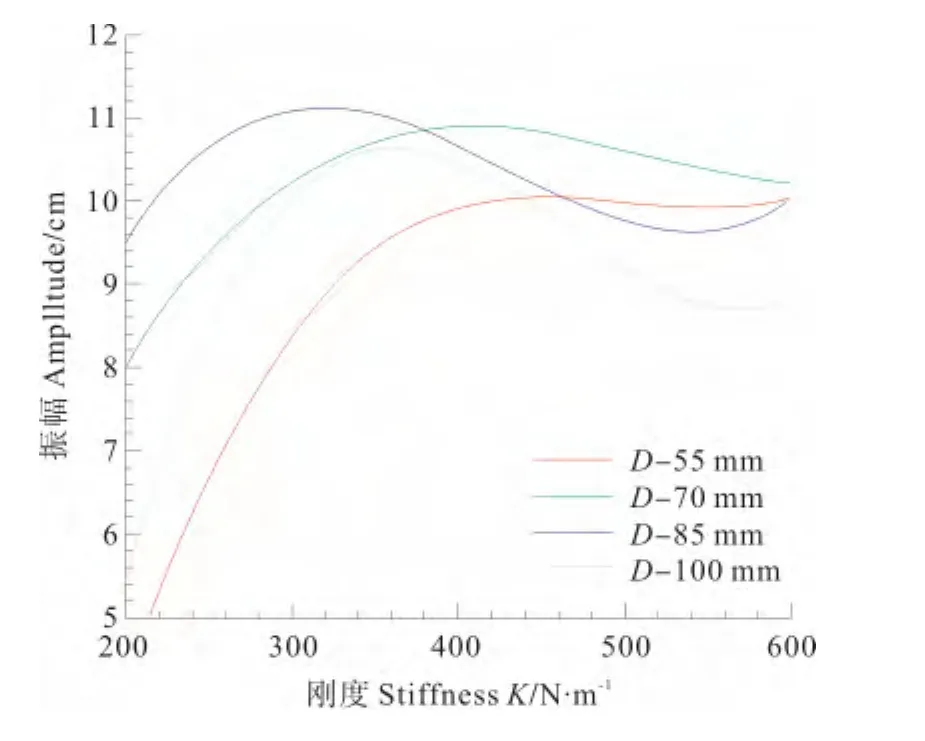
图10 最大振幅走向图Fig.10 The maximum amplitude of the trend graph

7 结语

本文主要对基于涡激振动原理的潮流能转换装置获能原理进行研究，建立了运动方程，将其运动简化为正弦运动，进而对涡激振动的运动方程进行求解，获得涡激振动响应的振动频率和振幅；其次，在求解涡激振动运动方程的基础上，结合经验数据和经验公式，建立涡激振动预测模型，通过与实验结果进行对比，验证了预测模型的合理性；最后，结合理论分析结果和预测模型，确定了涡激振动耦合模型实验样机的关键参数，在后面实验研究，验证了涡激振动耦合模型设计的合理性、正确性。

［1］Shujie Wang，Peng Yuan，Dong Li，et al.An overview of ocean renewable energy in China［J］.Renewable and Sustainable Energy Reviews，2011，15：91-111.

［2］Wang C K，Lu D C.Division of marine resources in coastal rural area of China［C］.Beijing：State Oceanic Administration，Ministry of Resources and Electric Power，1989：25-32.

［3］Wang C K，Lu W.Analysis methods and reserves evaluation of ocean energy resources［C］.Beijing：Ocean Press，2009：54-62.

［4］Bernitsas M M，Raghavan K，Ben-Simon Y，et al.VIVACE（Vortex Induced Vibration Aquatic Clean Energy）：A New Concept in Generation of Clean and Renewable Energy from Fluid Flow［C］.Hamburg：Proceedings of the 25th International Conference on Offshore Mechanics and Arctic Engineering（OMAE′06）［C］.Paper＃92645，2006：112-122.

［5］梁亮文.低雷诺数下圆柱横向受迫振荡和涡激振动的数值分析［D］.上海：上海交通大学，2009.

［6］Che-Chun Chang.Hydrokinetic energy harnessing by enhancement of flow induced motion using passive turbulence control［D］.Michigan：The University of Michigan，2010.