基于三分类支持向量机的多分类算法的研究

翟 嘉，胡毅庆，成小伟

（北京科技大学 天津学院，天津301800）

0 引 言

目前已经有众多学者研究利用支持向量机（SVM）［1］解决多分类问题.最常用的方法是将K类多分类问题转化为一系列二分类问题［2］，包括一对多［3］、一对一［4］、纠错输出编码方法［5］等，最终通过二分类结果的组合得到多分类的结果.随着类别总数K的增加，这些方法的运算量往往增加很快，而分类精度则往往比二分类时差很多.后来有学者提出三分类算法，主要是结合分类机与回归机的思想提出了分类-回归方法，包括K-支持向量分类-回归机（Support Vector Classification-Regression machine for K-class，KSVCR）［6］、ν-K-支 持 向 量分类-回归机（ν-Support Vector Classification-Regression machine for Kclass，ν-K-SVCR）［7］、Total-K-支持 向量分类-回归机（Total Support Vector Classification-Regression machine for K-class，Total K-SVCR）［8］、最小二乘支持向量分类-回归机（Least Square Support Vector Classification-Regression，LSSVCR）［9］，对于求解三分类问题，以上三分类算法表现出了很好的性能.除此之外，为了解决数据点不平衡的情况，最近提出了一种新的机器学习方法：双支持向量机（Twin Support Vector Machine，TSVM）［10-11］，在多分类问题中，结合TSVM与K-SVCR两种算法的优势，有了Twin-KSVC［12］算法，该算法的出现可以更好地解决多分类问题.并且衍生出了v-双支持向量机（ν-Twin Support Vector Machine，ν-TSVM）［13］与最小二乘双支持向量多分类算法（Least Squares Twin Multi-Class Classification Support Vector Machine，LST-KSVC）［14-15］.

由于最小二乘支持向量机在分类过程中会考虑所有的数据点，所以LSSVCR算法对于包含少量错误数据或误差较大的数据也会有很好的分类效果.文中对LSSVCR算法在M空间中从理论上分析了其优越性；并且将三分类算法应用到多分类问题中，提出了一对一对多与一对一对一两种多分类算法；将使用标准测试问题和实际数据集进行数值试验并与已有的基于二分类的多分类算法的分类结果进行比较.

1 三分类算法

给定一个三分类的训练集J=｛（xp，yp）|p=1，2，…k，l｝，其中

对应的三类点集分别称为正类、负类和零类，此时希望建立决策函数f（x），使得f（xp）=yp，p=1，2，…，l.记l12=l1+l2，l3=l-l12，即属于正类与负类的训练点数目为l12，属于零类的训练点数目为l3.

三分类算法的构造思想是将二分类问题中支持向量分类机与回归机结合起来，于是同二分类问题类似，一般来说，考虑的问题是非线性问题，这时，往往引进变换φ∶Rn→F，将数据点映射入更高维的内积空间F中，使其在F中成为线性可分问题再进行求解.但实际计算中并不需要显式地给出映射φ，而是通过相应的核函数k（xi，xj）=（φ（xi）·φ（xj））得到所需的F空间中内积值进行运算.常用的核函数有多项式核函数、高斯径向核函数等.

记该问题的最优解为（ω＊，b＊，ξ＊，φ，φ＊，ρ），则对应分类问题的决策函数为

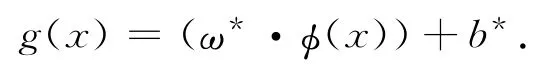
其中，LSSVCR算法描述如下，选取适当的C，D＞0，将最小二乘支持向量分类机与回归机结合在一起，从而得到LSSVCR算法的原始问题

2 LSSVCR算法理论分析

LSSVCR算法是针对三分类问题而提出的，结合最小二乘支持向量分类机与回归机的思想，对正负类样本点作分类的同时对零类样本点作回归而求得的分划平面，下面将对LSSVCR算法作进一步的研究和分析.

2.1 LSSVCR算法分析

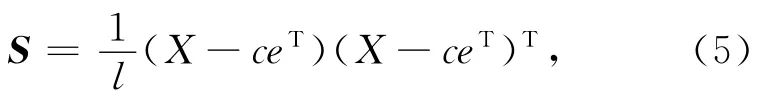
并且，用X1，X2与X3分别表示正类，负类与零类数据集，c1，c2与c3分别为相应的数据集的矩心，从而有

对于任意两个向量u，v，定义其在Mahalanobis距离（简称M距离）下的内积为

其中，S+称为是S的伪逆矩阵，如果S是非奇异的，则S+=S-.则M范数可以定义为

下面进一步分析LSSVCR算法的性质：

因为式（2）等价于

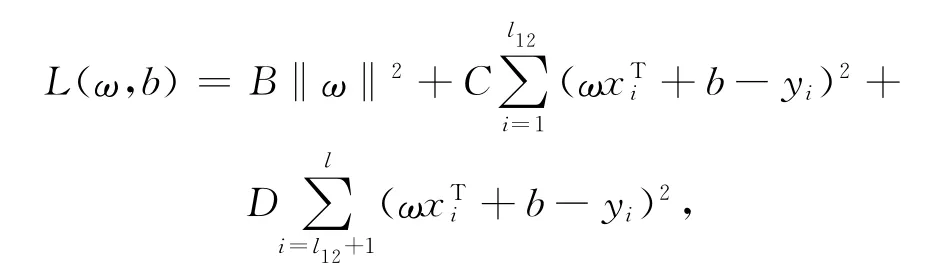
其中，B＞0表示正则化参数.

从而有

由KKT条件，令式（7）为零，可得

令式（6）为零，并且将式（8）代入可得

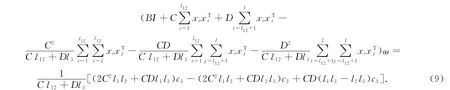
此时，令

则

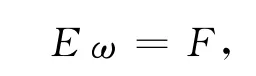
即

考虑以下三种情况：

假设1：C=D

如果假设惩罚因子C=D，将式（5）代入式（10）～（11），那么E与F可以表示为

将式（13）～（14）代入式（12）后可得

假设2：l1=l2

在分类问题中会出现分类样本点中有两类或多类样本点数目相同的情况，考虑这种特殊情况，即假设正类样本点的数目与负类样本点的数目相同时，式（8）与式（15）可化为

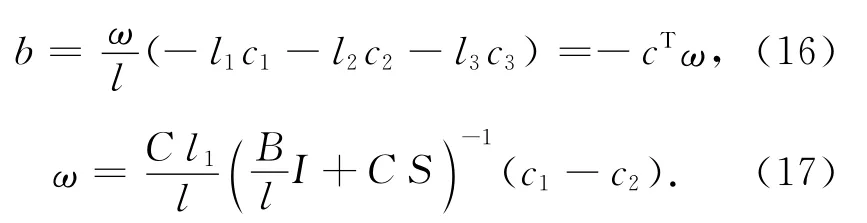
假设3：B=0

考虑无正则化情况，即不对分划平面的法方向ω作限制，只要尽可能分开数据点集即可，此时，式（17）进一步化为

因此，若考虑以上三个条件，则由LSSVCR算法得到的三分类问题的超平面的法方向为S+（c1-c2）.并且如果将该超平面映射到M空间中，那么超平面的法方向为c1-c2，即在M空间中，当正负两类数据点数目相同，那么分划超平面的法方向只取决于正负两类样本点而与零类样本点无关.

2.2 LSSVCR算法推广

Jieping Ye与TaoXiong证明了基于二分类问题的标准支持向量机与最小二乘支持向量机之间的关系，并提出了如下两个定理：

引理1［16］若x∈X1，y∈X2，X1，X2表示两类样本点的集合，且数据集X1，X2为凸包，则其中ai≥0，bi≥0，假 设是线性无关的，对任意的u∈X1，有（u-c1，c1-c2）S=0，对任意的v∈X2，有（v-c2，c1-c2）S=0.

定理1［16］如果c1，c2，X1，X2定义同上，X表示所有样本点的集合，并假设X内的数据点是线性无关的，那么在欧几里德范数下的最小二乘支持向量机等价于在M范数下的硬间隔（C=0）的标准支持向量机.

从Jieping Ye与Tao Xiong的研究中可知，在M空间中，对任意的u∈X1与v∈X2，有c1-c2正交与u-c1与v-c2.并且如果将这些训练集从欧几里德空间映射到M空间中，那么由最小二乘支持向量机得到的分划平面与由SVM算法得到的分划平面是同一个平面.

定理2 如果X表示所有样本点的数据集，c表示X的矩心，假设｛xi｝li=1是线性无关的.在M空间中，当C=D，l1=l2且B=0时，设由LSSVCR算法对三类样本点分类得到的分割超平面为ΩL，那么，X3中的所有零类数据点所在的超平面平行于ΩL.

证明 设正类、负类与零类数据集为X1，X2与X3，且为凸集，相应的矩心分别为c1，c2与c3.令X12=X1∪X2，X13=X1∪X3，X23=X2∪X3，且相应的矩心为c12，c13与c23，那么

在M空间中，对任意xi∈X12，i=1，…，l12，由引理1知

而

因为X1是凸集，则c1∈X12.

则

同理

因为经过c23且垂直于c1-c23的n-1维超平面是存在的，不妨设为Ω23，而对任意xi∈X3，i=l12+1，…，l，有

则

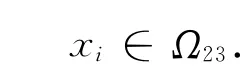
从而

同理，设Ω13经过c13且垂直于c2-c13，那么，X3⊂Ω13.

综上知

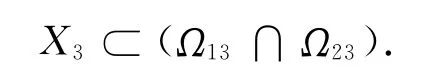
令

则

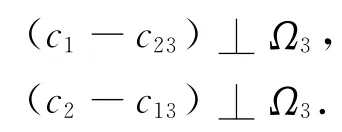
从而有

又因为c3∈Ω3，所以对任意的xi∈X3，有

即

可见，在M空间中所有的零类样本点所在的超平面垂直于c1-c2.而由式（18）知，在欧几里德空间中，由LSSVCR算法对三类数据集分类得到的分类超平面的法方向为S+（c1-c2），所以，如果用M范数度量，该分类超平面的法方向为c1-c2.那么，当C=D，l1=l2且B=0时，由LSSVCR算法对三类数据集分类得到的分类超平面与零类数据点所在的超平面平行.

3 基于三分类支持向量机的多分类算法

在K（K＞3）类多分类问题中，基于三分类支持向量机的多分类算法的思想是将多分类问题看成三分类问题的组合，最终将多分类问题转化成三分类问题.用三分类算法解决多分类问题时最常用的是一对一对多算法（one versus one versus rest，1-v-1-v-r），下面再提出一种多分类算法：一对一对一算法（one versus one versus one，1-v-1-v-1）.

3.1 一对一对多算法

对于K（K＞3）类多分类问题，考虑其中任意两类（θi，θj），把其余的K-2类当成是一类，这样可以将多分类问题转化成三分类问题，并且利用三分类支持向量机可以构造决策函数fi，j（·）把θi，θj，以及其余类别分开.这样共得到K（K-1）／2个决策函数.对于一个新的训练点xp，就可以得到K（K-1）／2个输出，下面判断它所属的类别，采用如下的投票方式：当fi，j（xp）=+1时，xp属于θi类，就在θi类上投上一票，其他两类投0票；当fi，j（xp）=-1时，xp属于θj类，就在θj类上投上一票，其他两类投0票；当fi，j（xp）=0时，xp既不属于θi类也不属于θj类，此时不给任何一类投票.当检验完所有K（K-1）／2个输出后，计算每类的票数.最后xp属于获得票数最多的那一类.

上述分类机能够有效地解决多分类问题，但该算法的一个缺点是所考虑的三分类问题常常是很不对称的，尤其当样本数量很大时，三类问题中会有一类问题的样本数量远远大于其余两类.这种悬殊的差别会引起较大的误差，此时可以利用LSSVCR算法，并且与二分类问题的处理方法类似，可以对不同的类别采用不同的惩罚因子即较少的正负类训练点采用较大的惩罚.为了避免样本点的不平衡，下面的算法也可以较好地解决多分类问题.

3.2 一对一对一算法

对于K（K＞3）类多分类问题，考虑其中的任意三类（θi，θj，θk），然后利用三分类支持向量机可以构造一个决策函数fi，j，k）（·）将这三类样本点分开.这样就可以把K类多分类问题转化成三分类问题的组合.并且可以得到K（K-1）（K-2）／6个决策函数.对于一个新的输入xp，同样采用投票方式来判断xp属于哪一类.当fi，j，k（xp）=+1时，xp属于θi类；当fi，j，k（xp）=-1时，xp属于θj类；当fi，j，k（xp）=0时，xp属于θk类.最后统计票数，xp属于得票数最多的那一类.

在一对一对一算法中不会出现像一对一对多算法中样本数目差异较大的情况（除非原本数据集中每类样本点数目差别较大），即由这个算法得到的每个三分类问题的规模都比较小，所以即使利用该算法得到的三分类问题数目比较多，计算所用时间相当.

基于三分类支持向量机的多分类算法：

1）设已知训练 集：T=｛（x1，y1），…，（xi，yi）｝，其中xi∈Rn，yi∈｛θ1，θ2，…，θk｝，i=1，2，…，l；

2）对于每个三分类支持向量机模型，选择适当的参数及核函数；

3）利用1-v-1-v-r（或1-v-1-v-1）多分类算法，可以构造K（K-1）／2（或K（K-1）（K-2）／6）个决策函数；

4）对于每个输入xp，按照投票规则，输入xp属于得票数最多的一类.

当对大量的数据点做分类时，即K很大时，用上面的多分类算法分类时会产生大量的支持向量机，因为用支持向量机分类的结果往往依赖于少数关键数据点并且对于误差较大的数据点分类结果并不理想，所以可以先用少量的数据点（比如5%的样本点）作为测试点，其余的样本点作为训练点，挑选出分类准确率低于30%的样本点，这个过程相当于是一个校正过程即把分类准确率低的支持向量机去掉，然后用剩余的支持向量机对数据进行分类，这样会提高分类的准确率.

4 试验仿真与分析

试验使用2.2G双核处理器及2G内存的计算机，使用Matlab R2009a编写程序.

数 据 使 用UCI Repository［14］中 的Iris、Hayes-roth、Balance、Seeds、Glass和Ecoil数据集，每个数据集的类别、样本数和特征数见表1.

表1 试验二中使用的数据集 Tab.1 Data sets in experiment 2

在试验中采用Gaussian径向核函数

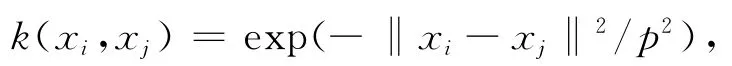
其中，参数p选择见表29.

用Iris、Hayes-roth、Balance、Glass和Ecoil标准数据集做试验时，采用10-折交叉确认的方法统计分类的准确率与分类时间，即从每一类数据中随机选取数据集中10%的数据作为测试样本，其余数据作为训练样本，重复10次试验，最后求10次试验的准确率和时间的平均值作为最终结果.试验过程中先用5%的样本点作为测试点找出分类准确率低于30%的支持向量机，之后从剩余的数据点中选取10%的数据作为测试点并且不考虑挑选出的支持向量机来计算分类的准确率，从数值试验结果表3中可以看出，校正后的分类准确率比校正前平均提高了4.61%.

表2 试验二中的参数值 Tab.2 Parameter values in experiment 2

表3 数值实验结果比较 Tab.3 Comparison of the numerical experiment results

5 结 论

尽管本文提出了基于三分类算法的多分类分类方法以及计算分类准确时使用的技巧，但由于时间以及个人能力方面的限制，从数值试验结果可以看到，三分类算法的分类准确性还有待于进一步提高.同时对于超过三类的多分类算法也还需要更多学者有新的突破，另外还需要做大量的数值实验验证算法的准确性，需要搜集更多的实际数据且数目较大的数据集验证算法的有效性.

［1］邓乃扬，田英杰.支持向量机——理论、算法与拓展［M］.北京：科学出版社，2009.

［2］Cortes C，Vapnik V.Support vector networks［J］.Machine Learning，1995，20（3）：273-297.

［3］Vapnik V.The nature of statistical learning theory［M］.New York：Springer，1995.

［4］Hastie T，Tibshirani R.Classification by pairwise coupling［J］.The Annals of Statistics，1998，26（2）：451-471.

［5］Dietterich T G，Bakiri G.Solving multiclass learning problems via error-correcting output codes［J］.Journal of Artificial Intelligence Research，1995，2（1）：263-286.

［6］Angulo C，Parra X，Catala A.K-SVCR.A Support vector machine for multi-class［J］.Neurocomputing，2003，55（1-2）：57-77.

［7］Zhong P，Fukushima M.A new multi-class support vector algorithm［J］.Optimization Methods and Software，2006，21（3）：359-372.

［8］Xu Y T，Wu C.A total multi-class support vector machine［J］.Journal of Information ffComputational Science，2011，8（7）：1147-1154.

［9］翟嘉，胡毅庆，徐尔.用于多分类问题的最小二乘支持向量分类-回归机［J］.计算机应用，2013，33（7）：1894-1897.Zhai Jia，Hu Yiqing，Xu Er.Least square support vector classification-regression machine for multi-classification problems［J］.Journal of Computer Applications，2013，33（7）：1894-1897.（in Chinese）

［10］Khemchandani R，Chandra S.Twin support vector machines for pattern classification［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2007，29（5）：905-910.

［11］Qi Z J，Tian Y J，Shi Y.Robust twin support vector machine for pattern classification［J］.Pattern Recognition，2012，46（1）：305-316.

［12］Xu Y T，Guo R，Wang L S.A twin multi-class classification support vector machine［J］.Cognitive Computation，2013，5（4）：580-588.

［13］Xu Y T，Guo R.An improved-twin support vector machine［J］.Applied Intelligence，2014，41（1）：42-54.

［14］Kumar A M，Gopal M.Least squares twin support vector machines for pattern classification［J］.Expert Systems with Applications，2008，36（4）：7535-7543.

［15］A.Nasiri J，Charkari M N，Jaloli S.Least squares twin multi-class classification support vector machine［J］.Pattern Recognition，2014，48（1）：984-992.

［16］Ye J P，Xiong T.SVM versus least squares SVM［C］.in the 11th International Conference on Artificial Intelligence and Statistic（AISTATS），2007，640-647.