三维双气泡融合的格子Boltzmann模拟

吕雅琪，聂德明，林建忠

（中国计量学院计量测试工程学院，浙江杭州 310018）

文章编号：1001⁃246X（2015）05⁃0553⁃08

三维双气泡融合的格子Boltzmann模拟

吕雅琪，聂德明∗，林建忠

（中国计量学院计量测试工程学院，浙江杭州 310018）

针对基于自由能模型的格子Boltzmann方法，推导D3Q15格子模型对应的平衡态分布函数；采用该模型模拟双气泡的融合过程.结果表明，气泡的融合不仅与它们之间的初始间距有关，还与表面张力有关.表面张力越大，气泡融合的临界距离也越大.此外，研究气泡融合速度与初始间距、表面张力及粘性系数的关系.

气泡融合；格子Boltzmann方法；表面张力；气液界面

0 引言

气泡运动广泛存在于能源、动力和环境工程设备与工艺中，气泡的运动特性一直以来都是研究的热点.与单气泡相比，多个气泡的运动存在相互作用，如碰撞、融合及破裂等，会出现丰富而复杂的运动现象.此外，由于气泡在运动中可能会变形，因此比一般的颗粒两相流问题更加复杂.

气泡的运动属于典型的带有相界面的气液两相流动.目前已经发展出多种数值方法用于模拟气泡的运动，如Level Set方法［1－3］、VOF（Volume of Fluid）方法［4－6］和格子Boltzmann方法［7－9］等.这些方法在气泡运动的研究中获得了许多成果.格子Boltzmann方法（LBM）是20世纪80年代中期出现的流体计算和物理建模的一种新方法.与传统数值方法不同，LBM并非以连续介质理论为基础，而是基于微观尺度上的统计力学Boltzmann方程.在计算中LBM只涉及一系列的碰撞和流过程步骤，并不需要求解复杂的非线性方程，对于复杂结构的无滑移边界条件很容易实现，且能更加准确合理地描述物理系统的微观动力学机制.因此非常适合涉及界面运动的模拟.近二十几年来已经发展出几种适用于多相流的格子Boltzmann模型，如颜色模型［10］、伪势模型［11］和自由能模型［12］.颜色模型［10］通过颜色梯度来表示不同相之间的界面，而伪势模型［11］则是通过伪势函数来描述不同相之间的相互作用.然而这两种模型在涉及热力学方面计算时遇到很大的限制.自由能模型［12］引入对流扩散方程来描述气液界面，该方程求解简单，易于实现，且可以较好地与其他热模型结合，因此更加适合气泡运动的模拟和研究.

基于自由能模型，Zheng等人［13］提出一种适用于较大气液密度比的格子Boltzmann模型，他们采用双分布函数，分别用来描述流体运动方程和界面运动方程，并针对D2Q9格子模型给出了相应的平衡态的分布函数.通过模拟计算，他们认为双气泡的融合与气泡的初始间距有关，且给出了以下结论，即只有当双气泡初始间距小于两倍界面厚度时，这两个气泡才能融合在一起并形成一个更大的气泡.但这一结论并不全面，首先气泡之间的融合条件应该还涉及其它参数如表面张力和流体粘性等的影响.其次这是基于二维的模拟结果，三维气泡的融合过程可能存在较大差异，需要进一步的研究.另外，从物理机制上来说，气泡的融合现象在多气泡运动的情况中可能会频繁地发生，当气泡相互融合成更大的气泡时，会显著影响气泡群的运动特性，进而影响到气泡群的运动速度以及平均阻力系数等［15］，因此值得深入的研究.然而，以往对于气泡融合条件的研究较缺乏，尤其在三维方面更缺乏系统的研究成果.本文采用Zheng等人［13－14］提出的基于自由能模型的格子Boltzmann方法，推导D3Q15格子模型对应的平衡态分布函数，并对双气泡的融合条件进行模拟研究，考虑表面张力、粘性系数以及气泡间距的影响.此外，论文还对气泡的融合速度进行细致地研究.

1 数值方法

流体运动的Navier⁃Stokes方程和界面演化方程为

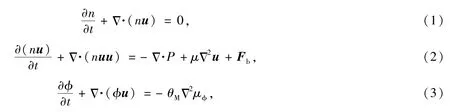
式中θM是迁移率，P是压力，Fb是体积力，n是半密度和，ϕ是半密度差（也叫相序参数），即n＝（ρA＋ρB）/2，ϕ＝（ρA－ρB）/2.ρA和ρB是流体A和流体B的密度.μϕ是化学势能，根据Zheng等人［13］，μϕ可以表示为

其中，ϕ∗是与平衡状态相关的常数，即

ρH和ρL分别代表两相中的高密度和低密度.系数A定义为，

式中σ为表面张力，W为界面厚度.κ的表达式为

1.1 连续方程和动量方程的求解

根据Zheng等人［13］，连续性方程（1）和动量方程（2）采用带有外力项的格子Boltzmann演化方程求解，即

为了模拟三维的气泡运动，本文采用D3Q15格子模型，其离散速度方向为

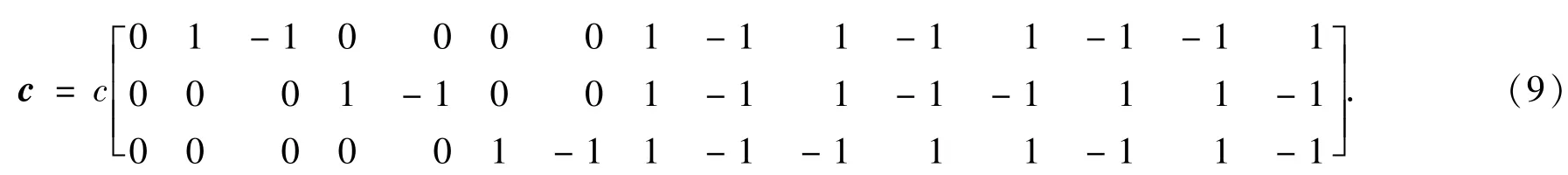
采用如下所示的平衡态分布函数，

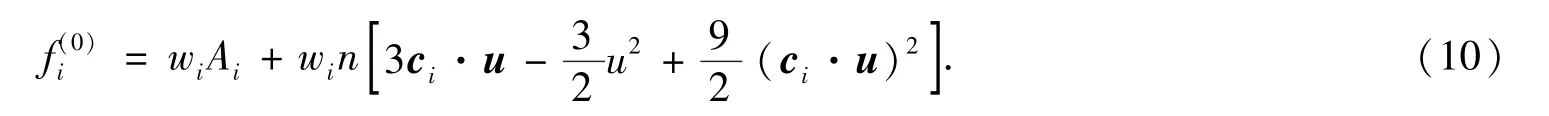
为了得到式中的系数Ai和权系wi，引入质量、动量和二阶速度矩的守恒关系，即，

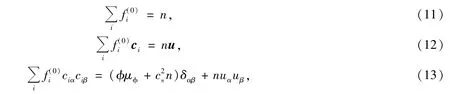
其中格子速度cs＝c2/3，将平衡态分布函数 （10）代入式（11）、（12）及（13），考虑D3Q15的格子速度矢量（9），可以得到对应的系数Ai和权系数wi，

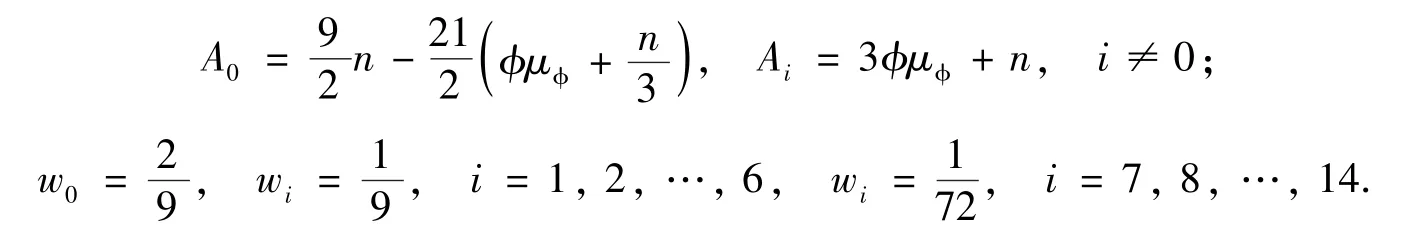
1.2 界面捕捉方程的求解

为了求解界面方程（3），采用如下形式的格子Boltzmann演化方程［13］，

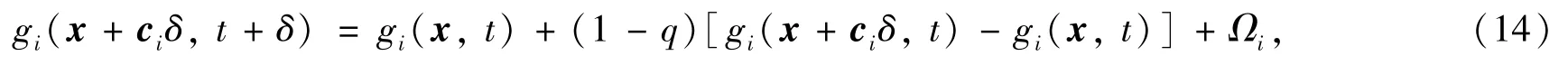
式中，碰撞项为Ωi＝［g（i0）（x，t）－gi（x，t）］/τϕ，tϕ为无量纲松弛时间，q与tϕ有关即q＝1/（τϕ＋0.5）．

根据Zheng等人［14］，gi的平衡态分布函数为

采用D3Q7模型，其离散的速度方向为，

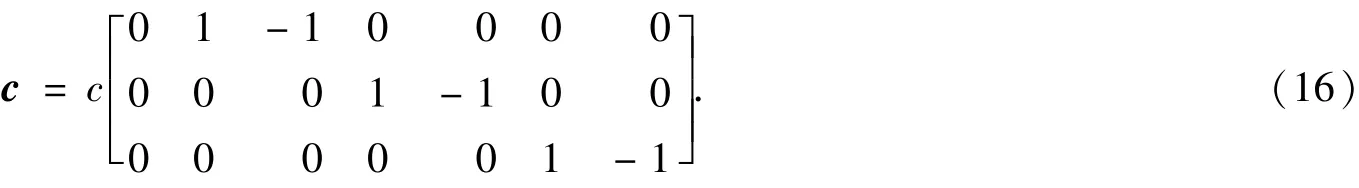
为了得到式中的系数Ai、Bi和Ci，引入质量、动量和二阶速度矩的守恒关系，即，

则可以推得各项系数

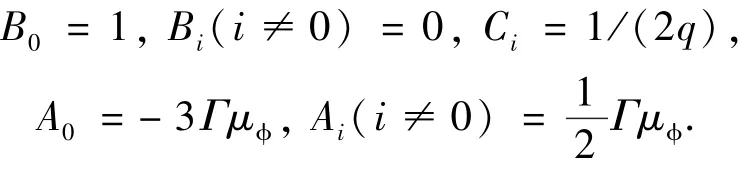
其中Γ与迁移系数相关.

1.3 模型验证

根据Jacqmin［16］，关于球形气泡的相序参数即气液界面的理论值为，

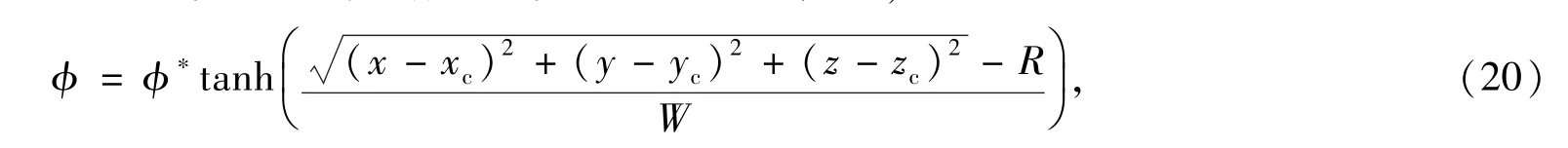
其中xc、yc和zc是气泡中心的坐标.上式可以用来表示气液的界面曲线.为了验证本文的方法，采用式（20）进行验证.

设置计算区域为N3＝64×64×64，表面张力σ＝1.0，界面宽度W＝3.5.对以下两种情况进行模拟：①气泡半径R＝10，ρH＝1 000，ρL＝1；②气泡半径R＝15，ρH＝500，ρL＝1.结果如图1所示，符号表示的是本文D3Q15对应的数值解，实线和虚线对应的是理论解即式（20）.可以看到，本文采用的方法准确地捕捉到了气液的界面曲线.

Zheng等人［13］研究表明，界面厚度W对模拟的结果有影响，具体而言，对于半径为R的气泡，当选取的W较小时会出现比较明显的误差.为此，我们设置 R＝20，ρH＝1 000，ρL＝1以及σ＝1.0，分别选取W＝1.5，2.0，2.5，3.5 和4.5，通过计算可以得到气泡内外的压力差Δp.对于球形气泡，通过内外压力差和表面张力的平衡方程可以得到Δp ＝2σ/R（二维的表达式为Δp＝σ/R）.根据这一表达式可以计算表面张力，显然这个结果与设置的值有差别，通过这个差别可以评估相应的误差.结果如图2所示，可以看到，随着界面厚度W的增大，计算所得的表面张力逐渐靠近理论值即σ＝1，当W＝4.5时，计算值与理论值的误差小于5％，因此在后续的计算中界面厚度均采用W＝4.5.

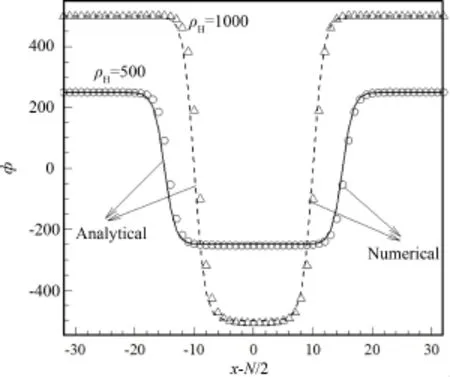
图1 气液界面的数值解与理论解Fig.1 Analytical solution and numerical results for gas⁃liquid interface profile

另外，Huang等人［14］曾建立基于D3Q19的格子Boltzmann方法并用来模拟气液两相流动.与D3Q19速度离散模型相比，本文基于D3Q15的方法在每个节点节省了4个方向的存储数据.对于三维计算而言，网格量大，因此既可以节省内存，同时也提高计算效率.为了说明这一点，设置以下两个算例：①计算区域N3＝60×60×60，气泡半径R＝10，表面张力σ＝0.5，初始气泡间距d＝0.5W；②计算区域N3＝120×120×120，气泡半径R＝20，表面张力σ＝1.0，初始气泡间距d＝0.1W.为了得到气泡的运动的速度，需要采用统计平均的方法进行计算，

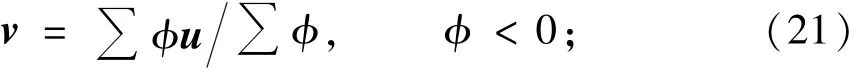
式中ϕ＜0代表的是气相区域.由于两个气泡在流场中是水平对称的，因此根据（21）得到的气泡平均速度始终为零.为了更加细致地研究气泡的融合过程，仅对计算区域的左半部分的流场进行统计，这样得到的是左边的气泡在运动和融合过程中的速度.结果如图3所示，从图中可以看出，采用D3Q15和D3Q19速度离散模型计算出的气泡融合速度曲线几乎重合，说明两个模型的计算结果是一致的.更进一步地，表1给出了二者对应的计算时间，当计算区域为N3＝60×60×60，达到20 200迭代步时，D3Q15模型比D3Q19模型所用的时间减少了约18％；当计算区域为N3＝120×120×120，达到22 500迭代步时，D3Q15速度离散模型比D3Q19速度离散模型所用的时间减少了约16％.因此，本文采用的D3Q15模型能较显著地节省计算资源和提高运算效率.

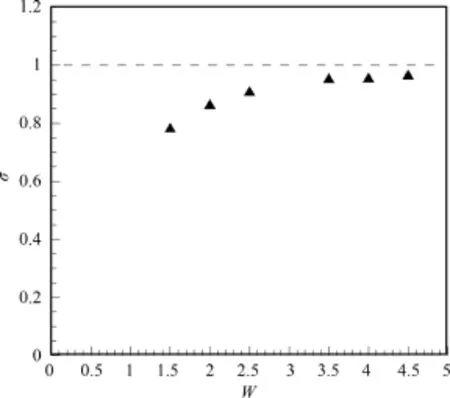
图2 通过界面厚度W计算得到的表面张力σFig.2 Surface tension computed at different thickness of interface layer

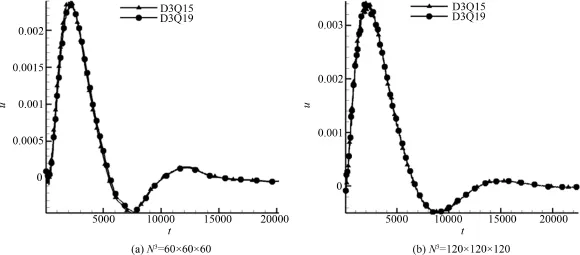
图3 D3Q15和D3Q19格子模型的气泡融合速度Fig.3Merging velocity in D3Q15 and D3Q19

2 结果及讨论

首先研究气泡初始间距对气泡融合的影响.计算区域设置为N3＝120×120×120，采用周期性边界条件，初始时刻流场处于静止状态.参数设置为气泡半径R＝20，无量纲时间因子τn＝0.6和τϕ＝0.7，ρH＝1 000，ρL＝1，表面张力σ＝0.5，Γ＝800以及界面厚度W＝4.5.

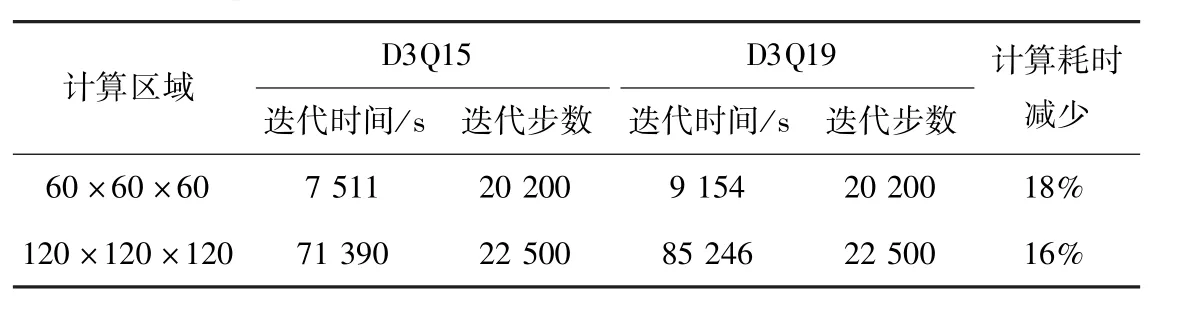
表1 D3Q15和D3Q19速度离散模型效率Table 1 Com putational efficiency in D3Q15 and D3Q19 velocity model

图4给出气泡初始间距d＝2.0W时双气泡融合的过程.当两气泡开始接触时气泡的界面发生形变，在表面张力的作用下，两气泡有融合成一个气泡的趋势，如图4（a）和（b）所示.气泡呈横向椭球形时气泡的变形最大，如图4（c）所示，此时在表面张力作用下气泡有恢复成球形的趋势，如图4（d）所示.当气泡恢复成球形后，在惯性的作用下，气泡继续朝向中心运动.此时圆形逐渐变成纵向椭球形，如图4（e）所示.经过几次振荡变形，伴随着粘性的耗散，气泡最终变成稳定的球形，如图4（f）所示.

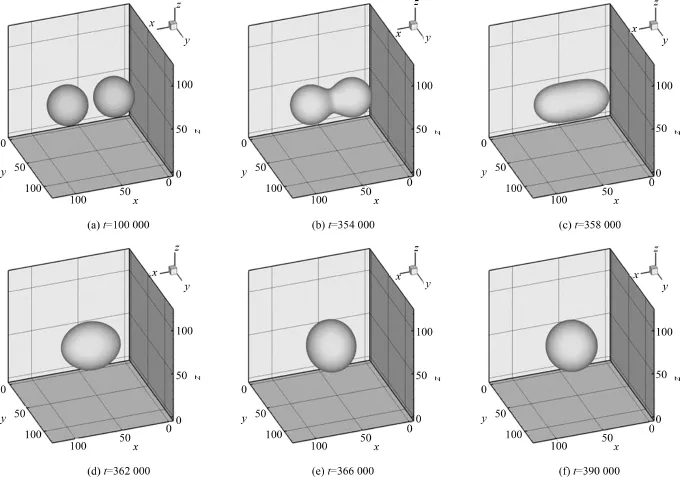
图4 两个气泡的融合过程（d＝2.0W）Fig.4 Merging process shown by contours of order parameter at different times（d＝2.0W）

若增大气泡的初始间距如d＝2.5W，则发现在计算中即使经历很长时间两个气泡也没有相互靠近的趋势，一直保持静止不动，不发生融合，如图5所示.显然，气泡的初始间距是气泡融合的关键参数之一.

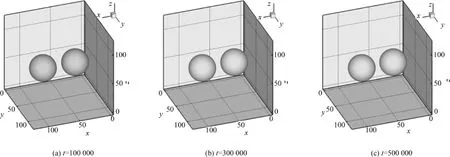
图5 两个气泡相序参数随时间演化（d＝2.5W）Fig.5 Merging process shown by contours of order parameter at different times（d＝2.5W）

通过计算发现，气泡的融合不仅与初始间距的大小有关，还与表面张力有关.为了研究这二者对气泡的影响，选取三组表面张力即σ＝0.5，1.0和1.5，在不同间距d下进行模拟，观察气泡是否能靠近并融合在一起.统计这些结果可以得到如图6所示的图形，可以看到，表面张力越大，气泡能融合的最大间距及临界间距dc越大.例如，当表面张力σ＝0.5时，两个气泡能融合在一起的临界间距为dc＝2.0W，而当σ＝1.0时，临界间距为dc＝2.5W.显然，这与Zheng等人［13］在二维情况下研究的结果不一致.说明圆形气泡间的相互作用与球形气泡之间的相互作用并不等同.特别地，当表面张力σ＝1.5时，即使在气泡间距为4W时还能观察到融合的现象，说明表面张力对气泡融合的影响非常显著.究其原因，表面张力σ越大，化学势能越大，因此气泡融合的驱动力越大.

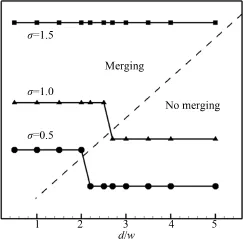
图6 气泡融合与间距和表面张力的关系Fig.6 Bubblemerging dependence on surface tension and bubble distance

图7给出不同表面张力对应的气泡融合速度曲线.可以看到，融合过程的速度曲线相似，即经历一正一负的峰值之后迅速衰减为零.对于同一表面张力，不同的初始间距对气泡的融合速度有一定的影响，如图所示，当气泡间距小于1.5W时，速度峰值明显更大，而当间距大于1.5W时，可以看到，所有的速度曲线的几乎一样.此外，间距越小气泡应该越早融合，这一点从图7（a）和（b）可以得到证实，但比较特殊的是，当表面张力σ＝1.5时，发现d＝5W较之d＝2.5W，3.5W和4W更早融合，这与计算中设置的周期性边界条件有关.图8给出了相同间距的情况下不同表面张力对气泡融合速度的影响，可以看到，表面张力越大，气泡开始融合的时间越早，而且气泡融合的速度峰值也越大.

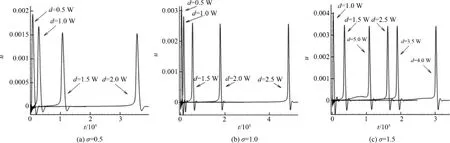
图7 不同初始间距对应的气泡融合速度Fig.7 Merging velocity at different initial bubble distances

下面研究流体粘性系数对气泡融合过程的影响，固定气泡初始间距 d＝1.5W，分别取无量纲时间因子τn＝0.55，0.57和0.60，则粘性系数ν分别为1/60，1.4/60 和1/30，对应的气泡融合速度曲线如图9所示.可以看到，粘性系数越小气泡融合速度的峰值越大，且速度曲线的振荡越明显.ν＝1/60时出现了5个速度峰值，ν＝1.4/60时出现了4个速度峰值，而ν＝1/30时只出现了3个速度峰值.这说明气泡融合所具有的化学势能是通过粘性进行耗散的，所以粘性越大，耗散越快.更进一步，图10给出了两个气泡融合成一个气泡的过程中，气泡呈纵向椭球形时变形最大的形态.可以看到，随着粘性系数的增加，气泡最大变形越来越小.这是因为粘性系数体现了流体对气泡运动阻碍的强烈程度.粘性系数大，气泡受到的阻力大，运动过程中的粘性耗散也大.所以粘性系数越大，气泡融合的速度峰值越小，气泡形变越小.

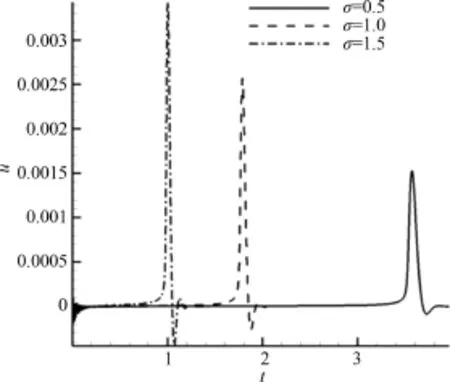
图8 不同表面张力对应的气泡融合速度（d＝2.0W）Fig.8 Merging velocity with different surface tension coefficients（d＝2.0W）

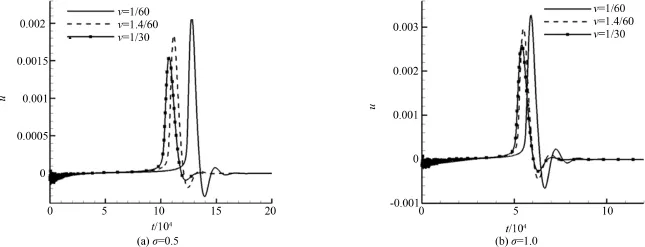
图9 不同粘性系数对应的气泡融合速度Fig.9 Merging velocity with different viscosities

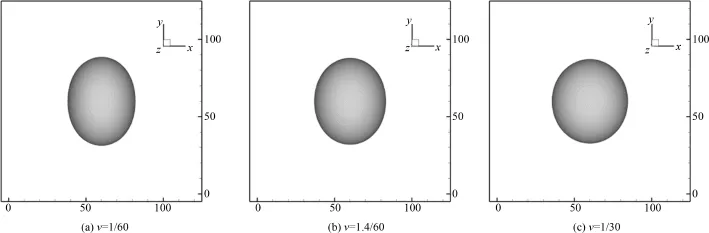
图10 不同粘性系数下气泡纵向最大变形形态Fig.10 Contours of order parameter for bubble ofmaximum vertical deformation with different viscosities

从图9和图10可以看到，流体的粘性显然对气泡的融合过程具有影响，但应该与气泡是否融合无关.为了说明这一点同时为了节省计算时间，我们设置计算区域为N3＝60×60×60，气泡半径R＝10，ρH＝1 000，ρL＝1，表面张力σ＝0.5以及界面厚度W＝2.25，分别取τn＝0.55，0.57和0.60.考察不同粘性下气泡的融合过程.通过计算发现，对于上述三种情况，当气泡间距小于两倍界面厚度时都发现气泡融合现象，否则都不会融合.由此可见，粘性的大小不影响气泡是否融合.

3 结论

采用基于自由能模型的Boltzmann方法，模拟了三维情况下双气泡的融合.首先针对D3Q15格子模型推导了对应的平衡态分布函数，并通过气液界面的理论解进行了验证.计算结果表明，气泡的融合不仅与气泡之间的初始间距有关，还与表面张力有关，结论如下：

1）与D3Q19速度离散模型相比，D3Q15速度离散模型在每个节点节省了4个方向的存储数据，且所用的计算时间减少15％以上.因此D3Q15速度离散模型能较显著地节省计算资源和提高运算效率.

2）表面张力越大，双气泡融合成一个气泡的临界间距越大.特别地，当表面张力σ＝1.5时，即使间距d＝4.0W时也能观察到气泡的融合，这与二维的结论不一致.另外，表面张力越大，气泡融合的时间越早，融合的速度也越快.

3）气泡初始间距越小，气泡融合的时间越早.而且，当气泡间距d＜1.5W时，间距越小气泡融合速度的峰值越大，而当气泡间距d＞1.5W时，气泡间距对融合速度的峰值几乎没有影响.

4）流体黏性系数对气泡能否融合不起关键作用，但流体黏性会影响气泡的融合过程.流体粘性系数越小，气泡融合的速度峰值越大，气泡变形越大，融合速度曲线的振荡越明显，从定量的角度描述了粘性耗散的过程.

［1］ 李彦鹏，张乾隆，白博峰.竖直通道内相邻气泡对上升的直接数值模拟［J］.热能动力工程，2007，22（4）：375－379.

［2］ 陈菲，张梦萍，徐胜利.运动激波和气泡串相互作用的初步数值模拟［J］.计算物理，2004，21（5）：443－448.

［3］ Sussman M，Fatemi E，Smereka P，Osher S.An improved level setmethod for incompressible two⁃phase flows［J］.Comput Fluids，1998，27：663－680.

［4］ Pilliod JE，Puckett EG.Second⁃order volume⁃of⁃fluid algorithms for trackingmaterial interfaces［J］.JComput Phys，2004，199：465－502.

［5］ 李维仲，赵大勇，陈贵军.竖直流道宽度对气泡运动行为影响的数值模拟［J］.计算力学学报，2006，23（2）：196－201.

［6］ 张淑君，吴锤结.气泡之间相互作用的数值模拟［J］.水动力学研究与进展A辑，2008，23（6）：681－686.

［7］ 孙涛，李维仲，杨柏丞，祝普庆.气泡群上升过程相互作用的格子Boltzmann三维数值模拟［J］.化工学报，2013，（5）：1586－1591.

［8］ 曾建邦，李隆键，蒋方明.气泡成核过程的格子Boltzmann方法模拟［J］.物理学报，2013，62（17）：176401.

［9］ Cheng M，Hua J，Lou J.Simulation of bubble⁃bubble interaction using a lattice Boltzmann method［J］.Comput Fluids，2010，39：260－270.

［10］ Gunstensen A K，Rothman D H，ZaleskiS，ZanettiG.Lattice Boltzmannmodel of immiscible fluids［J］.Phys Rev A，1991，43：4320－4327.

［11］ Shan X，Chen H.Lattice Boltzmannmodel for simulating flowswithmultiple phases and components［J］.Phys Rev E，1993，47（3）：2557－2562.

［12］ SwiftM R，OsborneW，Yeomans JM.Lattice Boltzmann simulation of nonideal fluids［J］.Phys Rev Lett，1995，75：830－833.

［13］ Zheng H W，Shu C，Chew Y T.A lattice Boltzmann model formultiphase flows with large density ratio［J］.JComput Phys，2006，218：353－371.

［14］ Huang H B，Zheng H W，Lu X Y，Shu C.An evaluation of a 3D free⁃energy⁃based lattice Boltzmann model for multiphase flowswith large density ratio［J］.Int JNumer Meth Fluids，2010，63：1193－1207.

［15］ Gupta A，Kumar R.Lattice Boltzmann simulation to studymultiple bubble dynamics［J］.Int JHeat Mass Trans，2008，51：5192－5203.

［16］ Jacqmin D.Calculation of two⁃phase Navier⁃Stokes flows using phase⁃fieldmodeling［J］.JComput Phys，1999，155：96－127.

Lattice Boltzmann Simulation of Gas Bubble M erging in Three Dimensions

LV Yaqi，NIE Deming，LIN Jianzhong
（College ofMetrology and Technology Engineering，China Jiliang University，Hangzhou 310018，China）

Equilibrium distribution functions for latticemodel D3Q15 are proposed in the framework of lattice Boltzmann method in free energymodel.Bubblemerging process is studied.It shows that bubblemerging not only depends on initial bubble distance，but also depends on surface tension.The greater the surface tension is，the greater the critical distance for bubblemerging.Furthermore，influence of initial bubble distance，surface tension and viscosity onmerging velocity are investigated.

bubblemerging；lattice Boltzmann method；surface tension；gas⁃liquid interface

O359

A

2014－09－26；

2014－12－21

国家重点基础研究发展计划（2011CB706501）及国家自然科学基金（11272302）资助项目

吕雅琪（1991－），女，硕士生，主要从事气液两相流的研究，E⁃mail：lv_yaqi＠126.com

∗通讯作者：E⁃mail：nieinhz＠cjlu.edu.cn

Received date： 2014－09－26；Revised date： 2014－12－21