基于VOSET方法模拟并排气泡的上升过程

李隆键，张 磊，朱文冰，申宪文

（重庆大学动力工程学院，重庆 400030）

文章编号：1001⁃246X（2015）05⁃0545⁃08

基于VOSET方法模拟并排气泡的上升过程

李隆键，张 磊，朱文冰，申宪文

（重庆大学动力工程学院，重庆 400030）

采用VOSET方法和耦合表面张力模型的N⁃S方程，模拟竖直通道内并排气泡对的上升过程，模拟与实验结果吻合较好.重点研究表面张力系数对并排气泡上升轨迹和速度的影响.结果表明，随着表面张力系数的变化，并排气泡对的上升过程出现三种类型：两气泡融合，两气泡反复靠近、远离但未融合，两气泡碰撞反弹后逐渐远离.在未融合的情况下，并排气泡对的上升轨迹关于通道中心线对称，左右两个气泡的上升速度基本一致，水平速度大小相同，方向相反.

并排气泡；数值模拟；VOSET

0 引言

多相流广泛存在于能源、动力和环境等工程设备和工艺中，如核电站的蒸汽发生器、火箭发动机、鼓泡反应器等工业设备.这些过程往往涉及到多个气泡的融合、破碎等复杂变化.气泡之间的相互作用显著影响气泡的形状和运动特性，因此，准确研究气泡之间的相互作用，如各个气泡速度的波动，气泡的融合和反弹等，对研究多相流尤其是泡状流的运动特性具有重要意义.

Sanada等［1］实验研究了静止流体中一对轻微变形的并排气泡的反弹和融合特性，使用高速照相机对气泡的运动轨迹和尾迹进行了可视化研究.Duineveld等［2］实验研究了高Re数下气泡对在纯水中和含有活性剂的水中的相互作用，分析了Weber数对气泡对运动的影响.

随着数值模拟技术的发展，越来越多的学者采用数值方法来研究气泡间的运动行为.张淑君等［3］采用结合PLIC界面重构的VOF方法，模拟了不同放置方式下气泡之间的相互作用，重点研究了周围流体黏性及气泡间距对气泡融合的影响.赵知辛等［4］采用Level Set方法对水下两个直径为8mm的气泡的运动过程进行数值模拟.Chen等人［5］使用MPS方法（移动粒子半隐式法）对静止液体中气泡对的上升进行了数值模拟，研究了水平并排气泡对和竖直同轴两个气泡的融合过程.王太等［6］采用三维的VOF方法模拟研究了竖直同轴两个气泡的融合过程，分析了液体粘度和表面张力对同轴气泡融合的影响.

直径为2mm左右的气泡广泛存在于泡状流动等实际过程中［2］，Wu等［7］实验研究了直径为1mm～2mm的气泡在水中上升的形状和路径，实验发现直径小于1.5mm的气泡呈直线上升，更大的球形气泡则呈“之”字形或螺旋状上升.Sone等［8］实验研究了静止流体中一对“之”字形气泡碰撞过程中气泡和周围流体的运动.在以往的模拟中，主要研究的是较大气泡间的相互作用，而小气泡间的相互作用研究较少.本文采用数值模拟方法，研究小气泡的相互作用过程，该范围内气泡的Re数较大，且呈“之”字形上升.

气泡的融合过程涉及到复杂的相界面变化，对数值方法的要求较高.VOF方法缺点是难以计算曲率及处理界面附近突变的物理量，Level Set方法不能保证质量守恒，这两种方法都有一定的局限性.结合二者方法的优点，Sun［9］等人提出VOSET方法，该方法被证明能够模拟复杂的界面拓扑变化，且能保证质量守恒.Sun分别通过三个二维的不相溶，不可压的两相问题对VOF，Level Set和VOSET方法进行计算分析，VOSET的界面曲率、精度、整场的密度和粘度的光顺性，质量守恒特性均优于其它两种方法.叶政钦［10］采用VOSET方法针对两个同轴气泡及多个气泡的上升和融合过程进行了模拟，分析了复杂两相流动问题中VOSET方法的质量守恒特性、几何计算方法的可靠性及求解过程的稳定性.

采用VOSET方法，结合考虑表面张力的气液运动基本方程，数值模拟水平并排放置的一对半径R＝0.9mm气泡对在竖直通道内的上升过程，研究气泡对相互作用规律.

1 数学模型

1.1 控制方程

对粘性不可压缩两相流动，其控制方程为

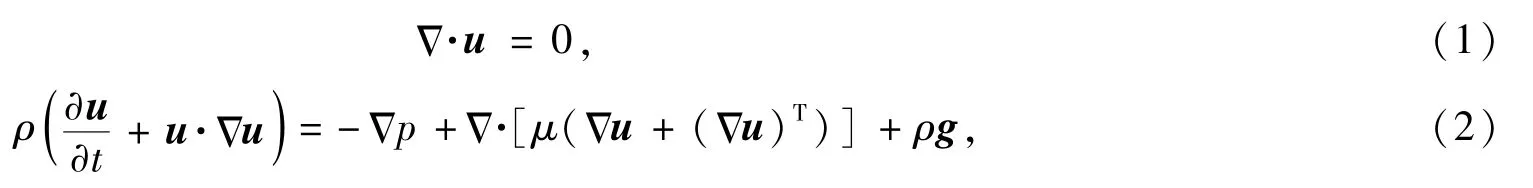
式中，g为重力加速度，u为速度矢量，ρ为流体密度，μ为流体的粘性.

在界面附近，考虑表面张力的作用，对动量方程进行修正，采用CSF模型［11］（连续表面张力模型），将界面上的表面力转化为相应的控制容积中的体积力.利用Level Set函数［12］ϕ对动量方程进行修正，修正后的动量方程

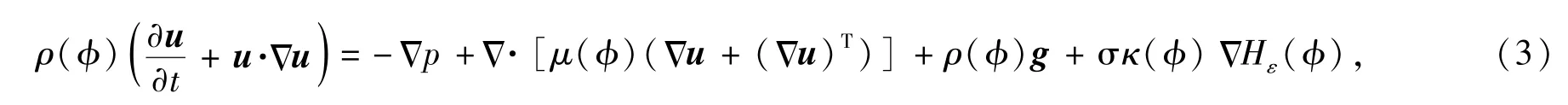
式中，σ为表面张力系数，κ（ϕ）为曲率，

Hε（ϕ）为光滑的Heaviside函数，定义为

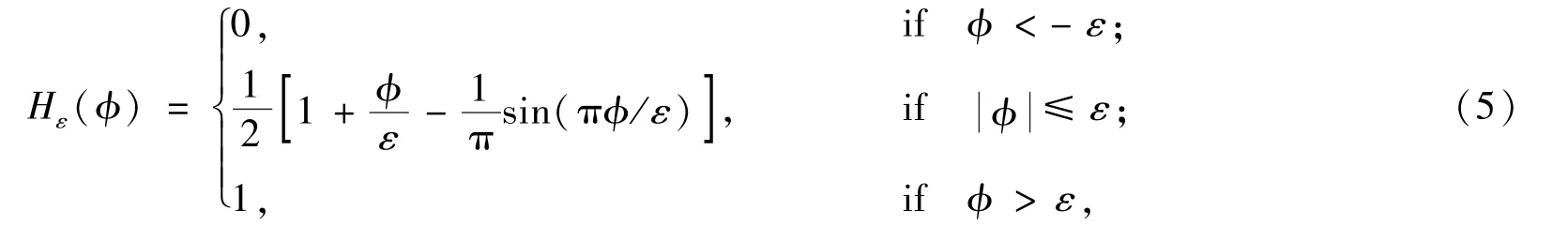
其中ε表示界面处光滑区间单侧的宽度，一般ε＝1.5Δ，Δ表示最小的网格的宽度.

为了使物性在界面上连续光滑变化，流体物性可借助于Heaviside函数做插值计算.这样整场的密度和动力粘度可表示为

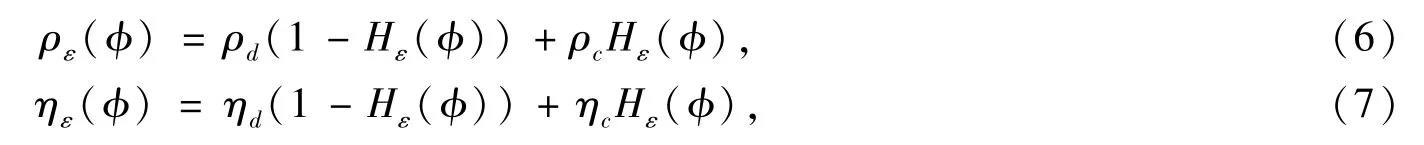
在界面追踪方法中，VOF方法和Level Set方法是目前运动界面问题中应用较为广泛的数值方法.VOF方法中引入了流体体积函数C的概念，对于两相流动流体分为目标流体和非目标流体，流体体积函数C等于一个单元内目标流体与该单元体积之比.对于不可压缩流动，流体体积函数C的输运方程为

Level Set方法［12］的主要思想是把随时间运动的物质界面看作某个函数ϕ（x，t）的零等值面.在每个时刻t，我们只要求出函数的值，求出其零等值面的位置，也就能得到运动界面的位置.首先需构造函数ϕ（x，t），使得在任意时刻t运动界面Γ（t）恰是ϕ（x，t）的零等值面．一般可取ϕ（x，t）为x点到界面Γ（0）的符号距离.

Γ（t）表示t时刻的自由界面，其中d（x，Γ（t））表示区域中任一点到Γ（t）的距离．在任意时刻t，对于活动界面Γ（t）上的任意点x，ϕ（x，t）＝0，即符号距离函数的零等值面即为自由界面.

VOSET方法的主要思想是：流体体积函数C的输运仍然采用VOF中C的输运方程，并结合PLIC界面重构方法来更新下一时刻的流体体积函数C.PLIC界面重构方法的思路是：首先在单个网格内用直线段来重构界面，逼近真实界面，然后计算流过该网格各边界的目标流体的体积流量，从而计算出下一时刻的流体体积函数.

与一般的VOF方法中直接采用C来加权计算界面附近的参数不同的是，VOSET方法在每个时刻通过已知的流体体积函数C，采用几何迭代方法计算单元（i，j）距其计算范围内网格上所有界面的最小距离后，通过比较可以得出单元（i，j）距离界面的最短距离d，然后通过式（9）计算符号距离函数ϕ，利用此ϕ函数求得界面附近的曲率和物性参数，具体实施方法参见文献［9］.

1.2 计算区域和边界条件的选择

为了满足计算区域的要求和节省计算资源，根据文献［5］的结论，当气泡中心和壁面的距离大于5倍半径时，壁面的影响可以忽略不计，而且高度要足够大使气泡能够达到终端速度和终端形状.综合考虑，本文选择12mm×24mm的矩形区域，各边界条件采用无滑移边界条件.

1.3 计算流程

本文采用有限体积法对流场进行离散求解，利用VOSET方法捕捉界面.求解步骤为：①对流场进行初始化，给出初始的流体体积函数C的分布；②利用C的分布求得符号距离函数ϕ的分布，按照式（4）～（7）计算相关的参数，使用IDEAL［13］数值算法求解控制式（1）～（3），获得收敛的速度场；③采用VOSET方法求得下一时刻流体体积函数C的分布；④返回步骤①，进入下一时间步的计算.

2 结果与分析

2.1 模型的验证

首先对静止液体中单个气泡的上升过程进行数值模拟，以验证模型的正确性.计算区域为12mm×24mm的矩形区域，区域内充满静止液体.液体的物性参数：ρl＝1 000 kg·m－3，μl＝0.001 Pa·s；气体的物性参数：ρg＝1.1 kg·m－3，μg＝1.8×10－5Pa·s，表面张力系数σ0＝0.072 8 N·m－1，E o＝0.5，M o＝2.5× 10－11.直径d＝0.001 88 m的气泡从（0.006 m，0.002 m）的位置释放.经网格无关性验证，网格数取90× 180，计算得到的单个气泡上升过程如图1所示，气泡由初始的球形连续变化为扁椭球状，与Fan［14］给出的气泡形状图谱吻合.该气泡的最终上升的速度为22.4 cm·s－1，与文献［7］中20 cm·s－1的速度很接近，证明了该模型的正确性.

图1 单个气泡上升模拟Fig.1 Simulation of single bubble rising in quiescent liquid

2.2 水平气泡对的上升

一个12mm×24mm大小的竖直通道，距底部3mm处，两个直径为1.8mm的球形气泡关于通道中心线对称并排放置，气液物性和上述的一致.两气泡中心的初始水平距离为2.2mm，内边缘相距0.4mm.随着气泡的上升，两个气泡相互靠近，之后接触、融合，变成一个更大的气泡继续上升.融合后的气泡没有稳定的形状，在上升的过程中伴随着形状的震荡，模拟结果如图2所示，数值模拟的结果与Duineveld［2］的实验结果吻合较好（图3）.其实验条件：10cm×10cm×50 cm立方玻璃水箱，水温20℃，玻璃箱下面有两个相距一定距离的注射器，磁力阀推动注射器里面的柱塞运动，从而产生气泡.实验中采用一系列的措施基本保证两个气泡能够同时释放，而且初始为球状且没有形状的波动，利用高速摄像机拍出气泡运动图.类似的气泡融合过程也能在Sanada的实验［1］中观察到.

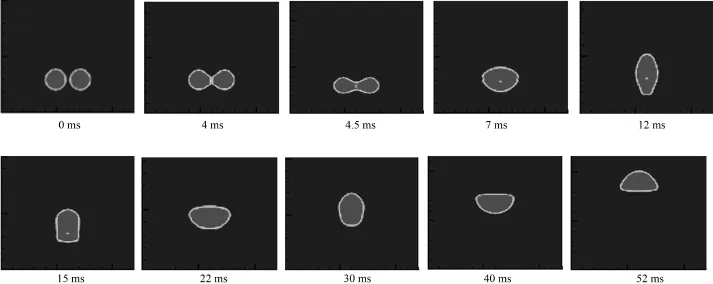
图2 并排气泡融合数值模拟Fig.2 Simulation of side by side coalescence between two identical bubbles

图3 Duineveld（1998）实验结果Fig.3 Experimental observations of side by side coalescence between two identical bubbles

在两气泡靠近融合的过程中，两气泡融合前对称上升，上升速度基本相同.气泡上升的速度随时间变化如图4（a）所示.两气泡在融合前的上升过程中，中间会形成一个低压区，从而两个气泡会相互靠近，如图4 （b）所示.可以看出在接触之前的上升过程中，两气泡对称上升，速度逐渐增大.接触时，当两个气泡开始融合到接触面积达到最大时，其体积大大增加，在上升方向产生的阻力达到最大，因此气泡上升速度呈现下降趋势.而当融合后的形状开始收缩时，气泡上升速度亦开始反弹上升，最后呈波动增大.气泡在融合过程中上升速度出现了上升－下降－上升的波动现象，这个结果与Sanada［1］实验的结果相吻合.融合后的气泡形状波动变化，导致受力不均匀，从而导致速度的波动.这与张淑君等［3］对低Re数下的气泡对融合上升最终会有一个稳定的形状和上升速度不同.这是因为高Re数下，气泡尾迹的作用使得气泡没有稳定的形状.赵知辛［4］模拟水中相同相对中心距下8mm的气泡，两气泡没有发生融合，可见小气泡更易融合.

2.3 表面张力对气泡融合的影响

气液界面的表面张力系数是重要的物性参数，它与诸多工业问题密切相关，而表面张力系数又不是一个固定的数值，随工质的温度，压力等因素变化.本文采用数值模拟方法来研究表面张力系数的变化对气泡作用的影响.

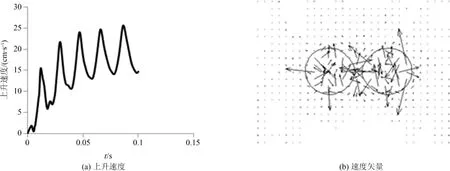
图4 两气泡上升速度和速度矢量Fig.4 Vertical velocity and velocity vector distribution of two bubbles

2.3.1 改变表面张力，气泡融合的情况

改变表面张力系数，分别取σ1＝0.1σ0，σ0，5σ0，10σ0，这四种情况下，两气泡在上升的过程中发生融合.气泡上升速度随时间变化如图5所示.σ1＝0.1σ0时两个气泡融合后速度波动不大，如图5（a）所示.σ1＝5σ0时，两个气泡融合后速度变大，波动也更为剧烈.σ1＝10σ0时的情况和σ1＝5σ0时的类似.两个气泡在接触后融合成一个更大的气泡，在上升过程中，气泡的形状震荡，速度也在波动，从图5中可以看出，随着表面张力系数σ的增大，融合后的气泡速度震荡的更加剧烈，幅度也更大，且平均上升速度呈上升趋势.

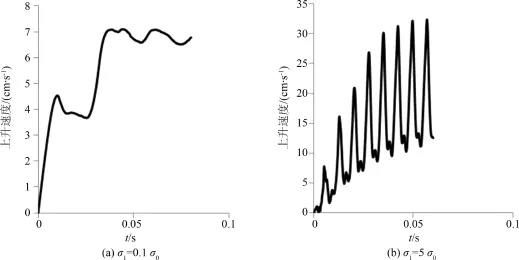
图5 气泡上升速度随时间变化Fig.5 Vertical velocity of coalescence bubbles

2.3.2 改变表面张力，气泡分离的情况

改变表面张力系数，分别取σ2＝0.04σ0，0.02σ0，0.01σ0，0.005σ0，这四种情况下，两个气泡独立上升，均不会融合.在以往的研究中，大都是针对气泡的形状变化进行模拟研究，很少对气泡运动轨迹进行研究，本文采用数值方法，再现了两气泡在相互作用过程中质心轨迹的变化.未融合情况下，两个气泡质心的运动轨迹如图6所示.为了研究气泡之间的相互作用对单个气泡运动的影响，图6也给出了右气泡单独存在时的运动轨迹.从图中可以看出，随着表面张力系数的减少，单个右气泡的上升轨迹水平波动越来越小，到后面近似呈直线上升，而且气泡之间的相互作用加剧了右气泡的波动程度.从图中还可以看出，单气泡上升的距离更大，说明另一个气泡的存在减小了气泡的平均上升速度.

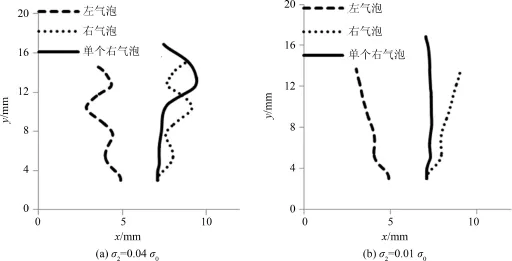
图6 气泡质心轨迹Fig.6 Trajectory of single bubble and a pair of bubbles

并排气泡对的上升过程出现了两种运动类型：反复靠近⁃远离⁃靠近但未融合（σ2＝0.04σ0），如图6（a）所示；碰撞反弹后相距越来越远（σ2＝0.02σ0，0.01σ0，0.005σ0），这三种情况下运动轨迹类似，如图6（b）所示.表面张力较小时，两个气泡在上升过程中出现靠近－远离－再靠近的周期性现象，这与李彦鹏模拟水中8mm气泡对的研究结果［15］相类似.可见，气泡直径增大与表面张力系数减小的效果类似，这是因为气泡直径的增大同样会引起所受表面张力的减小.表面张力继续变小时，两个气泡在上升过程中水平距离越来越大，并没有出现靠近的现象，如图6（b）所示，在Sone［8］的实验中也观察到了同样的现象.气泡对之间反复出现靠近－远离－靠近的现象，主要是因为高Re数下，气泡尾部出现了涡旋的脱落，它们之间的相互作用导致了气泡对的运动轨迹出现波动［1］，如图7所示.而随着表面张力系数的减小，气泡尾迹的相互作用表现为排斥力作用，导致两气泡逐渐远离.

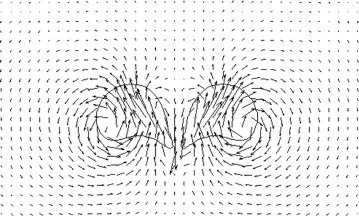
图7 两气泡速度矢量（σ2＝0.04σ0）Fig.7 Velocity vector distribution of two bubbles

并排气泡和单个右气泡独立存在时的上升速度如图8所示.可以看出，对于单个右气泡的独立上升，气泡的上升速度先增大，后呈波动状态.对于并排上升气泡对而言，左右两个气泡上升速度基本完全一致均呈波动状态，但比单个气泡独立上升时的速度小.可见气泡之间的相互作用减小了气泡的上升速度.

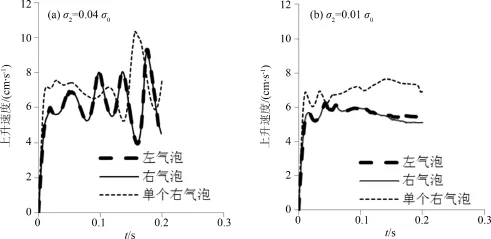
图8 气泡上升速度随时间变化Fig.8 Vertical velocity of single bubble and a pair of bubble

从图8中可以看出，随着气泡的上升，并排气泡上升速度不断增大，后面开始震荡，而且随着表面张力系数的减少，震荡的频率和幅度均下降.上升初期，两个气泡不断靠近，上升速度也在逐渐增大，相互靠近到某一距离时，两气泡开始反弹，此时，上升速度显著下降，之后呈波动状态.

气泡水平速度随时间变化如图9所示.右气泡单独上升时，其水平速度并不为零而且呈波动状态，从而解释了其上升轨迹水平方向有波动的原因.从图中可以看出，并排上升两气泡的水平速度大小相等，方向相反，而且同样也呈现出波动状态.随着表面张力系数的减小，单个气泡水平速度波动的幅度和频率均减小，两个并排气泡的水平速度也是如此.另一个气泡的存在加剧了右气泡的水平波动，这也解释了两气泡并排上升时对称波动上升的轨迹特征.

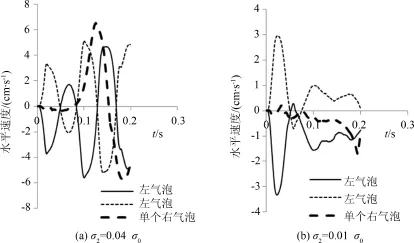
图9 气泡水平速度随时间变化Fig.9 Horizontal velocity of single bubble and a pair of bubbles

2.3.3 结果分析

从前面两种情况可以看出，存在一个临界的表面张力系数σcr，因此选择更多的表面张力值，分别取σ＝0.09σ0、008σ0、0.007σ0，当 σ＝0.09σ0时气泡融合，其它两种情况下两个气泡不会融合，可见 σcr约为0.09σ0．在常见的液态工质中，液态金属和熔融盐以及水的表面张力比较大，是大于这个范围的，这些工质中的气泡更容易融合.汽油、乙醚等有机溶液表面张力较小，在这些工质中气泡不易融合.

在两气泡的相互作用过程中，液桥是一个重要的因素.液桥力主要是由气－液相界面的表面张力和液桥内外的压力差引起的［16］.因此，改变表面张力系数，两气泡的作用过程会出现不同的结果.

3 结论

1）采用VOSET方法模拟了并排气泡对在竖直通道内的相互作用过程，模拟结果与相关文献和实验吻合较好.

2）改变表面张力系数，气泡对出现了三种运动类型.较大的表面张力系数下，气泡发生融合，融合后形成一个更大的气泡上升，融合后的气泡没有稳定的形状，也没有稳定的上升速度；中等表面张力系数时，两气泡没有融合，在上升过程中出现反复靠近－分离－再靠近的运动特征；较小表面张力系数下，两个并排气泡未发生融合，碰撞反弹后相互远离，排斥上升，在上升的过程中，二者的水平距离越来越大.

3）气泡对的相互作用过程中，如果没有融合，则两个气泡的上升速度基本一致，和单个气泡的上升速度相比较，均有所下降但变化趋势基本趋势一致，和水平速度相比差异较大.从而可以看出，两气泡的相互作用主要影响气泡对的水平运动，对竖直方向的运动影响不大.

［1］ Sanada T，Sato A，et al.Motion and coalescence of a pair of bubbles rising side by side［J］.Chemical Engineering Science，2009，64（11）：2659－2671.

［2］ Duineveld PC.Bouncing and coalescence of bubble pairs rising at high Reynolds number in pure water or aqueous surfactantsolutions［J］.Appl Sci Res，1998，58：409－439.

［3］ 张淑君，吴锤结.气泡之间相互作用的数值模拟［J］.水动力学研究与进展：A辑，2009，（6）：681－686.

［4］ 赵知辛，王焕然，李彦鹏，等.用Level Set方法对水下两个气泡运动的数值模拟［J］.西安交通大学学报，2009，43 （7）：11－15.

［5］ Chen R H，Tian W X，et al.Numerical investigation on coalescence of bubble pairs rising in a stagnant liquid［J］.Chemical Engineering Science，2011，66（21）：5055－5063.

［6］ 王太，李会雄，李阳.同轴两个气泡融合特性的数值研究［J］.西安交通大学学报，2013，47（7）：1－6.

［7］ Wu M，Gharib M.Experimental studies on the shape and path of small air bubbles rising in clean water［J］.Physics of Fluids，2002，14（7）：L49－L52.

［8］ Sone D，Sakakibara K，et al.Bubblemotion and its surrounding liquid motion through the collision of a pair of bubbles［J］. Journal of Power and Energy Systems，2008，2（1）：306－317.

［9］ Sun D L，TaoW Q.A coupled volume⁃of⁃fluid and level set（VOSET）method for computing incompressible two⁃phase flows ［J］.International Journal of Heat and Mass Transfer，2010，53（4）：645－655.

［10］ 叶政钦，刘启鹏，李星红，等.复杂两相流中界面追踪方法——VOSET的性能分析［J］.化工学报，2011，62（6）：1524－1530.

［11］ Brackbill JU，Kothe D B，et al.A continuum method for modeling surface tension［J］.Journal of Computational Physics，1992，100（2）：335－354.

［12］ Osher S，Sethain JA.Fronts propagating with curvature dependent speed：Algorithms based on Hamilton Jacobi formulations ［J］.JComput Phys，1988，79：12－49.

［13］ Sun D L，Qu ZG，et al.An efficient segregated algorithm for incompressible fluid flow and heat transfer problems—IDEAL （inner doubly iterative efficient algorithm for linked equations）Part I：Mathematical formulation and solution procedure［J］. Numerical Heat Transfer，Part B：Fundamentals，2008，53（1）：1－17.

［14］ Fan L S，Tsuchiya K.Bubble wake dynamics in liquids and liquid⁃solid suspensions［M］.Boston，Massachusetts，USA：Butterworth⁃Heinemann，1990：263－270.

［15］ 李彦鹏，张乾隆，白博峰.竖直通道内相邻气泡对上升的直接数值模拟［J］.热能动力工程，2007，22（4）：375－379. ［16］ 韩笑.气固流化床中持液颗粒的流化特性及反应器模型研究［D］.杭州：浙江大学，2013.

Simulation of a Pair of Bubbles Rising Side by Side Using VOSET M ethod

LILongjian，ZHANG Lei，ZHUWenbing，SHEN Xianwen
（College of Power Engineering，Chongqing University，Chongqing 400030，China）

A numerical simulation was performed to investigate two bubbles rising side by side in vertical channel using VOSET （Coupled Volume⁃of⁃Fluid and Level Set）method and N⁃Sequations coupled with continuous surface force（CSF）model.Behaviors of coalescence between two identical bubbles predicted were in good agreementwith experimental results reported in literature.Effects of surface tension on trajectories and velocities during rising process are investigated.Three types ofmotion were observed depending on surface tension：Coalescence，two bubbles repeatedly attracted and bounced against each other，bounced and separated.Without coalescence，trajectory shows symmetry about channel center line.Vertical velocities of both bubbles are almost the same while magnitude of horizontal velocity with opposite direction equals.

bubble pairs；numerical simulation；VOSET

O359＋.1

A

2014－09－02；

2014－12－08

国家自然科学基金（51076172）资助项目

李隆键（1966－）男，博士，教授，主要从事气液两相流的数值模拟研究，E⁃mail：longjian＠cqu.edu.cn

Received date： 2014－09－02；Revised date： 2014－12－08