基于局部傅里叶变换的相位提取方法研究

蔡长青，张永山

（广州大学 土木工程学院，广东 广州 510006）

基于局部傅里叶变换的相位提取方法研究

蔡长青，张永山

（广州大学 土木工程学院，广东 广州 510006）

基于在被测物加载前后分别采集5幅散斑干涉图的10图五步相移法,需要在物体加载后采集5幅散斑图,通常只适用于静态测量.基于在被测物加载前采集5幅散斑图,采集变形后1幅散斑图的6图五步相移法,得到的相位图噪声很多,质量较差.为了克服上述两种方法各自的缺点,即寻求一种既能得到高质量相位图,又能应用于动态测量的方法,本文提出了将局部傅里叶变换方法与6图五步相移法相结合的新方法.实验验证表明该方法能够明显地提高相位图的质量.

相位提取；局部傅里叶变换；降噪；6图五步相移法

1 引言

电子散斑干涉术(Electronic speckle pattern interferometery,简写为ESPI)因具有全场、非接触、高精度、实时性和抗振性好等特点而被广泛应用于材料弹性模量测量[1]、表面粗糙度评价[2]、应力应变分析[3]、振动分析[4]和无损检测[5]等领域.电子散斑干涉术测量结果通常以干涉条纹的形式表现出来,与被测物理量直接相关的是蕴涵于干涉条纹中的相位信息.准确地提取相位在应用ESPI获得物体变形位移信息中起着非常重要的作用.通常由实验获得的相位图在很大程度上受到噪声的影响,所以相位提取方法的研究就显得尤为重要.相移技术就是相位提取的重要方法之一.

基于在被测物加载前后分别采集5幅散斑干涉图的10图五步相移法[6-8],由于能够得到高质量的相位图而被广泛应用于光学图像的相位提取.但该相位提取方法需要在物体加载后采集5幅散斑图,通常只适用于静态测量.基于在被测物加载前采集5幅散斑图,采集变形后1幅散斑图的6图五步相移法[9-10],由于在物体变形后只需采集1幅散斑图,因而具有应用于振动或动态测量的可能.相比于10图五步相移法得到的相位图,6图五步相移法得到的相位图噪声很多,质量很差.为了克服上述两种方法各自的缺点,即寻求一种既能得到高质量相位图,又能应用于动态测量的方法,本文提出了将局部傅里叶变换[方法与6图五步相移法相结合的新方法.实验验证表明该方法能够明显地提高由6图五步相移法得到的相位图质量.

2 五步相移原理

2.16幅光强图的五步相移法

在被测物未加载时引入四步相移,采集5幅光强图,其量值为

其中:a为背景光强,b为调制度.

对被测物加载,则得到如下光强图:

为了求得相位变化β,将变形前的5幅光强图分别与变形后的光强图相减,得到5幅相减图像,分别为:

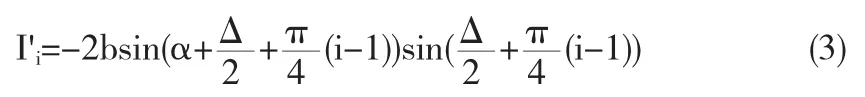
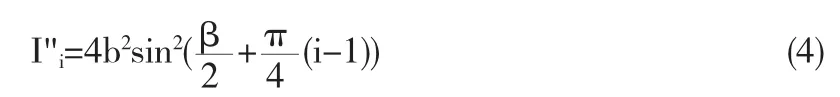
根据五步相移法,由式(4)可得相位角的正切表达式为:

2.210幅图像的五步相移法

在被测物未加载时引入五步相移,得到的5幅图像的光强图分别为:

对被测物加载,并同样引入五步相移,则得到5幅光强图为:

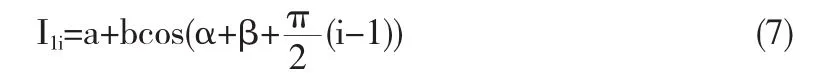
根据三角函数原理,可将变形前后的相位分布表达为反正切形式为:

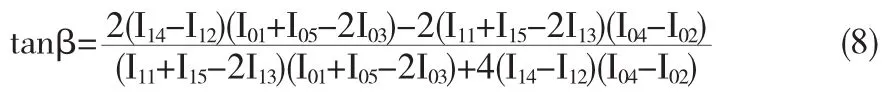
3 局部傅里叶变换原理

局部傅里叶变换(Localized Fourier Transform)是一种在频域内对图像进行降噪的简单方法.首先将图像用小窗口分为小的子区域w×w,然后对这些小的子区域进行傅里叶变换.操作过程和结果可由下式表示:

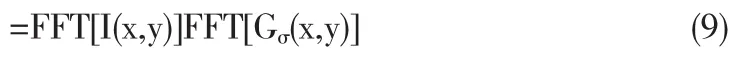
其中,Gσ(x,y)=exp[-(x2+y2)/σ]/πσ,||Gσ(x,y)||=1.

由于高斯函数Gσ(x,y)的傅里叶变换为:

将式(10)代入式(9)可以得到:

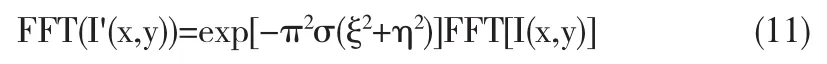
为了得到高质量的滤波图像,需要将傅里叶变换频域的频谱系数进行处理.由于有用的图像信息得到的频谱系数大,而由噪声得到的频谱系数通常很低,但由于二者得到的频谱系数并没有一个明确的界限,本方法采用对频谱系数进行指数操作,达到对小的频谱系数进行抑制,而对大的频谱系数进行增强.如下式所示:

对式(12)进行局部傅里叶逆变换就可以得到高质量的图像.如下所示:

局部傅里叶变换滤波的效果与区域尺寸w×w的选取和系数α和σ有关.滤波后通常会得到高质量的相位图.

4 实验验证

为了验证本文提出的相位提取的可行性,进行了对周边固支中心加载的圆盘模型的离面位移导数进行测量的实验.在加载前采集5幅散斑干涉图,相移量分别为和2π.加载后同样采集5幅散斑干涉图,相移量分别为0,,和2π.将局部傅里叶变换滤波分别对上述两种方法得到的相位图进行滤波处理,得到结果如下.其中,图1(a)和(b)分别是由五图四步相移法和八图四步相移法得到的相位图.图2(a)和(b)分别是对应图1(a)和(b)进行局部傅里叶变换滤波后的结果.对比图1和图2可知,局部傅里叶变换滤波方法与四步相移法相结合,可明显地提高相位图质量,特别是与五图四步相移法结合使用时,有可能成为动态测量的一种新方法.

图1　五步相移相位图

图2　五步相移与局部傅里叶变换滤波的相位图

5 结论

为了寻求一种既能得到高质量相位图,又能应用于动态测量的方法,本文提出了将局部傅里叶变换方法与6图五步相移法相结合的新方法.该方法在被测物加载前采集5幅散斑图,采集变形后1幅散斑图,分别用6图五步相移法和局部傅里叶变换滤波法进行处理,从而得到高质量的相位图,实验验证表明该方法能够明显地提高由6图五步相移法得到的相位图质量.

〔1〕Viotti M R,Kaufmann G H,Galizzi G E.Measurement of elastic moduli using spherical indentation and digital speckle pattern interferometry with automated data processing[J].Optics and Lasers in Engineering,2006,44(6):495-508.

〔2〕Dhanasekar B,Ramamoorthy B.Digital speckle interfer-ometry for assessment of surface roughness[J].Optics and Lasers in Engineering,2008,46(3):272-280.

〔3〕Yang L X,Ettemeyer A.Strain mearement by three dimensional electronic speckle pattern interferometry potentials limitations and applications[J].Optical Engineering,2003,42(5):1257-1266.

〔4〕Yang L X,Schuth M,Thomas D,et al.Stroboscopic digital speckle pattern interferometry for vibration analysis of microsystem [J].Optics and Lasers in Engineering, 2009,47(2):252-258.

〔5〕Esteban Andres Zarate,Eden Custodia G,Carlos G,et al.Defect detection in metals using electronic speckle pattern interferometry[J].Solar Energy Materials&Solar Cells,2005,88(2):217-225.

〔6〕Huntley J.M.,Saldner H..Temporal phase-unwrapping algorithm for automated interferogram analysis [J].Applied Optics,1993,32(17),3047-3052.

〔7〕Stetson K.A..Theory and applicationsofelectronic holography [J].Proceedings of the International Conference on Hologram Interferometry and Speckle Metrology,1990,Bethel,Conn.,294-300.

〔8〕Kemao Q.Two-dimensional windowed Fourier transform for fringe pattern analysis:principles,applications and implementations[J].Optics and Lasers in Engineering,2006,44(3),304-317.

〔9〕Ritter R,Galanulis K,Winter D,Muller E,Breukmann B.Notes on the application of electronic speckle pattern interferometry [J].Opticsand Lasersin Engineering, 1997,26(5),283-299.

〔10〕Pena RG,Anda RMCOD,Velazquez AJP,Cruz JSDL,Jorge YG.Displacement measurements in structural elements by optical techniques[J].Optics and Lasers in Engineering,2000,34(4),75-85.

TN919；O436

A

1673-260X（2015）12-0022-02

国家自然科学基金（51378135）；广州大学2013年新苗计划项目（CCQ1-1407）；广州大学引进人才科研启动项目（2221）