一道高考题引发的思考
宁夏中卫市第一中学 刘前进
2014年普通高等学校招生全国统一考试(课标Ⅱ)文科数学选择第10题:设F为抛物线C∶y2=3x的焦点,过F且倾斜角为30°的直线交C于A,B两点,则|AB|=( )

理科数学选择第10题:设F为抛物线 C∶y2=3x的焦点,过F且倾斜角为30°的直线交C于A,B两点,O为坐标原点,则 △OAB的面积为( )
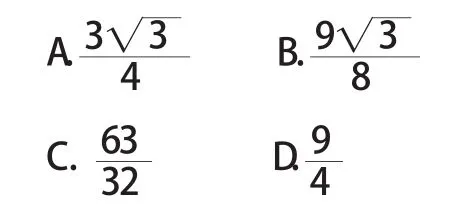
上面两道题目都是与过抛物线焦点的弦长有关的问题,文理科其实是同一道题目,我们先看与之有关的两个常用结论的推导.
已知抛物线的方程为y2=2px(p>0),过焦点F且倾斜角为θ的直线交抛物线于A,B两点,求弦AB的长及△OAB的面积.
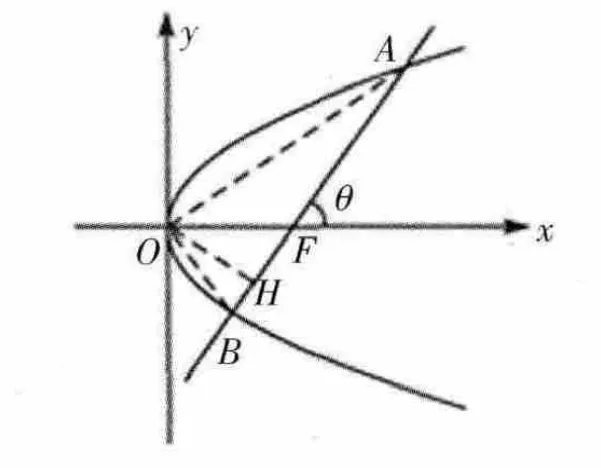
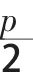

由点到直线的距离公式得:
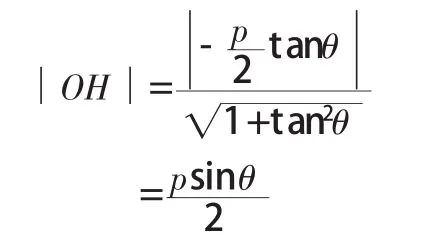
∵y1,y2是方程①的两根,
∴由根与系数的关系得:
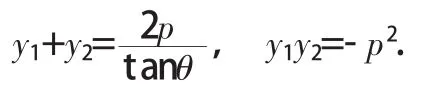
由弦长公式得:

当 θ=90°时,AB⊥x轴,
由抛物线定义,知|AB|=2p,
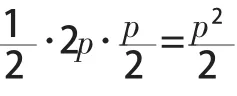

以上证明的就是课外资料书上总结的抛物线的焦点弦长公式以及点O,A,B三点围成的三角形的面积公式:
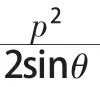
利用这两个结论,将题目中的已知数据代入可以快速得到答案,但是如果不知道这两个结论,这两个题目只能按照上面的推导过程来求解,你可以试一下,本题的数据计算起来非常烦琐,学生在高考考场上得花大量时间才能求出结果,甚至更多的学生如果计算能力不过关,很难得到正确答案.通过这两道题目,我们应该思考:在以后的教学中不仅仅是就课本内容而讲解解题方法,不仅仅是只让学生记忆课本上的公式和结论,对于课外资料书上总结的常见、常用的数学结论教学时应该介绍给学生,甚至可以根据学生的学情在课堂上来推导一下结论.利用这些结论,做选择题、填空题时可以迅速准确解答,为学生节省大量的时间去做其他的题目,我们知道,高考考场上时间就是分数,一分一秒非常宝贵,尤其是数学科目,两个小时做完22道题目是非常紧张的,每年高考结束反映最多的就是数学科目时间不够,题目没有做完.因此,这两道高考题目应该引发我们在今后的教学中课内外知识的融合是必要的,同时在解题方法上除了通法外,也要训练学生直接利用一些重要的数学结论解题,只有两种方法同时训练,学生在高考考场上才能有意识利用最简捷的方法解题.
杨建新.抛物线过焦点的弦长公式及其应用[J].数学通讯(上半月).2011(3)

