基于学生化残差计算的变形监测资料奇异值检验
李行洋,李 珩
(1.湖北水利水电职业技术学院,武汉 430070;2.华中农业大学,武汉 430070)
变形监测,是利用测量专用仪器、方法对变形体的变形现象进行监测观测的工作,具有重复性特征。当在相同观测条件下对某量进行重复观测时,如果不是变形体非实质性的变化,而观测误差超出规定条件的预期,出现粗大误差或粗差。含有粗大误差的测量值即为异常值,也称离群值或坏值[1]。测量中,将含有粗大误差的测量值也称为奇异值。粗大误差的存在不仅大大影响测量成果的可靠性,而且给工作带来难以估量的损失[2]。在进行监测数据处理前,需要用一定方法判断测量列中是否含有粗大误差,并将含有粗大误差的奇异数据进行剔除,再利用余下的正常数据对测量误差参数进行估计。相关文献[3~4]提出了两种利用观测数据序列级差来判别奇异值的方法,但计算工作量大且判别的准确性有待进一步研究。其他常用的粗大误差的统计判别准则还有拉伊达准则、格拉布斯准则、肖维勒准则、狄克逊准则等[5],其中,拉伊达准则又称为“3σ”准则,当观测次数小于10时,通常认为其判别含有粗大误差的可疑数据的可靠性不高;肖维勒准则与拉伊达准则的判别思路相似,但判别结果较为苛刻;格拉布斯准则判别结论则与置信水平的选择有着极大关系[6],且需要区分异常值为上侧或下侧、单侧或双侧等情况;而狭克逊准则是直接根据测得值的顺序统计量按级差比方法进行判别,也存在计算复杂的问题。本文介绍学生化残差的蒙特卡洛模拟法、精细准则、X2检验法,通过对变形监测数据实例进行奇异值检验,认为基于学生化残差计算的变形监测资料奇异值检验方法既具有直观性、有效性,而且还可以大大地减少计算工作量。
1 学生化残差检验法
1.1 学生化残差
设对某量进行n次独立观测,得到测量数据序列xi(i=1,2,…,n),则其算术平均值为

而残差分别为

观测值均方差估值为

构造统计量

式中,yi为实验学生化残差,一般情况下可简称为学生化残差。
1.2 最大实验学生化残差的统计分布函数

积分区域Ω满足

式中,a为选定的残差限值,σ为观测值的均方差。
参数a的取值范围为

1.3 学生化残差的蒙特卡洛模拟检验法
蒙特卡洛法的基本思想是,对于某一问题,建立与描述该问题相似的概率模型,并对模型进行随机模拟或统计抽样,即产生一组分布与随机模型相同的随机数,并以该随机数的统计特征作为原始问题的近似解。
按照学生化残差的蒙特卡洛模拟,设有n(n=3,4,…,50)个独立服从N(0,1)分布的随机数,从中可以找出1个最大学生化残差绝对值;如分别取出1 000 000n(n=3,4,…,50)个独立服从N(0,1)分布的随机数,则依次可产生1 000 000个将此作升序排列且记为(y1,y2,…,y1000000),取的阶梯经验分布函数作为分布函数F(x)的估计,即
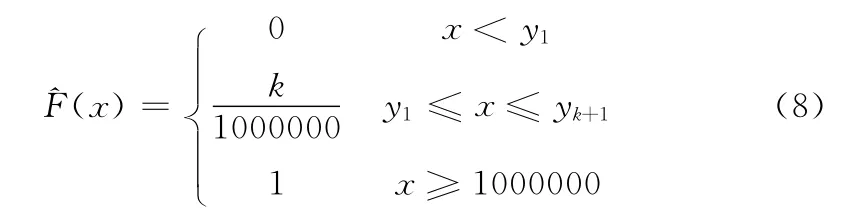
经验分布函数具有单调非降、右连续及其他许多离散型随机变量分布函数的一切性质,当样本容量充分大时,其与母体分布函数相当接近。
按置信水平α=0.01或α=0.05研究经验函数^F(x)分别取0.99、0.95时所对应的x值,即可构成学生化残差绝对值法剔除异常值的临界值表1。

表1 学生化残差绝对值临界值表
在给定显著性水平α下,查出临界值L1-α(n);当yi>L1-α(n)时,认为 max|vi|对应的xi为奇异值,应剔除。否则,认为该观测序列中不包含有奇异值。
1.4 学生化残差的精细检验法
设测量数据序列xi(i=1,2,…n)服从N(μ,σ2),则服从汤普逊τ(n-2)分布,其概率密度函数为

最大实验学生化残差的统计分布函数满足
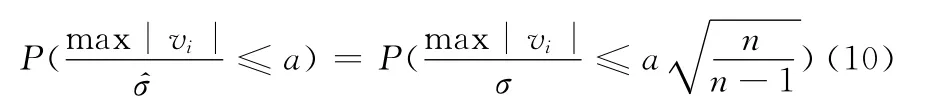
刘智敏[7]计算出最大实验学生化残差绝对值的临界值见表2。

表2 精细准则临界值表
在给定显著性水平α下,若统计量

则认为对应的观测值xi是奇异值,应予剔除;否则,认为该观测序列中不包含有奇异值。
1.5 学生化残差的X2检验法
设测量数据序列xi(i=1,2,…,n)服从N(μ,σ2),由(4)式,得

显然,当vi较大时,其对的影响也较大,也就是的数值会增大。
考虑到

即有

故


在给定的显著性水平α下,如,则认为测量列xi(i=1,2,…,n)中有奇异值存在,应剔除 max|vi|对应的xi。否则,认为该观测序列中不包含有奇异值。
2 变形监测资料奇异值检验实例分析
实例1。表3为某水利枢纽大坝J22-20测点横缝开度年最大值的观测数据,假定观测条件如年水位、温度无显著特殊变化,取置信水平α=0.01,现分析该观测资料中是否存在奇异值。

表3 J22-20测点横缝开度年最大值 单位:mm
分别用拉伊达准则、格拉布斯准则、肖维勒准则、狭克逊准则进行判别,观测序列数据中无奇异值存在;按文献[3]介绍的两种利用观测数据序列级差来进行判别,未发现观测序列数据中有奇异值存在;利用学生化残差的蒙特卡洛模拟检验法、精细检验法、X2检验法分别进行检验,观测序列数据中亦无奇异值存在。直观来看,该观测序列数据较为均匀,而无论采用上述介绍的何种方法,皆得出了相同的检验结论。
实例2。表4为某水利枢纽大坝19#坝段一测点正垂线一天中8个整时间点的切向位移观测数据,取置信水平α=0.05,现分析该观测资料中是否存在奇异值。

表4 切向位移观测数据 单位:mm
利用拉伊达准则、狭克逊准则、学生化残差的X2检验法及文献[3]介绍的两种利用观测数据序列级差来进行判别,未发现观测序列数据中有奇异值存在;而利用格拉布斯准则、肖维勒准则、学生化残差的蒙特卡洛模拟检验法、精细检验法分别进行检验,发现该观测序列中第6个观测数据是奇异值。
从上例试算来看,对同一问题如采用不同准则进行检验,可能得出不同的判别结果。比较其中几种检验方法的临界值,在同一置信水平前提下,拉伊达准则要求较低,因此存在“漏判”的概率比较大;学生化残差的X2检验法对于观测数据的“波动”不是很明显时,其判别奇异值的灵敏度也不高,也可能存在“漏判”的情况;肖维勒准则要求较为苛刻,因此可能存在“误判”的情况;狭克逊准则及文献[3]介绍的两种利用观测数据序列级差判别法,不仅计算较为复杂,亦可能存在“漏判”的情况;而格拉布斯准则、学生化残差的蒙特卡洛模拟检验法、精细检验法,都是直接考虑“大”残差的情况,因此,检验效果较为可靠。
如进一步比较格拉布斯准则、学生化残差的蒙特卡洛模拟检验法、精细检验法这三种检验方法,可以发现它们的检验思路有些类似,而且临界值大小区别不甚明显,但学生化残差的蒙特卡洛模拟检验法、精细检验法计算的直观性更强,特别是在样本量不是太大的情况下,蒙特卡洛模拟检验法与精细检验法的临界值几乎一样。
在上例中,如剔除第6个观测数据后再计算观测值的均方差则为0.0331mm,与原观测系列计算结果相比较,虽然观测值的个数减少了,但观测值的精度反而提高了。由此说明,在观测数据处理中,适当的“严格”远比“漏判”更为有利。
3 结 语
变形监测原始数据,是进行变形分析的重要基础。对变形监测原始数据是否存在奇异值进行检验判别,无疑有着重要意义。对于同一问题,采用不同的判别准则可能会得出不同的判别结果。从实践来看,传统的一些检验方法不是计算工作量太大,就是检验灵敏度不高。为了尽可能避免出现对变形监测原始数据“漏判”、“误判”的情况,在样本量不是很大的情况下,采用学生化残差的蒙特卡洛模拟法、精细检验法、X2检验法进行检验具有较强的直观性、简便性。特别是当观测数据并不呈现特别跳跃性“波动”时,蒙特卡洛模拟法、精细检验法的有效性非常明显;而当观测数据呈现特别跳跃性“波动”时,X2检验法的有效性也将进一步显现。
[1]费业泰.误差理论与数据处理[M].北京:机械工业出版社,1987.
[2]於宗俦,鲁林成.测量平差基础[M].北京:测绘出版社,1983.
[3]黄声享,等.变形监测数据处理[M].武汉:武汉大学出版社,2003.
[4]王怀义,卢新民,吴 艳,等.乌鲁瓦提混凝土面板坝安全监测数据处理系统[J].土坝观测与土工测试,2003,(3):29-32.
[5]熊艳艳,吴先球.粗大误差四种判别准则的比较和应用[J].大物理实验,2010,(1):66-68.
[6]董海鹏,花春飞.在大学物理实验中应用格罗布斯准则判定粗大误差[J].牡丹江大学学报,2011,(3):128-129.
[7]刘智敏.残差性质及其应用[J].计量学报,1980,(1):198-212.

