五自由度并联机构正解新数值算法

张永文

（广西大学机械工程学院，广西 南宁530004）

由于并联机构结构的复杂性，并联机构的位置正解的求解难度大，主要求解方法有解析法和数值法[1]。由于并联机构正解解析法理论发展尚不成熟，数学推导过程复杂，而且通用性不高，因此一般采用数值算法求解。目前并联机构数值求解算法主要有两类：一类是使用Newton-Raphson法[2-5]。例如Lee、Warldron、Pfreundschum等的研究中，基于并联机构运动学正解方程，用牛顿迭代法对并联机构正运动学进行求解。这种数值算法需要计算机构雅克比矩阵及其逆阵，计算量大，计算时间相对较长[6]，且算法收敛性对迭代初始值比较敏感，不利于实时控制；另一类算法是基于并联机构的逆解，但不用计算雅克比矩阵来求机构正解[7-9]。例如神经网络算法、遗传算法等等。这类算法避免了复杂的公式推导和编程工作，但是求解精度难以满足并联机构实时控制要求。对此，本文以五自由度并联机构为研究对象，提出一种新的并联机构正解数值算法。

1 问题描述和现有正解数值算法

1.1 问题的描述

研究的五自由度并联机构如图1所示，该机构由静平台、动平台和五个支链组成。五个支链中有四个支链结构相同，由转动副、万向节和球副组成，其与动、静平台铰接点位于以动、静平台中心点为中心对称点的长方形的四个角点；另一个支链由一个连杆和一个四连杆串联构成。机构所有转动副轴线相互平行，且支链中万向节的一个转动轴线也始终与转动副轴线平行，P点和O点分别是动、静平台的中心。以动平台中心P点为原点建立右手坐标系P-XPYPZP，其中XPPYP平面与动平台重合，XP、YP轴方向为垂直于动平台相邻铰节点连线方向。以静平台中心点O为原点建立右手坐标系O-XOYOZO，XOOYO平面与静平台重合，XO轴方向与机构转动副轴线方向平行。机构结构尺寸 Li（i=1，2，3…12）如图 1 中所示。

图1 五自由度并联机构结构示意图

设动平台位姿由（PxPyPzαβγ）六个参数来表示，其中 Px、Py、Pz表示动平台中心点的坐标，α、β、γ表示动坐标系相对于静坐标系的XYZ欧拉角。

1.2 现有正解数值解法——New ton-Raphson迭代法

Newton-Raphson迭代法基于并联机构运动学正解方程组，用牛顿迭代法对并联机构正运动学进行求解。动平台上一点在静坐标系中坐标可由坐标变换求得：

式中:Pp为动平台中心点在静坐标系中的坐标；

由式（1）可求得bi（i=1，2，3，4）在静坐标系boi（i=1，2，3，4）中的坐标，由 biDi杆和 FP 杆长可列方程组：

将式（2）用动平台位姿参数表示为：

式（3）就是五自由度可控并联机构的正解方程组，该方程组具有强非线性，很难求得解析解，利用Newton-Raphson数值迭代法可求得方程组的解，即五自由度并联机构的正解。

2 新算法

2.1 新算法的基本思路

新算法是基于图形相似理论[10]提出来的，其基本思路如下：

（1）初取迭代初始值。在五自由度并联机构工作空间内任取一点作为迭代的初始值：

（3）修正P、bi（i=1，2，3，4）.由迭代初始值求出的动平台铰接点不一定是动平台铰链点真实位置，机构结构参数PF=L10与boiDoi=L6不一定成立，为此作如下修改：

式中：P（2）为新动平台上的P点，M点和N点为新引入的两个点，分别为b1与b2点的连线中点、M点与 N 点的连线中点，由点唯一的确定了一个新动平台平面。

（5）提取新动平台姿态参数。

根据N点和P（2）点坐标可求解新动平台姿态参数 α（2）、γ（2）和 β（2）：

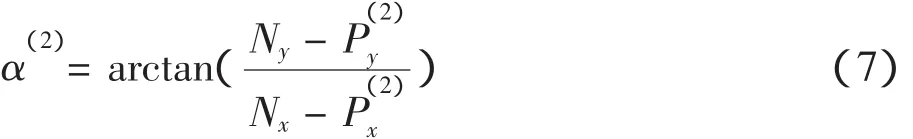
为了进一步求解 γ（2）和 β（2），先将法线向量ny，nz）绕基坐标Zo轴逆时针旋转-α（2）角得一个中间法线向量，如下：

根据中间法向量n軋1（n1x，n1y，n1z）可直接求得γ（2）和 β（2）：

如果式（10）不成立，则以求得的新动平台位姿参数为新的迭代初始量进入下一轮迭代，直至式（10）成立，即求得了并联机构位置正解，其求解流程图如下图2所示。

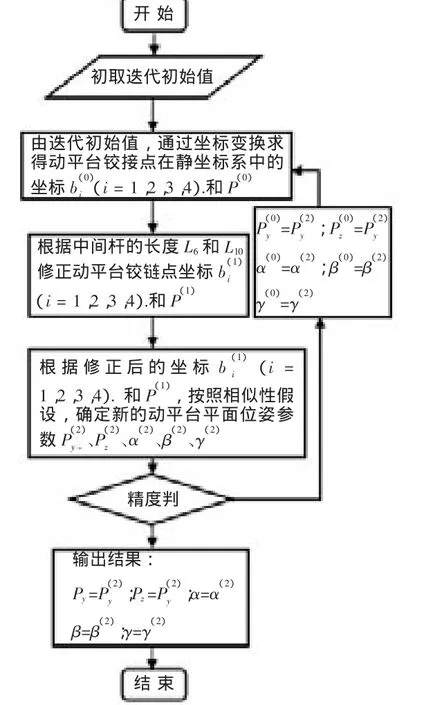
图2 新算法流程图

2.2 数值试验和算法性能对比

并联机构正解数值求解过程中使用Newton-Raphson迭代法是目前比较常用的算法。本文将新算法与Newton-Raphson迭代法的性能进行对比，以总结新算法的特点和评价新算法的优劣。

五自由度并联机构结构参数如下表1所示。利用同一台电脑上的matlab软件平台用上述两种数值解法对五自由度并联机构正解数值求解进行编程，先后输入机构两个位置的驱动副输入量，初取同一迭代初始值，进行数值试验，并与在ProE软件分析模块中测得的结果作对比，试验结果如表2至表5所示。

表1 五自由度并联机构结构参数

表2 牛顿拉斐逊迭代法位置一计算结果

表3 新算法位置一计算结果

表4 牛顿拉斐逊迭代法位置二计算结果

表5 新算法位置二计算结果

根据数值实验数据分析：

（1）对比表2与表3，可知Newton-Raphson迭代法在迭代初始值适当时，单步迭代收敛速度快，但单步平均迭代时间相比新算法长。而新算法相反，每次迭代收敛速度慢，几乎每迭代80次仅相当于牛顿拉菲讯法迭代一次，但是新算法每次迭代所需时间极短，且总的来说两种迭代法计算收敛到预定精度所需总时间对比，新算法更少；

（2）对比表1与表3可知牛顿-拉菲讯法对迭代初始值的选取比较敏感，迭代初始值没选好很可能会导致迭代收敛速度减缓甚至迭代不收敛；而对比表2与表4可知新算法对初始值的选取并不敏感，具有良好的适应性；

3 结束语

本章以五自由度可控并联机构为研究对象，提出一种新的五自由度并联机构正解求解数值方法，新算法基于图形相似理论[10]，求解思路简单，求解过程中不需要求机构的雅克比矩阵及其逆阵。通过进行编程和数值实验和实验数据分析，将数值实验所得数据与在Pro/E机构分析中测得的数据进行对比分析，验证了所采用的这两种数值分析方法的正确性，总结出这新算法初值敏感度低、单步迭代时间短，达到预定求解精度所需的迭代求解总时间短、编程工作量少等基本特点，有利于适时控制，且本算法可以推广到其它相似结构的并联机构，具有较大的应用前景。

[1]黄 真.高等空间机构学[M].北京：高等教育出版社，2006.

[2]Lee K，Shah KD.Kinematic analysis of a three degrees of freedom in-parallel actuated manipulator[J].Journal of Robotics and Automation，1988，4（3）:361-367.

[3]Waldron KJ，Raghavan M，Roth B.Kinematics of a hybrid series-parallel manipulation system[J].ASME Journal of Dynamic Systems，Measurement and Control，1989，111（2）:211-221.

[4]Hashimoto Minoru，Imamura Yuichi.Kinematic analysis and design of a 3 DOF parallelmechanism for a passive compliant wrist ofmanipulators[J].Transactions of the Japan Society of Mechanical Engineers，1998，C64:2116-2 123.

[5]Pfreundschun GH，Khmer V，ThomasGS.Designandcontrolofa3 DOF in-parallel actuated manipulator[C].Proceedings，of International Conference on Robotics and Automation，1991，1659-1664.

[6]韩方元.并联机器人运动学正解新算法及工作空间本体研究[D].长春:吉林大学，2011.

[7]王进戈，范丽华，徐礼钜.3-RPS并联平台机构的位置正解与奇异构形分析的数值-符号解[J].机械设计，2005，22（5）:15-19.

[8]李树军，王 阴，王晓光.3-RPS并联机器人机构位置正解的杆长逼近法[J].东北大学学报:自然科学版，2001，22（3）:285-287.

[9]张继有，原福永，刘大为，等.基于神经网络的并联3自由度机器人位置正解[J].计算机仿真，2004，21（10）:133-135.

[10]蔺宏伟.几何迭代法及其应用综述[J].计算机辅助设计与图形学学报，2015，27（4）:582-589.