自升式平台波浪荷载计算方法的评述

李 晔(中国船级社海工技术中心, 天津 300457)

自升式平台波浪荷载计算方法的评述

李 晔
(中国船级社海工技术中心, 天津 300457)

波浪荷载对自升式平台的整体性能和作业能力有着明显的影响，对自升式平台所受波浪荷载进行合理分析可更加准确地评估平台的整体性能，进而提高平台的作业能力和作业效率。对此,通过比较ISO 19901-1,ISO 19905-1和SNAME中关于环境荷载系数的确定方法，给出合理、优化的选择环境荷载系数的方法，为平台性能评估中环境荷载的计算提供一定的参考。

自升式平台;环境荷载;波浪运动系数;整体性能

海洋自升式平台结构复杂、体积庞大、造价昂贵；同时，其所处的海洋环境十分复杂和恶劣，承受着风、海浪、海流、海冰和潮汐等多种随时间和空间变化的环境载荷的影响。环境荷载的大小对自升式平台的作业水深、桩靴能力、锁紧能力和压载能力等均有明显影响，对平台环境荷载的大小进行准确计算可有效评估平台的作业能力和整体性能，避免平台结构的冗余和浪费，同时保证平台在作业条件和抗风暴条件下的安全性。

在SNAME T&R 5-5A公告[1]被收入到ISO 19905-1[2]的过程中，海洋环境荷载的计算方法发生了一些变化。这里就波浪运动系数对波浪荷载的影响进行叙述，并对所计算的海洋环境荷载进行对比;同时,结合实际算例阐述该系数的变化对平台波浪荷载计算结果的影响。

1 波浪运动系数

通常短峰波产生的波浪荷载会小于按等效的长峰规则波计算得到的波浪荷载，而实际海况中通常都是短峰波，因此在ISO 19905生效前对如何合理有效地评估真实的波浪荷载进行大量研究。最终,ISO 19905规定通过采用合适的相关系数(即波浪运动系数)来提高波浪荷载的精确度。对于自升式平台而言，这些系数主要与平台的桩腿间距、波高、波长、波周期和水深有关，由此可得到比单桩近似理论更准确的平台桩腿波浪荷载。

SNAME通过采用合适的高阶波浪理论(如斯托克斯5阶或合适的流函数)和水动力系数(如拖曳力系数Cd1.0)来确定典型粗糙构件上的准静态波浪荷载。考虑短峰波浪海域的波浪传播效应，SNAME的推荐做法是在计算确定性规则波的波浪力时，采用波浪运动系数0.86获得真实的波浪荷载。采用该系数不仅考虑波浪的传递，而且可通过修改水动力系数考虑确定性规则波的传递，同时保证其具有足够的保守性。SNAME还建议通过降低波高来考虑波浪运动系数的作用,这主要是因为20世纪90年代初期SNAME刚刚被采用，很多计算软件都不支持输入波浪运动系数。采用SNAME推荐的方法得到的波浪荷载与波高不折减、构件拖曳力系数为0.65～0.70得到的结果较接近。

在ISO 19901-1[3]中，用波浪运动系数φ反映波浪的传递，该系数与平台所处纬度有关(见图1)，主要用于计算单桩结构上的波浪荷载。自升式平台均为多腿结构，且桩腿之间具有明显的间隔，这种间隔对计算作用于平台的波浪荷载是有利的。2000年，IADC自升式平台委员会(IJUC)赞助了一个科研项目来研究准确计算热带风暴条件和温带条件下自升式平台波浪荷载的方法，研究成果[4]与SNAME之前的结果存在一定偏差。随后，该项工作发展成了由IADC和SHELL共同赞助的一个长期科研项目，用以研究更多类型的自升式平台在更多环境条件下的环境荷载。目前的研究结果[5]表明:在热带风暴海域，环境荷载比之前理论上的计算值最多能减小35%；对于其他区域，最多能减小20%。

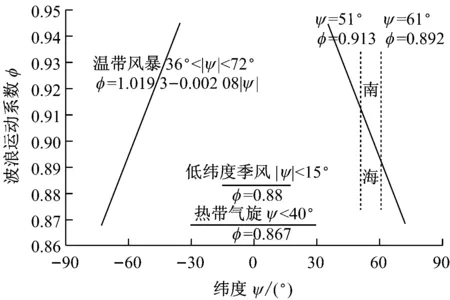
图1 波浪运动系数与平台所处纬度的关系

ISO 19905-1采用的是HOYLE提出的推荐做法，采用波浪运动系数,考虑平台的结构特征、环境条件等各种不同的影响因素，并用一个复杂公式计算该系数κ。

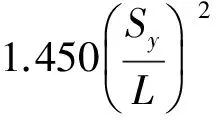
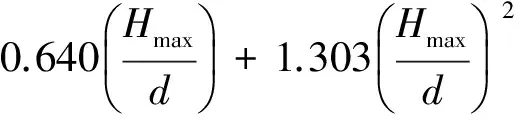
(1)

式(1)中：φ为与纬度相关的波浪运动系数；Sy为最小的桩腿间距；L为按规则波理论计算的水深、最大波高和相应周期所对应的波长；Hmax为最大波高；d为水深。

在某些特殊条件下，由式(1)得到的κ值会过于保守，因此ISO 19905-1要求κ值不能超过φ值。为满足该要求，对式(1)中的参数作以下限制。

0.08≤Sy/L≤0.43

(2)

0.14≤d/L≤0.76

(3)

0.07≤Hmax/d≤0.58

(4)

研究表明:短峰波浪海域采用ISO 19905-1中的波浪运动系数得到的环境荷载比采用SNAME的波高折减系数得到的环境荷载更逼近设计海况。

2 波浪荷载计算方法

目前，对于类似自升式平台的海洋结构，由于波长与其直径的比值(L/D)较大(>5)，因此其所受的波浪荷载均采用莫里森(Morison)方程进行求解。

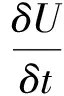
(5)

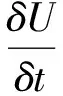
按等效长峰波计算的波浪力小于短峰波产生的实际波浪荷载，因此需在所求波浪荷载的基础上乘以波浪运动系数以提高平台结构所受波浪荷载的精确度。ISO 19901-1，ISO 19905-1和SNAME对通过式(5)计算的波浪荷载所做的修正为

ISO 19901-1:F1=F×φ

ISO 19905-1:F2=F×κ

SNAME:F3=F(h′),即采用折减后的波高计算波浪力。

3 平台波浪荷载实例计算

实例中的平台为三腿自升式钻井平台，拟在东海进行作业。该区域的地理纬度为32°N，平台桩腿间距为35.05 m，作业区水深为61 m，波高为17.37 m。周期为13.56 s，波长为268.68 m。

由图1可得φ=0.867，平台的参数(见表1)满足式(2)～式(4)中的限制。由ISO 19905-1中系数κ的计算式可得波浪运动系数为0.783。

表1 钻井平台参数

对于确定性规则波的波浪力的计算，SNAME采用的是折减后的波高Hdet。Hdet与有效波高Hs的关系为Hdet=1.60Hs，有效波高与最大波高的关系为Hmax=1.75Hs。因此，SNAME中计算波浪力采用的波高为Hdet=Hmax(1.60/1.75)=15.88 m。

按SNAME和ISO 19901-1计算得到的波浪荷载对比见表2，按ISO 19901-1和ISO 19905-1计算得到的波浪荷载对比见表3。

对比表2和3可发现:采用SNAME方法计算得到的波浪荷载与采用ISO 19901-1的波浪传递系数得到的波浪荷载相差6.5%左右，计算结果比较一致;ISO 19905-1的波浪传递系数κ考虑了平台自身的结构特征，采用该系数得到的波浪荷载比采用ISO 19901-1的系数得到的波浪荷载小18%，该结果也与之前的研究结果一致。这说明平台的结构形式(尤其是科学合理的平台桩腿间距)可极大地改善平台所受的波浪荷载。考虑到移动平台作业区域的不确定性，其作业的地理位置、作业水深及所受波浪的波高与波长均具有明显的不确定性，从而给平台确定合理高效的桩腿间距带来较大的困难。在实际设计过程中，根据平台预计的高重现率作业区域的环境条件确定合适的桩腿间距，可有效降低平台所受的波浪荷载、提高平台的作业寿命。

表2 按SNAME和ISO 19901-1计算得到的波浪荷载对比

表3 按ISO 19901-1和ISO 19905-1计算得到的波浪荷载对比

只要满足式(1)～式(3)的要求，那么计算所得的ISO 19905-1推荐的系数κ都小于ISO 19901-1推荐的系数。因此,按照ISO 19905-1计算得到的波浪荷载小于按照ISO 19901-1计算得到的波浪荷载;同时，计算得到的波浪荷载与系数之间是二次方关系。表4～表8给出了系数κ随不同变量的变化情况。

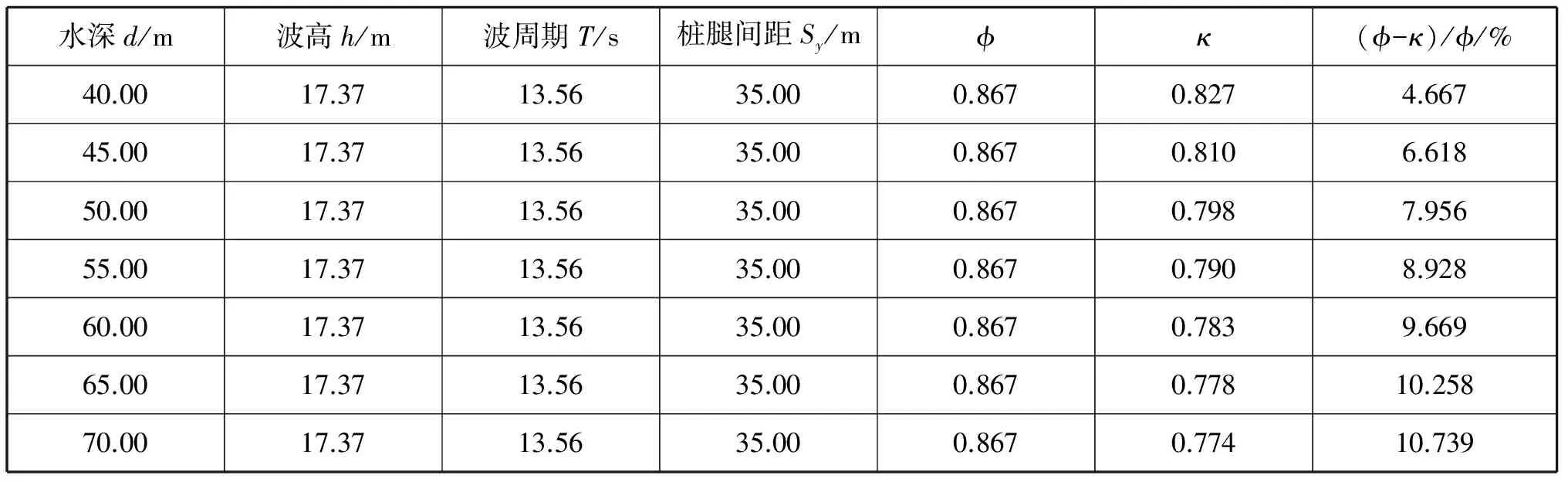
表4 系数κ随水深的变化情况

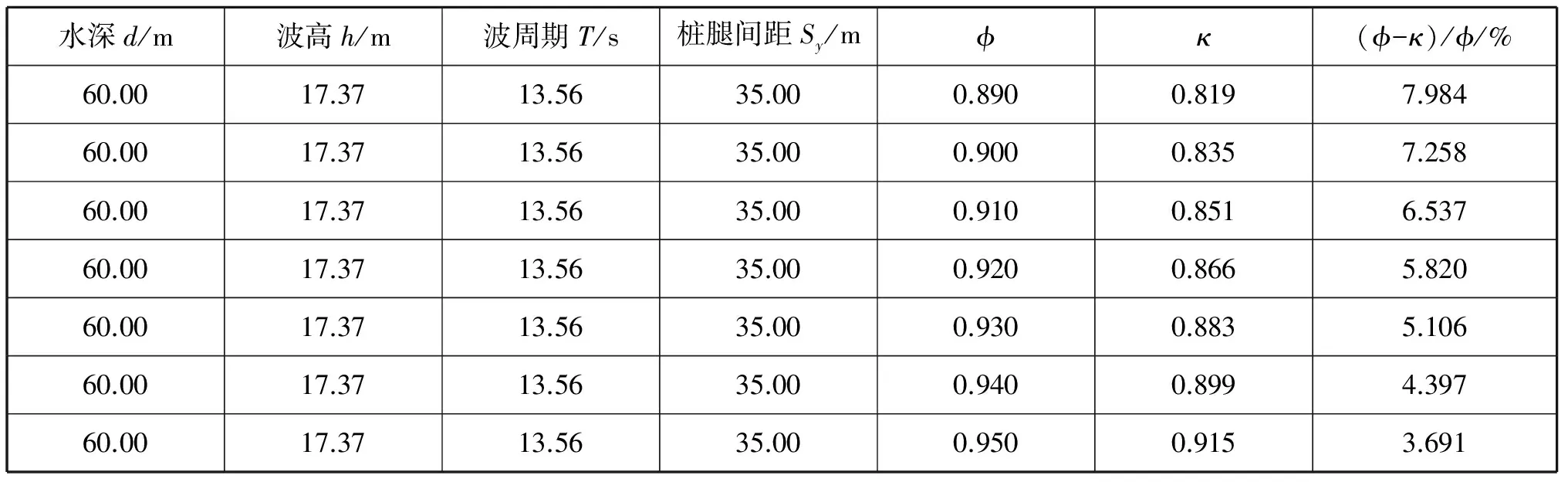
表8 系数κ随φ的变化情况

通过比较发现:在其他条件不变的情况下，水深和系数φ的变化对κ的影响最为显著，桩腿间距的影响较明显，而波高和波周期的影响较微弱。即平台所处的地理位置、水深及平台自身的桩腿间距会对环境荷载的大小产生重要的影响，因此在设计过程中,需对这些因素进行重点关注和综合比较，以提高平台的适应能力。

4 结束语

通过比较运用SNAME，ISO 19901-1和ISO 19905-1方法计算得到的波浪荷载及不同变量对ISO 19905-1波浪传递系数的影响，得到以下结论。

1) ISO 19905-1推荐的波浪传递系数κ在ISO 19901-1推荐系数的基础上考虑了波浪参数、水深和平台腿间距的影响，其中地理位置和水深对系数κ的影响最为显著。

2) 运用ISO 19905-1推荐的方法得到的环境荷载要小于运用SNAME和ISO 19901推荐的方法得到的结果，且能更好地与目前的研究结果相吻合。采用该方法指导设计,可让平台设计更加经济。

3) 对于移动平台，要综合考虑平台作业区域多变的特点，重点依据平台预计的高重现率作业区域的地理位置和环境条件确定合适的平台结构形式。

[1] SNAME.SNAME Technical & Research Bulletin 5-5A[S].2008.

[2] International Organization for Standardization. ISO 19905-1. Petroleum and Natural Gas Industries-Site-Specific Assessment of Mobile Offshore Units-Par 1: Jack-ups[S]. 2012.

[3] International Organization for Standardization. ISO 19901-1. Petroleum and Natural Gas Industries-Site-Specific Assessment of Offshore Structures-Par 1: Metocean Design and Operating Conditions[S]. 2012.

[4] SMITH SF, HOYLE MJR, AHILAN RV,etal. The Effects of New Developments in Wave Modeling on Jack-up Loads[C]. Proceedings 20th International Conference on Offshore Mechanics and Arctic Engineering, 2001.

[5] SMITH SF, HOYLE MJR, AHILAN RV,etal. 3D Nonlinear Wave Spreading on Jackup Loading and Response and Its Impact on Current Assessment Practice[J]. Offshore Technology Conference, 2006(5):1-4.

CommentsAboutAnalysisMethodsofWaveLoadonJack-UpUnit

LIYe
(CCS Offshore Engineering Center, Tianjin 300457, China)

Wave load has significant impact on the overall performance and the work ability of a jack-up unit. Rationally selecting the analysis method of the wave load can give more accurate assessment of the overall performance of thejack-up unit and help to improve the work ability and efficiency. Because of this, through comparing the methods of determining the environmental load coefficients suggested by ISO 19901-1, ISO 19905-1 and SNMAE, proposes the suitable method for determining environmental load parameters.

jack-up rig； environmental load； wave load coefficient； overall performance

2015-05-17

李 晔(1975—)，男，辽宁开原人，高级工程师，硕士，从事海上设施图纸审查、规范科研编制和海工技术研发工作研究。E-mail：liye@ccs.org.cn

1000-4653(2015)03-0079-04

P751;U674.38+1

A