基于贝叶斯方法的历史建筑砌体抗压强度推定

彭 斌，汪澜涯，李 翔，付想平

（1.上海理工大学 环境与建筑学院，上海 200093；2.同济大学 建筑工程系，上海 200092）

砌体材料在中国现存历史建筑中被大量使用，砌体材料的抗压强度（以下简称强度）是衡量这些历史建筑安全性的重要指标.但是，受建筑现状和现场条件限制，可获得的砌体强度实测样本非常有限，且量测误差明显；同时，历史建筑中砌体材料的生产工艺与现代不同，在长期使用中已受诸多因素影响，利用现行规范推定其强度，存在模型误差.因此，对历史建筑砌体强度的合理推定比较困难［1］.首先，采用少数离散样本的统计特征值进行估计，明显违背大数定律，如果样本序列过于离散，不得不舍弃部分样本，从而进一步减少了实测信息量.其次，对于历史建筑中同一检测单元的砌体强度，既可由现场原位测试来推定（直接法），也可在测得块体和砂浆的强度后用模型来推定（间接法）［2］，2 种方法推定的强度值差异明显.

在影响因素众多、量测误差明显和实测信息量不足时，合理利用可靠的先验信息，对于强度的推定非常重要.贝叶斯方法是利用先验信息的有效方法［3］.在处理既有结构材料参数的主观不确定性时，采用该方法能够以原设计中的先验信息修正实测信息量的不足［4］.在推定结构剩余承载力［5］或砌体结构的节点刚度、材料弹性模量时［6］，采用该方法可赋予先验信息和实测信息合理的权重，避免先验信息的作用被低估或放大.

为合理推定历史建筑中砌体强度，本文先建立砖强度和砂浆强度的概率密度函数（probability density function，PDF），并据此建立砌体强度推定的似然函数；再基于贝叶斯方法，合并直接法和间接法的实测信息，在推定砌体强度的同时，定量描述推定结果的不确定性.

1 贝叶斯方法及其数值实现

在参数分布的总体模型估计和先验概率密度模型的基础上，结合新增实测样本，按如下贝叶斯公式，更新待定参数的先验概率密度模型［7］：

式中：θ为待定参数；D 为新增实测样本；P（θ｜D）是θ的后验概率密度函数；P（D｜θ）和L（θ）是似然函数，表示在θ已知的条件下获得新增实测样本D 的概率；P（θ）为θ的先验概率密度函数，可根据之前的实测数据或其他先验信息（包括经验判断）来确定；P（D）为获得该组新增实测样本D 的概率密度函数；k为正则化因子，k＝1／P（D）；Q（θ）是似然函数与先验概率密度函数的积.可以证明，无论θ为何种分布，用P（θ｜D）对其进行估计的结果，与所有的已知实测数据相比，具有最小的均方误差（mean square error，MSE）；当θ严格服从正态分布时，贝叶斯方法与极大似然估计法或最小二乘估计法等效.

由于正则化因子k难以确定，很难用式（1）直接得到P（θ｜D）的解析表达式.此时可用马尓科夫蒙特卡洛（Markov Chain Monte Carlo，MCMC）方法，通过抽样重构P（θ｜D）.Metropolis－Hasting（MH）抽样方法是有效的MCMC 方法之一，其过程为［7］：

（1）随机选择参数样本值ξ.

（2）按式（2）计算比值ri：

式中：θi是第i 个样本；Q（ξ），Q（θi）是式（1）中的似然函数与先验概率密度函数的乘积；P＊（θi｜ξ），P＊（ξ｜θi）是随机选取的建议概率密度函数.

（3）从均匀分布（0，1）中随机抽样1个值αi.

（4）如果ri＞αi，则接受ξ，令θi＋1＝ξ；否则拒绝ξ，令θi＋1＝θi.返回第（2）步.

MH 方法认为，当ξ被接受的潜在可能性P＊（ξ｜θi）较大时，应该降低接受其作为样本的概率（即降低ri），以免该值的影响被过分放大.这样可以使抽样范围较快遍布样本空间，获得P（θ｜D）的全面信息［7］.为降低MH 方法得到的相邻样本间的相关性，本文抽样时放弃前200个抽样值，并根据样本序列的自相关函数，放弃显著相关的样本.

2 历史建筑砌体强度的概率模型

GB 50153—2008《工程结构可靠性设计统一标准》明确规定材料强度宜采用正态分布模型或对数正态分布模型，GB／T 50315—2011《砌体工程现场检测技术标准》给出了根据实测样本的统计特征值推定砖强度和砂浆强度的方法.但由于历史建筑砌体强度受众多因素影响，在独立测试时，其样本值通常十分离散，且其分布形态也与正态分布相去甚远，导致总体信息相当有限.此时若仍采用样本统计特征值代表总体，不符合大数定律，存在明显的偏差.因此，本文把对数正态分布和样本统计特征值仅作为先验信息的一种，而不作为直接推定的依据.另外，由于历史建筑中砖和砂浆的生产工艺、砌筑方式等与现行技术标准不符，因此将无主观信息的区间均匀分布作为另一种先验信息.

对于历史建筑，直接法或间接法获得的砌体强度样本数量均有限，且现场量测误差较大，同时间接法所用的强度计算模型并不完善.这使2种方法的推定值有明显差异.为增加砌体强度推定结果中的实测信息量，减小推定结果的不确定性，下文通过贝叶斯方法来合并直接法和间接法检测的信息，并估计强度计算模型误差的影响.

3 历史建筑砌体材料抗压强度的似然函数

现行GB 50003—2011《砌体结构设计规范》中采用以下模型来间接确定砌体强度：

式中：fm为砌体强度平均值；f1为块体强度的等级值；f2为砂浆强度的平均值；α为与块体高度有关的参数；k1为反映块体种类的参数；k2为采用低强度等级砂浆时的修正系数.

中国超过3 000组的试验结果表明，式（3）反映了砌体强度的主要规律［8］.但砌体强度还受到块体和砂浆弹性模量、块体的吸水程度和灰缝的饱满程度等诸多因素的影响，这些在式（3）中均未反映，因此用式（3）推定砌体强度时存在模型误差.

为构造砌体强度平均值fm的似然函数，对式（3）两边取对数，得到：

式中：γ为模型误差.

在测试过程无系统误差时，γ 服从均值为0 的正态分布［7］.参照GB 50153—2008 标准，取f1，f2为对数正态分布.由式（5）可知Fm服从正态分布，且：

式中：μFm，μF1，μF2分别为Fm，F1，F2的均值；，分别为Fm，F1，F2的方差.

当通过直接法获取砌体强度的实测数据后，可建立如下似然函数：

式中：n 为原位测试的次数；Fm，i为第i 次原位 测试的值.将式（6）代入式（7），可以得到：

基于贝叶斯方法，可合并直接法实测信息Fm，i和间接法实测信息，并结合先验概率密度模型来推定历史建筑砌体强度.

4 历史建筑砌体强度的检测

4.1 烧结黏土砖强度f1的检测

某历史建筑中的承重墙体采用烧结黏土砖砌筑.通过现场回弹测试和取样进行抗压强度试验来获得砖强度的样本.

现场回弹测试时，将整幢建筑的承重墙体划分为1个检测单元，在该检测单元中选取4个典型部位作为测区，在每个测区内严格按照GB／T 50315—2011标准进行回弹测试并评定强度等级.另外，切割测区中的灰缝砂浆将单块砖完整取出，共获取6个抗压强度试件，按照GB／T 5101—2003《烧结普通砖》进行抗压强度试验.评定和试验结果见表1.

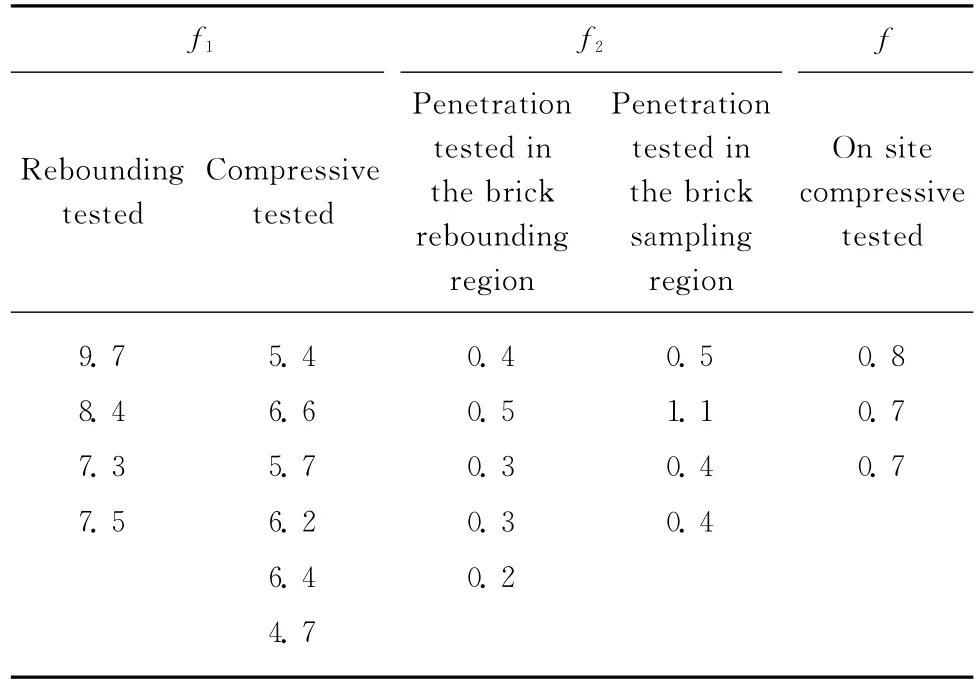
表1 抗压强度样本Table 1 Samples of compressive strength N／mm2

表1中f1的测试数据反应了砖强度的不确定性.受现场条件的限制，无法获取更多的样本，而可获取的有限强度样本值之间差异显著，因此样本的统计特征值不能代表检测单元的强度.

基于贝叶斯方法推定砖强度时，采用回弹测试的结果建立砖强度的先验概率密度模型，用抗压强度试验结果来更新砖强度的先验概率密度模型.

4.2 砂浆强度f2的检测

该历史建筑中的承重墙体采用的是石灰黏土砂浆.根据GB／T 50315—2011标准，将整幢建筑的承重墙体作为1个检测单元，凿开粉刷层后，采用贯入法测定灰缝砂浆的强度.

在砖块回弹测试的部位确定5 个测区，获得5个换算强度（即强度平均值）样本，结果如表1所示.根据砂浆强度等级的确定方法，可建立砂浆强度的先验概率密度模型.

在砖块取样的部位，获得4个换算强度样本，结果见表1.这4个样本值用于更新砂浆强度的先验概率密度模型.

4.3 砌体强度f 的现场检测

参照GB／T 50315—2011 标准，在砖和砂浆强度测区中选择3个典型部位，将承重墙体开槽后进行原位轴压法测试，其结果见表1.

5 基于贝叶斯方法的砌体强度推定

5.1 强度的后验概率模型

对于砖强度，分别采用对数正态分布和均匀分布作为先验概率密度模型，再采用MH 方法获得后验概率密度模型.对数正态分布先验模型中，根据表1中的砖强度，均值取为8.2 N／mm2，方差取为0.90；均匀分布先验概率密度模型中，先由表1中砖强度所有数据的最大值和最小值来确定区间长度，再乘以2得到上下界［2.2，12.2］.砖强度的后验概率密度模型如图1所示，其中p 为概率密度.由图1可见，由于变异系数δ很小，模型偏度不明显.

图1 砖强度的后验概率密度模型Fig.1 Posterior PDFs for compressive strength of brick

采用同样的方法获取砂浆强度的后验概率密度模型，如图2所示.其对数正态分布先验概率密度模型中，均值取表1中砂浆强度前5个测区的样本均值，即0.3N／mm2，方差取为0.01；均匀分布先验概率密度模型中，先由表1中砂浆强度所有数据的最大值和最小值来确定区间长度，再乘以2，并考虑强度值非负，得到上下界［0，1.55］.

图2 砂浆强度的后验概率密度模型Fig.2 Posterior PDFs for compressive strength of mortar

在砖强度的后验概率密度模型中，取变异系数较小的模型（图1（a））确定μF1，分别 为3.6，0.001；在砂浆强度的后验概率密度模型中，取变异系数较小的模型（图2（a））确定μF2，分别为－0.7，0.039；再合并表1中砌体强度的数据来更新似然函数式（8）.分别采用［0，0.01］，［0，0.05］和［0，0.1］内的无信息均匀分布先验概率密度模型，并采用MH 方法进行抽样，获得砌体强度推定误差的后验概率密度模型，如图3所示.由图3可见，基于不同先验概率密度模型的后验概率密度模型均值和变异系数接近，即先验概率密度模型的差异对的不确定性影响较小.

5.2 砌体强度推定结果

将图1～3中后验概率密度模型的统计特征值分别代入式（6a）和式（6b），可确定砌体抗压强度的对数Fm服从正态分布N（－0.27，0.25）.再根据对数正态分布特征，可推定fm＝0.9N／mm2，fm的不确定性程度可由图3定量给出.

根据表1，采用间接法时，砌体强度可推定为0.6N／mm2；采用直接法时，砌体强度可推定为0.7N／mm2.直接法和间接法推定结果之间有差异，由模型误差、量测误差等导致的不确定性难以衡量；并且间接法中的砂浆强度和直接法中的砌体强度均由相应样本中的最小值确定，从而丢失了其他样本的信息.而基于贝叶斯方法的推定结果利用了所有实测样本和可靠的先验判断，其信息量比单独通过间接法或直接法获得的推定值更为丰富.

图3 的后验概率密度模型Fig.3 Posterior PDFs forσ2γ

5.3 贝叶斯方法推定结果的性质

基于贝叶斯方法的历史建筑砌体强度推定过程不舍弃实测样本，保证了推定结果中实测信息的完整性，满足大数定律的要求.推定结果结合了先验信息和实测信息，并自动对这2类信息赋予合理的权重.如果实测信息的不确定性较小，其将获得较大的权重，此时先验概率密度模型的差异将不会显著影响后验概率密度模型的统计参数（见图1）.如果实测信息较为离散，则由不同先验概率密度模型所得后验概率密度模型的均值差异较明显，且变异系数都很大（见图2），此时抽样过程更依赖于先验信息.这说明在现场实测信息不足的条件下，可靠的先验信息对于强度的估计具有重要的意义.此时为避免主观性的影响，应采用不同的先验概率密度模型进行MH 抽样，然后对相应的后验概率密度模型进行对比分析.

基于贝叶斯方法的强度推定结果具有可扩展性，适用于砌体强度的长期观测.当获得新的实测数据时，可将已有的后验概率密度模型作为先验信息，重新启动推定过程进一步更新.如果砌体强度稳定，推定结果的不确定性将随实测信息的累积而不断减小；如果砌体强度受外部环境或其他因素影响而发生改变，则后续的实测数据将更新已有的判断.

强度的后验概率模型可定量表示推定结果的不确定性，对于决策非常有利.由图2中后验概率密度模型的统计特征，可分别推定砂浆强度值为0.5N／mm2（正态先验）和0.6N／mm2（均匀先验）；根据后验概率密度模型的变异系数，可判定0.5N／mm2具有较小的不确定性.对比图1，2中后验概率密度模型的变异系数可知，实测的砖强度比砂浆强度更可靠，这符合砌体强度现场检测时砂浆风化程度较高的一般规律.

基于贝叶斯方法的强度推定结果含义丰富.首先，模型误差的方差的后验概率密度模型可作为决策的定量依据的最优值可通过逐次搜索确定.如图3所示，先验概率密度模型为均匀分布时，其下界为0，逐次变化上界，可分别获得的后验概率密度模型；当后验概率密度模型的统计参数趋于稳定时，可将该模型的均值作为的估计值.其次，砌体强度对各因素的敏感性可由各因素的后验概率密度模型来定量描述.由式（6b）以及图1，2中后验概率密度模型的统计特征可知，砂浆强度的不确定性对砌体强度推定结果的不确定性影响较大.这与当前工程实践中的情况一致，可作为工程问题的理论解释.最后，对于历史建筑，现场条件对直接法限制较大，此时可通过增加间接法的实测样本数来降低强度推定结果的不确定性，式（8）为此提供了理论依据.

6 结论

（1）贝叶斯方法不舍弃实测样本，保证了推定结果中实测信息的完整性.通过累积实测信息可以不断更新推定结果，以经济、有效的方式实现砌体强度的长期观测.

（2）贝叶斯方法定量给出了推定结果的不确定性及其对各影响因素的依赖程度，有利于客观分析和决策.推定结果表明，砂浆强度的不确定性对砌体强度推定结果的影响显著.

（3）贝叶斯方法可将直接法和间接法获得的砌体强度信息相结合，从而降低推定结果的不确定性.该方法从理论上说明，对于历史建筑，可通过增加间接法的实测样本数来获得更为合理的砌体强度推定结果.

［1］SYNGELLAKIS S.Heritage masonry：Materials and structures［M］.Billerica：WIT Press，2013：1－33.

［2］DG／TJ 08—804—2005 既有建筑物结构检测与评定标准［S］.DG／TJ 08—804—2005 Standard for structural inspection and assessment for existing buildings［S］.（in Chinese）

［3］BECK J L，KATAFYGIOTIS L S.Updating models and their uncertainties I：Bayesian statistical［J］.Journal of Engineering Mechanics，ASCE，1998，124（4）：455－461.

［4］姚继涛.现有结构材料强度的统计推断［J］.西安建筑科技大学学报：自然科学版，2003，35（4）：307－311.YAO Jitao.Statistical inference of material strength of existing structures［J］.Journal of Xi'an University of Architechture ＆Technology：Natural Science，2003，35（4）：307－311.（in Chinese）

［5］刘书奎，吴子燕，韩晖，等.基于物理参数贝叶斯更新的桥梁剩余强度估计研究［J］.工程力学，2011，28（8）：126－132.LIU Shukui，WU Ziyan，HAN Hui，et al.Remaining load capacity estimation of bridge structures based on the Bayesianupdated physical parameters［J］.Engineering Mechanics，2011，28（8）：126－132.（in Chinese）

［6］ATAMTURKTUR S，HEMEZ F，UNAL C.Calibration under uncertainty for finite element models of masonry［R］.Los Alamos，NM：Report LA－242，Los Alamos National Laboratory（LANL），2010.

［7］HOFF P D.A first course in Bayesian statistical methods［M］.New York：Springer Science＋Business Media，2009：67－89.

［8］唐岱新，龚绍熙，周炳章.砌体结构设计规范理解与应用［M］.2版.北京：中国建筑工业出版社，2012：21－23.TANG Daixin，GONG Shaoxi，ZHOU Bingzhang.Understanding and application of code for design of masonry structures［M］.2nd ed.Beijing：China Architecture and Building Press，2012：21－23.（in Chinese）