四足步行机动平台单腿结构设计

谭永营，王 睿

(1.装甲兵工程学院机械工程系，北京 100072;2.中国人民解放军92510 部队，524300)

足式移动方式依靠与地面之间离散的接触点实现了在复杂地形中的良好运动性能和动力性能。与轮式或者履带式移动方式相比，足式运动适应复杂地形的能力更强，这也是大型动物多为四足哺乳动物的原因。模仿四足哺乳动物而研制的四足步行机动平台在复杂环境中具有巨大的应用潜力，其已成为各国学者研究的热点。四足步行机动平台腿部的结构设计是机动平台设计过程中的核心工作之一，国内外学者对机动平台单腿结构设计进行了充分的关注。

较早的步行机动平台腿部结构多为仿照爬行动物的腿部结构，如日本的TITAN 系列四足步行机动平台［1］。但这些步行机动平台运动速度慢，能实现的步态少，单腿机械结构是其受到限制的根本原因。自从Bigdog 四足步行机动平台公布以来，腿部结构仿哺乳动物的步行机动平台不断引起人们的重视［2］。作为高性能四足步行机动平台的典型代表，Bigdog 四足步行机动平台单腿分为四个部分，配置四个主动自由度，足端装有减小腿与地面冲击的被动自由度。Bigdog之后的重型运载平台—LS3 四足步行机动平台单腿有三个主动自由度，关节运动非常灵活，整体采用主动柔顺控制，取消了足端弹簧。Bigdog 系列的最新产品Spot 四足步行机动平台单腿也有三个主动自由度，各部分协调运作的能力更强，关节的活动更加自如，非常适合在人类的生活环境中使用。

从Bigdog 系列四足步行机动平台的发展可以看出，单腿的结构对机动平台的各项性能有重要影响，进而决定了机动平台的应用领域。单腿的结构设计主要包括了单腿的自由度设置、各驱动关节的活动范围设定、各腿段的长度比例以及足端轨迹曲线等。

1 单腿的自由度设置和各关节的转角范围

通过对四足哺乳动物腿部骨骼结构的研究发现，动物腿部一般由5 个主要的部分组成，各部分之间由关节连接，单腿有5 个主动自由度。动物腿部的特殊结构和冗余自由度使其运动灵活，适应复杂地形的能力非常强。步行机动平台是模仿四足动物设计的，但是由于技术水平的限制，单腿还无法达到主动自由度大于4。因此为了减小控制的难度，降低机械结构的复杂程度，设计的机动平台单腿有3 个主动自由度，分别是:髋侧摆段关节、髋纵摆关节和膝关节，如图1所示。

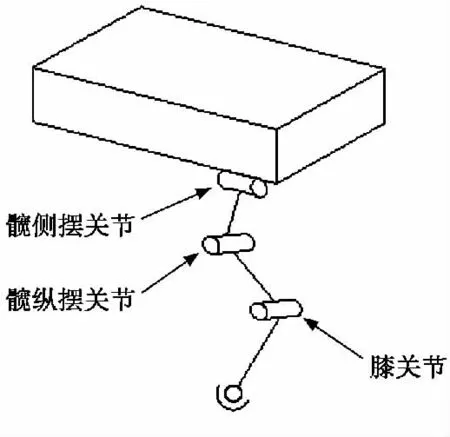
图1 单腿主动关节

步行机动平台的机体在腿部的推动下不断前进，腿部驱动关节转角范围的大小代表了机动平台足端点能达到的范围。关节转角范围越大，机动平台单腿活动范围越大，机动平台运动和抗侧向干扰的能力也就越强。但关节活动范围越大也增加了各关节段干涉的风险。通过对四足动物关节转角范围的测量来解决这个问题。Jaegger 等较准确地测量了德国牧羊犬各关节(除了髋侧摆关节)转角的变化［3］，如图2 所示。

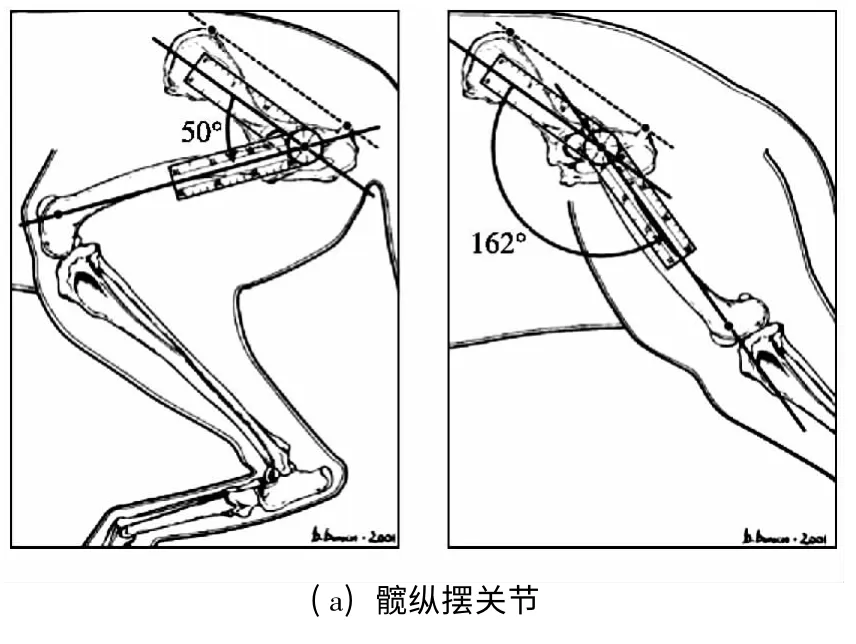
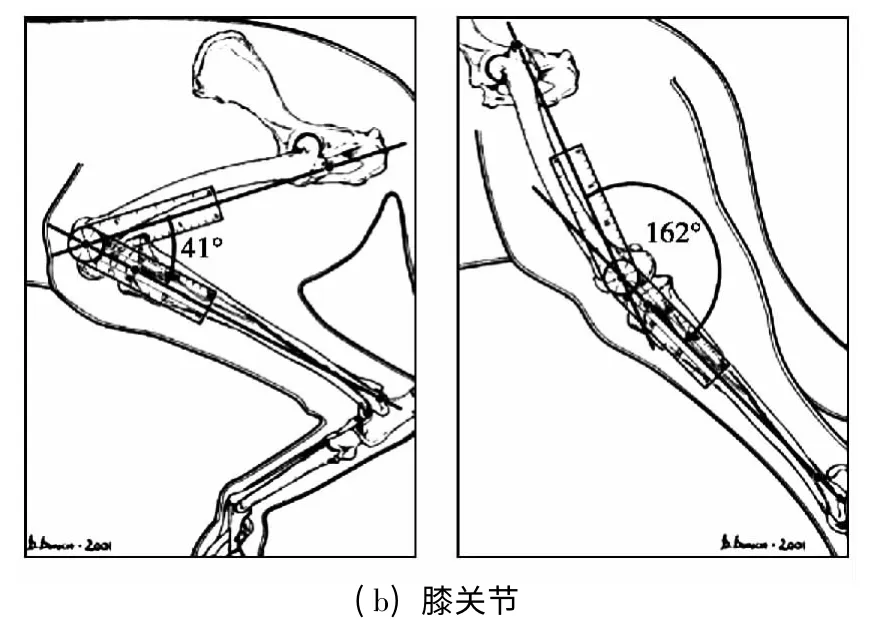
图2 德国牧羊犬关节的活动范围

由上图可以得德国牧羊犬各关节角的活动范围，如表1中所示。

表1 牧羊犬各关节角的活动范围

由表1 中数据可以得到牧羊犬关节的活动范围基本上在110°左右。在步行机动平台设计过程中，考虑到机械系统的性能还无法达到动物骨骼肌肉系统的性能，并且当各驱动关节采用相同型号的液压缸时，机动平台整体的复杂程度大大减小，因此对表中各关节转角的变化范围进行了修正，使用修正后的关节活动范围作为机动平台关节的活动范围。

2 单腿运动学分析

步行机动平台单腿的运动学分析是机动平台动力学求解和足端曲线合理规划等后续工作的基础。本文用D-H 坐标法对机动平台的单腿进行运动学分析(以右前腿为例)。首先建立各腿段的D-H 坐标系，如图3 中所示。B1-x0y0z0为右前腿坐标系，H1-x1y1z1为髋关节纵摆关节坐标系，K1-x2y2z2为髋纵摆关节坐标系，A1-x3y3z3为膝关节坐标系，F1-x4y4z4为足端坐标系。

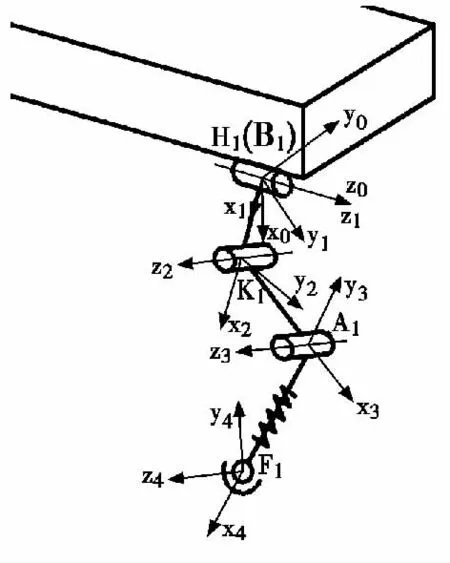
图3 步行机动平台右前腿坐标系

由D-H 坐标系的定义和各杆件的尺寸参数，可以得到D-H 法各变量的值，如表2 中所示。ai为沿xi轴方向从zi－1轴和xi轴的交点到第i 坐标系原点的距离;αi为按右手法则，绕xi轴由zi－1轴转向zi轴转过的角度;di为沿zi－1轴方向从第i－1 坐标系的原点到zi－1轴和xi轴的交点的距离;θi为按右手法则，绕zi－1轴由xi－1轴转向xi轴转过的角度。

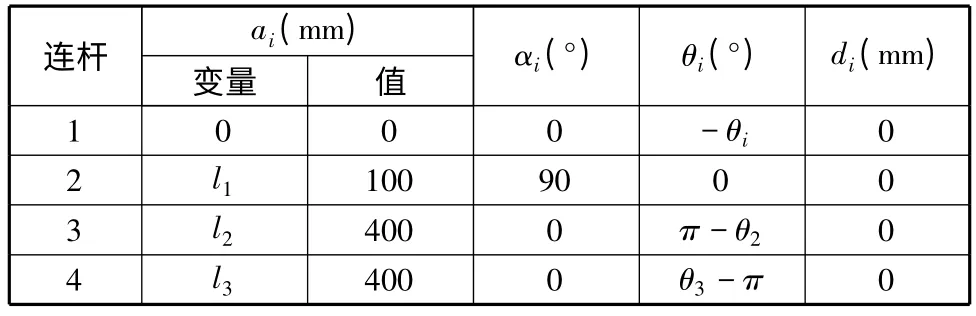
表2 D-H 方法各变量的值

所以，从右前腿坐标系到足端坐标系的各旋转变换矩阵为:

所以，设总的齐次变换矩阵为T4，并且设

代入各旋转变换矩阵进行运算得到T4中各元素为:

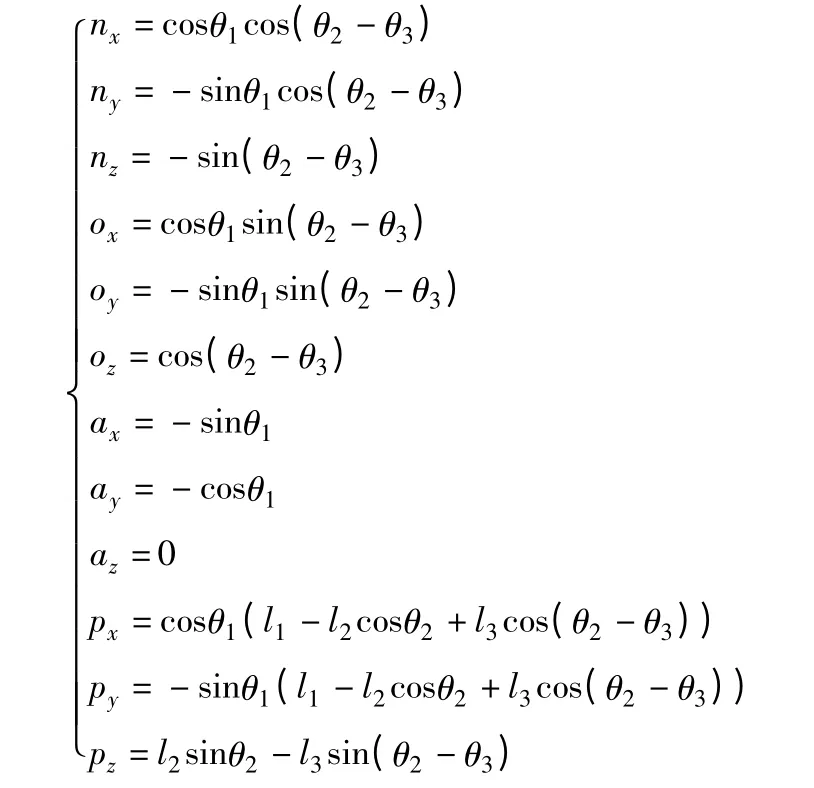
由正运动学分析，得到了足端点在单腿坐标系中的坐标和姿态。下面运用正运动学分析的结果，对各关节段的比例关系进行研究。

3 各腿段的长度比例研究

3.1 机器人足端工作空间分析

步行机动平台的足端点工作空间是其摆动腿末端参考点所能达到的空间点的范围。这个范围代表了机动平台摆动腿所能到达的位置，是机动平台结构优化设计需要考虑的重要方面。足端工作空间的求解方法有解析法、图解法或数值法等多种。利用正运动学分析的结果，在Matlab 中求解得到各主动关节角度变化时足端点的工作空间云图，然后运用图像处理方法进行足端工作空间面积的求解。求解的步骤为:

1)在各关节的变化范围内，使关节依次产生一定的转角，得到了关节角变量的组合。

2)将关节角变量带入正运动学解中，得到一组足端点的坐标值，并作出其曲线图，众多的曲线图组合形成云图。

3)按照Matlab 中图像处理的办法，得到足端空间的面积。

3.2 各腿段的长度比例研究

由于步行机动平台主要是在前后方向运动，侧向运动往往用于保证机动平台自身的稳定性，使机动平台适应复杂地形的能力更强，而两个纵摆关节段是机体前后方向运动依靠的杆件，因此仅对两个纵摆关节段的长度比例进行研究。为使研究简便同时也有代表性，假设髋关节纵摆段和小腿段的总长为1 m，两腿段的长度依次取遍0.1～0.9 m，步长为0.1 m，且L1为髋关节纵摆段长度标识，L2为小腿段的长度标识。当L1与L2取不同的比例时，利用Matlab 作出其工作空间的云图并计算面积大小，如表2 中所示。

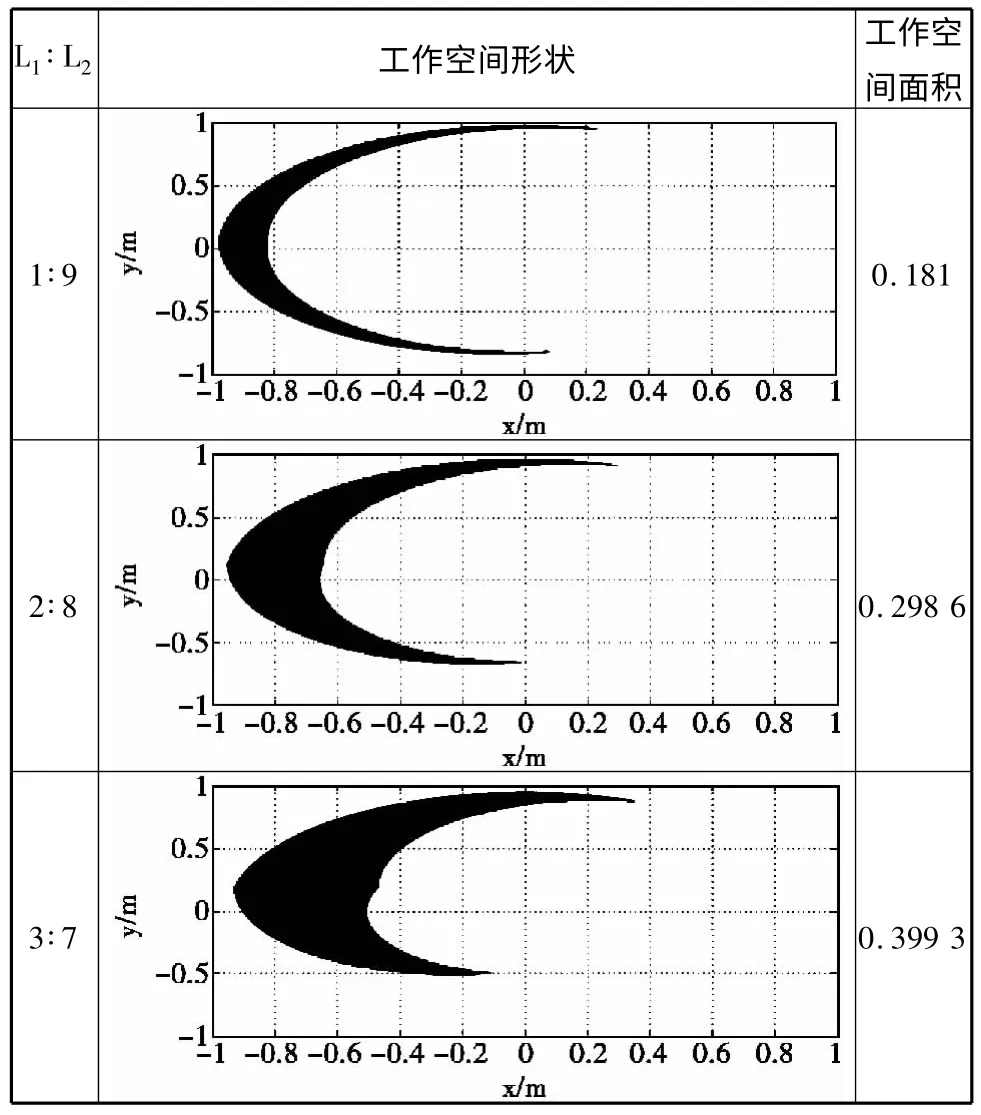
表2 杆长比例不同时的工作空间

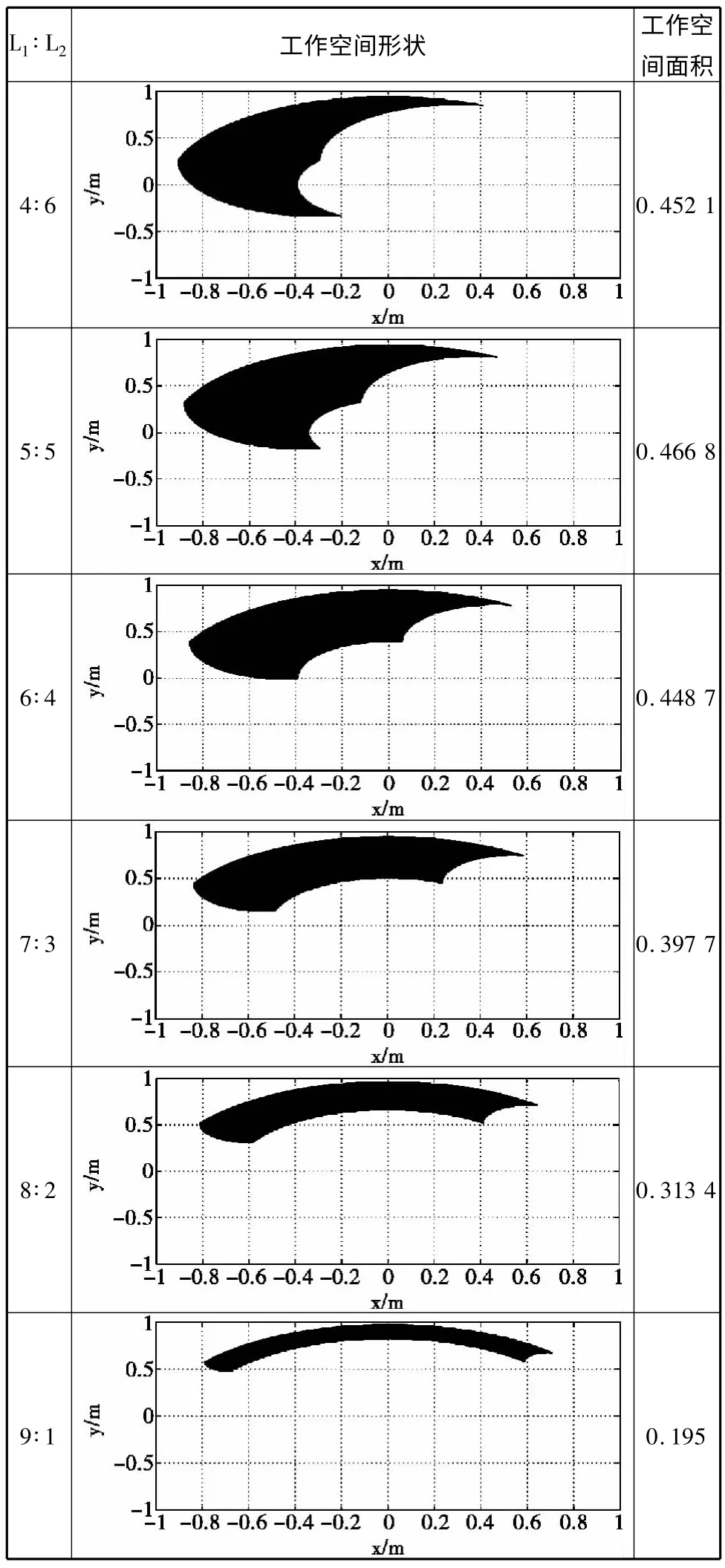
由表2 可以得到，随着L1与L2比值的增大，步行机动平台足端工作空间大小变化显著，足端点可达范围先增大后减小，所以存在使足端工作空间最大的最优比例。为方便比较，作出足端工作空间面积大小与髋纵摆段长度L1的曲线图。由图4 可更直观的得到当L1与L2相等时，足端工作空间面积最大。

图4 足端工作空间面积的变化

4 足端轨迹规划

步行机动平台足端轨迹规划是机动平台单腿设计很重要的一个方面。足端轨迹规划一般是设计步行机动平台足端点相对地面坐标系的运动规律。由于髋侧摆关节在机动平台正常行走过程中一般不发挥作用，所以在机动平台单腿平面内进行足端轨迹规划。步行机动平台通过迈腿实现其越障和前进功能，腿部足端轨迹规划主要是摆动腿足端的轨迹规划。摆动腿足端轨迹规划的好坏直接决定了机动平台的越障能力和运动能力。常用的足端轨迹有抛物线、直线段、摆线等［4］。本文采用三次B 样条曲线进行机动平台的足端轨迹规划。

4.1 三次B 样条曲线的概念

对于给定的m+n+1 空间顶点pi(i=0，1，…，m +n)，第k(K=0，1，2…n)段n 次B 样条曲线定义为［4］:

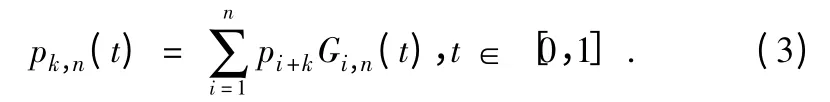
式(3)中t 为曲线的构形参数。基函数Gi，n(t)定义如下:

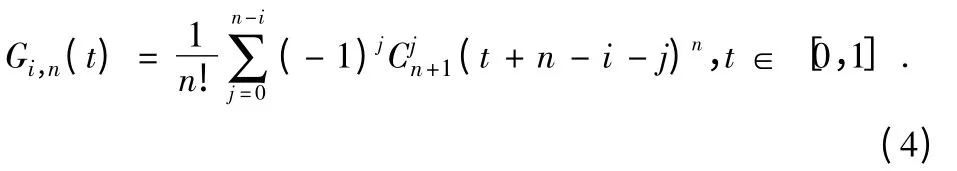
当n=3 时，由上式我们可以得到三次B 样条曲线的基函数为:

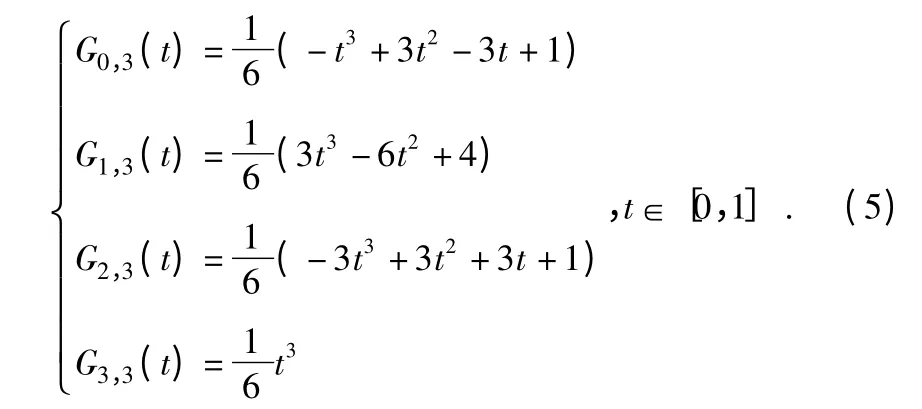
对于给定的空间顶点p0、p1、p2和p3，三次B 样条曲线的一段为:

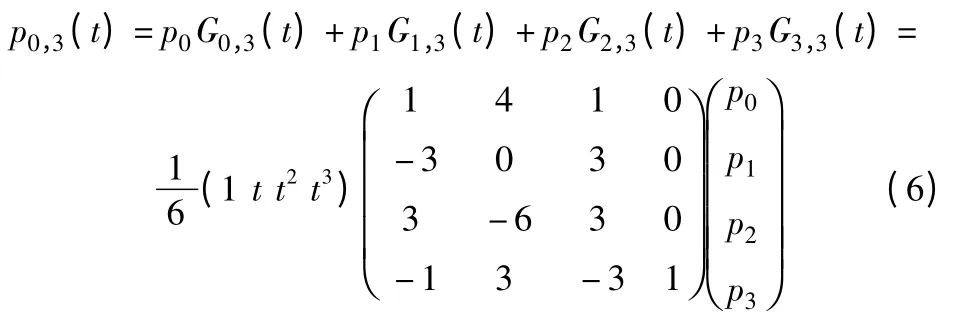
所以对于空间中给定的n 个点，三次B 样条曲线全体为:

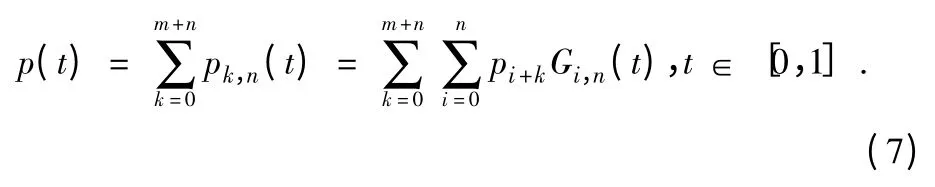
三次均匀B 样条曲线作为一种自由曲线，它自身有许多良好的特点，使它适合作为步行机动平台越障时足端轨迹曲线［5］。首先，三次均匀B 样条曲线与空间顶点的绝对位置没有关系，只与它们的相对位置有关。其次，三次均匀B 样条曲线有凸包性和保凸性。通过选取适当的空间顶点，可以使构造的足端轨迹曲线不会产生奇异点。然后，三次均匀B样条曲线具有局部修改性。改变个别的空间顶点，只会影响与这个顶点有关的构造曲线，不会对整体产生影响。

4.2 足端轨迹的规划

在平坦地面上四足步行机动平台的足端轨迹曲线一般有两个参数来描述，一个是步长s，一个是步高h。步长s 和步高h 可以较好地反映足端轨迹曲线的运动特性。一般步高h 与步长s 的比值越大，说明四足步行机动平台的跨越障碍的能力越强，但运动速度较慢。步高h 与步长s 的比值越小，说明四足步行机动平台前进特性较好，但跨越障碍的能力较差。而对于三次B 样条曲线，在步长一定的情况下，步高由起步角和落步角决定，因此引入起步角α、落步角β 和步长S 来描述三次B 样条曲线。如图5 所示，图中α 为起步角，β 为落步角，p1点为起步点，p2为落步点，M 点为起脚方向与落脚方向的交点。

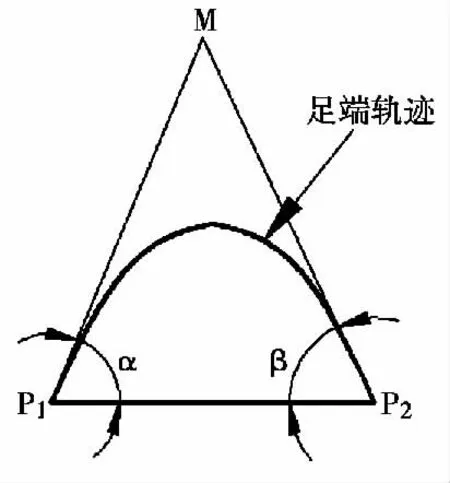
图5 起步角与落步角示意图

在此步长S 设置为400 mm，起步角和落步角均为62.5度，最大步高为220 mm。所以，可得到摆动腿的足端曲线如图6 所示。

图6 摆动腿足端轨迹曲线

5 结论

1)对四足步行机动平台单腿的自由度数进行了设定，在仿生学分析的基础上将各驱动关节的转角范围设置为40°～140°;

2)对单腿进行了运动学分析，并且在此基础上对髋纵摆关节段和大腿段长度比例不同时的足端工作空间进行了研究，得出了当两者长度相等时足端工作空间最大的结论;

3)阐述了三次B 样条曲线的概念，并在此基础上对足端轨迹曲线进行了规划。

［1］Shigeo Hirose，Kan Yoneda，Riki Furuya，et al.Dynamic and Static Fusion Control of Quadruped Walking Vehicle［J］.Workshop on Intelligent Robots and Systems，1989：199－208.

［2］Raibert MH，Benjamin Brown H，et al.On the Stability Properties of Quadruped CreepingGaits［J］.Mathematical Biosciences，1968(3) ：331－351.

［3］Claudio.HyQ-Design and Development of a Hydralically Actuated Quadruped Robot［D］.Italy：University of Genoa，2010：58－60.

［4］陈学东，孙翊，贾文川.多足步行机器人运动规划与控制［M］.武汉：华中科技大学出版社，2006.

［5］王增波，彭仁忠，宫兆刚.B 样条曲线生成原理及实现［J］.石河子大学学报(自然科学版)，2009，27(1) ：118－121.

［6］陈丹.基于遗传算法的B 样条曲线优化在机器人轨迹规划中应用［D］.武汉：武汉科技大学，2007：25－30.