某重型汽车断开式转向系统的优化设计

章菊，冯樱

（湖北汽车工业学院汽车工程学院，湖北十堰442002）

汽车转向系统的运动学分析是汽车操纵稳定性、平顺性等性能的重要内容之一，其转向性能直接影响整车的灵活性、稳定性、舒适性和经济性。转向系统的设计主要任务是保证车辆在转向过程中所有车轮都绕一个瞬时转动中心转动，做纯滚动而避免车轮侧滑，即阿克曼理论转向特性。本文中以某重型汽车断开式转向系统为研究对象，基于Adams/View 建立虚拟样机模型并进行运动学仿真分析，对比实际转向时内外轮转角关系与阿克曼转向特性的误差大小，然后利用Adams 提供的优化算法，实现参数化模型的优化设计，获得最佳杆件参数数据组合，以改善汽车转向操纵稳定性。

1 转向系统结构分析与模型的建立

1.1 转向系统结构分析

本文中分析的断开式转向系统采用横置液压缸驱动，由转向节、转向节臂、液压缸、横拉杆、转向曲柄等组成见图1。其工作原理是液压系统控制液压缸内活塞的往复运动，带动液压缸推力杆，推力杆推动转向节臂使其绕主销转动，带动同侧车轮摆动，同时，转动过程中转向节臂带动同侧横拉杆，横拉杆通过球销带动转向曲柄转动，从而推动另一侧横拉杆，使车轮实现左右摆动。

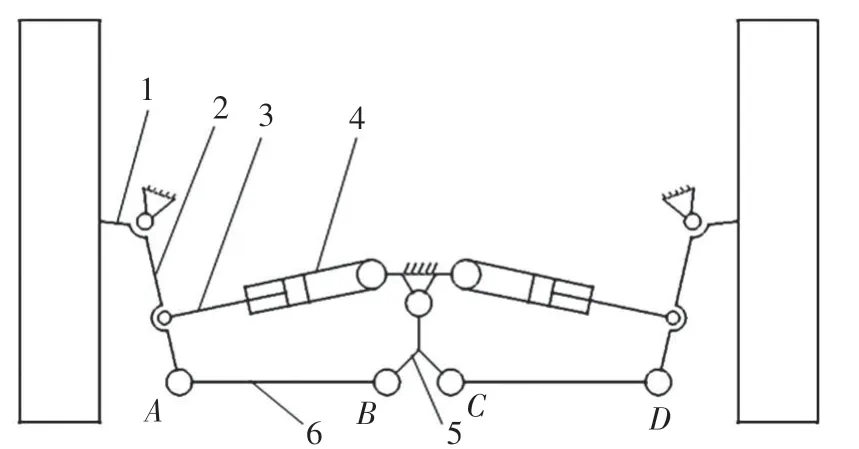
图1 断开式转向系统示意图

1.2 转向系统参数化模型的建立

通过Adams/View模块建立断开式转向系统的参数化三维模型（图2）。转向梯形机构的变化可等效为横拉杆长度的变化，在建模过程中要对重要部件的位置及尺寸进行参数化（表1），根据图1所示的结构关系，首先由初始值初步确定结构硬点的位置及构件的尺寸，然后将结构硬点的位置坐标进行参数化，左右横拉杆的长度、转向节臂及转向节臂球销长度创建为设计变量，这样设计变量随结构硬点坐标改变时，转向系统模型也会随之改变。

图2 断开式转向系运动学简化模型

表1 模型主要参数表

在参数化模型的过程中，左侧转向节臂与横拉杆之间连接处（图1点A），硬点A坐标分别设为DV_1L_X、DV_1L_Y、DV_1L_Z，右侧转向节臂与横拉杆之间连接处（图1点D），硬点D坐标分别设为DV_1R_X、DV_1R_Y、DV_1R_Z，左侧横拉杆与转向曲柄之间连接处（图1点B），硬点B坐标分别设为DV_2L_X、DV_2L_Y、DV_2L_Z，右侧横拉杆与转向曲柄之间连接处（图1点C），硬点C坐标分别设为DV_2R_X、DV_2R_Y、DV_2R_Z。

各零部件之间有相对运动，则需要施加约束（图1）：横梁施加固定约束，转向节1与转向节臂2间施加固定约束，转向节臂2与液压缸推力杆3之间为球副约束，液压缸推力杆3与液压缸体4之间施加移动副约束，转向节臂2与横拉杆6之间为球副约束，横拉杆6与转向曲柄5之间为球副约束，转向曲柄5与横梁之间通过销孔施加旋转副约束。

在液压缸推力杆与液压缸体之间的移动副上施加沿缸体方向的移动驱动MOTION_1。

2 理论转角关系

为使汽车能顺利转向，各轮胎不产生滑动，内外转向车轮之间应满足一定的运动协调关系，即满足阿克曼原理（Ackerman principle），转向轮转角关系如图3所示。

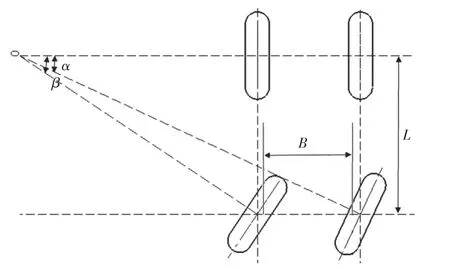
图3 内外转向车轮偏转角关系

转向时内外车轮偏转角度不相等，假设车轮为刚体，内外转向车轮转角的理论关系为

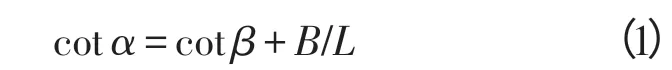
式中：α为外侧车轮偏转角；β为内侧车轮偏转角；B为两侧主销轴线与地面交点间的距离；L为整车的轴距。由此得到转向机构性能为

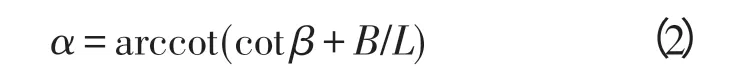
在Adams/View中输入式（2），可得到外轮转角随内轮转角变化的理论关系曲线。

3 仿真分析

分析此重型汽车断开式转向系统工作过程时，主要研究外轮转角随内轮转角偏转的变化关系。为模型输入载荷驱动MOTION_1，使模型进行运动仿真测试，仿真后得到内轮实际转角、外轮实际转角及外轮随内轮偏转的实际转角曲线，即根据虚拟模型中给定的β，可得到相对应的α 实际值（图4）。将外轮实际转角α与理论转角进行对比，由图4和图5可知，内轮转角较小时，外轮实际转角与理论值基本吻合，随着车轮转角的增大，内外轮转角差异也变大；当内轮转角β为38°时，外轮实际转角值为24.44°，与理论值27.352°相差3°，误差达到10.96%（本文中此转向系统允许的相对误差值在5%左右），误差量过大，表明该车在行驶过程中轮胎不是作纯滚动，而存在较大的滑动，严重影响该车操纵稳定性和轮胎使用情况。

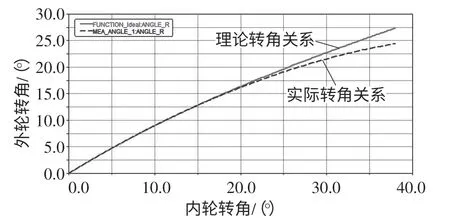
图4 转角关系曲线

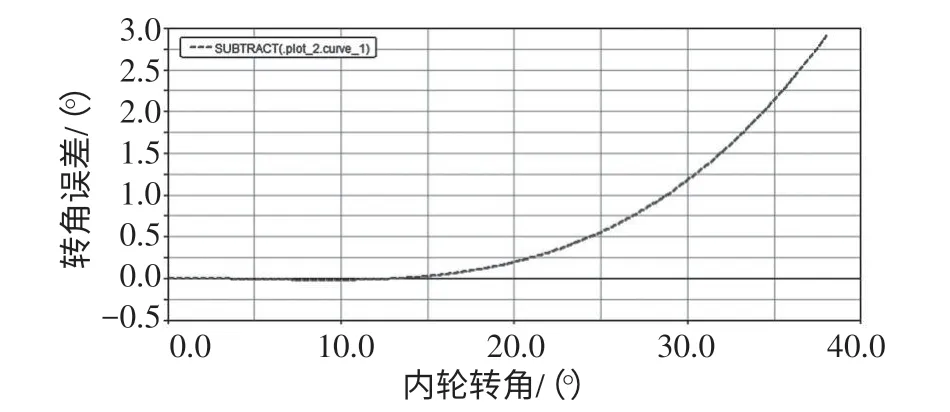
图5 外轮实际转角与理论转角误差曲线

4 优化设计

为了改善转向性能，需要对各个部件进行调整，由于转向节、主销尺寸、液压缸等会影响整车尺寸、轮距、液压动力等基本参数，且横拉杆尺寸调整在实际中比较容易实现，本文中主要考虑对横拉杆的位置及尺寸进行调整来进行优化。

利用建立好的模型，以与横拉杆相连的4个球销位置坐标为设计变量，以外轮实际转角与理论转角之差为目标函数，使目标函数达到最小值。

在优化之前，首先运用Adams软件中的Insight模块分析各个参数对目标函数的影响程度，找出对目标值影响最大的参数，灵敏度分析结果见表2。

由表2可知，DV_1R_X、DV_1R_Y、DV_1L_X、DV_2R_X、DV_2R_Y、DV_2L_X 对目标函数影响较大（灵敏度正负值表示参数对目标函数变化趋势相同或者相反），提取这8个参数设定为下一步优化设计的设计变量，运用Adams软件优化算法对此断开式转向系统进行优化，得到优化后的转角曲线关系，如图6所示。

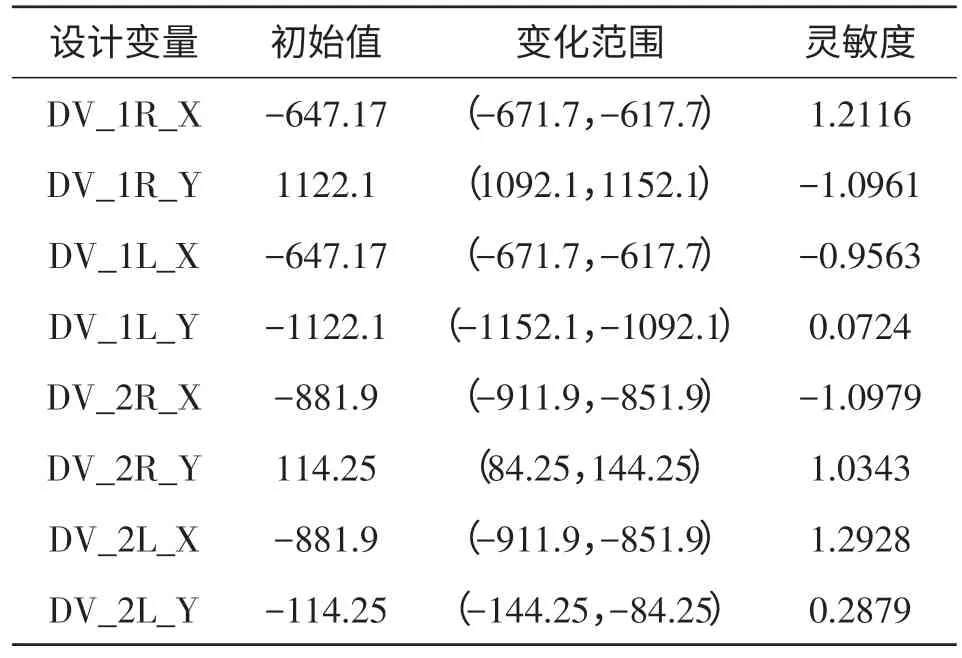
表2 参数灵敏度分析结果

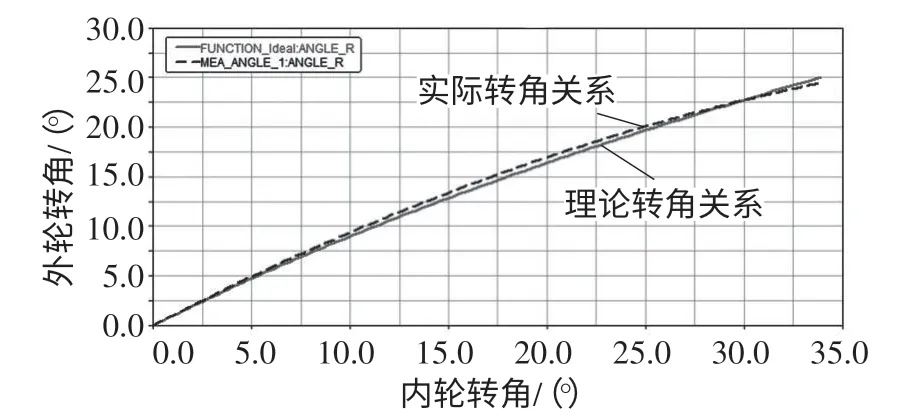
图6 优化后转角关系曲线

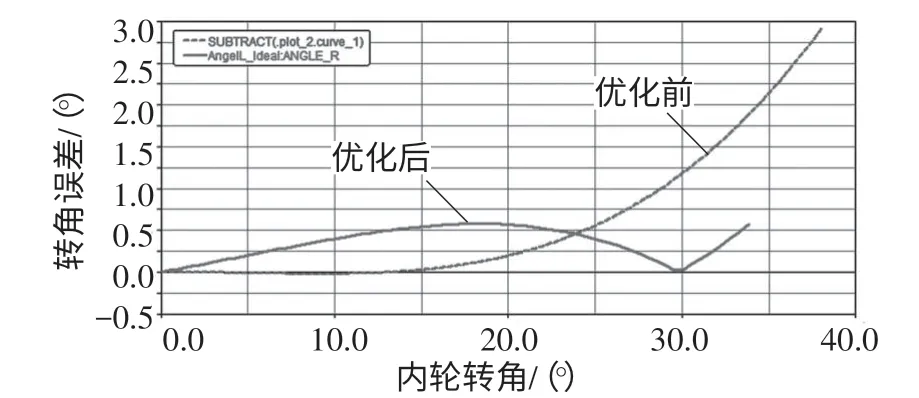
图7 优化前后误差曲线对比图

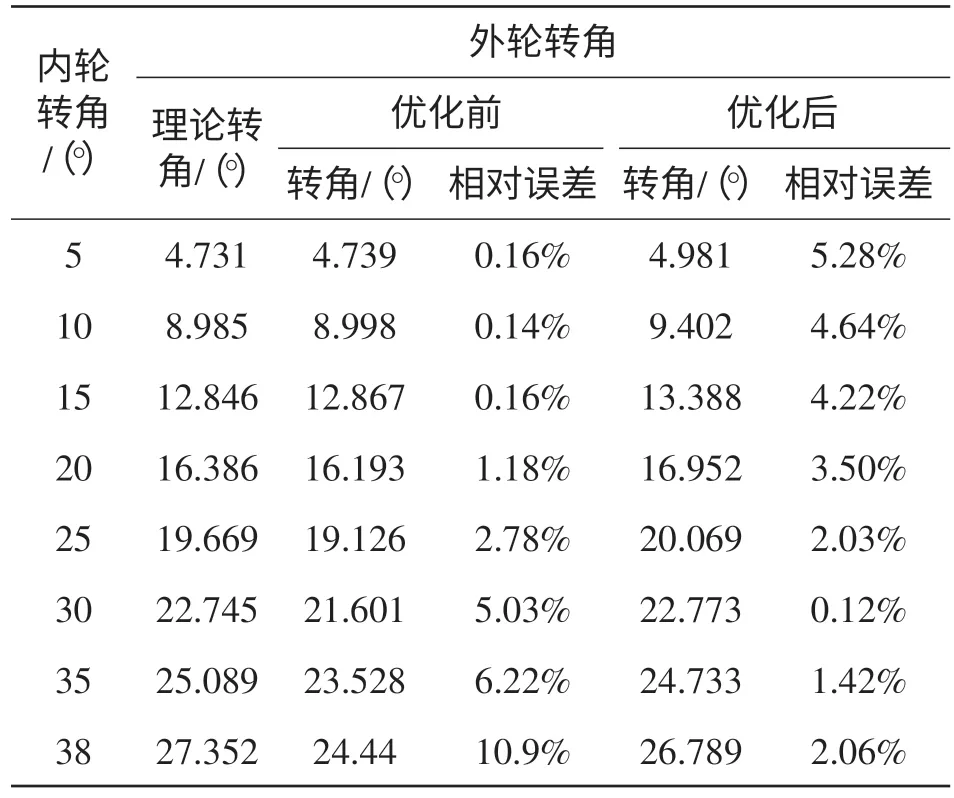
表3 优化前后转角值与误差

由图7和表3可知，优化前，开始转向时外轮实际转角与理论转角基本吻合，但随着内轮转角的增大，误差越来越大，即外轮转向偏差较大，转向不稳定；由图6和表3可知，优化后外轮实际转角曲线与理论转角曲线走向趋势基本一致，且整个转向过程实际转角与理论转角的误差均不大，当内轮转角为38°时，外轮实际转角为26.7885°，理论转角为27.352°，相差0.5634°,误差降为2.06%，在误差允许范围内。模型外轮实际转角值与理论值相当接近，优化结果比较理想。优化后从Adams软件Design Evaluation中得到设计变量的最优值（表4）。

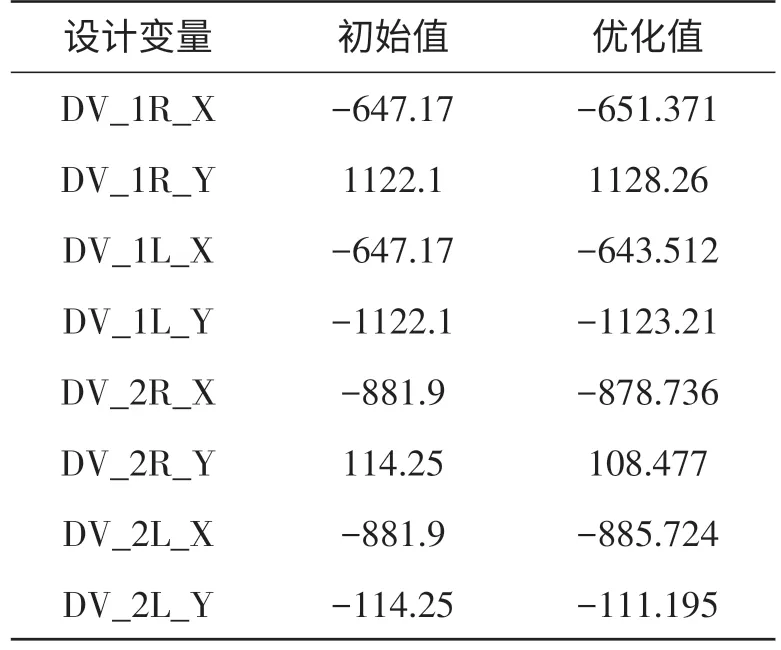
表4 设计变量最优值mm

5 结论

基于Adams/View模块建立了此重型汽车断开式转向系统的简化模型，进行运动学仿真分析，得到模型内外轮实际转角，将实际内外轮转角关系与理论值进行对比，存在较大误差，则对模型进行优化，对比优化前后的曲线图可知，优化前在内轮转角较大时误差值较大，严重影响转向系统的转角轨迹，优化后误差值明显减小，当内轮转角为38°时，外轮实际转角由优化前24.44°变为优化后26.7885°，误差由10.96%降为2.06%，更接近理论转角值，优化结果比较理想，从而改善该汽车转向系统操纵稳定性和平顺性。

[1]曾红，张志华，李铁军.基于ADAMS的横置液压缸式叉车转向系统的优化设计[J].机床与液压，2009，37（6）：179-182.

[2]黄伟.基于ADAMS的重卡双前桥转向仿真与优化[J].安徽农学通报，2007，13（9）：39-40.

[3]陈朝阳，陈娜，张代胜.基于灵敏度分析的双前桥转向系统摇臂机构的优化[J].合肥工业大学学报，2010，33（6）：801-807.

[4]储胜林.基于ADAMS的某车型转向特性分析[J].汽车实用技术，2014（5）：40-43.

[5]朱林，冯樱，严运兵.基于响应面法的双前桥转向机构参数优化[J].湖北汽车工业学院学报，2013,27（1）：1-4+11.

[6]廖小亮，孙泽海.基于ADAMS的FSAE赛车转向梯形机构的优化设计[J].湖北汽车工业学院学报，2011（4）：39-42.