基于Voronoi图的蜂群优化算法在WSN覆盖中的应用*

穆天圆，乔学工*，张 敏

（太原理工大学信息工程学院，太原030024）

基于Voronoi图的蜂群优化算法在WSN覆盖中的应用*

穆天圆1，乔学工1*，张 敏2

（太原理工大学信息工程学院，太原030024）

包含移动节点的混合网络成为无线传感器网络发展的主流。为了优化混合无线传感器网络的部署质量，提高部署效率，提出一种基于Voronoi图的蜂群优化算法来指导移动节点的部署。通过Voronoi多边形迅速找到固定节点部署的覆盖漏洞，指导引领蜂的生成，利于迅速定位全区域覆盖漏洞；通过评价漏洞大小代替轮盘赌选择方式来实现跟随蜂的开采过程，利于局部优化。仿真结果表明，该算法简便易实现，能够迅速收敛，提高网络覆盖率，达到混合网络的最优覆盖效果。

无线传感器网络；网络覆盖优化；人工蜂群算法；Voronoi多边形

无线传感器网络（WSN）综合了网络技术、信号处理技术、应用技术、现代网络及无线通信技术，在国防、工业、交通等领域中得到了广泛应用［1］。

构建无线传感器网络首先要考虑网络节点的部署及网络覆盖问题。由具有感知、计算、通信功能的大量固定节点和少量移动节点组成的混合无线传感器网络可以通过移动节点的位置调整，实现目标区域的优质覆盖，具有良好的环境适应能力，日益受到人们的关注［2］。因此，本文就随机部署情况下混合无线传感器网络移动节点的优化部署问题进行了研究。文献［3］使用改进的粒子群算法指导无线传感器网络的部署，在一定程度上提高了网络覆盖率，但算法容易陷入局部最优解。文献［4］提出了带精英策略的非支配排序遗传算法的网络覆盖方案，获得了较好的网络覆盖率，但算法复杂度过大。文献［5-6］使用人工蜂群（artificial bee colony，ABC）算法指导网络布局，但算法收敛速度慢，容易陷入局部最优。近年来，计算几何学中的Voronoi图（即泰森多边形）在无线传感器网络的覆盖控制问题上得到了很好的应用。Lee等［7］提出了基于泰森多边形形心的部署策略（Centroid-Based scheme，CBS），一定程度上降低了算法复杂度，但网络覆盖效果不够理想。Han等［8］提出改进的CBS算法，结合虚拟力知识，提出形心导向虚拟力的节点自部署算法，但在算法实现过程中需要进行多次试验。

本文针对基本ABC算法的不足，引入Voronoi多边形寻找覆盖漏洞，用于改进蜂群算法，并把改进人工蜂群算法（Voronoi artificial bee colony，VABC）应用到WSN的覆盖优化问题中，从而实现传感器节点的动态优化部署。仿真实验表明：该算法克服了基本ABC算法收敛速度慢和“早熟”的缺点，极大的提高了网络覆盖率，确保了良好的网络服务质量。

1 相关问题描述

1.1 人工蜂群算法

人工蜂群算法是模拟蜜蜂采蜜行为的智能群算法，具有控制参数少，健壮性的优点［9］，可以解决连续、组合优化问题。在基本蜂群算法中，蜜源初始位置在搜索空间内随机产生；引领蜂和侦察蜂进行随机性的位置更新，对新蜜源的开采和探索具有很大的不确定性和偶然性；跟随蜂采用轮盘赌的方法选择引领蜂进行跟随搜索，这些随机性过程使算法很容易出现收敛速度慢、早熟等问题。

1.2 Voronoi多边形

Voronoi多边形是几何学中的重要结构，在很多领域都得到了广泛使用，它的一个重要应用是有效描述点与点之间的邻近关系。本文利用Voronoi多边形进行固定节点部署后的覆盖漏洞的查找及其大小的评价，具有很强的适用性。文中用d（·）表示括号中任意两点的欧氏距离，R表示节点覆盖圆的半径。

1.2.1 Voronoi多边形

设直线L（A，B）={Q∈S|d（A，Q）=d（B，Q）}为线段AB的垂直平分线，则L（A，B）将平面S分成两个半平面。半平面area（A，B）表示S中更加靠近A点的区域：

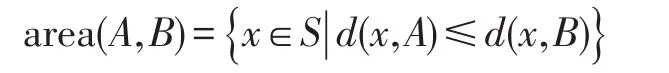
称为点A关于B的支配区域。可得到S区域中以A点为中心的对应Voronoi多边形区域：

式中：Q表示S区域中所有节点的集合。

1.2.2 区域覆盖漏洞

在监测区域内，对比各传感器节点到它对应的Voronoi多边形的所有顶点的距离与本节点覆盖圆半径的大小，可以判断是否有覆盖漏洞的存在。Voronoi多边形各顶点到传感器的距离用d（A，v）表示，其中A表示传感器节点，v表示任一Voronoi顶点，则

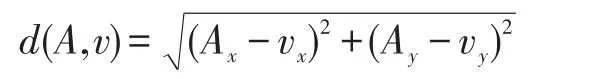
用R表示传感器的感知半径，如果d（A，v）＞R，则说明节点A所在的Voronoi多边形区域出现覆盖漏洞。

1.2.3 寻找漏洞实例

将随机分布的节点划分Voronoi多边形后，根据Voronoi多边形内部的点距离相应节点最近的原理，通过比较Voronoi多边形的顶点与对应节点覆盖区域的位置关系可以确定是否有覆盖漏洞的存在。如果Voronoi多边形的顶点未被覆盖，则出现覆盖漏洞，该顶点即被定义为覆盖漏洞顶点。

图1为随机分布的40个传感器节点对应的网络覆盖图，其中“·”表示传感器节点，“○”表示节点对应的覆盖区域，“-”表示Voronoi多边形的边，“▲”表示覆盖漏洞顶点。

图1 Voronoi多边形寻找覆盖漏洞

1.3 区域覆盖率

1.3.1 覆盖模型

假设Si为区域S中任意一点，A为区域中的任意传感器节点，Si与节点A的距离为d（A，Si）。在布尔模型中，节点A对目标点Si的检测概率由下式（1）得到：

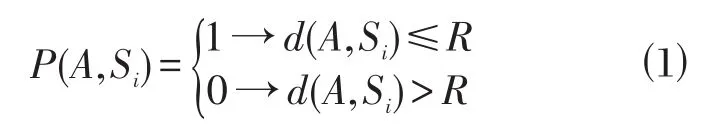
将区域S离散化为m×n个网格点，则区域S中有效覆盖的网格点数count为

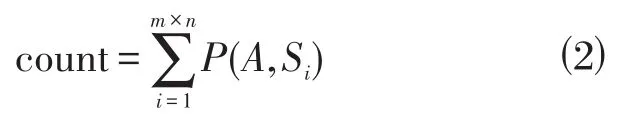
1.3.2 覆盖率Cov

覆盖率Cov是指目标监测区域中能够被部署的传感器节点所覆盖的面积与监测区域总面积的比值，是评价无线传感器网络覆盖质量的重要指标，是研究的热点［10］。覆盖率的好坏除与节点自身的感知能力有关外，节点的部署位置也很大程度上影响覆盖率的大小。本文将区域S离散化为m×n个网格点，每个网格点是否被覆盖用式（1）衡量，则覆盖率Cov简化为有效覆盖的网格点数count与总点数m×n的比值，即

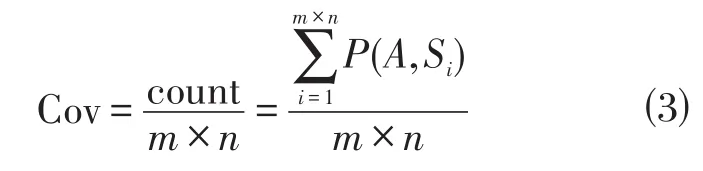
2 基于VABC的覆盖优化策略

从蜂群算法的基本原理可知：算法中每个食物源对应一个移动节点的位置，搜索最优食物源即寻找移动节点最优部署位置的过程。移动节点的个数等于引领蜂的个数，同时也等于跟随蜂的个数。

2.1 引领蜂的产生

传统ABC算法中，随机产生新的蜜源，引领蜂的搜索过程也是随机行为。VABC算法则首先根据节点的随机部署情况，生成固定节点相对应的Vor⁃onoi多边形，利用Voronoi顶点找出固定节点的覆盖漏洞，从覆盖漏洞中选择产生新蜜源，并指导引领蜂的搜索过程，迅速定位蜜源在整个目标区域的大概位置，计算蜜源的适应度值，根据贪婪算法选择确定保留的蜜源，有利于全局寻优，迅速收敛。

2.2 跟随蜂选择策略的改进

在基本人工蜂群算法中，跟随蜂采用轮盘赌的方法选择引领蜂，具有很大的随机性，容易陷入局部极值。而VABC算法通过评价覆盖漏洞的大小来分配跟随蜂。跟随蜂在覆盖漏洞顶点附近进行局部调整，并计算蜜源的适应度值，根据贪婪算法选择确定保留的蜜源，有利于局部最优值的寻找。

目标区域经Voronoi划分后覆盖漏洞的评价策略如下：

如图2为传感器节点A生成的Voronoi多边形，连接节点A和Voronoi多边形的顶点，将多边形分为以A点和一条Voronoi边（以M和N为顶点）构成的不同的Voronoi三角形区域。根据节点A的覆盖圆与Voronoi多边形顶点的相对位置关系，可以计算评价覆盖漏洞area（AMN）的大小［11］。

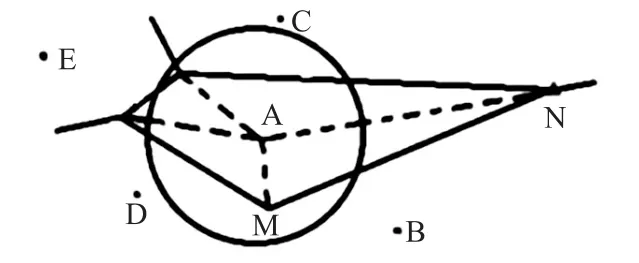
图2 节点A生成的Voronoi多边形

①当节点A的覆盖圆将顶点M和N完全覆盖在内，即距离比较公式d（A，M）≤R和d（A，N）≤R都成立时，则不存在覆盖漏洞；

②顶点M，N中的一个落在节点A的覆盖圆内，不妨设点M落在覆盖圆内，即d（A，M）≤R，而d（A，N）＞R。显然这种情况下△AMN不能被节点A的覆盖圆完全覆盖，必然出现覆盖漏洞。过A点作边MN的垂线，设垂足为P。利用余弦公式可求出∠AMN的值：

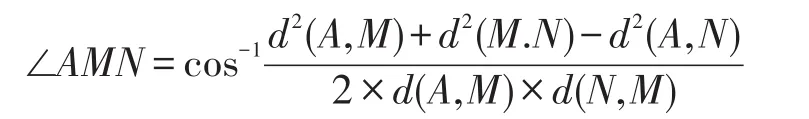
根据∠AMN是否为钝角判断垂足P是否落在线段MN内部，分两种情况计算漏洞面积，如图3所示。

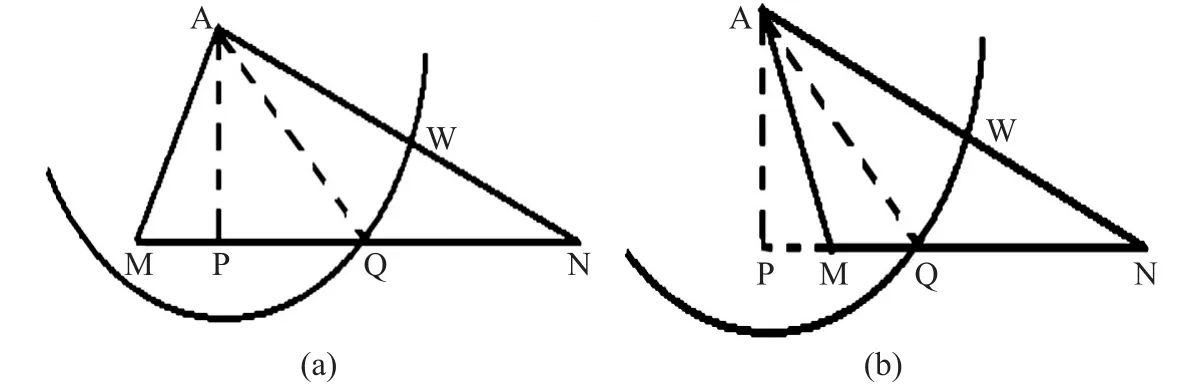
图3 覆盖漏洞判断

（a）垂足P落在线段MN内部，则∠AMN≤∏/2，如图3（a）所示：

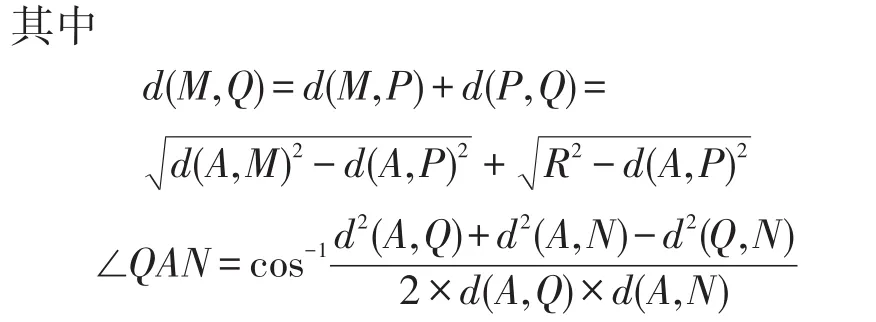
（b）垂足P落在线段MN外部，则∠AMN＞∏/2，如图3（b）所示，△AMN内存在的覆盖漏洞面积的计算与垂足落在线段MN内原理相同，只是各个小区域面积计算略有不同。可得三角形△AMN内存在的覆盖漏洞面积为

area(AMN)=area(ΔAMN)-area(ΔAMQ)-area(QAW)

③顶点M，N都在节点A的覆盖圆外，即距离比较公式d（A，M）＞R和d（A，N）＞R都成立，根据Vor⁃onoi三角形的形状和相对节点覆盖圆的位置分四种情况进行讨论，其覆盖漏洞面积计算原理与上文中有一个顶点落在覆盖圆内相同，此处不再赘述。

2.3 最差蜜源的替换

在ABC算法迭代过程中，下一代引领蜂和跟随蜂可能依据本代的最差蜜源产生新蜜源，但最差蜜源不利于获得最优结果，这在一定程度上影响了算法的收敛速度。在VABC算法中，通过Voronoi多边形产生的蜜源会出现面积很小的覆盖漏洞，这类漏洞在WSN网络的联通范围内是允许存在的，并不影响网络的正常运行，如图4中的A点所示。

图4 最差蜜源实例

这类覆盖漏洞即被视为最差蜜源。当搜索得到最差蜜源时，相应的引领蜂转变为侦查蜂，放弃原有最差蜜源，重新搜索，产生新蜜源来继续算法的循环执行。

2.4 算法执行

蜂群按照基于Voronoi图的蜂群优化算法进行搜索，根据蜂群的适应度值大小进行贪婪选择优化，重复上面的过程直到满足终止条件。

算法的具体步骤描述如下：①随机部署网络节点，利用公式（3）计算网络初始覆盖率。根据固定节点部署情况生成对应的Voronoi多边形，并找出覆盖漏洞顶点；②初始化种群规模、引领蜂数量、最大轮数等参数；③随机选取漏洞顶点作为移动节点初始位置，分配引领蜂，并进行全局搜索，根据公式（3）评价网络覆盖率，由贪婪法则选择其中较好的解来更新移动节点位置，有利于迅速找到全局最优解；④对步骤（c）进行有限次循环后，若发现存在未提高网络覆盖率的移动节点位置，则相应的引领蜂转变为侦查蜂进行搜索，产生新的移动节点位置取代原来的节点位置；⑤评价覆盖漏洞大小，选取较大漏洞分配跟随蜂，跟随蜂进行细致的局部搜索，根据公式（3）评价网络覆盖率，由贪婪法则选择其中较好的解来更新移动节点位置，利于局部最优解的寻找；⑥判断是否达到最大循环次数，如果达到最大执行轮数，则停止循环，否则根据网络覆盖率对新的蜂群再一次进行搜索，即转到步骤（c）继续搜索；⑦记录最优的移动节点位置作为寻优结果，生成最终的网络覆盖图。

算法流程图如下图5。

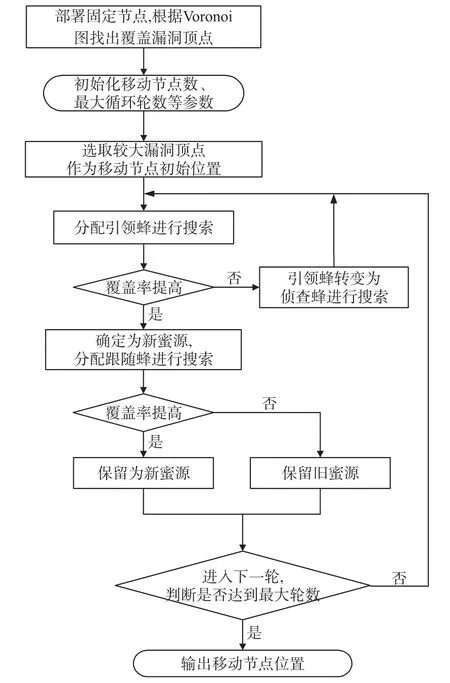
图5 算法流程图

3 仿真实验分析

假设无线传感器网络监测区域为100 m×100 m的正方形，在这个区域内随机放置30个传感器固定节点，20个传感器移动节点，每个传感器节点的感知距离为10 m，通信距离为20 m。ABC算法和VABC算法参数为：种群规模50，雇佣蜂数20，食物源数20，最大迭代次数1 000。

图6（a）是节点随机部署的情况，黄色表示固定节点，蓝色表示移动节点，生成固定节点的Voronoi多边形，寻找到固定节点部署漏洞，网络初始覆盖率为72.82%；图6（b）是使用VABC算法优化后的节点位置，移动节点很好的填补了覆盖漏洞，网络覆盖率达到95.42%，移动节点覆盖均匀，达到了很好的覆盖效果。

为了进一步验证VABC覆盖优化策略的性能，将本文算法与文献［12］中提出的混沌人工蜂群算法CABC进行比较。图7是使用ABC算法、CABC算法和VABC算法优化后区域的覆盖率提升曲线对比图，可以看出CABC算法能够较快收敛，达到算法的最大覆盖率，最终区域覆盖率稳定在93.48%；ABC算法的最终区域覆盖率可达到90.81%，但它的收敛速度慢，需要运行一段时间才能稳定；VABC覆盖优化策略运行20轮后迅速提升网络覆盖率到90.12%，这是由于Voronoi多边形漏洞顶点指导算法迅速定位全局漏洞，提高收敛速度；通过调整移动节点与覆盖漏洞的相对位置，最终优化网络覆盖率达到95.42%，明显优于CABC算法和基本ABC算法，提高了网络覆盖率，具有很好的覆盖效果。

本文中定义覆盖率达到本算法最大覆盖率的97%所需执行的轮数来评价算法的收敛速度。表1通过不同算法的相关数据比较来直观反映基本ABC算法、混沌人工蜂群算法和Voronoi人工蜂群算法的性能优劣。

图7 不同算法收敛速度比较

表1 不同算法的数据比较

4 结束语

本文将几何学中的Voronoi多边形理论与蜂群算法相结合，提出VABC算法并应用于无线传感器网络的移动节点部署。通过仿真实验对VABC算法进行分析，实验结果表明：该算法结构简单，能很好的避免基本ABC算法收敛速度慢，易陷入局部极值的缺点，具有很好的实用效果。

［1］李岳衡，王慧斌.无线传感器网络与监测应用［M］.北京：国防工业出版社，2011：7-11.

［2］徐凌伟，张浩，Gulliver T A，等.移动无线传感器网络系统在n-Rayleigh信道下的性能分析［J］.传感技术学报，2015（2）：265-270.

［3］Penny J S，David J B，Steven B，et al.A Study to Evaluate a Low Cost Virtual Reality System for Home-Based Rehabilitation of the Up-Per Limb Following Stroke［J］.International Journal on Dis⁃ability and Human Development，2011，10（4）：337-341.

［4］Stone E E，Skubic M.Evaluation of an Inexpensive Depth Camera for Passive In-Home Fall Risk Assessment［C］∥2011 5th Interna⁃tional Conference on Pervasive Computing Technologies for Healthcare（Pervasive Health 2011），2011：71-77.

［5］胡珂.基于人工蜂群算法在无线传感网络覆盖优化策略中的应用研究［D］.成都：电子科技大学，2012.

［6］0zturk C，Karaboga D，Gorkemli B.Probabilistic Dynamic Deploy⁃ment of Wireless Sensor Networks by Artificial Bee Colony Algo⁃rithm［J］.Sensors，2011，11（6）：6056-6065.

［7］Lee H J，Kim Y H，Han Y H，et al.2009 Proceedings of the IEEE 70th Vehicular Technology Conference Fall（VTC 2009-Fall）An⁃chorage，AK，September 20-23，2009 p1.

［8］Han Y H，Kim Y H，Kim W，et al.2011 Simulation 88 1152.

［9］Karaboga D，Bpasturk B.On the Performance of Artificial Bee Col⁃ony（ABC）Algorithm［J］.Applied S0ft Comuting，2008，8（1）：687-697.

［10］秦宁宁，陈家乐，丁志国.覆盖率均衡区域覆盖算法［J］.传感技术学报，2015（4）：578-584.

［11］周则顺.无线传感器网络覆盖与连通优化算法的研究［D］.武汉：武汉理工大学，2013.

［12］文政颖，翟红生.基于混沌人工蜂群算法的无线传感器网络覆盖优化［J］.计算机测量与控制，2014，22（5）：1609-1612.

穆天圆（1990-），男，硕士研究生，主要研究方向为无线传感器网络节点部署及覆盖，972130219@qq.com；

乔学工（1968-），女，副教授，硕士生导师，主要研究方向为无线传感器网络，qiaoxg1968@aliyun.com；

张 敏（1990-），男，硕士研究生，主要研究方向为无线传感器网络定位，1259104763@qq.com。

The Application of Bee Colony Optimization Algorithms Based on Voronoi in the Coverage of Wireless Sensor Networks*

MU Tianyuan1，QIAO Xuegong1*，ZHANG Min2
（College of Information Engineering，Taiyuan University of Technology，Taiyuan 030024，China）

The hybrid network which is composed of fix and mobile nodes has become the mainstream in the devel⁃opment of wireless sensor networks（WSNs）.In order to optimize the deployable quality of the mixed wireless sensor network，and improve the efficiency of deployment，a Bee Colony Algorithm optimized with Voronoi was proposed to guide the deployment of mobile nodes.The covering loopholes of the fixed nodes can be quickly found by the algo⁃rithm through the Voronoi polygons，which guide the development of the leading bees.It is conducive to quickly lo⁃cating all the covering loopholes in the target area.Instead of roulette algorithm method，evaluating the size of gap⁃ing holes by following bees’exploiting process is conductive to local optimization.The simulation results show that the algorithm is simple to implement，converges rapidly，improves the coverage ratio of the network and achieves the optimal coverage of the network.

wireless sensor networks（WSNs）；coverage optimization；artificial bee colony algorithm；Voronoi polygon

TP393

A

1004-1699（2015）10-1525-06

��6150P

10.3969/j.issn.1004-1699.2015.10.019

项目来源：国家自然科学基金项目（51279122）；山西省自然科学基金项目（2012011013-5）；山西省软科学基金项目（2014041048-4）

2015-04-12 修改日期：2015-07-25